AcWing 854. Floyd求最短路Floyd模板
Floyd算法:
标准弗洛伊德算法,三重循环,基于动态规划。
循环结束之后 d[i][j]存储的就是点 i 到点 j 的最短距离。
需要注意循环顺序不能变:第一层枚举中间点,第二层和第三层枚举起点和终点。
特点:
1.复杂度为O(n^3),只能处理200以内的点。
2.一次求出所有结点直接的最短路径。
3.能处理有负权边的图。
Floyd模板:
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=205;
int n,m,d[N][N];
int main(){scanf("%d%d%d",&n,&m);//初始化 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)d[i][j]=i==j?0:INF; //自己到自己的距离为0 //输入边 for(int i=0,x,y,w;i<m;i++){scanf("%d%d%d",&x,&y,&x);d[x][y]=d[y][x]=min(d[x][y],w);}//Floyd核心代码 for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){
// if(d[i][k]==INF||d[k][j]==INF) continue; //防止负权影响INF if(d[i][j]>d[i][k]+d[k][j])d[i][j]=d[i][k]+d[k][j];
// e[i][j]=min(e[i][j],e[i][k]+e[k][j]); //数据量大时,min会慢一些 }}}cout<<d[1][n];return 0;
} AcWing 854. Floyd求最短路
给定一个 nn 个点 mm 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 kk 个询问,每个询问包含两个整数 xx 和 yy,表示查询从点 xx 到点 yy 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,kn,m,k。
接下来 mm 行,每行包含三个整数 x,y,zx,y,z,表示存在一条从点 xx 到点 yy 的有向边,边长为 zz。
接下来 kk 行,每行包含两个整数 x,yx,y,表示询问点 xx 到点 yy 的最短距离。
输出格式
共 kk 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出
impossible。
数据范围
1≤n≤200 1≤n≤200,
1≤k≤n2 1≤k≤n2
1≤m≤20000 1≤m≤20000,
图中涉及边长绝对值均不超过 1000010000。
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1代码:
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=205;
int n,m,k,x,y,z,e[N][N];
int main(){scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=n;i++) //初始化 for(int j=1;j<=n;j++)e[i][j]=i==j?0:INF;for(int i=0;i<m;i++){scanf("%d%d%d",&x,&y,&z);e[x][y]=min(e[x][y],z);}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(e[i][k]==INF||e[k][j]==INF) continue; //防止负权影响INF,或者在输出的时候判断e[x][y]>INF/2 if(e[i][j]>e[i][k]+e[k][j])e[i][j]=e[i][k]+e[k][j];
// e[i][j]=min(e[i][j],e[i][k]+e[k][j]); //数据量大时,min会慢一些 }}}while(k--){scanf("%d%d",&x,&y);if(e[x][y]==INF) cout<<"impossible"<<endl; //存在负权时,如果不存在通路,不一定是INF,会小一些 else cout<<e[x][y]<<endl;}return 0;
} 相关文章:

AcWing 854. Floyd求最短路Floyd模板
Floyd算法: 标准弗洛伊德算法,三重循环,基于动态规划。 循环结束之后 d[i][j]存储的就是点 i 到点 j 的最短距离。 需要注意循环顺序不能变:第一层枚举中间点,第二层和第三层枚举起点和终点。 特点: 1.复杂…...
Graph Theory(图论)
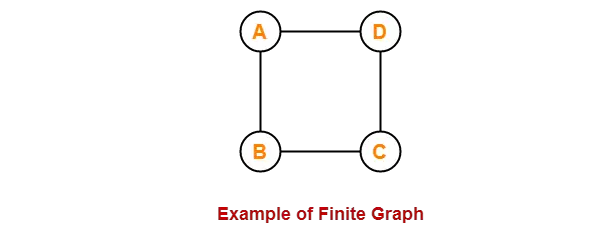
一、图的定义 图是通过一组边相互连接的顶点的集合。 In this graph, V { A , B , C , D , E } E { AB , AC , BD , CD , DE } 二、图的类型 2.1 Finite Graph A graph consisting of finite number of vertices and edges is called as a finite graph. Null Graph Tri…...

[Python]生成 txt 文件
前段时间有位客户问: 你们的程序能不能给我们生成个 txt 文件,把新增的员工都放进来,字段也不需要太多,就要 员工姓名/卡号/员工编号/员工职位/公司 这些字段就行了,然后我们的程序会去读取这个 txt 文件,拿里面的内容,读完之后会这个文件删掉 我: 可以接受延迟吗?可能没办法实…...

GeoTools实战指南: 自定义矢量样式并生成截图
GeoTools实战指南: 自定义矢量样式并生成截图 介绍 本段代码的主要功能是将矢量数据(Shapefile)渲染成一张图片。 准备环境 首先,您需要将GeoTools库添加到您的项目中。使用Maven或Gradle添加依赖项,或者直接下载GeoTools的jar文件并添加到您的类路径中。 Maven <…...

深度学习超参数调整介绍
文章目录 深度学习超参数调整介绍1. 学习率2. 批大小3. 迭代次数4. 正则化5. 网络结构总结 深度学习超参数调整介绍 深度学习模型的性能很大程度上取决于超参数的选择。超参数是指在训练过程中需要手动设置的参数,例如学习率、批大小、迭代次数、网络结构等等。选择…...
Bootloader
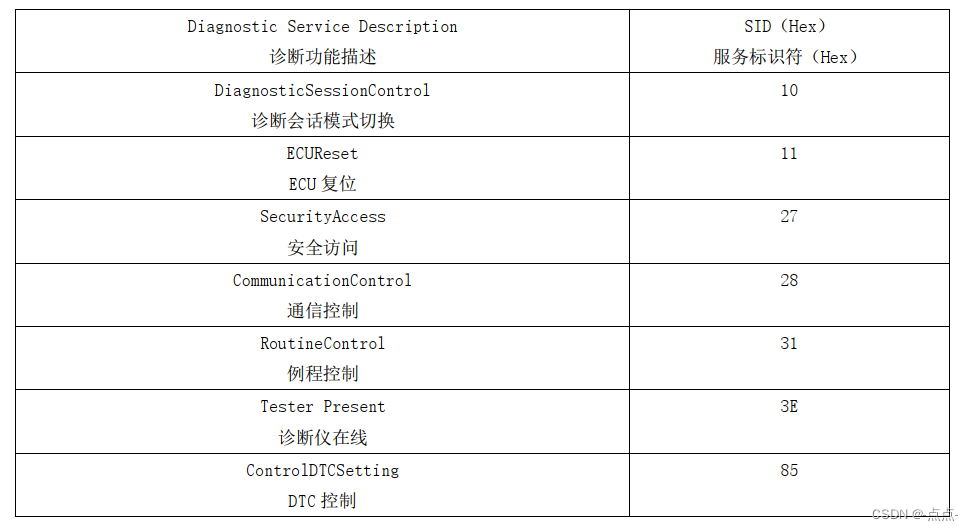
本篇不作太过的技术了解,仅可作为初学者的参考。用嘴简单的语言讲清楚一件事。 项目中遇到Bootloader升级MCU,我很好这是什么软件,逻辑是什么,怎么升级的。 术语及定义 指纹信息fingerprint诊断仪用于标识特定的下载尝试的信息 …...

安卓开发_广播机制_广播的最佳实践:实现强制下线功能
安卓开发_广播机制_广播的最佳实践:实现强制下线功能 ActivityCollector类用于管理所有的ActivityBaseActivity类作为所有Activity的父类创建一个LoginActivity来作为登录界面布局LoginActivity 在MainActivity中加入强制下线功能布局MainActivity在BaseActivity中注…...
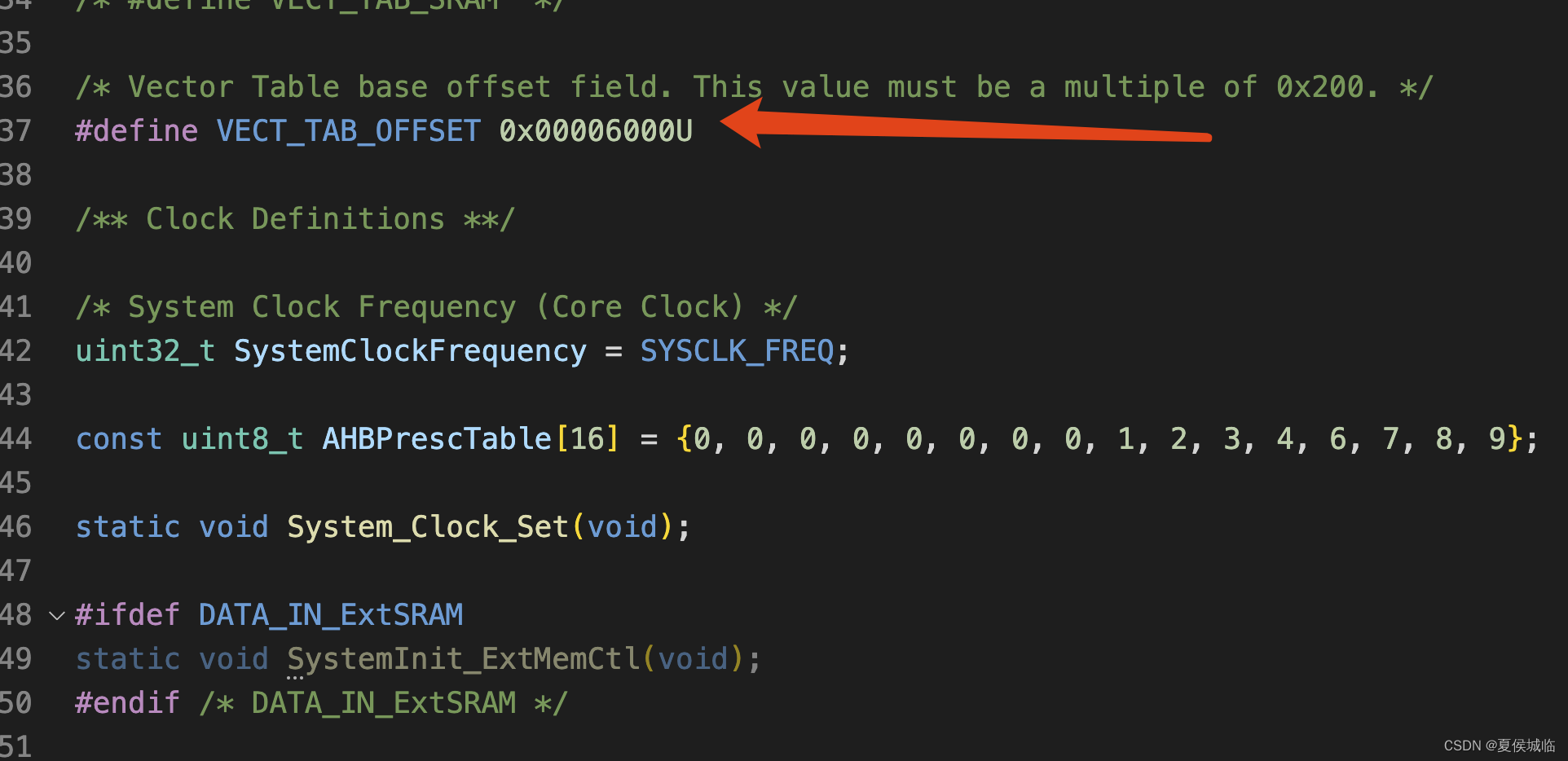
国民技术N32G430开发笔记(10)- IAP升级 Application 的制作
IAP升级 Application 的制作 1、App程序跟Bootloader程序最大的区别就是, 程序的执行地址变成了之前flash设定的0x08006000处, 大小限制为20KB 所以修改Application工程的ld文件 origin 改成 0x08006000 length 改成0x5000 烧录是起始地址也要改为x0x…...

[计算机图形学]材质与外观(前瞻预习/复习回顾)
一、图形学中的材质 不同的物体表面有着不同的材质,而不同的材质意味着它们与光线的作用不同。那么我们之前在介绍辐射度量学和渲染方程提到过其中一个函数,叫做BRDF,而在实际上,也就是BRDF定义了不同的材质。BRDF决定了光如何被反…...
Java 的简要介绍及开发环境的搭建(超级详细)
图片来源于互联网 目录 | CONTENT Java 简介 一、什么是 Java 二、认识 Java 版本 三、选择哪个版本比较好 搭建 Java 开发环境 一、下载 Java 软件开发工具包 JDK 二、配置环境变量 自动配置 手动配置 三、下载合适的 IDE IntelliJ IDEA Visual Studio Code Eclip…...

每天一道算法练习题--Day15 第一章 --算法专题 --- -----------二叉树的遍历
概述 二叉树作为一个基础的数据结构,遍历算法作为一个基础的算法,两者结合当然是经典的组合了。很多题目都会有 ta 的身影,有直接问二叉树的遍历的,有间接问的。比如要你找到树中满足条件的节点,就是间接考察树的遍历…...

golang - 函数的使用
核心化编程 为什么需要函数? 代码冗余问题不利于代码维护函数可以解决这个问题 函数 函数:为完成某一功能的程序指令(语句)的集合,称为函数 在 Go 中,函数分为:自定义函数(自己写…...

真题详解(极限编程)-软件设计(六十一)
真题详解(二分查找平均值)-软件设计(六十)https://blog.csdn.net/ke1ying/article/details/130417464 VLANtag属于 数据链路层实现。 数据链路层:网桥交换机。 网络层:路由器。 物理层:中继器。 Telent…...

计算机网络笔记:TCP粘包
默认情况下, TCP 连接会启⽤延迟传送算法 (Nagle 算法), 在数据发送之前缓存他们. 如果短时间有多个数据发送, 会缓冲到⼀起作⼀次发送 , 这样可以减少 IO 消耗提⾼性能。 如果是传输⽂件的话, 那么根本不⽤处理粘包的问题, 来⼀个包拼⼀个包就好了。但是如果是多条消息, 或者…...

Vue(标签属性:ref、配置项:props、混入mixin、插件、样式属性:scroped)
一、ref(打标识) 前面提及到了标签属性:keys 这里将了解ref:打标识 正常布置脚手架并创建入口文件main.js,引入组件 1. 可以给元素注册引用信息(获取真实DOM) 给一个按钮获取上方的dom的方法,方…...
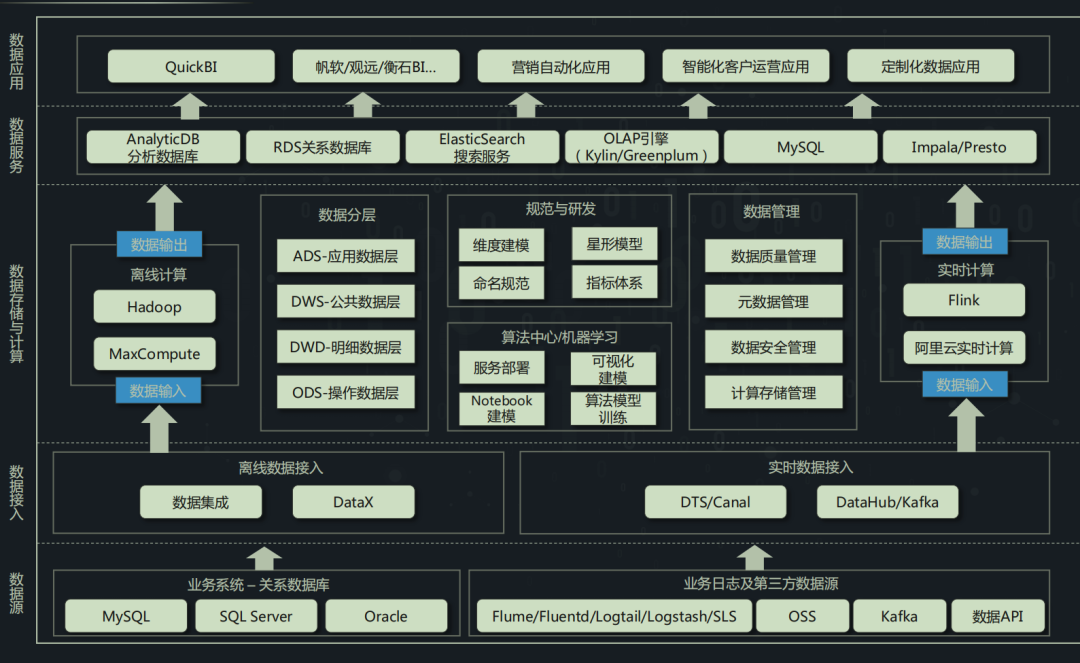
数仓建设规划核心问题!
小A进入一家网约车出现服务公司,负责公司数仓建设,试用期主要一项 OKR是制定数据仓库建设规划;因此小 A 本着从问题出发为原点,先对公司数仓现状进行一轮深入了解,理清存在问题,然后在以不忘初心原则提出解…...

容器镜像的导入导出
容器镜像的导入导出 第1关:导入导出容器 任务描述 本关任务是学习导入导出容器,要求学习者参照示例完成将busyboxContainer容器的文件系统保存为一个tar包,通过该tar包导入一个busybox:v1.0镜像。 相关知识 将 "容器的文件系统&…...

Java每日一练(20230502)
目录 1. 二叉搜索树的最近公共祖先 🌟🌟 2. 随机分组问题 🌟 3. K 个一组翻转链表 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练…...

JVM学习(九):堆
一、堆(Heap)的概述 一个JVM实例只存在一个堆内存,堆也是Java内存管理的核心区域。 Java堆区在JVM启动的时候即被创建,其空间大小也就确定了。是JVM管理的最大一块内存空间。同时,堆内存的大小是可以调节的。《Java虚拟…...
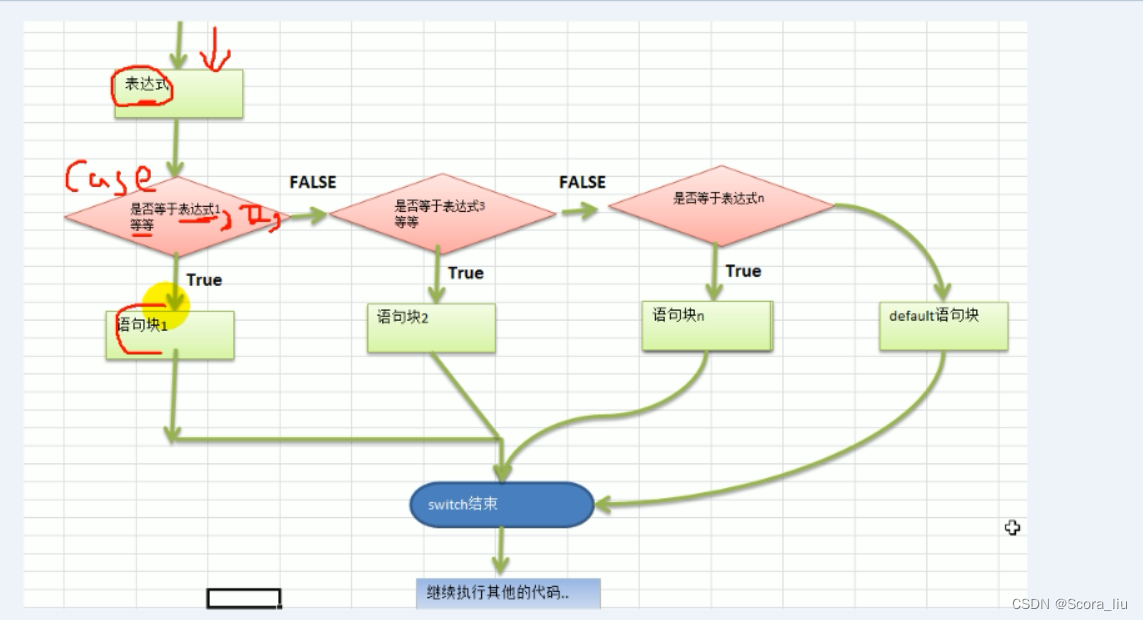
golang - switch
switch 的使用 switch 语句用于基于不同条件执行不同操作,,直每一个 case 分支都是唯一的,从上到下逐一测试到匹配为止匹配项后面也不需要再加 break switch 表达式 {case 表达式1, 表达式2, ... :语句块1case 表达式2, 表达式3, ... :语句块…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
