( 字符串) 9. 回文数 ——【Leetcode每日一题】
❓9. 回文数
难度:简单
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
- − 2 31 < = x < = 2 31 − 1 -2^{31} <= x <= 2^{31} - 1 −231<=x<=231−1
进阶: 你能不将整数转为字符串来解决这个问题吗?
💡思路:
法一:
- 转化为字符串
法二:进阶
- 反转一半数字
- 将整数分成左右两部分,右边那部分需要转置,然后判断这两部分是否相等。
🍁代码:(Java、C++)
法一:
Java
class Solution {public boolean isPalindrome(int x) {if(x < 0) return false;String s = String.valueOf(x);for(int i = 0, j = s.length() - 1; i < j; i++, j--){if(s.charAt(i) != s.charAt(j)) return false;}return true;}
}
C++
class Solution {
public:bool isPalindrome(int x) {if(x < 0) return false;string s = to_string(x);for(int i = 0, j = s.size() - 1; i < j; i++, j--){if(s[i] != s[j]) return false;}return true;}
};
法二:
Java
class Solution {public boolean isPalindrome(int x) {if(x == 0) return true;if(x < 0 || x % 10 == 0) return false;int y = x % 10;while(x > y){x /= 10;y = y * 10 + x % 10;}return x == y || x == y / 10;}
}
C++
class Solution {
public:bool isPalindrome(int x) {if(x == 0) return true;if(x < 0 || x % 10 == 0) return false;int y = x % 10;while(x > y){x /= 10;y = y * 10 + x % 10;}return x == y || x == y / 10;}
};
🚀 运行结果:
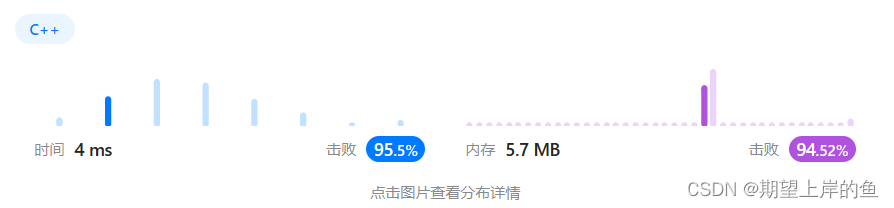
🕔 复杂度分析:
- 时间复杂度: O ( l o g n ) O(logn) O(logn),对于每次迭代,我们会将输入除以
10,因此时间复杂度为 O ( l o g n ) O(logn) O(logn)。 - 空间复杂度: O ( 1 ) O(1) O(1),我们只需要常数空间存放若干变量。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 字符串) 9. 回文数 ——【Leetcode每日一题】
❓9. 回文数 难度:简单 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如…...

SpringAOP
SpringAOP 一、AOP1. AOP简介1.1 AOP简介和作用1.2 AOP中的核心概念 2. AOP入门案例【重点】2.1 AOP入门案例思路分析2.2 AOP入门案例实现【第一步】导入aop相关坐标【第二步】定义dao接口与实现类【第三步】定义通知类,制作通知方法【第四步】定义切入点表达式、配…...
学系统集成项目管理工程师(中项)系列15_质量管理
1. 质量(Quality)的定义 1.1. 反应实体满足主体明确和隐含需求的能力的特性总和 1.2. 明确需求是指在标准、规范、图样、技术要求、合同和其他文件中用户明确提出的要求与需要 1.3. 隐含需求是指用户和社会通过市场调研对实体的期望以及公认的、不必明…...

统计学习方法第四章——朴素贝叶斯法
x.1 前言 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。是通过给定training dataset学习联合概率分布的方法,是一种生成方法。 x.2 使用贝叶斯定理做分类 使用贝叶斯定理做分类,相比较于朴素贝叶斯即丢除特征条件独立假设这个条件。 …...
安装配置goaccess实现可视化并实时监控nginx的访问日志
一、业务需求 我们安装了nginx后,需要对nginx的访问情况进行监控(希望能够实时查看到访问nginx的情况),如下图所示: 二、goaccess的安装配置步骤 2.1、准备内容 需要先安装配置nginx或OpenResty - 安装 Linux环境对Nginx开源版源码下载、编译、安装、开机自启https://b…...
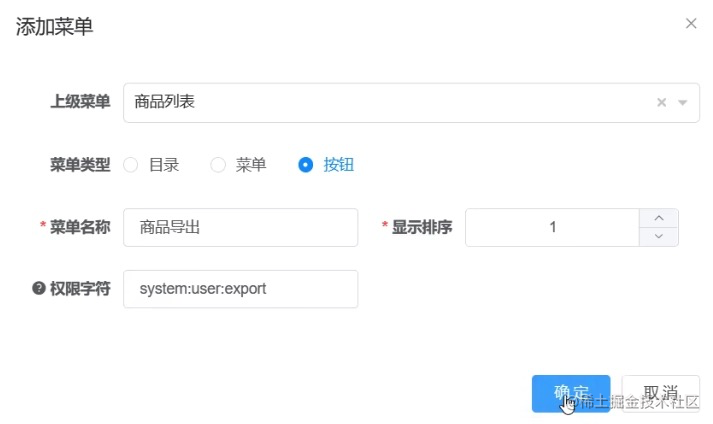
springboot第14集:MyBatis-CRUD讲解
注意点:增、删、改操作需要提交事务! 为了规范操作,在SQL的配置文件中,我们尽量将Parameter参数和resultType都写上! 编写Mapper接口类 import com.da.pojo.User; import java.util.List; public interface UserMapper…...

ES6新特性(1)
目录 一、字符串扩展 (1)字符串遍历器接口(for...of...) (2)模板字符串 二、字符串新增方法 (1)包含方法 (2)重复方法 (3)补全方…...
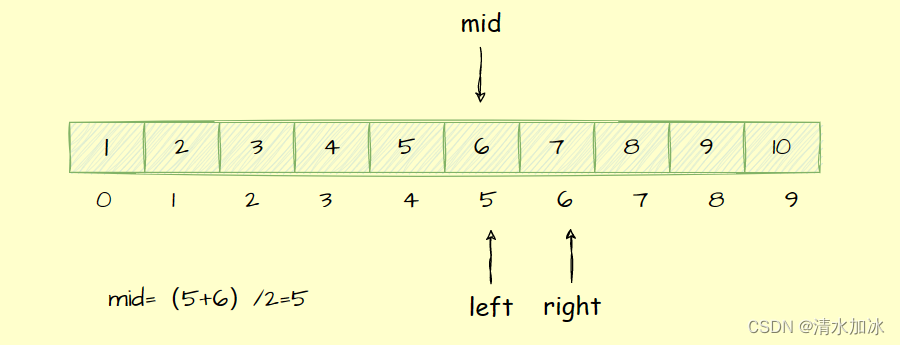
这就是二分查找?(C语言版)
大家好!我又来了,哈哈~今天我要和大家分享一种神奇的算法——二分查找!你可能会问,“二分查找有什么好玩的?”但在我看来它就像一场魔法表演,当你输入一个数,他会在一堆数中快速找到它的位置。找…...

操作系统之内存管理
连续分配 一、单一连续 直接为要运行的进程分配一个内存,只适合单任务,只能用于单对象、单任务,内存被分配为系统区和用户区,系统区在低地址,用户区是一个用户独享 二、等分分区 由于分配一个内存只能执行单任务&a…...
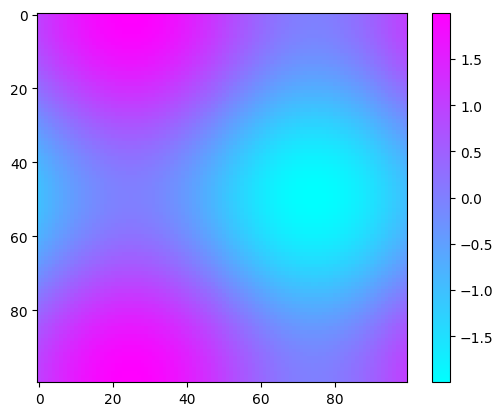
【Python | matplotlib】matplotlib.cm的理解以及举例说明
文章目录 一、模块介绍二、颜色举例 一、模块介绍 matplotlib.cm是Matplotlib中的一个模块,它提供了一组用于处理颜色映射(colormap)的函数和类。颜色映射是一种将数值映射到颜色的方法,常用于制作热力图、等值线图、散点图等。 …...
数据库单实例升级
一、单实例环境,全时长二个半钟多。详细图文说明到这下载 1、停止所有oracle相关进程。 Emctlstop dbconsole Isqlplusctl stop Lsnrctl stop sqlplus /nolog sql>conn /as sysdba Connectedtoanidleinstance. sql>shutdown 然后,冷备份下数据库cp…...

Photoshop如何使用选区之实例演示?
文章目录 0.引言1.利用快速选择工具抠图2.制作网店产品优惠券3.利用选区改变眼睛颜色4.抠取复杂的花束5.制作丁达尔光照效果6.利用选区调整图像局部颜色 0.引言 因科研等多场景需要进行绘图处理,笔者对PS进行了学习,本文通过《Photoshop2021入门教程》及…...

ThreadLocal的使用介绍和底层原理解析和开源框架的使用实例
文章目录 ThreadLocal的使用介绍和底层原理解析和开源框架的使用实例ThreadLocal简介ThreadLocal使用示例ThreadLocal原理解析Spring中ThreadLocal的应用小结ThreadLocal的使用步骤常见面试题案例解析(框架源码经典案例)案例实战 ThreadLocal的使用介绍和底层原理解析和开源框架…...

带你学c带你飞-P7取值范围
比特位 CPU能读懂的最小单元——比特位,bit,b 字节 内存机构的最小寻址单元——字节,Byte,B 1Byte8bit 进制 怎么算 注意:int默认是signed类型,signed类型第一位是符号位 符号位 存放signed类型的存…...

ramfs, rootfsinitramfs
什么是ramfs? ramfs是一个非常简单的文件系统,它将Linux的磁盘缓存机制(页面缓存和dentry缓存)导出为一个动态可调整大小的基于ram的文件系统。 Linux通常将所有文件缓存在内存中。从后备存储(通常是挂载文件系统的块设备)读取的数据页被保留下来,以防…...
)
十三届蓝桥杯研究生组国赛-最大公约数(线段树+二分)
十三届蓝桥杯研究生组国赛-最大公约数 1、问题描述2、解题思路2.1 解法一:暴力查询区间gcd(75%)2.2 解法二:线段树+二分法(AC)1、问题描述 问题描述 给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x,y x,y...

数据结构——二叉树层序遍历
数据结构——二叉树层序遍历 107. 二叉树的层序遍历 II199. 二叉树的右视图思路: 637. 二叉树的层平均值 107. 二叉树的层序遍历 II 107. 二叉树的层序遍历 II 给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节…...
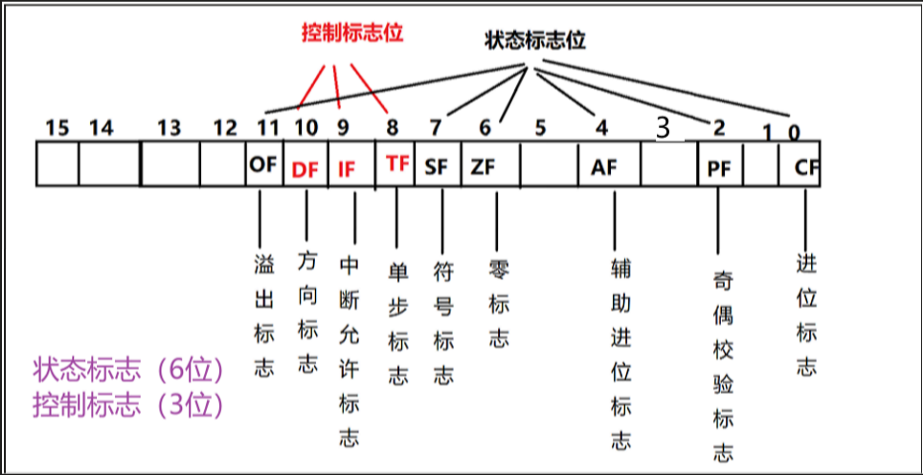
【微机原理】8088/8086微处理器
目录 一、8088/8086的功能结构 1.总线接口部件(BIU) 2.执行部件(EU) 二、8088/8086的寄存器结构(14个) 溢出标志的概念 溢出和进位的区别 8086CPU是Intel系列的16位微处理器,他有16根数据…...

springboot第12集:DAO功能代码
在Spring Boot中,DAO是数据访问对象的缩写,它是一种设计模式用于提供对数据库操作的抽象层。通过使用DAO模式,我们可以将数据操作与业务逻辑分离,并提供一个单独的接口来执行所有的数据库操作。 在Spring Boot中,通常使…...

基于KZG多项式承诺方案的RLN
1. 引言 RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自: Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting RLN(Rate-Limiting Nullifier)是一种…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
