P1050 [NOIP2005 普及组] 循环
题目描述
乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天,他突然对数的正整数次幂产生了兴趣。
众所周知,22 的正整数次幂最后一位数总是不断的在重复 2,4,8,6,2,4,8,6…2,4,8,6,2,4,8,6… 我们说 22 的正整数次幂最后一位的循环长度是 44(实际上 44 的倍数都可以说是循环长度,但我们只考虑最小的循环长度)。类似的,其余的数字的正整数次幂最后一位数也有类似的循环现象:
数字循环循环长度22,4,8,6433,9,7,1444,6255166177,9,3,1488,4,2,6499,12数字23456789循环2,4,8,63,9,7,14,6567,9,3,18,4,2,69,1循环长度44211442
这时乐乐的问题就出来了:是不是只有最后一位才有这样的循环呢?对于一个整数 �n 的正整数次幂来说,它的后k位是否会发生循环?如果循环的话,循环长度是多少呢?
注意:
- 如果 �n 的某个正整数次幂的位数不足 �k,那么不足的高位看做是 00。
- 如果循环长度是 �L,那么说明对于任意的正整数 �a,�n 的 �a 次幂和 �+�a+L 次幂的最后 �k 位都相同。
输入格式
共一行,包含 22 个整数 �n 和 �k。�n 和 �k 之间用一个空格隔开,表示要求 �n 的正整数次幂的最后 �k 位的循环长度。
输出格式
一个整数,表示循环长度。如果循环不存在,输出 −1−1。
输入输出样例
输入 #1复制
32 2
输出 #1复制
4
说明/提示
【数据范围】
对于 30%30% 的数据,满足 �≤4k≤4;
对于100%100% 的数据,满足 1≤�<101001≤n<10100,1≤�≤1001≤k≤100。
【题目来源】
NOIP 2005 普及组第四题
题意
给定两整数 �,�n,k,求 �n 的正整数次幂的最后 �k 位的循环长度,若循环不存在输出 −1−1。
1≤�≤10100,1≤�≤1001≤n≤10100,1≤k≤100
题解
这篇题解是对最高赞题解的补充与说明
在看最高赞题解的时候,因为没有放上计算过程,我对着题解手玩了好久才弄明白,所以就有了这篇附上计算过程的题解。
手玩数据 198123 4,因为要求只取后 4 位,所以将其截取成 8123。
我们逐位进行处理:
- 先处理最后一位的循环节:最后一位是
3,循环节长度为 4。所以后两位的循环节长度一定为 4 的倍数,为了加快计算,我们可以将乘数变为8123^4,取后 4 位变成0641。 - 再处理后两位:后两位是
23,在乘了 5 次0641后出现了循环,循环节长度为 4*5=20。同样为了加快计算,乘数变为8123^20=0641^5,取后 4 位变成9201。之后就按照这样的方法处理即可。 - 后三位:后三位是
123,乘了 5 次9201后出现循环,循环节长度为 20*5=100 ,乘数变为9201^5%(10^4)=6001 - 后四位:后四位是
8123,乘了 5 次6001后出现循环,循环节长度为 100*5=500,500 就是最终的答案。
记得判断无解的情况:如果在处理某一位时,乘了乘数 10 次,还是没有出现循环,无解。
8123 1
8123*8123=65983129 2
3129*8123=25416867 3
6867*8123=55780641 4
0641*8123=05206843 #
8123^4=43537733126306418123 1
8123*0641=05206843 2
6843*0641=04386363 3
6363*0641=04078683 4
8683*0641=05565803 5
5803*0641=03719723 #
0641^5=1082156687392018123 1
8123*9201=74739723 2
9723*9201=89461323 3
1323*9201=12172923 4
2923*9201=26894523 5
4523*9201=41616123 #
9201^5=659439797557264460018123 1
8123*6001=48746123 2
6123*6001=36744123 3
4123*6001=24742123 4
2123*6001=12740123 5
0123*6001=00738123 #ans=4*5*5*5=500
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int k;
char str[205];
struct bignum
{int x[205];bignum(){memset(x,0,sizeof(x));}
}n,tmp,mul,ans;
bignum operator *(bignum a,bignum b)//特化过的高精乘 只取后k位
{bignum ans;for(int i=0;i<k;i++)for(int j=0;j<k;j++)ans.x[i+j]+=a.x[i]*b.x[j];for(int i=0;i<k;i++)ans.x[i+1]+=ans.x[i]/10,ans.x[i]%=10;for(int i=k;i<205;i++)ans.x[i]=0;return ans;
}
bignum operator *(bignum a,int b)//这个高精乘低精是ans专用的233
{for(int i=0;i<=200;i++)a.x[i]*=b;for(int i=0;i<=200;i++)a.x[i+1]+=a.x[i]/10,a.x[i]%=10;return a;
}
int main()
{scanf("%s %d",str,&k);ans.x[0]=1;int len=strlen(str);for(int i=0;i<k;i++)n.x[i]=str[len-i-1]-'0';mul=n;for(int i=0;i<k;i++){bignum tmp=n;int j=1,flag=1;for(j=1;j<=10;j++){tmp=tmp*mul;if(tmp.x[i]==n.x[i]){ans=ans*j;flag=0;break;}}if(flag)return puts("-1"),0;tmp=mul;for(int k=1;k<j;k++)mul=mul*tmp;}len=200;while(ans.x[len]==0&&len>=1)len--;for(;len>=0;len--)putchar(ans.x[len]+'0');
}相关文章:

P1050 [NOIP2005 普及组] 循环
题目描述 乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天,他突然对数的正整数次幂产生了兴趣。 众所周知,22 的正整数次幂最后一位数总是不断的在重复 2,4,8,6,2,4,8,6…2,4,8,6,2,4,8,6… 我们说 22 的正整数次幂最后一位的循环长度…...
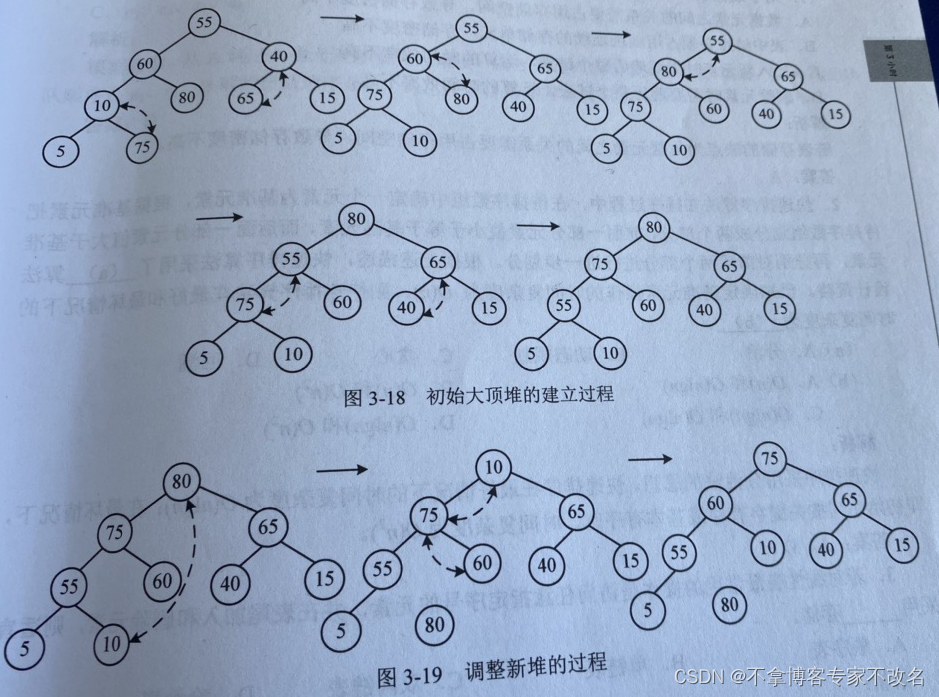
软考算法-排序篇-上
数据排序 一:故事背景二:直接插入排序2.1 概念2.2 画图表示2.3 代码实现2.4 总结提升 三:希尔排序3.1 概念3.2 画图表示3.3 代码实现3.4 总结提升 四:直接选择排序4.1 概念4.2 画图表示4.3 代码实现4.4 总结提升 五:堆…...

总结836
学习目标: 4月(复习完高数18讲内容,背诵21篇短文,熟词僻义300词基础词) 学习内容: 暴力英语:背诵《keep your direction》,默写,英语语法 高等数学:刷题&a…...

ginbuilder 工具快速创建
ginbuilder github 地址 快速创建一个ginweb项目: 目前apps下只有http服务,如果后续有需要的话,会添加上rpc服务,websocket服务后边如果有需要会添加上swagger 创建完成的目录结构 ├── apps │ ├── apis // 所有的apis…...

【Java基础面试宝典】堆、栈、方法区分别都存储了那些内容?wait 和 sleep 方法的区别?
目录 堆、栈、方法区分别都存储了那些内容? 堆(heap) 栈(stack) 方法区(method) 在 java 中 wait 和 sleep 方法的区别? 堆、栈、方法区分别都存储了那些内容? 堆&a…...

古剑飞仙手游Linux系统服务器架设教程
安装宝塔直接运行命令即可。 yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh 搭建环境: centos 7以上系统服务器 宝塔面板安装应用如下: Nginx1.14 mysql5.7 php5.6 1…...
(附python示例代码))
python实战应用讲解-【numpy数组篇】常用函数(十)(附python示例代码)
目录 Python Numpy MaskedArray.ravel()函数 Python Numpy MaskedArray.reshape()函数 Python Numpy MaskedArray.resize()函数 Python Numpy MaskedArray.std()函数 Python Numpy MaskedArray.sum()函数 Python Numpy MaskedArray.swapaxes()函数 Python Numpy MaskedA…...
练习题#2)
计算机组成原理(考研408)练习题#2
用于复习408或计算机组成原理期末考试。如有错误请在评论区指出。 So lets start studying with questions! それでは、問題の勉強を始めましょう! 11.某 cache 采用全相联映射,假设 cache 有 3 块,程序运行过程中需要访问的主存块号依 次为…...
Apache POI,springboot中导出excel报表
2. Apache POI 2.1 介绍 Apache POI 是一个处理Miscrosoft Office各种文件格式的开源项目。简单来说就是,我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作。 一般情况下,POI 都是用于操作 Excel 文件。 Apache POI 的应用场景…...
-- 三种样式表)
CSS(一)-- 三种样式表
目录 1. 行内样式表 2. 内部样式表 3. 外部样式表(即引入 .css文件)(重点掌握) 1. 行内样式表 行内样式表(内联样式表)是在元素标签内部的 style 属性中设定 CSS 样式。适合于修改简单样式。 <di…...

嵌入式之Samba服务器搭建
在嵌入式系统开发应用平台中,tftp、nfs和samba服务器是最常用的文件传输工具 tftp和nfs是在嵌入式Linux开发环境中经常使用的传输工具 samba则是Linux和Windows之间的文件传输工具。 下面演示在linux上搭建Samba服务器 sudo apt-get install samba chmod -R 77…...
vue3+go——看到了就去学习吧
vue3go——看到了就去学习吧 Vue3.2 Vite Element-Plus 实现最基础的 CRUD1.效果展示【02:36】2.创建项目【03:16】3.添加github管理【04:10】4.引入element-plus【04:21】5.内容布局【08:59】6.布局优化【05:31】7.添加弹窗【09:34】8.ref改$ref【02:47】9.新增数据【09:22】…...

Perf工具统计CPU性能
Perf 性能检测工具 Perf 是一个内置于Linux内核中的工具,用于性能分析和调优。它可以对系统的CPU使用情况、内存使用情况、磁盘I/O、网络I/O等进行监控和分析,并提供了丰富的分析和可视化工具,以帮助用户定位和解决性能问题。perf可以进行函…...
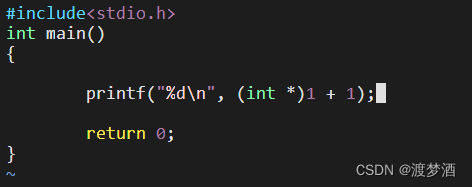
考验大家指针功底的时候到了:请问如何理解 (int*)1 + 1 ?
来,猜猜看,这里的执行结果是什么? 这是今天课上的一道理解题,给大家一点点思考时间。 (心里有答案了再往下滑哦) 5 4 3 2 1 . 答案是,报warning!因为%d不是用来输出指针的哈…...

英语基础-介词
介词 方位介词 in:在…里面 Its in the box. 在盒子里 in my backpack 在背包里 in the tree 长在树上on:在…上面(指与物体表面接触) Its on the box. 在盒子上(和盒子接触) on the floor.在地板上 on the tree.在树上under:在…下面 Its unde…...
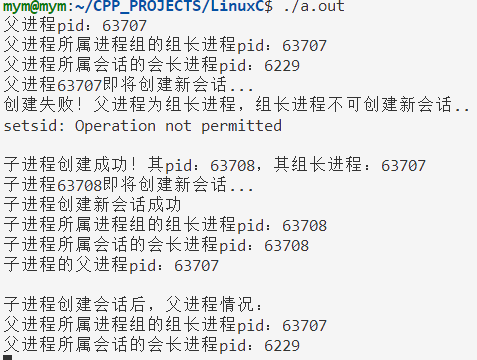
Linux进程通信:进程组 会话
1. 进程组 (1)概念:一个或多个进程的集合,也称为“作业”。 (2)父进程创建子进程时,默认属于同一个进程组。进程组ID为组长进程ID。 (3)进程组中只要有一个进程存在&a…...

【前端面经】JS-深浅拷贝
理解深浅拷贝 深浅拷贝问题的出现是由于JavaScript对不同类型的存储方式而引发的。 对于原始数据类型,它们的值是直接存储在栈内存中; 而复杂数据类型,则在栈内存中记录它的指针,而指针指向堆内存中真正的值。 所以对于原始数据类…...

【自然语言处理】实验2布置:Word2Vec TransE案例
NLP_class 学堂在线《自然语言处理》实验课代码报告,授课老师为刘知远老师。课程链接:https://www.xuetangx.com/training/NLP080910033761/1017121?channeli.area.manual_search。 持续更新中。 所有代码为作者所写,并非最后的“标准答案…...
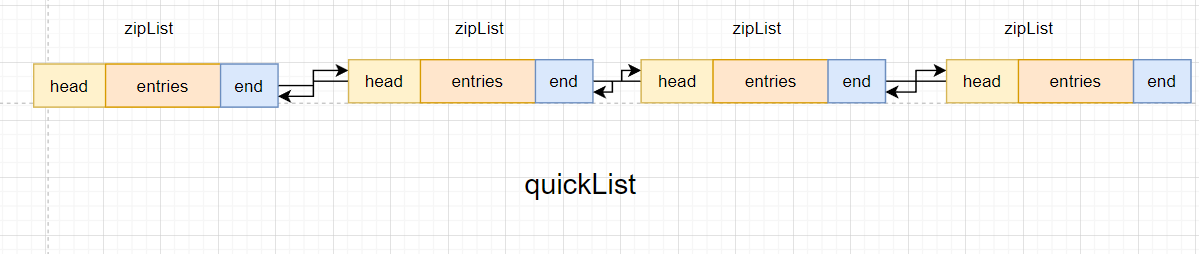
Redis集合底层实现原理
目录 本章重点简单动态字符串SDS集合底层实现原理zipListlistPackskipListquickListKey 与Value中元素的数量 本章重点 掌握Redis简单动态字符串了解Redis集合底层实现原理 简单动态字符串SDS SDS简介 我们Redis中无论是key还是value其数据类型都是字符串.我们Redis中的字符…...

OVS常用命令与使用总结
OVS常用命令与使用总结 说明 在平时使用ovs中,经常用到的ovs命令,参数,与举例总结,持续更新中… 进程启动 1.先准备ovs的工作目录,数据库存储路径等 mkdir -p /etc/openvswitch mkdir -p /var/run/openvswitch …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
