武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 + x 3 \int \frac{\rm dx}{1+x^3} ∫1+x3dx
解法一:
待定系数法:
∫ d x 1 + x 3 \int \frac{dx}{1+x^3} ∫1+x3dx
= ∫ d x ( 1 + x ) ( x 2 − x + 1 ) =\int \frac{dx}{(1+x)(x^2-x+1)} =∫(1+x)(x2−x+1)dx
= 1 3 ∫ ( 1 x + 1 + − x + 2 x 2 − x + 1 ) d x =\frac{1}{3} \int(\frac{1}{x+1} +\frac{-x+2}{x^2-x+1})\,{\rm d}x =31∫(x+11+x2−x+1−x+2)dx
= 1 3 [ ln ∣ x + 1 ∣ − 1 2 ∫ ( 2 x − 1 ) − 3 x 2 − x + 1 d x ] =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{2}\int\frac{(2x-1)-3}{x^2-x+1}\,{\rm d}x] =31[ln∣x+1∣−21∫x2−x+1(2x−1)−3dx]
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ∫ d ( x 2 − x + 1 ) x 2 − x + 1 + 1 2 ∫ 1 ( x − 1 2 ) 2 + 3 4 d x =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\int\frac{d(x^2-x+1)}{x^2-x+1}+\frac{1}{2}\int\frac{1}{(x-\frac{1}{2})^2+\frac{3}{4}}\,{\rm d}x =31[ln∣x+1∣−61∫x2−x+1d(x2−x+1)+21∫(x−21)2+431dx
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ln ∣ x 2 − x + 1 ∣ + 1 2 × 1 3 2 arctan x − 1 2 3 2 + C =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\ln\lvert x^2-x+1\rvert+\frac{1}{2}\times\frac{1}{\frac{\sqrt{3}}{2}}\arctan {\frac{x-\frac{1}{2}}{\frac{\sqrt{3}}{2}}}+C =31[ln∣x+1∣−61ln∣x2−x+1∣+21×231arctan23x−21+C
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ln ∣ x 2 − x + 1 ∣ + 1 3 arctan 2 x − 1 3 + C =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\ln\lvert x^2-x+1\rvert+\frac{1}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}+C =31[ln∣x+1∣−61ln∣x2−x+1∣+31arctan32x−1+C
草稿:
原式 = ∫ ( A x + 1 + B x + C x 2 − x + 1 ) d x 原式=\int( \frac{A}{x+1}+\frac{Bx+C}{x^2-x+1})\,{\rm d}x 原式=∫(x+1A+x2−x+1Bx+C)dx
则 A ( x 2 − x + 1 ) + ( B x + C ) ( x + 1 ) = 1 则A(x^2-x+1)+(Bx+C) (x+1)=1 则A(x2−x+1)+(Bx+C)(x+1)=1
即 A + B = 0 ; − A + B + C = 0 ; A + C = 1 即A+B=0;-A+B+C=0;A+C=1 即A+B=0;−A+B+C=0;A+C=1
解得 C = 2 3 , A = 1 3 , B = − 1 3 解得C=\frac{2}{3},A=\frac{1}{3},B= -\frac{1}{3} 解得C=32,A=31,B=−31
解法二:
灵活应用加项减项
可以看武忠祥老师每日一题||不定积分基础训练(三)
∫ 1 1 + x 3 d x \int \frac{1}{1+x^3}\,{\rm d}x ∫1+x31dx
= 1 2 ∫ ( 1 + x ) + ( 1 − x ) 1 + x 3 d x =\frac{1}{2}\int \frac{(1+x)+(1-x)}{1+x^3}\,{\rm d}x =21∫1+x3(1+x)+(1−x)dx
= 1 2 ∫ ( 1 + x ) + ( 1 − x ) ( 1 − x + x 2 ) ( 1 + x ) =\frac{1}{2}\int\frac{(1+x)+(1-x)}{(1-x+x^2)(1+x)} =21∫(1−x+x2)(1+x)(1+x)+(1−x)
= 1 2 [ 2 3 arctan 2 x − 1 3 + ln ∣ x + 1 ∣ − 1 3 ln ∣ x 3 + 1 ∣ ] + C =\frac{1}{2}[\frac{2}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}+\ln\lvert x+1\rvert-\frac{1}{3}\ln \lvert x^3+1 \rvert]+C =21[32arctan32x−1+ln∣x+1∣−31ln∣x3+1∣]+C
类题拓展:
∫ x 1 + x 3 d x \int \frac{x}{1+x^3}\,{\rm d}x ∫1+x3xdx
= 1 2 ∫ ( 1 + x ) − ( 1 − x ) 1 + x 3 d x =\frac{1}{2}\int \frac{(1+x)-(1-x)}{1+x^3}\,{\rm d}x =21∫1+x3(1+x)−(1−x)dx
= 1 2 [ 2 3 arctan 2 x − 1 3 − ( ln ∣ x + 1 ∣ − 1 3 ln ∣ x 3 + 1 ∣ ) ] + C =\frac{1}{2}[\frac{2}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}-(\ln\lvert x+1\rvert-\frac{1}{3}\ln \lvert x^3+1 \rvert)]+C =21[32arctan32x−1−(ln∣x+1∣−31ln∣x3+1∣)]+C
相关文章:
)
武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 x 3 \int \frac{\rm dx}{1x^3} ∫1x3dx 解法一: 待定系数法: ∫ d x 1 x 3 \int \frac{dx}{1x^3} ∫1x3dx ∫ d x ( 1 x ) ( x 2 − x 1 ) \int \frac{dx}{(1x)(x^2-x1)} ∫(1x)(x2−x1)dx 1 3 ∫ ( 1 x 1 − x 2 x 2 − x …...

记一次产线打印json导致的redis连接超时
服务在中午十一点上线后,服务每分钟发出三到四次redis连接超时告警。错误信息为: Dial err:dial tcp: lookup xxxxx: i/o timeout 排查过程 先是检查redis机器的情况,redis写入并发数较大,缓存中保留了一小时大概400w条数据。red…...

FPGA入门系列12--RAM的使用
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...

【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、为什么使用TypeScript?二、Vue 3和TypeScript…...

ffmpeg-mov-metadate不识别Bug修复
文章目录 BUG起因类似问题反馈问题解决具体步骤: 阅读过文章ffmpeg命令行解析调试流程记录movenc.c源码分析 BUG起因 在ffmpeg参数默认可识别的metadata参数如下: 具体可见libavformat/movenc.c->mov_write_udta_tag() mov_write_string_metadata(s,…...
(8.6) 引导程序更新)
(8)(8.6) 引导程序更新
文章目录 前言 1 我在哪里可以下载最新的引导程序? 2 使用任务规划器进行升级...
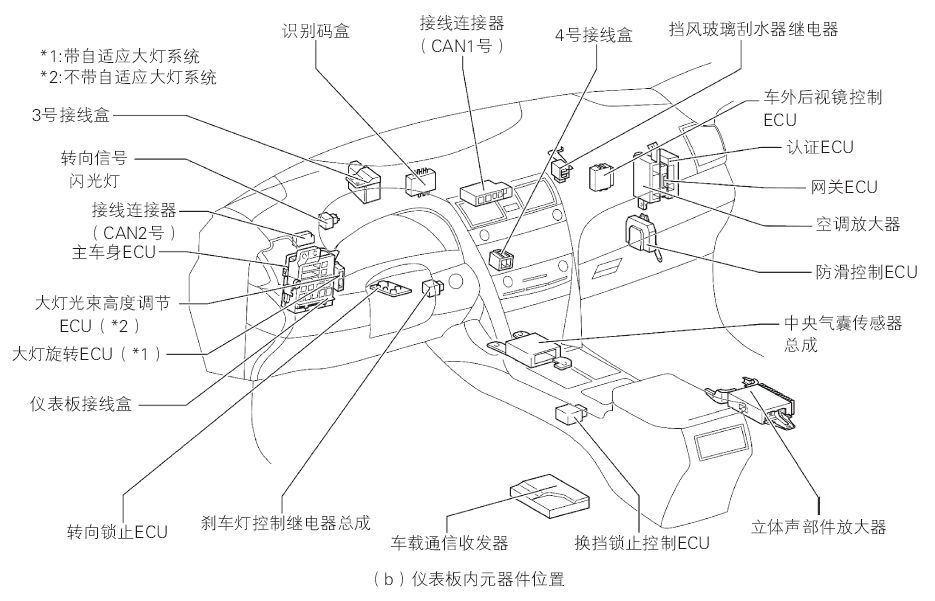
汽车电路图、原理框图、线束图、元器件布置图的识读技巧与要点
摘要: 想要读懂汽车电路图就必须把电的通路理清楚,即某条线是什么信号,该信号是输入信号、输出信号还是控制信号以及信号起什么作用,在什么条件下有信号,从哪里来,到哪里去。 一、汽车电路图的识读技巧 1.…...
( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II 难度:中等 给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件: 假设该列表是 answer [a1, a2, a3, ... , an] ࿰…...

【python基础语法七】python内置函数和内置模块
内置全局函数 abs 绝对值函数 print(abs(-1)) # 1 print(abs(100)) # 100round 四舍五入 """奇进偶不进(n.5的情况特定发生)""" res round(3.87) # 4 res round(4.51) # 5 # res round(2.5) # 2 # res round(3.5) # 4 res round(6.5) # …...

81. read readline readlines 读取文件的三种方法
81. read readline readlines 读取文件的三种方法 文章目录 81. read readline readlines 读取文件的三种方法1. 读取文件的三种方法2. read方法3. readline方法4. readlines方法5. 代码总结5.1 read方法读取全部内容5.2 readline方法读取一行,返回字符串5.3 readli…...

【社区图书馆】【图书活动第四期】
目录 一、前言 二、作者简介 三、《PyTorch高级机器学习实战》内容简介 四、书目录 一、前言 今天,偶尔逛到csdn社区图书馆,看到有活动 “【图书活动第四期】来一起写书评领实体奖牌红包电子勋章吧!”(活动到今天结束…...
)
webpack学习指南(上)
构建流程 Webpack 的构建流程可以分为以下几个步骤: 解析配置文件:Webpack 会读取项目中的 webpack.config.js 文件,并解析其中的配置项。 解析入口文件:Webpack 通过配置文件中设置的 entry 入口,递归地解析出所有依…...
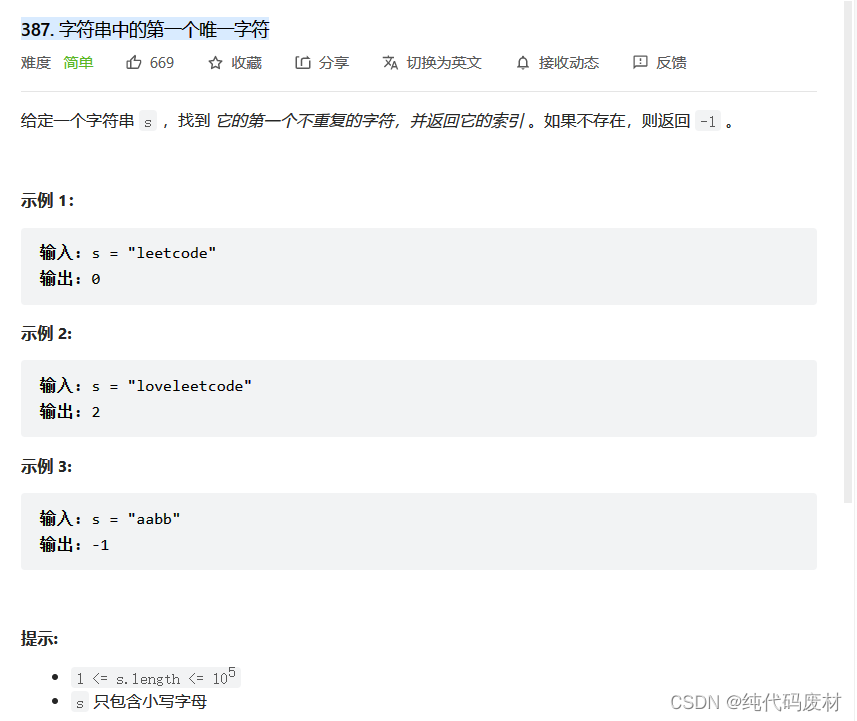
刷题记录˃ʍ˂
一、1033. 移动石子直到连续 思路 这道题是一道数学题,它一共分为三种可能 第一种可能为三个石子本来就是连续的时候 第二种可能为最少步数为1的时候,相邻石子不能大于一格 第三种可能为最少步数为2的时候,这时相邻石子大于一格 那么第二…...
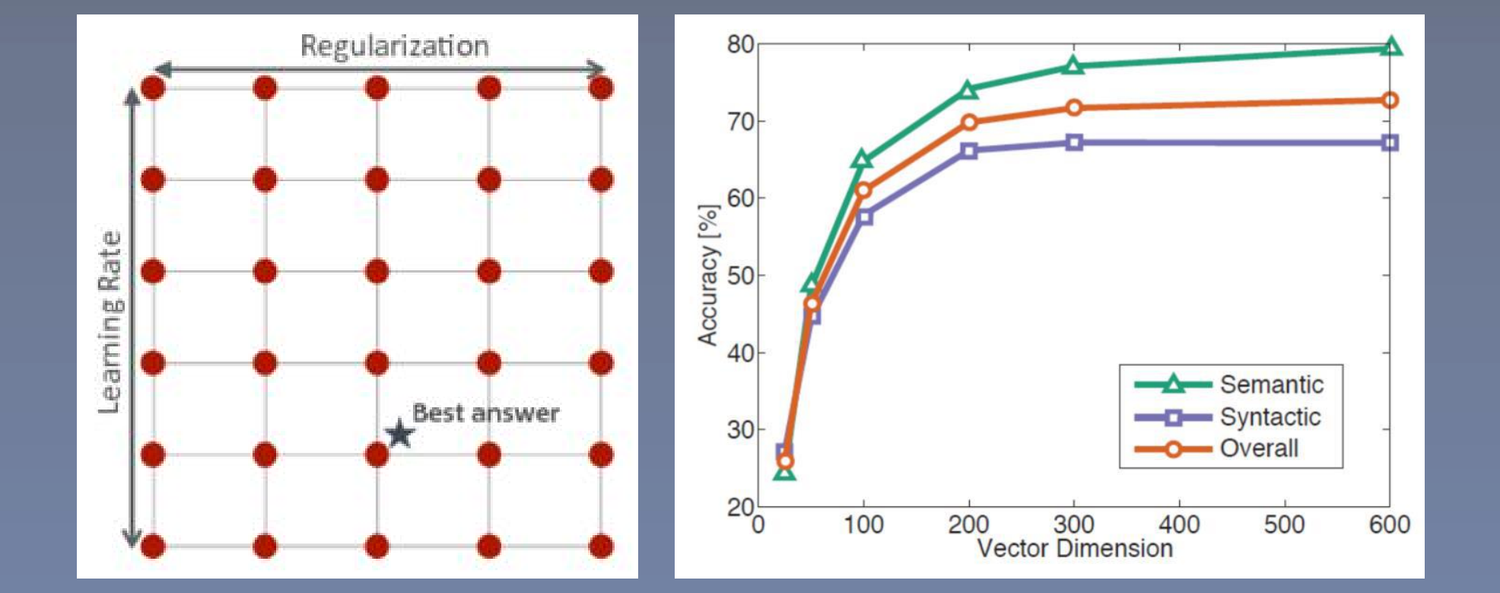
Word2vec原理+实战学习笔记(二)
来源:投稿 作者:阿克西 编辑:学姐 前篇:Word2vec原理实战学习笔记(一) 视频链接:https://ai.deepshare.net/detail/p_5ee62f90022ee_zFpnlHXA/6 5 对比模型(论文Model Architectur…...

什么是Java的多线程?
Java的多线程是指在同一时间内,一个程序中同时运行多个线程。每个线程都是一个独立的执行路径,可以独立地执行代码。Java中的多线程机制使得程序可以更高效地利用计算机的多核处理器和CPU时间,从而提高程序的性能和响应能力。 创建和使用Jav…...

“use strict“是什么? 使用它有什么优缺点?
严格模式 - JavaScript | MDN Javascript 严格模式详解 - 阮一峰的网络日志 1、"use strict" 是什么? "use strict" :指定代码在严格条件下执行; 2、 使用 "use strict" 有什么优缺点? ① 严格模式通过抛出错…...
【C++】C++11常用特性总结
哥们哥们,把书读烂,困在爱里是笨蛋! 文章目录 一、统一的列表初始化1.统一的{}初始化2.std::initializer_list类型的初始化 二、简化声明的关键字1.decltype2.auto && nullptr 三、STL中的一些变化1.新增容器:array &…...

泛型——List 优于数组
数组与泛型有很大的不同: 1. 数组是协变的(covariant) 意思是:如果Sub是Super的子类型,则数组类型Sub[] 是数组类型Super[] 的子类型。 2. 泛型是不变的(invariant) 对于任何两种不同的类型Ty…...

JavaScript中对象的定义、引用和复制
JavaScript是一种广泛使用的脚本语言,其设计理念是面向对象的范式。在JavaScript中,对象就是一系列属性的集合,每个属性包含一个名称和一个值。属性的值可以是基本数据类型、对象类型或函数类型,这些类型的值相互之间有着不同的特…...

JavaScript通过函数异常处理来输入圆的半径,输出圆的面积的代码
以下为实现通过函数异常处理来输入圆的半径,输出圆的面积的代码和运行截图 目录 前言 一、通过函数异常处理来输入圆的半径,输出圆的面积 1.1 运行流程及思想 1.2 代码段 1.3 JavaScript语句代码 1.4 运行截图 前言 1.若有选择,您可以…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
