【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。
区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。
border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] = s [ q , r ] s_{[l,p]}=s_{[q,r]} s[l,p]=s[q,r],显然直接跳 fail \text{fail} fail链即可。厉害的地方来了,对于两个相同的子串只用计算一次,而每跳一次至少会出现一对相同的子串,因此总转移数目只有 O ( n 2 ) O(n^2) O(n2)。
问题在于求出区间 [ l , r ] [l,r] [l,r]内最多能选多少个不重复的 s [ l , p ] s_{[l,p]} s[l,p]。更厉害的地方来了,这个东西可以倍增预处理,设 g l , r , k g_{l,r,k} gl,r,k表示和 s [ l , r ] s_{[l,r]} s[l,r]相同的不重叠的第 2 k 2^k 2k个串的左端点,然后就做完了。
复杂度是严格的 O ( n 2 log n ) O(n^2\log n) O(n2logn)。 当然减一减枝也能过。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n,nxt[2505][2505],to[2505][2505];
int trie[2505*2505][26],g[2505][2505][12],len[2505*2505],tot;
ll dp[2505][2505],A,B,C;
vector<int>pos[2505*2505];
string s;
void chmin(ll &x,ll y){x=min(x,y);}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>s;memset(dp,0x3f,sizeof dp);cin>>A>>B>>C;//fixedfor(int i=0;i<n;i++){nxt[i][i]=i-1;for(int j=i+1;j<n;j++){int k=nxt[i][j-1];while(k>=i&&s[k+1]!=s[j])k=nxt[i][k];if(s[k+1]==s[j])k++;nxt[i][j]=k;}}for(int i=0;i<n;i++){int it=0;for(int j=i;j<n;j++){if(!trie[it][s[j]-'a'])trie[it][s[j]-'a']=++tot,len[tot]=j-i+1;it=trie[it][s[j]-'a'];pos[it].pb(i);to[i][j]=it;}}for(int i=1;i<=tot;i++){sort(pos[i].begin(),pos[i].end());int k=0;for(int j=0;j<pos[i].size();j++){while(k<pos[i].size()&&pos[i][k]-pos[i][j]<len[i])k++;if(k!=pos[i].size()){g[pos[i][j]][len[i]][0]=pos[i][k];}}}for(int k=1;k<=11;k++){for(int i=0;i<n;i++){for(int j=1;j<=n-i;j++){if(g[i][j][k-1])g[i][j][k]=g[g[i][j][k-1]][j][k-1];}}}for(int i=0;i<n;i++)dp[i][i]=A;for(int len=2;len<=n;len++){for(int i=0;i<n-len+1;i++){int j=i+len-1;if(pos[to[i][j]][0]!=i){dp[i][j]=dp[pos[to[i][j]][0]][pos[to[i][j]][0]+len-1];continue;}chmin(dp[i][j],dp[i+1][j]+A);chmin(dp[i][j],dp[i][j-1]+A);//fixedfor(int k=nxt[i][j];k>=i;k=nxt[i][k]){int tot=1,nowl=i,len2=k-i+1;for(int l=11;l>=0;l--){if(g[nowl][len2][l]&&g[nowl][len2][l]<=j-len2+1){tot+=1<<l;nowl=g[nowl][len2][l];}}chmin(dp[i][j],dp[i][k]+B+tot*C+(len-tot*len2)*A);}}}cout<<dp[0][n-1];
}
相关文章:

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...
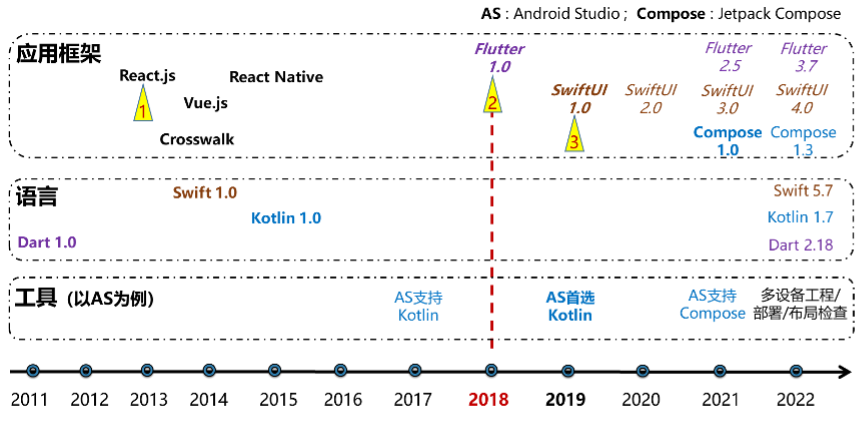
面向万物智联的应用框架的思考和探索(上)
原文:面向万物智联的应用框架的思考和探索(上),点击链接查看更多技术内容。 应用框架,是操作系统连接开发者生态,实现用户体验的关键基础设施。其中,开发效率和运行体验是永恒的诉求,…...

《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习,是一个交叉学科,是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期,使用专家设计的规则体系来设计。 缺点&…...

ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析,可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是: 内存池:Cl…...

docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现,基于 Linux 内核的 cgroup,namespace,以及 OverlayFS 类的 Union FS 等技术,对进程进行封装隔离,属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
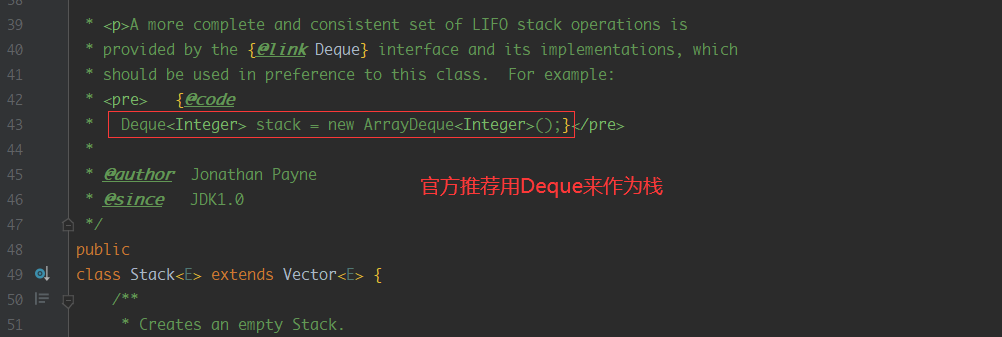
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则(最少知道原则)7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变,这个字,可能是需求变更、可能是场景变更&a…...
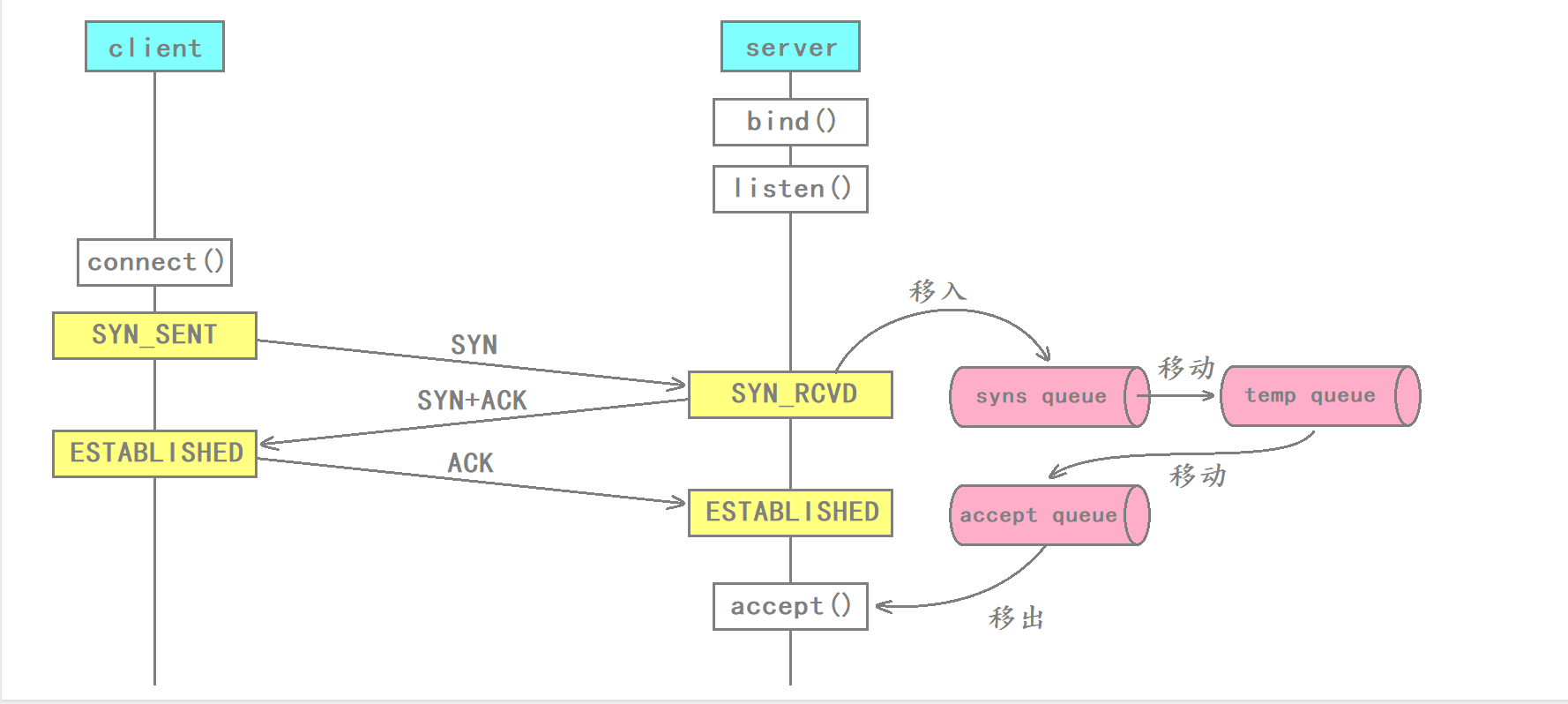
【Hello Network】TCP协议相关理解
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...

实施CRM目标有哪几步?如何制定CRM目标?
在当今竞争激烈的商业环境中,与客户建立持久的关系是企业重要的工作。CRM客户管理系统能有效帮助企业管理优化流程、管理客户,提高销售成功率,推动收入增长。那么您了解如何实施CRM吗?下面说说实施CRM目标是什么,如何设…...
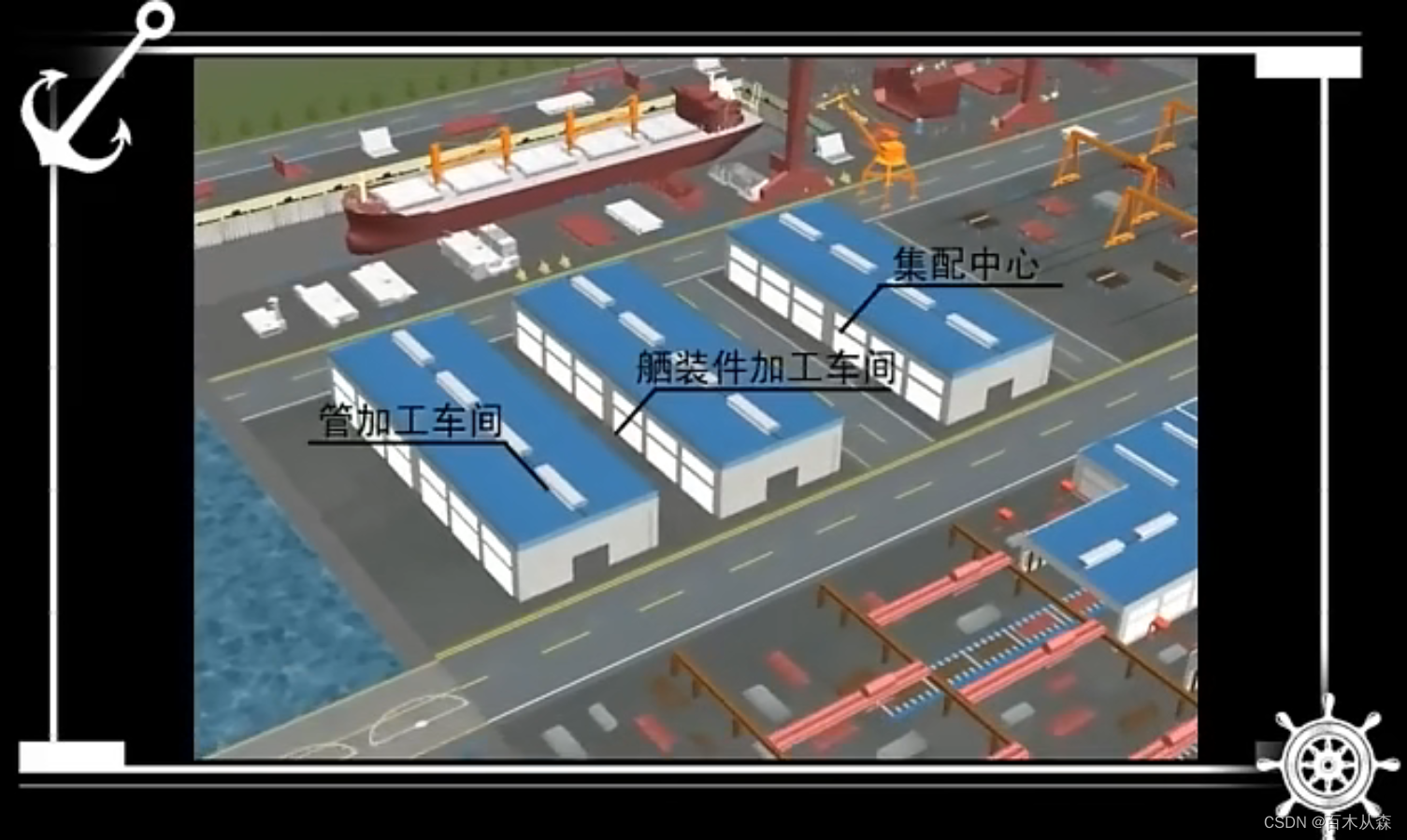
船舶建造概论(船舶建造工艺任务与现代造船模式)
船舶建造概论 1 船舶建造概论1.1 船舶建造工艺主要任务1.2 船舶建造流程(1)钢材料预处理(2) 钢材料加工(3)分段制作(4)总段制作(5)船台合拢(6&…...

项目内训(2023.5.6)
目录 Nacos是什么? 领域模型是什么? domain模块一般是干什么的? 在小乌龟中合并其他分支的作用是什么? nacos的配置文件 服务集群、服务提供、服务更加灵活庞大、消费服务、访问比较麻烦,A和B服务一起访问 系统结…...

【操作系统OS】学习笔记第二章 进程与线程(下)【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux命令集(Linux文件管理命令--rmdir指令篇)
Linux命令集(Linux文件管理命令--rmdir指令篇) Linux文件管理命令集(rmdir指令篇)5. rmdir(remove directory)1. 删除空的目录 folder12. 强制删除目录 folder1(包括非空目录)3. 递归删除目录及其目录下所有…...

在技术圈超卷的当下,学历到底是敲门砖还是枷锁?
前言 最近,突然之间被“孔乙己文学”刷屏了,短时间内“孔乙己文学”迅速走红,孔乙己是中国文学中的一位经典人物,他的长衫被认为是他的象征之一,孔乙己的长衫折射出很多现象,既有社会的,也有教育…...

Linux cgroup
前言 Cgroup和namespace类似,也是将进程进程分组,但是目的与namespace不一样,namespace是为了隔离进程组之前的资源,而Cgroup是为了对一组进程进行统一的资源监控和限制。 Cgroup的组成 subsystem 一个subsystem就是一个内核模…...
PID整定二:基于Ziegler-Nichols的频域响应
PID整定二:基于Ziegler-Nichols的频域响应 1参考2连续Ziegler-Nichols方法的PID整定2.1整定方法2.2仿真示例 1参考 1.1根轨迹图的绘制及分析 1.2计算机控制技术01-3.4离散系统的根轨迹分析法 1.3PID控制算法学习笔记 2连续Ziegler-Nichols方法的PID整定 2.1整定…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
