( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数
难度:中等
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O ( 1 ) O(1) O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
提示:
- 1 < = n < = 1 0 5 1 <= n <= 10^5 1<=n<=105
- nums.length == n + 1
- 1 <= nums[i] <= n
- nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
- 如何证明
nums中至少存在一个重复的数字? - 你可以设计一个线性级时间复杂度 O ( n ) O(n) O(n) 的解决方案吗?
💡思路:
法一:二分查找
由于数组中存储的数的范围是[1,n]且是连续的,所以我们可以进行二分查找,遍历数组统计小于等于数组中整数范围的中点mid的个数cnt:
- 如果
cnt > mid则重复的数一定在mid左边; - 否则一定在
mid的右边。 - 然后区间对半缩小,直到
l > h时,l即为重复的数。
法二:快慢指针
- 类似于有环链表中找出环的入口:
我们对 nums 数组建图,每个位置 i 连一条 i → nums[i]的边。由于存在的重复的数字 target,因此 target这个位置一定有起码两条指向它的边,因此整张图一定存在环,且我们要找到的 target 就是这个环的入口
对示例1进行建图,如下:
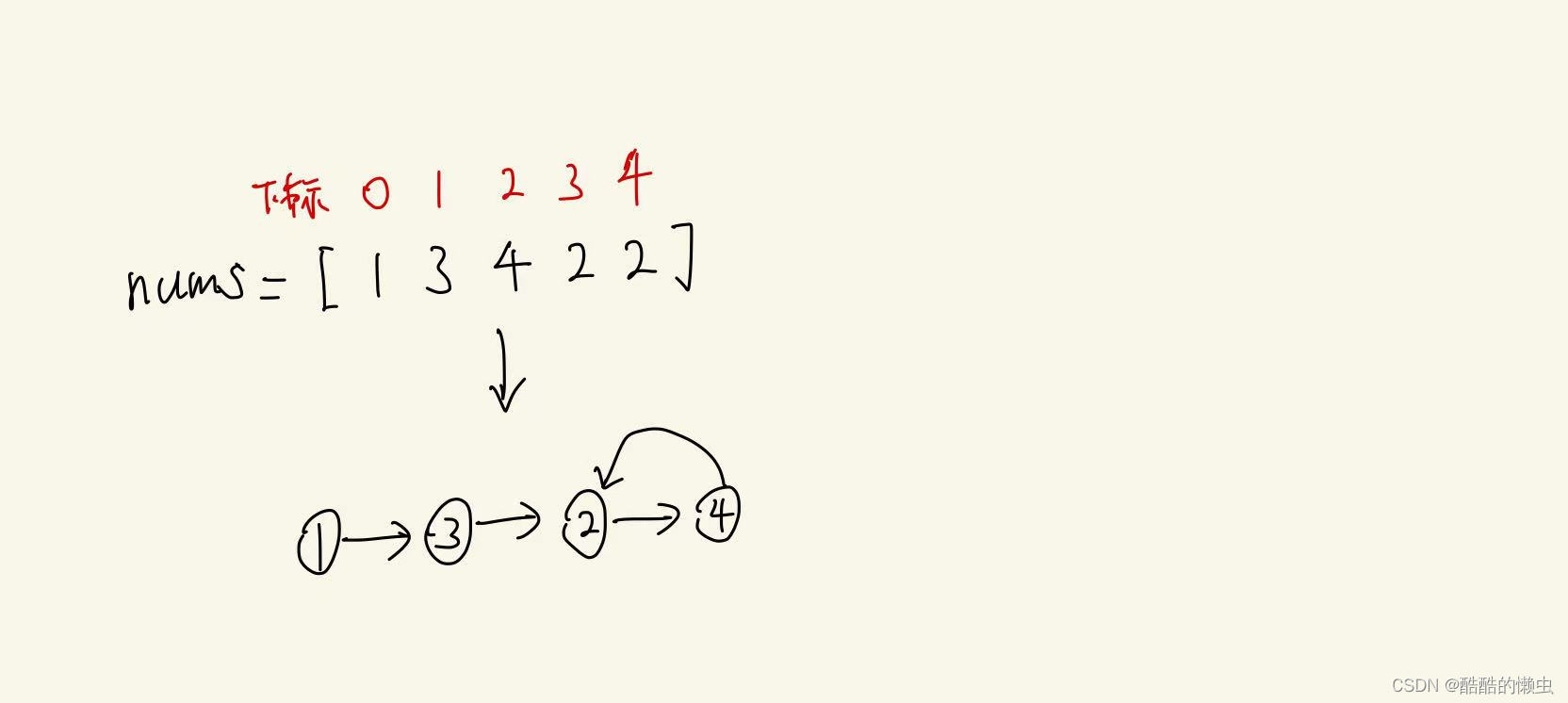
有两条边指向2,2即是环的入口,也是我们要找的target:
- 我们先设置慢指针
slow和快指针fast,慢指针每次走一步,快指针每次走两步,根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇; - 此时我们再将
slow放置起点0,两个指针每次同时移动一步,相遇的点就是答案。
这里简单证明为什么后面将
slow放置起点后移动相遇的点就一定是答案了。
假设环长为L,从起点到环的入口的步数是a,从环的入口继续走b步到达相遇位置,从相遇位置继续走c步回到环的入口,则有b+c= L,其中L、a、b、c都是正整数。
根据上述定义,慢指针走了
a+b步,快指针走了2(a+b)步。从另一个角度考虑,在相遇位置,快指针比慢指针多走了若干圈,因此快指针走的步数还可以表示成a+b+kL,其中k表示快指针在环上走的圈数。联立等式,可以得到:
2 ( a + b ) = a + b + k L 2(a+b)=a+b+kL 2(a+b)=a+b+kL
解得a = kL − b,整理可得:
a = ( k − 1 ) L + ( L − b ) = ( k − 1 ) L + c a=(k−1)L+(L−b)=(k−1)L+c a=(k−1)L+(L−b)=(k−1)L+c
从上述等式可知,如果慢指针从起点出发,快指针从相遇位置出发,每次两个指针都移动一步,则慢指针走了a步之后到达环的入口,快指针在环里走了k−1圈之后又走了c步,由于从相遇位置继续走c步即可回到环的入口,因此快指针也到达环的入口。两个指针在环的入口相遇,相遇点就是答案。
🍁代码:(Java、C++)
法一:二分查找
Java
class Solution {public int findDuplicate(int[] nums) {int l = 1, h = nums.length - 1;while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int num : nums){if(num <= mid){cnt++;}}if(cnt > mid) h = mid - 1;else l = mid + 1;}return l;}
}
C++
class Solution {
public:int findDuplicate(vector<int>& nums) {int l = 1, h = nums.size() - 1;while(l <= h){int mid = l + (h - l) / 2;int cnt = 0;for(int num : nums){if(num <= mid){cnt++;}}if(cnt > mid) h = mid - 1;else l = mid + 1;}return l;}
};
法二:快慢指针
Java
class Solution {public int findDuplicate(int[] nums) {int slow = nums[0], fast = nums[nums[0]];while(slow != fast){slow = nums[slow];fast = nums[nums[fast]];}slow = 0;while(slow != fast){slow = nums[slow];fast = nums[fast];}return slow;}
}
C++
class Solution {
public:int findDuplicate(vector<int>& nums) {int slow = nums[0], fast = nums[nums[0]];while(slow != fast){slow = nums[slow];fast = nums[nums[fast]];}slow = 0;while(slow != fast){slow = nums[slow];fast = nums[fast];}return slow;}
};
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中
n为 n u m s nums nums 数组的长度,「Floyd 判圈算法」时间复杂度为线性的时间复杂度;二分查找时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn), 二分查找最多需要二分 O ( l o g n ) O(logn) O(logn)。 - 空间复杂度: O ( 1 ) O(1) O(1),我们只需要常数空间存放若干变量。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度:中等 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。 你…...

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...
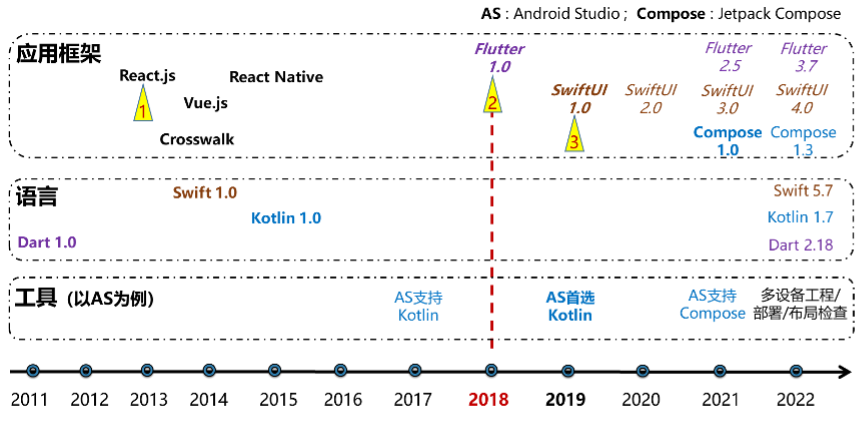
面向万物智联的应用框架的思考和探索(上)
原文:面向万物智联的应用框架的思考和探索(上),点击链接查看更多技术内容。 应用框架,是操作系统连接开发者生态,实现用户体验的关键基础设施。其中,开发效率和运行体验是永恒的诉求,…...

《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习,是一个交叉学科,是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期,使用专家设计的规则体系来设计。 缺点&…...

ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析,可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是: 内存池:Cl…...

docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现,基于 Linux 内核的 cgroup,namespace,以及 OverlayFS 类的 Union FS 等技术,对进程进行封装隔离,属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则(最少知道原则)7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变,这个字,可能是需求变更、可能是场景变更&a…...
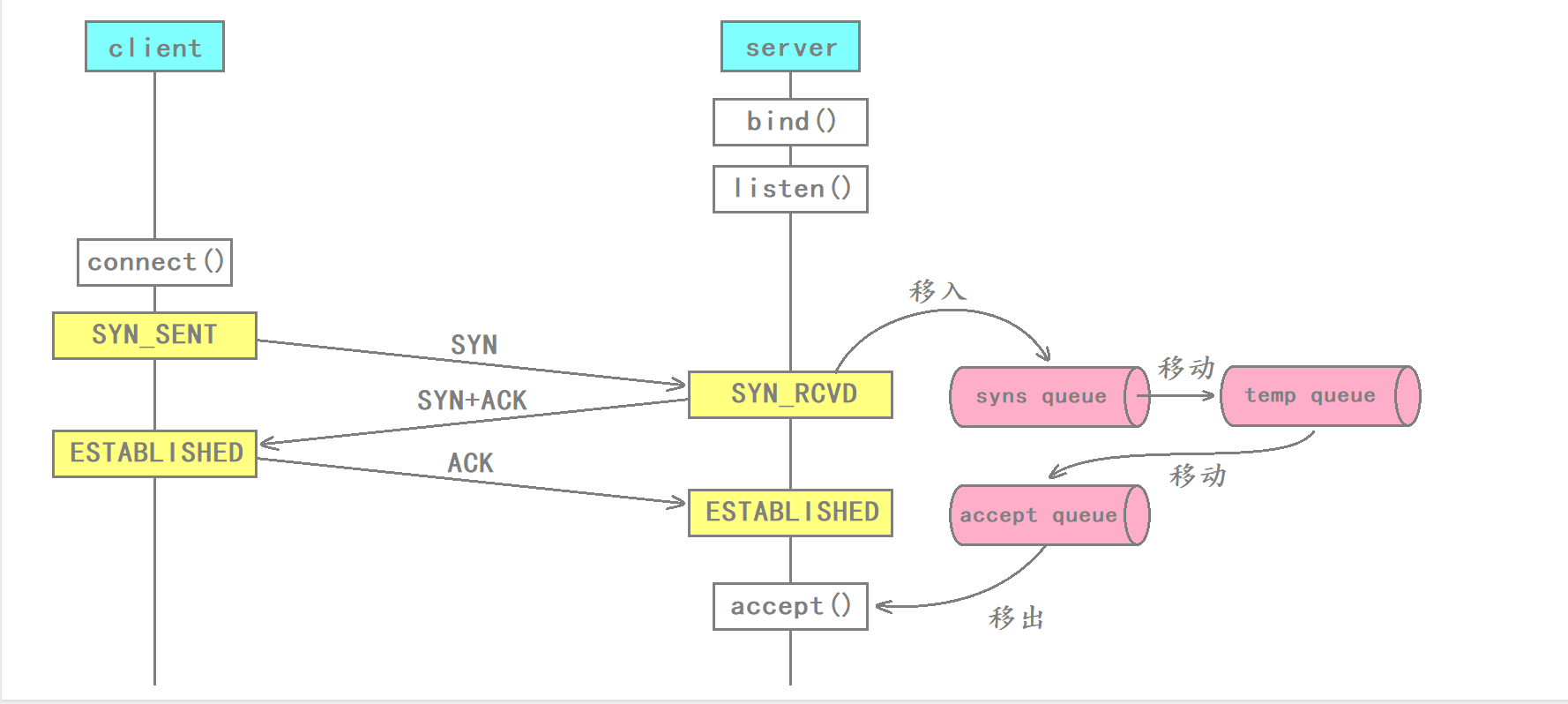
【Hello Network】TCP协议相关理解
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...

实施CRM目标有哪几步?如何制定CRM目标?
在当今竞争激烈的商业环境中,与客户建立持久的关系是企业重要的工作。CRM客户管理系统能有效帮助企业管理优化流程、管理客户,提高销售成功率,推动收入增长。那么您了解如何实施CRM吗?下面说说实施CRM目标是什么,如何设…...
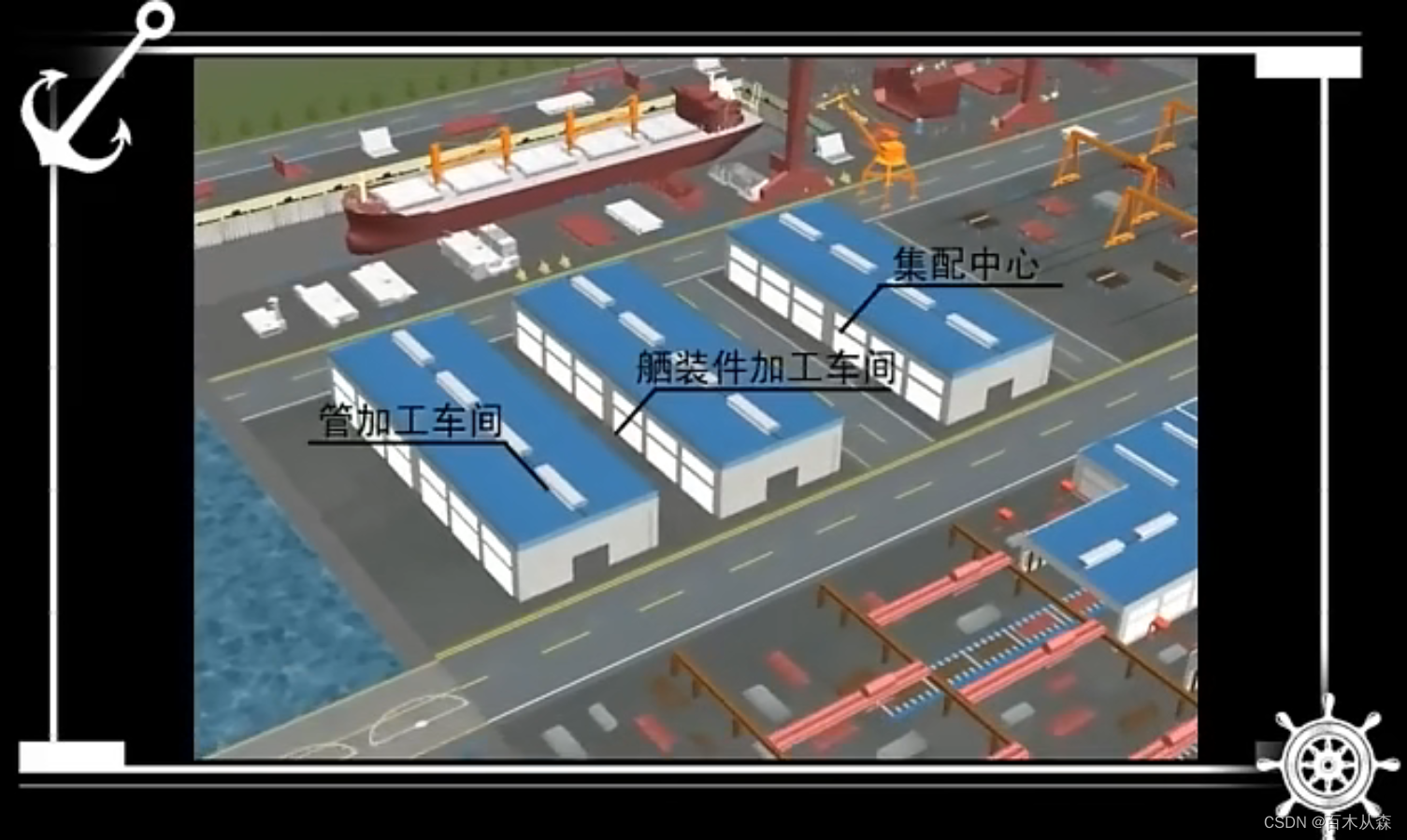
船舶建造概论(船舶建造工艺任务与现代造船模式)
船舶建造概论 1 船舶建造概论1.1 船舶建造工艺主要任务1.2 船舶建造流程(1)钢材料预处理(2) 钢材料加工(3)分段制作(4)总段制作(5)船台合拢(6&…...

项目内训(2023.5.6)
目录 Nacos是什么? 领域模型是什么? domain模块一般是干什么的? 在小乌龟中合并其他分支的作用是什么? nacos的配置文件 服务集群、服务提供、服务更加灵活庞大、消费服务、访问比较麻烦,A和B服务一起访问 系统结…...

【操作系统OS】学习笔记第二章 进程与线程(下)【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux命令集(Linux文件管理命令--rmdir指令篇)
Linux命令集(Linux文件管理命令--rmdir指令篇) Linux文件管理命令集(rmdir指令篇)5. rmdir(remove directory)1. 删除空的目录 folder12. 强制删除目录 folder1(包括非空目录)3. 递归删除目录及其目录下所有…...

在技术圈超卷的当下,学历到底是敲门砖还是枷锁?
前言 最近,突然之间被“孔乙己文学”刷屏了,短时间内“孔乙己文学”迅速走红,孔乙己是中国文学中的一位经典人物,他的长衫被认为是他的象征之一,孔乙己的长衫折射出很多现象,既有社会的,也有教育…...

Linux cgroup
前言 Cgroup和namespace类似,也是将进程进程分组,但是目的与namespace不一样,namespace是为了隔离进程组之前的资源,而Cgroup是为了对一组进程进行统一的资源监控和限制。 Cgroup的组成 subsystem 一个subsystem就是一个内核模…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
