分片上传和断点续传的区别?实现思路是什么?
相同:
分片上传和断点续传都是网络传输中常用的重要技术
不同:
-
分片上传:将一个大文件切分为多个小文件进行上传。这种方式能够加快上传速度,降低服务器压力,特别适用于大型文件的上传。例如,在云存储系统中,用户可以通过分片上传来上传大型视频、音频文件等。
-
断点续传:指在上传或下载过程中发生网络中断时,恢复传输时从上次中断的位置继续传输,而不必重新开始。这种方式可以节约时间和流量,提高网络的可靠性。例如,在网盘系统中,用户可以通过断点续传功能,避免文件上传或下载出现错误后需要重新从头开始的情况。
实现思路分别是什么?
断点续传的实现思路:
在文件上传之前,记录下已经上传的文件大小。
当文件上传过程中出现中断,保存当前已经上传的文件大小。
在再次上传文件时,使用 HTTP 协议中的 “Range” 头信息指定从上次中断的地方开始上传。
服务器端收到请求后,解析 “Range” 头信息,从指定的位置开始写入文件。
分片上传的实现思路:
将文件分成若干个小块。
对于每一块,单独上传。
服务器端收到请求后,将分片写入文件。
当所有分片都上传完成后,服务器端拼接所有分片,生成完整的文件。
注意,分片上传通常需要在服务器端配合使用,即服务器端需要支持将分片写入文件和拼接分片的功能。
总结
虽然分片上传和断点续传都基于把数据切分成小块,并结合特殊技术来处理,但是它们的应用场景略有不同。分片上传针对的是单个大文件的上传,而断点续传主要用于文件传输中的断点续传,满足用户在大文件上传/下载的过程中,网络出现异常时能够恢复上传或下载任务,节约时间和流量。
相关文章:

分片上传和断点续传的区别?实现思路是什么?
相同: 分片上传和断点续传都是网络传输中常用的重要技术 不同: 分片上传:将一个大文件切分为多个小文件进行上传。这种方式能够加快上传速度,降低服务器压力,特别适用于大型文件的上传。例如,在云存储系统…...
微前端 qiankun@2.10.5 源码分析(二)
微前端 qiankun2.10.5 源码分析(二) 我们继续上一节的内容。 loadApp 方法 找到 src/loader.ts 文件的第 244 行: export async function loadApp<T extends ObjectType>(app: LoadableApp<T>,configuration: FrameworkConfi…...

08异步请求:何种场景下应该使用异步请求?
异步在计算机科学中早就是一个比较常用的词汇,从操作系统的特性( 并发、共享、虚拟、异步)开始,异步就在处理并发操作中起到很大的作用,不仅如此,在软件层面,异步同样也是解决并发请求的一个关键过程,它可以将瞬时激增的请求进行更加灵活的处理,通过异步请求,客户端可…...

【深度学习 | Transformer】Transformers 教程:pipeline一键预测
文章目录 一、前言二、Computer vision2.1 Image classification2.2 Object detection2.3 Image segmentation2.4 Depth estimation 三、NLP3.1 Text classification3.2 Token classification3.3 Question answering3.4 Summarization3.5 Translation3.6 Language modeling3.6.…...
HTMLCSS
1、HTML 1.1 介绍 HTML 是一门语言,所有的网页都是用HTML 这门语言编写出来的,也就是HTML是用来写网页的,像京东,12306等网站有很多网页。 这些都是网页展示出来的效果。而HTML也有专业的解释 HTML(HyperText Markup Language)…...

【安装Nginx】
Linux上安装Nginx 文章目录 Linux上安装NginxUbuntuCentOS查看已安装的软件 Ubuntu 在 Ubuntu 上安装 Nginx 非常简单。只需按照以下步骤操作: 打开终端,更新软件包索引: sudo apt update安装 Nginx: sudo apt install nginx安…...

VSCode作业1:猜数字游戏和简单计数器(包含完整代码)
目录 猜数字游戏 一、使用‘random’函数获取随机数 二、 分情况讨论输入值大小情况 三、HTML代码 四、CSS样式及运行效果 简单计数器(计时器) 一、使用‘setInterval’函数实现计数效果 二、使用’clearInterval‘函数实现暂停计数和重新计数效果 …...

NANK OE骨传导开放式蓝牙耳机发布,极致体验拉满!
近日,中国专业音频品牌NANK南卡发布了全新一代——骨传导开放式蓝牙耳机NANK OE,耳机采用了传统真无线和骨传导的结合方式,带来更加舒适的佩戴体验和音质升级,同时还支持单双耳自由切换,全新的设计收获了市场的喜爱和认…...
看完这篇文章你就彻底懂啦{保姆级讲解}-----(I.MX6U驱动GPIO中断《包括时钟讲解》) 2023.5.9
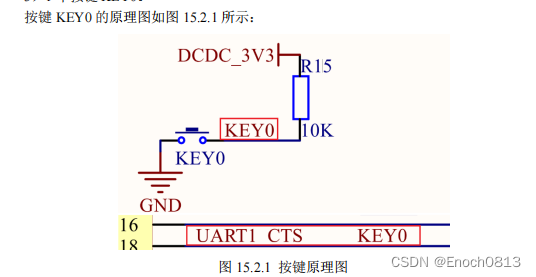
目录 前言整体文件结构源码分析(保姆级讲解)中断初始化部分初始化GIC控制器初始化中断向量表设置中断向量表偏移 系统时钟初始化部分使能所有的时钟部分led初始化部分beep初始化部分key初始化部分按键中断初始化部分按键中断服务函数部分 while循环部分 …...
MySql -- 事务
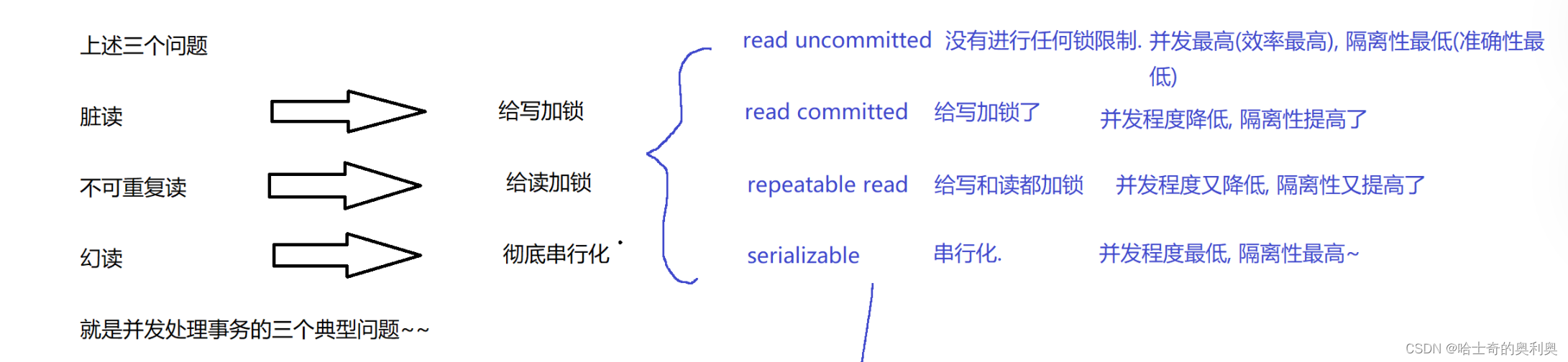
目录 1.概念 2.事务的运用场景 3.事务的四大特点 4.执行事务带来的问题 4.1 脏读 4.2 不可重复度 4.3 幻读 5. MySQL中事务的隔离级别 1.概念 事务就是把若干个独立操作打包成一个整体而诞生的一种功能. 2.事务的运用场景 比如:A——>B 转账500 A的余额-500…...

关于大模型对未来影响的一点看法
人们总是高估了未来一到两年的变化,低估了未来十年的变革。 ---比尔盖茨 近来OpenAI的GPT技术可以说在全球都带来了巨大的影响,也让大家看到了什么叫大力出奇迹。chatGPT和GPT4的能力给了大家很大的震撼,其流畅自如、逻辑清晰、出众的能力&am…...

Android - 约束布局 ConstraintLayout
一、概念 解决布局嵌套过多的问题,采用方向约束的方式对控件进行定位。 二、位置约束 2.1 位置 至少要保证水平和垂直方向都至少有一个约束才能确定控件的位置。 layout_constraintLeft_toLeftOf我的左边,与XXX左边对齐。layout_constraintLeft_toRight…...

Addictive Multiplicative in NN
特征交叉是特征工程中的重要环节,在以表格型(或结构化)数据为输入的建模中起到了很关键的作用。 特征交互的作用,一是尽可能挖掘对目标有效的模式、特征,二是具有较好的可解释性,三是能够将对数据的洞见引…...
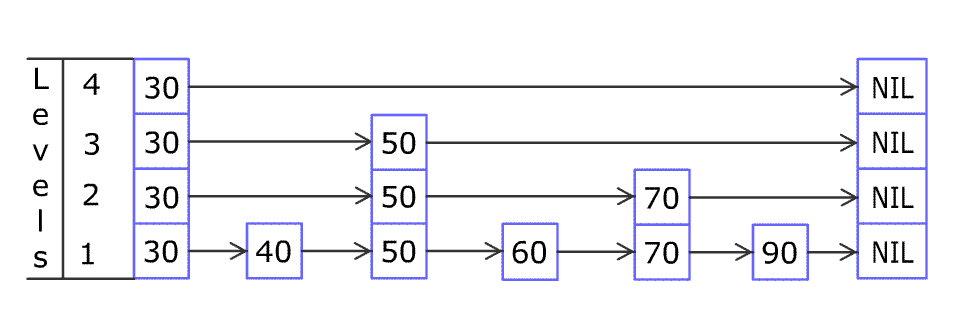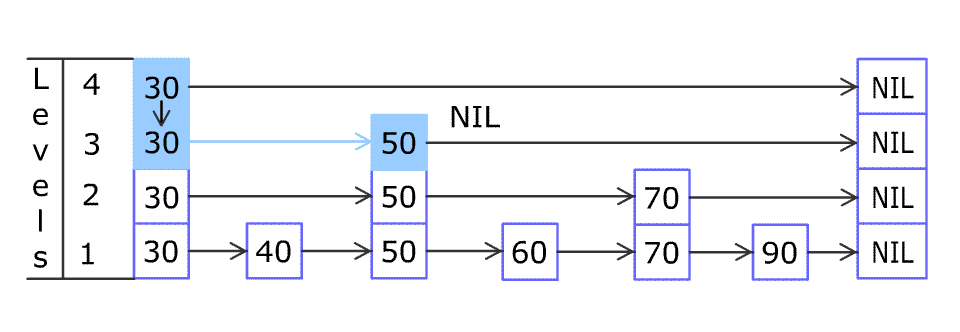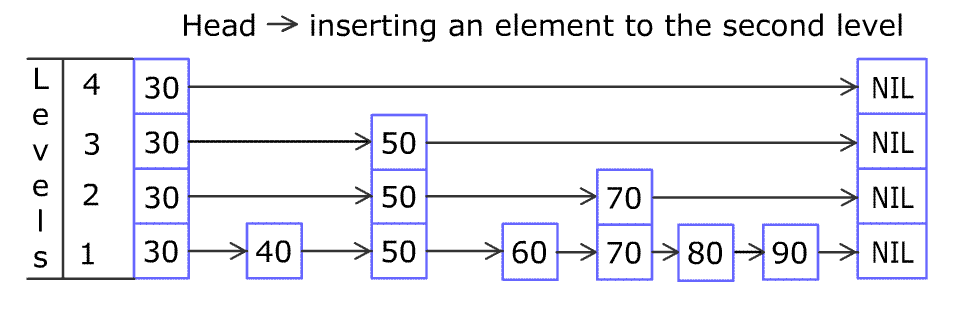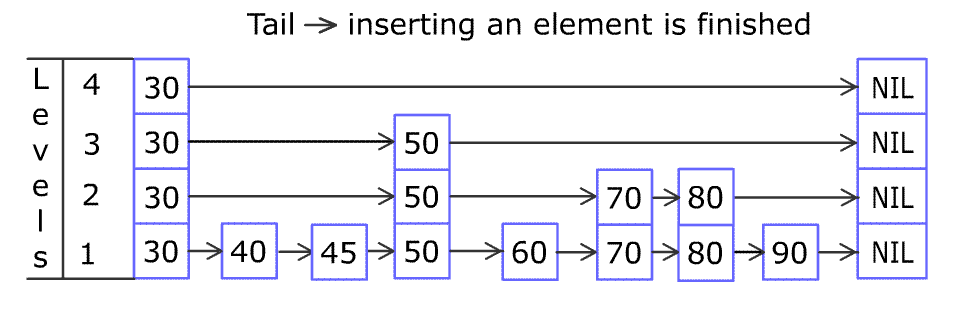
LeetCode 1206. 实现跳表
不使用任何库函数,设计一个跳表。 跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。 例如,一个跳表包…...
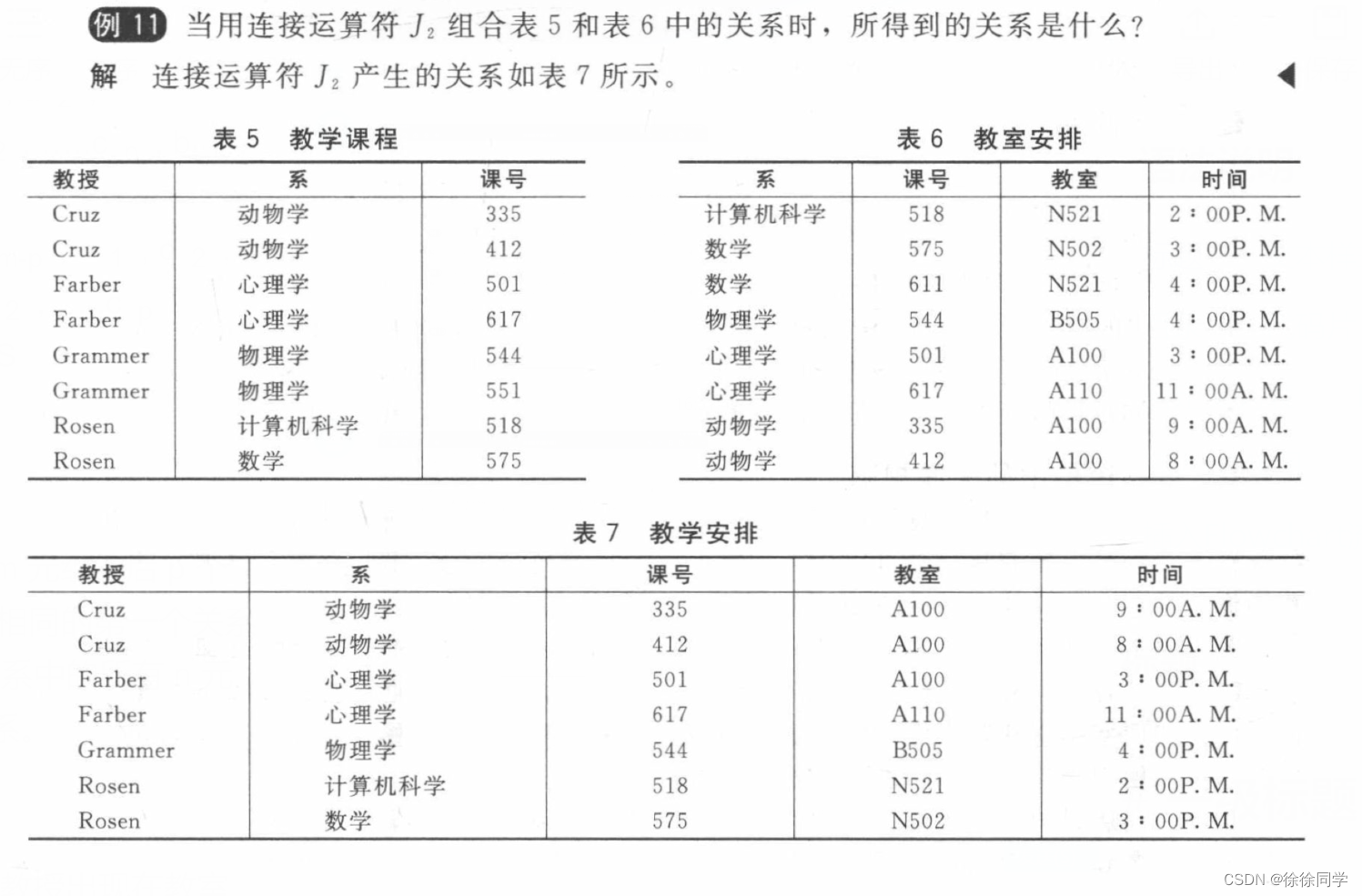
离散数学_九章:关系(2)
9.2 n元关系及其应用 1、n元关系,关系的域,关系的阶2、数据库和关系 1. 数据库 2. 主键 3. 复合主键 3、n元关系的运算 1. 选择运算 (Select) 2. 投影运算 (Project) 3. 连接运算 (Join) n元关系:两个以上集合的元素间的关系 1、n元关系…...

[ubuntu][原创]通过apt方式去安装libnccl库
ubuntu18.04版本安装流程: wget https://developer.download.nvidia.com/compute/cuda/repos/ubuntu1804/x86_64/cuda-ubuntu1804.pin sudo mv cuda-ubuntu1804.pin /etc/apt/preferences.d/cuda-repository-pin-600 sudo apt-key adv --fetch-keys https://develo…...

YonLinker连接集成平台构建新一代产业互联根基
近日,由用友公司主办的“2023用友BIP技术大会“在用友产业园(北京)盛大召开,用友介绍了更懂企业业务的用友BIP-iuap平台,并发布了全面数智化能力体系,助力企业升级数智化底座,加强加速数智化推进…...

泛型的详解
泛型的理解和好处 首先我们先来看看泛型的好处 1)编译时,检查添加元素的类型,提高了安全性 2)减少了类型转换的次数,提高效率[说明] 不使用泛型 Dog -> Object -> Dog//放入到ArrayList 会先转成Object,在取出时&#x…...

用科技创造未来!流辰信息技术助您实现高效办公
随着社会的迅猛发展,科技的力量无处不见。它正在悄悄地改变整个社会,让人类变得进步和文明,让生活变得便捷和高效。在办公自动化强劲发展的今天,流辰信息技术让通信业、电网、汽车、物流等领域的企业实现了高效办公,数…...

基于R语言APSIM模型
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。 APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
