RSA--维纳攻击--代码和题目分析
文章目录
- 维纳攻击原理:
- 维纳攻击脚本
- [羊城杯 2020]RRRRRRRSA 1
- 题目描述:
- 题目分析:
- 收获与体会:
维纳攻击原理:
两位大佬讲得非常清楚(搬运工就是我):https://zhuanlan.zhihu.com/p/400818185
https://www.cnblogs.com/wandervogel/p/16805992.html
看完详细原理后,我们来划重点


维纳攻击脚本
看得懂但写不出,只能搬运了
(注:看脚本前,必须对 ‘连分数’ 和 ‘渐近分数’ 的概念有清晰的认识:连分数 & 渐近分数)



所以说所求的d即为满足条件的渐近分数的分子(现在不理解是分子不要紧,自行推理完之后便可理解)
def transform(x, y): # 使用辗转相处将分数 x/y 转为连分数的形式res = []while y:res.append(x // y)x, y = y, x % yreturn resdef continued_fraction(sub_res):numerator, denominator = 1, 0for i in sub_res[::-1]: # 从sublist的后面往前循环denominator, numerator = numerator, i * numerator + denominatorreturn denominator, numerator # 得到渐进分数的分母和分子,并返回# 求解每个渐进分数
def sub_fraction(x, y):res = transform(x, y)res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res))))) # 将连分数的结果逐一截取以求渐进分数return resdef get_pq(a, b, c): # 由p+q和pq的值通过维达定理来求解p和qpar = gmpy2.isqrt(b * b - 4 * a * c) # 由上述可得,开根号一定是整数,因为有解x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)return x1, x2def wienerAttack(e, n):for (d, k) in sub_fraction(e, n): # 用一个for循环来注意试探e/n的连续函数的渐进分数,直到找到一个满足条件的渐进分数if k == 0: # 可能会出现连分数的第一个为0的情况,排除continueif (e * d - 1) % k != 0: # ed=1 (mod φ(n)) 因此如果找到了d的话,(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)continuephi = (e * d - 1) // k # 这个结果就是 φ(n)px, qy = get_pq(1, n - phi + 1, n)if px * qy == n:p, q = abs(int(px)), abs(int(qy)) # 可能会得到两个负数,负负得正未尝不会出现d = gmpy2.invert(e, (p - 1) * (q - 1)) # 求ed=1 (mod φ(n))的结果,也就是e关于 φ(n)的乘法逆元dreturn dprint("该方法不适用")c =
n =
e =
d = wienerAttack(e, n)
m=pow(c, d, n)
print(long_to_bytes(m))
-
此处再加一个欧拉函数的计算公式:

-
回到上面那个问题
不理解 d 为什么为分子的可以就用上述 89 / 26 这个例子用笔(即写纸上)进行代码推理,相信我,推理完后一定理解(我就是这样理解过来的)此串代码求解正常的RSA维纳攻击题型可解
但对于转了一点弯的题目便要稍作修改
而懂得修改的前提是你对以上的原理和代码完全理解
不理解就只能做简单的题型
举个栗子
[羊城杯 2020]RRRRRRRSA 1
题目描述:
import hashlib
import sympy
from Crypto.Util.number import *flag = 'GWHT{************}'flag1 = flag[:19].encode() #两截flag
flag2 = flag[19:].encode()
assert(len(flag) == 38)P1 = getPrime(1038)
P2 = sympy.nextprime(P1) #p2>p1
assert(P2 - P1 < 1000)Q1 = getPrime(512)
Q2 = sympy.nextprime(Q1) #q2>q1N1 = P1 * P1 * Q1
N2 = P2 * P2 * Q2E1 = getPrime(1024)
E2 = sympy.nextprime(E1)m1 = bytes_to_long(flag1)
m2 = bytes_to_long(flag2)c1 = pow(m1, E1, N1)
c2 = pow(m2, E2, N2)output = open('secret', 'w')
output.write('N1=' + str(N1) + '\n')
output.write('c1=' + str(c1) + '\n')
output.write('E1=' + str(E1) + '\n')
output.write('N2=' + str(N2) + '\n')
output.write('c2=' + str(c2) + '\n')
output.write('E2=' + str(E2) + '\n')
output.close()N1=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1=55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2=39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
题目分析:
- wiener attack 是依靠连分数进行的攻击方式,适用于非常接近某一值(比如1)时,求一个比例关系(通常是e / N = 1)
- 此题中e比较大,想到维纳攻击,但题中 e / N << 1, 不符合利用条件,但是N1和N2的关系却合适

- 注意:使用维纳攻击进行解题需满足一定的数值条件:
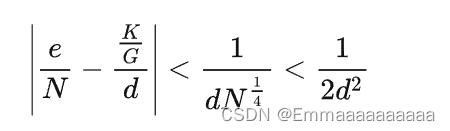
- 解题代码:
import gmpy2
from Crypto.Util.number import *
import sympy
def continuedFra(x, y):"""计算连分数:param x: 分子:param y: 分母:return: 连分数列表"""cf = []while y:cf.append(x // y)x, y = y, x % yreturn cf
def gradualFra(cf):"""计算传入列表最后的渐进分数:param cf: 连分数列表:return: 该列表最后的渐近分数"""numerator = 0 # 分子denominator = 1 # 分母for x in cf[::-1]:# 这里的渐进分数分子分母要分开numerator, denominator = denominator, x * denominator + numeratorreturn numerator, denominator
def solve_pq(a, b, c):"""使用韦达定理解出pq,x^2−(p+q)∗x+pq=0:param a:x^2的系数:param b:x的系数:param c:pq:return:p,q"""par = gmpy2.isqrt(b * b - 4 * a * c)return (-b + par) // (2 * a), (-b - par) // (2 * a)
def getGradualFra(cf):"""计算列表所有的渐近分数:param cf: 连分数列表:return: 该列表所有的渐近分数"""gf = []for i in range(1, len(cf) + 1):gf.append(gradualFra(cf[:i]))return gfdef wienerAttack(e, n):""":param e::param n::return: 私钥d"""cf = continuedFra(e, n)gf = getGradualFra(cf)for q2,q1 in gf: # 不得不说最后要倒一下呀!if q1 == 0: continueif N2 % q2 == 0 and q2 != 1:# 此处也可写成 N1 % q1 == 0 and q1 != 1(所以说要对原理清楚以及清楚求出的到底是哪个参数)return q2N1=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1=55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103
N2=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2=39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393
Q2=wienerAttack(N1,N2)
Q1 = sympy.prevprime(Q2)
P1 = gmpy2.iroot(N1 // Q1,2)[0]
P2 = sympy.nextprime(P1)
phi1 = P1 * (P1 - 1) * (Q1 - 1)
phi2 = P2 * (P2 - 1) * (Q2 - 1)
d1 = gmpy2.invert(E1,phi1)
d2 = gmpy2.invert(E2,phi2)
m1 = pow(c1,d1,N1)
m2 = pow(c2,d2,N2)
print(long_to_bytes(m1))
print(long_to_bytes(m2))# b'GWHT{3aadab41754799'
# b'f978669d53e64a3aca}'
收获与体会:

- e 很大时想到维纳攻击
- 任何比例非常接近另外一个已知比例情况下想到维纳攻击
这是第二次学习维纳攻击,第一次就看了个大概过程,但看完第二遍才发现第一次学习时貌似啥也没学到,仅仅只是草草了事,代码也是不求甚解,只求能解当时遇到的题就行。第二遍学习中,看得比较仔细,不懂的也会及时查找资料,比如渐近分数概念,比如不懂为什么d是分子便会借助稿纸推导。
所以说,欠下的债终究是要还的!
所以说,不能只为解题而解题,理解题目背后的原理并且举一反三才是我们的最终目标!
参考:[羊城杯 2020]RRRRRRRSA 题解(wiener attack运用)
相关文章:

RSA--维纳攻击--代码和题目分析
文章目录 维纳攻击原理:维纳攻击脚本[羊城杯 2020]RRRRRRRSA 1题目描述:题目分析: 收获与体会: 维纳攻击原理: 两位大佬讲得非常清楚(搬运工就是我):https://zhuanlan.zhihu.com/p/…...
飞腾ft2000-麒麟V10-SP1安装Docker、运行gitlab容器
目录 一、安装及配置docker 1、卸载docker相关包及删除相关配置文件 2、安装二进制docker 1.下载软件包 2.解压 3.修改镜像加速地址 4.修改profile文件 5.启动docker 6.docker常用命令 二、安装并启动gitlab镜像 1.安装gitlab镜像 1.查询满足使用需求的gitlab版本 2…...
C++ 的类型转换
目录 1. C语言中的类型转换 2. C强制类型转换 2.1static_cast 2.2 reinterpret_cast 2.3 const_cast 2.4 dynamic_cast 3. RTTI(了解) 1. C语言中的类型转换 在 C 语言中,如果 赋值运算符左右两侧类型不同,或者形参与实参类型不…...

【Windows】普通控制台EXE程序转为windows服务方式运行的详细步骤
背景 NSSM(Non-Sucking Service Manager)是一个免费的第三方Windows服务管理器,可以将任何可执行文件转换为Windows服务。官网下载地址为:https://nssm.cc/download 以下是NSSM配置Windows服务的详细步骤和注意事项: …...
NSSCTF [suctf 2019]hardcpp WP 控制流混淆
下载文件,64位主函数非常多循环 去控制流混淆,脚本下载deflat 用法 python 脚本名 文件名 起始地址例如主函数地址是0x4007E0 python deflat.py hardCpp 0x4007E0然后就生成了去混淆的文件 主函数非常大,开始分析逻辑 puts("func(?…...

计算机毕业论文内容参考|基于神经网络的网络安全态势感知技术研究
文章目录 导文文章重点摘要前言绪论课题背景国内外现状与趋势课题内容相关技术与方法介绍技术分析技术设计技术实现总结与展望导文 基于神经网络的网络安全态势感知技术研究 文章重点 摘要 随着互联网的快速发展,网络攻击的频率和复杂度也在逐年增加。为了更好地保护信息系统…...

Flask框架之Request、Response、Cookies、Session等对象的使用
Request、Response、Cookies、Session等对象的使用 Request对象基本使用参数的获取转换器内置转换器自定义转换器 Response对象基本使用返回模板重定向返回JSON Cookies对象设置cookie获取cookie删除cookie Session会话对象设置SECRET_KEY设置会话获取会话释放会话 Request对象…...
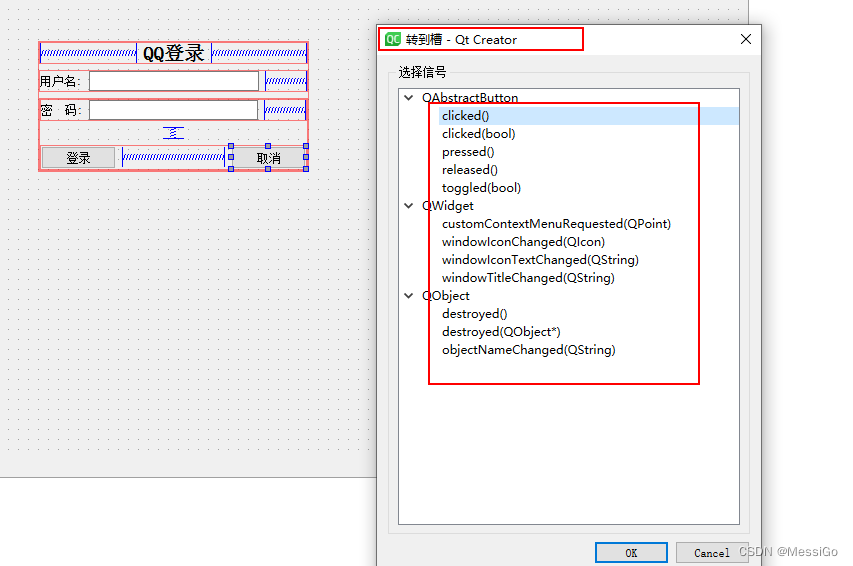
信号与槽机制一
一、信号与槽 1、什么是信号与槽? 信号和槽是用于对象之间的通信,它是Qt的核心机制,在Qt编程中有着广泛的应用。如果想学好Qt,一定要充分掌握信号的槽的概念与使用。 2、信号和槽的代码实例 在Qt中,发送对象、发送的信…...

nodejs 复制文件到指定目录
var fs require(fs), path require(path), exec require(child_process).exec, sourcePath, targetPath; //获取命令行中的路径 process.argv.forEach(function (val, index, array) { if (index 2) { sourcePath val; } if (index 3) { targetPath val; } }); // 定义…...
第八章 使用Apache服务部署静态网站
文章目录 第八章 使用Apache服务部署静态网站一、网站服务程序1、网站服务介绍2、Apache程序介绍 二、配置服务文件参数1、Linux系统中的配置文件2、配置httpd服务程序时最常用的参数以及用途描述 三、SELinux安全子系统1、SELinux介绍2、SELinux服务配置模式3、Semanage命令4、…...
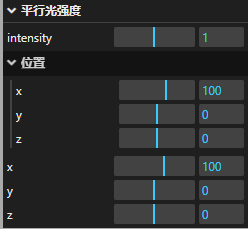
Three——四、几何体、高光网络材质、锯齿模糊以及GUI库的使用
文章: Three——一、初识Three以及基础的前端场景搭建(结尾含源码)Three——二、加强对三维空间的认识Three——三、动画执行、画布大小、渲染帧率和相机适配体验Three——四、几何体、高光网络材质、锯齿模糊以及GUI库的使用Three——五、点线模型对象、三角形概念…...
盲目自学网络安全只会成为脚本小子?
前言:我们来看看怎么学才不会成为脚本小子 目录: 一,怎么入门? 1、Web 安全相关概念(2 周)2、熟悉渗透相关工具(3 周)3、渗透实战操作(5 周)4、关注安全圈动…...

文从字顺|程序员须知,如何编写高质量代码
高质量代码是软件开发中至关重要的一部分。高质量的代码不仅可以提高软件的可维护性和可复用性,还可以增强软件的安全性和稳定性。同时,可以降低软件维护成本,提升开发效率,为用户提供更好的使用体验。 写出高质量代码是每个程序…...
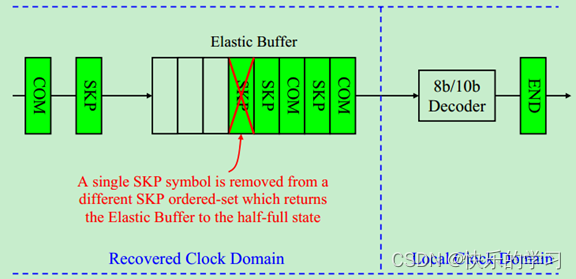
PCIe物理层弹性缓存机制(详细)解析-PCIe专题知识(四)
目录 前言一、简介二、详细解析2.1 实例解析2.2 具体实现过程 三、总结四、其他相关链接1、PCI总线及发展历程总结2、PCIe物理层总结-PCIE专题知识(一)3、PCIe数据链路层图文总结-PCIe专题知识(二)4、PCIe物理层链路训练和初始化总…...

分片上传和断点续传的区别?实现思路是什么?
相同: 分片上传和断点续传都是网络传输中常用的重要技术 不同: 分片上传:将一个大文件切分为多个小文件进行上传。这种方式能够加快上传速度,降低服务器压力,特别适用于大型文件的上传。例如,在云存储系统…...
微前端 qiankun@2.10.5 源码分析(二)
微前端 qiankun2.10.5 源码分析(二) 我们继续上一节的内容。 loadApp 方法 找到 src/loader.ts 文件的第 244 行: export async function loadApp<T extends ObjectType>(app: LoadableApp<T>,configuration: FrameworkConfi…...

08异步请求:何种场景下应该使用异步请求?
异步在计算机科学中早就是一个比较常用的词汇,从操作系统的特性( 并发、共享、虚拟、异步)开始,异步就在处理并发操作中起到很大的作用,不仅如此,在软件层面,异步同样也是解决并发请求的一个关键过程,它可以将瞬时激增的请求进行更加灵活的处理,通过异步请求,客户端可…...

【深度学习 | Transformer】Transformers 教程:pipeline一键预测
文章目录 一、前言二、Computer vision2.1 Image classification2.2 Object detection2.3 Image segmentation2.4 Depth estimation 三、NLP3.1 Text classification3.2 Token classification3.3 Question answering3.4 Summarization3.5 Translation3.6 Language modeling3.6.…...
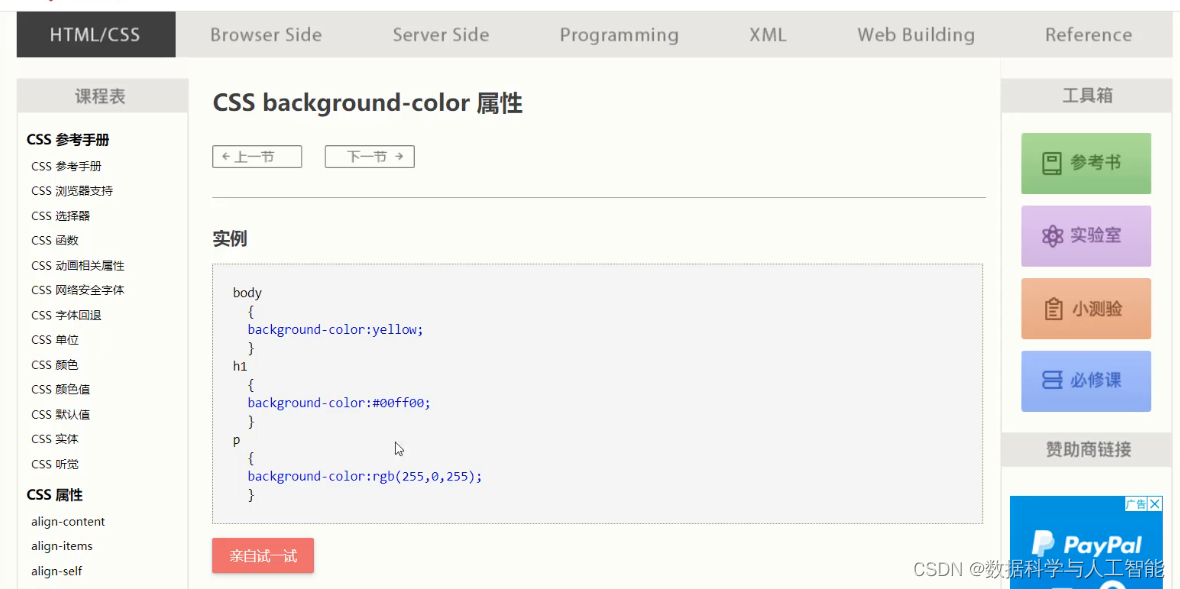
HTMLCSS
1、HTML 1.1 介绍 HTML 是一门语言,所有的网页都是用HTML 这门语言编写出来的,也就是HTML是用来写网页的,像京东,12306等网站有很多网页。 这些都是网页展示出来的效果。而HTML也有专业的解释 HTML(HyperText Markup Language)…...

【安装Nginx】
Linux上安装Nginx 文章目录 Linux上安装NginxUbuntuCentOS查看已安装的软件 Ubuntu 在 Ubuntu 上安装 Nginx 非常简单。只需按照以下步骤操作: 打开终端,更新软件包索引: sudo apt update安装 Nginx: sudo apt install nginx安…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
