盲目自学网络安全只会成为脚本小子?
前言:我们来看看怎么学才不会成为脚本小子
目录:
- 一,怎么入门?
-
- 1、Web 安全相关概念(2 周)
- 2、熟悉渗透相关工具(3 周)
- 3、渗透实战操作(5 周)
- 4、关注安全圈动态(1 周)
- 5、熟悉 Windows/Kali Linux(3 周)
- 6、服务器安全配置(3 周)
- 7、脚本编程学习(4 周)
- 8、源码审计与漏洞分析(3 周)
- 9、安全体系设计与开发(5 周)
- 二,我的学习心得,我认为能不能自学成功
一,怎么入门?
1、Web 安全相关概念(2 周)
-
了解网络安全相关法律法规
-
熟悉基本概念(SQL 注入、上传、XSS、CSRF、一句话木马等)。
-
通过关键字(SQL 注入、上传、XSS、CSRF、一句话木马等)进行 Google;
-
阅读《精通脚本黑客》,虽然很旧也有错误,但是入门还是可以的;
-
看一些渗透笔记/视频,了解渗透实战的整个过程,可以 Google(渗透笔记、渗透过程、入侵过程等);
2、熟悉渗透相关工具(3 周)
-
熟悉 AWVS、sqlmap、Burp、nessus、chopper、nmap、Appscan 等相关工具的使用。
-
了解该类工具的用途和使用场景,先用软件名字 Google;
-
下载无后门版的这些软件进行安装;学习并进行使用,例如:Brup 的教程、sqlmap;待常用的这几个软件都学会了可以安装音速启动做一个渗透工具箱;
3、渗透实战操作(5 周)
-
掌握渗透的整个阶段并能够独立渗透小型站点。网上找渗透视频看并思考其中的思路和原理,关键字(渗透、SQL 注入视频、文件上传入侵、数据库备份、dedecms 漏洞利用等等);
-
自己找站点/搭建测试环境进行测试,记住请隐藏好你自己;
-
思考渗透主要分为几个阶段,每个阶段需要做那些工作;
-
研究 SQL 注入的种类、注入原理、手动注入技巧;研究文件上传的原理,如何进行截断、双重后缀欺骗(IIS、PHP)、解析漏洞利用(IIS、Nignix、Apache)等;
-
研究 XSS 形成的原理和种类,具体学习方法可以 Google;研究 Windows/Linux 提权的方法和具体使用;
4、关注安全圈动态(1 周)
-
关注安全圈的最新漏洞、安全事件与技术文章。
-
浏览每日的安全技术文章/事件;
-
通过 Weibo/twitter 关注安全圈的从业人员(遇到大牛的关注或者好友果断关注),天天抽时间刷一下
-
通过 feedly/鲜果订阅国内外安全技术博客(不要仅限于国内,平时多注意积累);
-
多关注下最新漏洞列表,推荐几个:exploit-db
5、熟悉 Windows/Kali Linux(3 周)
-
学习 Windows/Kali Linux 基本命令、常用工具;
-
熟悉 Windows 下的常用的 cmd 命令,例如:ipconfig,nslookup,tracert,net,tasklist,taskkill 等;
-
熟悉 Linux 下的常用命令,例如:ifconfig,ls,cp,mv,vi,wget,service,sudo 等;
-
熟悉 Kali Linux 系统下的常用工具,可以参考 SecWiki,《Web Penetration Testing with Kali Linux》、《Hacking with Kali》等;
-
熟悉 metasploit 工具,可以参考 SecWiki、《Metasploit 渗透测试指南》。
6、服务器安全配置(3 周)
学习服务器环境配置,并能通过思考发现配置存在的安全问题。Windows2003/2008 环境下的 IIS 配置,特别注意配置安全和运行权限,;Linux 环境下的 LAMP 的安全配置,主要考虑运行权限、跨目录、文件夹权限等;远程系统加固,限制用户名和口令登陆,通过 iptables 限制端口;配置软件 Waf 加强系统安全,在服务器配置 mod_security 等系统;通过 Nessus 软件对配置环境进行安全检测,发现未知安全威胁。
7、脚本编程学习(4 周)
选择脚本语言 Perl/Python/PHP/Go/Java 中的一种,对常用库进行编程学习。搭建开发环境和选择 IDE,PHP 环境推荐 Wamp 和 XAMPP,IDE 强烈推荐 Sublime;Python 编程学习,学习内容包含:语法、正则、文件、网络、多线程等常用库,推荐《Python 核心编程》,不要看完;用 Python 编写漏洞的 exp,然后写一个简单的网络爬虫;PHP 基本语法学习并书写一个简单的博客系统
8、源码审计与漏洞分析(3 周)
能独立分析脚本源码程序并发现安全问题。熟悉源码审计的动态和静态方法,并知道如何去分析程序;从 Wooyun 上寻找开源程序的漏洞进行分析并试着自己分析;了解 Web 漏洞的形成原因,然后通过关键字进行查找分析;研究 Web 漏洞形成原理和如何从源码层面避免该类漏洞,并整理成 checklist。
9、安全体系设计与开发(5 周)
能建立自己的安全体系,并能提出一些安全建议或者系统架构。开发一些实用的安全小工具并开源,体现个人实力;建立自己的安全体系,对公司安全有自己的一些认识和见解;提出或者加入大型安全系统的架构或者开发;
这个 Web 安全学习路线,整体大概半年左右,具体视每个人的情况而定。

(上传一直很模糊,所以就没有展开了,需要高清版的可以在下面领取)
👉网络安全&黑客&渗透学习大礼包
如果你把每周要学的内容精细化到这种程度,你还会担心学不会,入不了门吗,其实说到底就是学了两个月,但都是东学一下,西学一下,什么内容都是浅尝辄止,没有深入进去,所以才会有学了 2 个月,入不了门这种感受。
这个路线图已经详细到每周要学什么内容,学到什么程度,可以说我整理的这个 Web 安全路线图对新人是非常友好的,除此之外,我还给小伙伴整理了相对应的学习资料,如果你需要的话,我也可以分享一部分出来(涉密部分分享不了),需要的可以点击蓝色字获取
👉网络安全&黑客&渗透学习大礼包

除了有视频教程,同时也为大家整理了各种文档和书籍资料
二,我的学习心得,我认为能不能自学成功的要素有两点。
第一点就是自身的问题,虽然想要转行学习安全的人很多,但是非常强烈的想要转行学好的人是小部分。而大部分人只是抱着试试的心态来学习安全,这是完全不可能的。
所以能不能学成并且就业,最关键的一点就是自己的愿望是否强烈。我是属于非常强烈那种,因为忍受不了现在工作的氛围,以及羡慕朋友在北京可以拿到 3 万的月薪,这些因素都促使我非常拼命的学。
在加上自身可以做到从下班就开始看视频自学,一直学到晚上 12 点的这股劲,所以才能在 5 个月的时间内达到就业的水平。第二点就是有大佬带你,如果全程都靠自己摸索是非常难的,对于一个不是本专业的人来说从开始的时候就“无从下手”。
更不要说在学习过程中遇到的无数 bug 问题很难得到解决,因为我们在学习过程中会遇到无数问题,有的时候一个小问题就能困扰我们几个小时的时间,会导致我们的学习效率很低,这种情况出现多了以后,信心就会受到打击,觉得自己不适合学这行,最终放弃。
而当有一个大佬去给你解答后,你会很快得到答案,并且能理解为什么要这样做,到底是哪里出现了问题,学习效率会非常高。所以总结就是自身自觉主动学习再加上大佬全程带你,其实学习就是这么简单的事情,无非就是这两个关键的要素,少了其中一个都很难成功。
相关文章:

盲目自学网络安全只会成为脚本小子?
前言:我们来看看怎么学才不会成为脚本小子 目录: 一,怎么入门? 1、Web 安全相关概念(2 周)2、熟悉渗透相关工具(3 周)3、渗透实战操作(5 周)4、关注安全圈动…...

文从字顺|程序员须知,如何编写高质量代码
高质量代码是软件开发中至关重要的一部分。高质量的代码不仅可以提高软件的可维护性和可复用性,还可以增强软件的安全性和稳定性。同时,可以降低软件维护成本,提升开发效率,为用户提供更好的使用体验。 写出高质量代码是每个程序…...
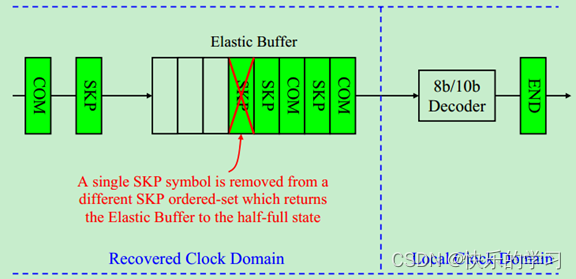
PCIe物理层弹性缓存机制(详细)解析-PCIe专题知识(四)
目录 前言一、简介二、详细解析2.1 实例解析2.2 具体实现过程 三、总结四、其他相关链接1、PCI总线及发展历程总结2、PCIe物理层总结-PCIE专题知识(一)3、PCIe数据链路层图文总结-PCIe专题知识(二)4、PCIe物理层链路训练和初始化总…...

分片上传和断点续传的区别?实现思路是什么?
相同: 分片上传和断点续传都是网络传输中常用的重要技术 不同: 分片上传:将一个大文件切分为多个小文件进行上传。这种方式能够加快上传速度,降低服务器压力,特别适用于大型文件的上传。例如,在云存储系统…...
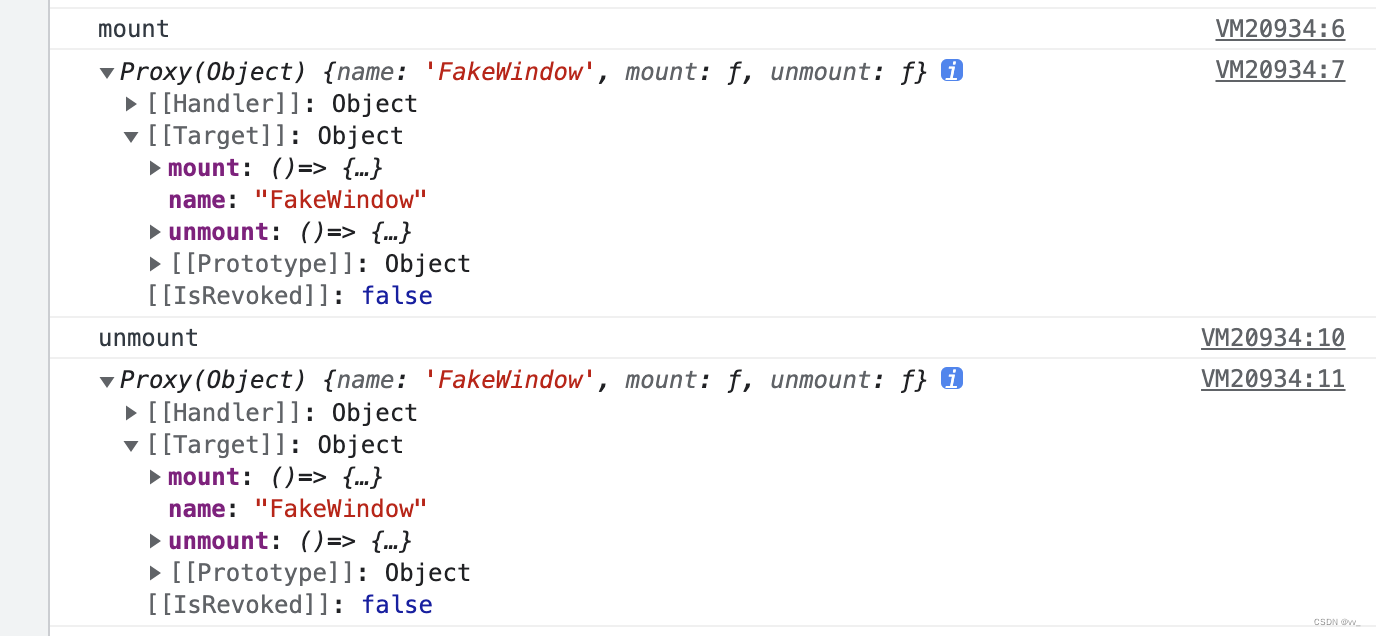
微前端 qiankun@2.10.5 源码分析(二)
微前端 qiankun2.10.5 源码分析(二) 我们继续上一节的内容。 loadApp 方法 找到 src/loader.ts 文件的第 244 行: export async function loadApp<T extends ObjectType>(app: LoadableApp<T>,configuration: FrameworkConfi…...

08异步请求:何种场景下应该使用异步请求?
异步在计算机科学中早就是一个比较常用的词汇,从操作系统的特性( 并发、共享、虚拟、异步)开始,异步就在处理并发操作中起到很大的作用,不仅如此,在软件层面,异步同样也是解决并发请求的一个关键过程,它可以将瞬时激增的请求进行更加灵活的处理,通过异步请求,客户端可…...

【深度学习 | Transformer】Transformers 教程:pipeline一键预测
文章目录 一、前言二、Computer vision2.1 Image classification2.2 Object detection2.3 Image segmentation2.4 Depth estimation 三、NLP3.1 Text classification3.2 Token classification3.3 Question answering3.4 Summarization3.5 Translation3.6 Language modeling3.6.…...
HTMLCSS
1、HTML 1.1 介绍 HTML 是一门语言,所有的网页都是用HTML 这门语言编写出来的,也就是HTML是用来写网页的,像京东,12306等网站有很多网页。 这些都是网页展示出来的效果。而HTML也有专业的解释 HTML(HyperText Markup Language)…...

【安装Nginx】
Linux上安装Nginx 文章目录 Linux上安装NginxUbuntuCentOS查看已安装的软件 Ubuntu 在 Ubuntu 上安装 Nginx 非常简单。只需按照以下步骤操作: 打开终端,更新软件包索引: sudo apt update安装 Nginx: sudo apt install nginx安…...

VSCode作业1:猜数字游戏和简单计数器(包含完整代码)
目录 猜数字游戏 一、使用‘random’函数获取随机数 二、 分情况讨论输入值大小情况 三、HTML代码 四、CSS样式及运行效果 简单计数器(计时器) 一、使用‘setInterval’函数实现计数效果 二、使用’clearInterval‘函数实现暂停计数和重新计数效果 …...

NANK OE骨传导开放式蓝牙耳机发布,极致体验拉满!
近日,中国专业音频品牌NANK南卡发布了全新一代——骨传导开放式蓝牙耳机NANK OE,耳机采用了传统真无线和骨传导的结合方式,带来更加舒适的佩戴体验和音质升级,同时还支持单双耳自由切换,全新的设计收获了市场的喜爱和认…...
看完这篇文章你就彻底懂啦{保姆级讲解}-----(I.MX6U驱动GPIO中断《包括时钟讲解》) 2023.5.9
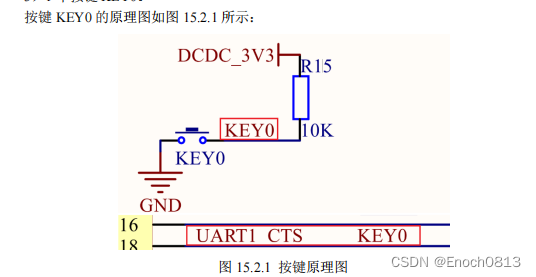
目录 前言整体文件结构源码分析(保姆级讲解)中断初始化部分初始化GIC控制器初始化中断向量表设置中断向量表偏移 系统时钟初始化部分使能所有的时钟部分led初始化部分beep初始化部分key初始化部分按键中断初始化部分按键中断服务函数部分 while循环部分 …...
MySql -- 事务
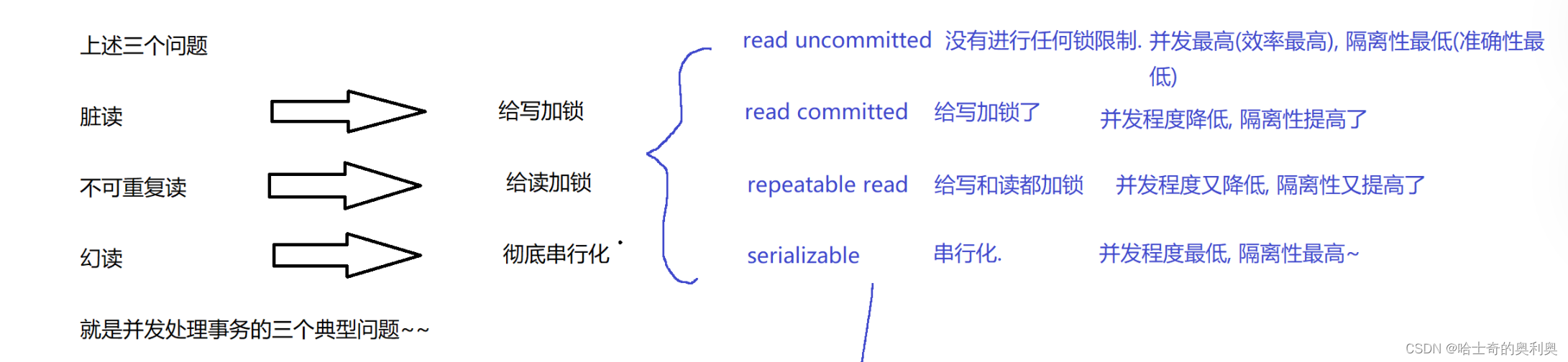
目录 1.概念 2.事务的运用场景 3.事务的四大特点 4.执行事务带来的问题 4.1 脏读 4.2 不可重复度 4.3 幻读 5. MySQL中事务的隔离级别 1.概念 事务就是把若干个独立操作打包成一个整体而诞生的一种功能. 2.事务的运用场景 比如:A——>B 转账500 A的余额-500…...

关于大模型对未来影响的一点看法
人们总是高估了未来一到两年的变化,低估了未来十年的变革。 ---比尔盖茨 近来OpenAI的GPT技术可以说在全球都带来了巨大的影响,也让大家看到了什么叫大力出奇迹。chatGPT和GPT4的能力给了大家很大的震撼,其流畅自如、逻辑清晰、出众的能力&am…...

Android - 约束布局 ConstraintLayout
一、概念 解决布局嵌套过多的问题,采用方向约束的方式对控件进行定位。 二、位置约束 2.1 位置 至少要保证水平和垂直方向都至少有一个约束才能确定控件的位置。 layout_constraintLeft_toLeftOf我的左边,与XXX左边对齐。layout_constraintLeft_toRight…...

Addictive Multiplicative in NN
特征交叉是特征工程中的重要环节,在以表格型(或结构化)数据为输入的建模中起到了很关键的作用。 特征交互的作用,一是尽可能挖掘对目标有效的模式、特征,二是具有较好的可解释性,三是能够将对数据的洞见引…...
LeetCode 1206. 实现跳表
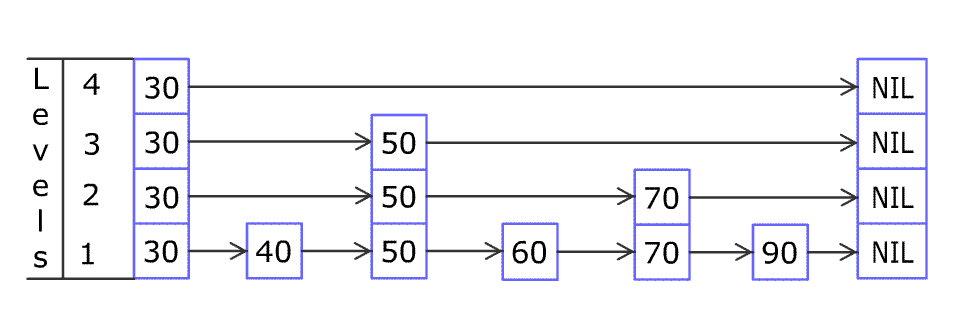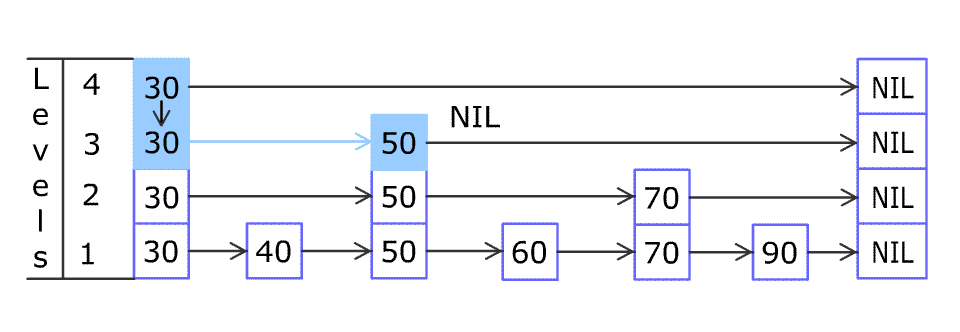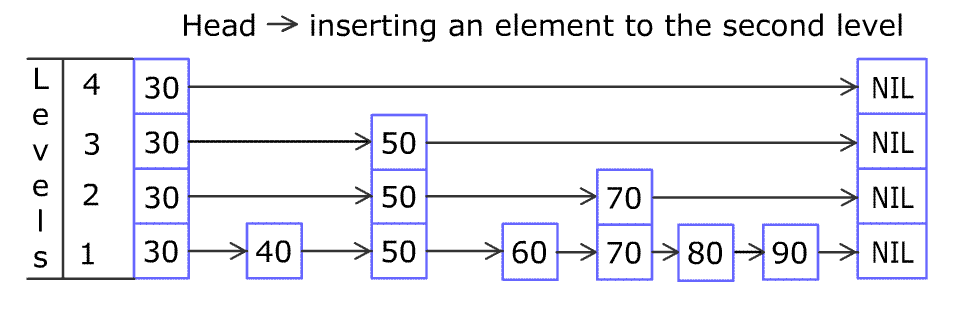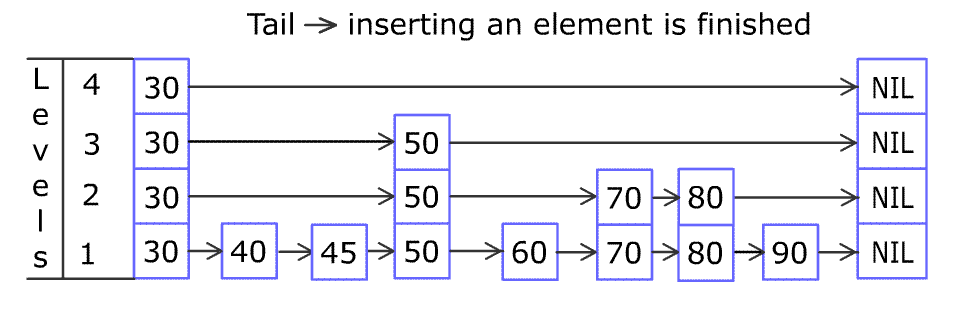
不使用任何库函数,设计一个跳表。 跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。 例如,一个跳表包…...
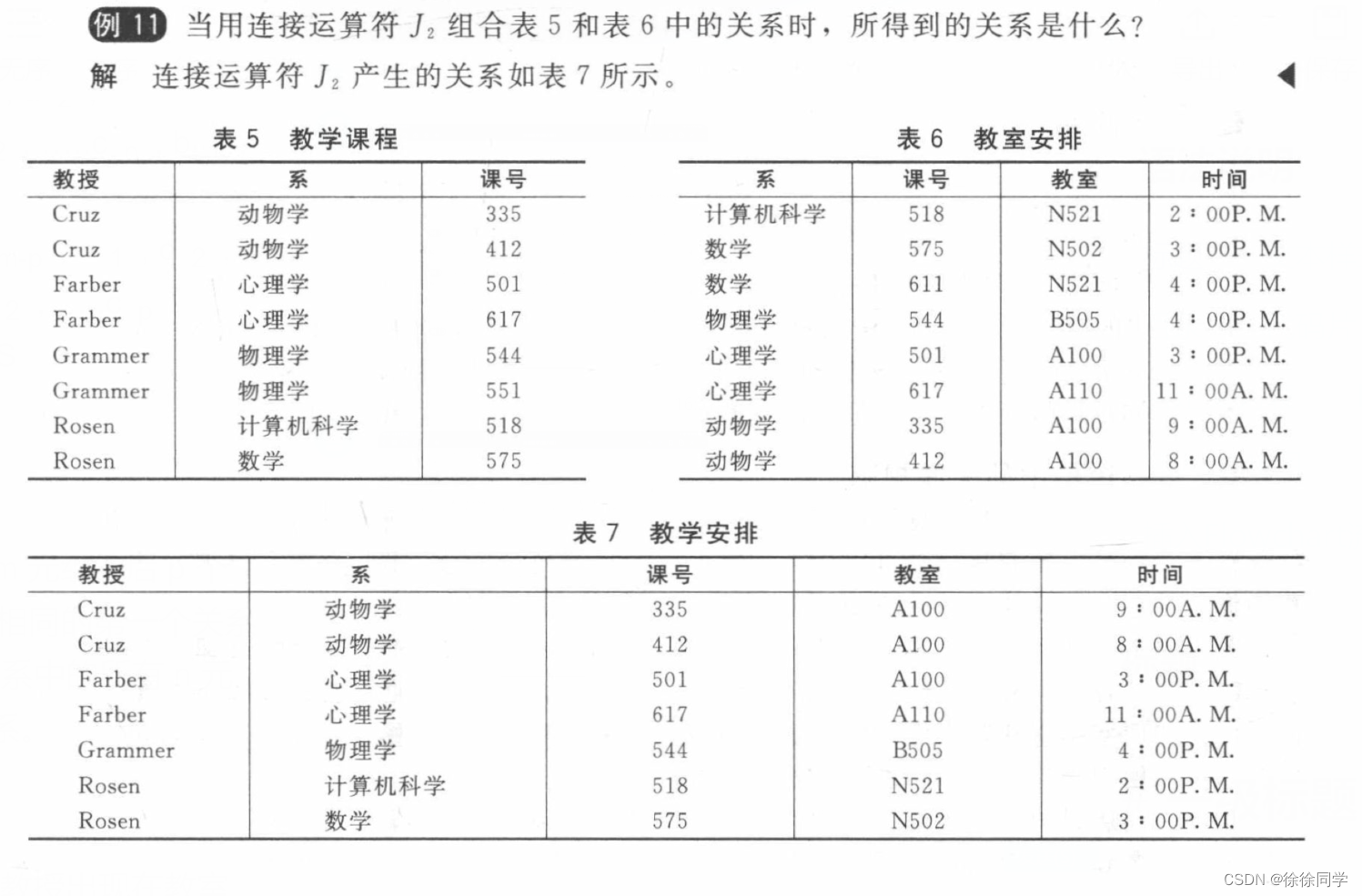
离散数学_九章:关系(2)
9.2 n元关系及其应用 1、n元关系,关系的域,关系的阶2、数据库和关系 1. 数据库 2. 主键 3. 复合主键 3、n元关系的运算 1. 选择运算 (Select) 2. 投影运算 (Project) 3. 连接运算 (Join) n元关系:两个以上集合的元素间的关系 1、n元关系…...

[ubuntu][原创]通过apt方式去安装libnccl库
ubuntu18.04版本安装流程: wget https://developer.download.nvidia.com/compute/cuda/repos/ubuntu1804/x86_64/cuda-ubuntu1804.pin sudo mv cuda-ubuntu1804.pin /etc/apt/preferences.d/cuda-repository-pin-600 sudo apt-key adv --fetch-keys https://develo…...

YonLinker连接集成平台构建新一代产业互联根基
近日,由用友公司主办的“2023用友BIP技术大会“在用友产业园(北京)盛大召开,用友介绍了更懂企业业务的用友BIP-iuap平台,并发布了全面数智化能力体系,助力企业升级数智化底座,加强加速数智化推进…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
