蓝桥:前端开发笔面必刷题——Day1 数组(一)
文章目录
- 📋前言
- 🎯数组中重复的数字
- 📚题目内容
- ✅解答
- 🎯两数之和
- 📚题目内容
- ✅解答
- 🎯替换空格
- 📚题目内容
- ✅解答
- 🎯二维数组中的查找
- 📚题目内容
- ✅解答
- 📝最后

📋前言
这个系列的文章收纳的内容是来自于蓝桥云课的前端岗位笔面必刷题的内容,简介是:30天133题,本题单题目全部来自于近2年BAT等大厂前端笔面真题!因为部分题目是需要会员,所以该系列的文章内容并非完全全面(如果需要会员的题目,则从 leetcode 补充对应的题目,题目大概也是一样的考法)。文章中题目涉及的内容包括原题、答案和解析等等。
🎯数组中重复的数字
📚题目内容
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0 ~ n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
输入:[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
题目给的测试用例里有以下限制:
2 <= n <= 14。
✅解答
初始提供代码
function findRepeatNumber(nums) {// 补充代码
}
答案
function findRepeatNumber(nums) {let hash = new Set()for(let i=0;i<nums.length;i++){if(hash.has(nums[i])){return nums[i]}hash.add(nums[i])}
}
函数 findRepeatNumber 接收一个数组 nums,并返回一个重复的数字。在循环中,我们使用 Set 的 has 方法来判断当前数字是否已经出现过,如果是,则直接返回该数字;否则,将该数字添加到 Set 中。
该算法的时间复杂度为 O(n),空间复杂度为 O(n)。
🎯两数之和
📚题目内容
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
输入: nums = [2,7,11,15], target = 9
输出: [0,1]
解释: 因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
输入: nums = [3,2,4], target = 6
输出: [1,2]
输入: nums = [3,3], target = 6
输出: [0,1]
题目给的测试用例里有以下限制:
2 <= nums.length <= 4。2 <= nums[i] <= 11。6 <= target <= 10。- 只会存在一个有效答案。
✅解答
初始提供代码
function twoSum(nums, target) {// 补充代码
}
答案
function twoSum(nums, target) {for(let i=0;i<nums.length;i++){for(let j=i+1;j<nums.length;j++){if(nums[i]+nums[j]===target){return [i,j]}}}
}
采用双 for 循环,暴力枚举的思想来实现。首先使用两个嵌套的循环来遍历整个 nums 数组,对于每对不同的下标 i 和 j(i < j),计算它们所对应的数之和,并判断是否等于目标值 target。如果相等,则直接返回这两个下标。
该函数的时间复杂度为 O(n^2),因为需要进行两层循环嵌套,最多需要遍历 n(n-1)/2 个数对。空间复杂度为 O(1),因为只需要使用常数个变量来存储结果。
另一种解法
function twoSum(nums, target) {const hashmap = new Map();for (let i = 0; i < nums.length; i++) {const num2 = target - nums[i];if (hashmap.has(num2)) {return [hashmap.get(num2), i];}hashmap.set(nums[i], i);}
}
该函数的实现中,首先创建了一个新的 Map 对象 hashmap,然后遍历整个 nums 数组。对于每个数字 nums[i],计算出与目标值之差 num2 = target - nums[i],然后在 hashmap 中查找是否存在满足条件的 num2,如果存在,则直接返回对应的下标;如果不存在,则将当前数字作为新的键,将下标作为对应的值,存储到 hashmap 中,以备下次查找时使用。
该算法的时间复杂度为 O(n),空间复杂度为 O(n)。
🎯替换空格
📚题目内容
请实现一个函数,把字符串 s 中的每个空格替换成 “%20”。
题目给的测试用例里有以下限制:
0 <= s.length <= 14。
✅解答
初始提供代码
function replaceSpace(s) {// 补充代码。
}
答案
function replaceSpace(s) {let result = "";for (let i = 0; i < s.length; i++) {if (s[i] === " ") {result += "%20"} else {result += s[i]}}return result
}
首先创建一个新的空字符串 result,然后遍历原始字符串 s 中的每个字符。对于每个字符,如果它是一个空格,则将 "%20" 添加到 result 中,否则直接将它添加到 result 中。
该函数的时间复杂度为 O(n),其中 n 是原始字符串 s 的长度,因为需要遍历一遍输入的字符串。而空间复杂度也为 O(n),因为最坏情况下,需要将每个空格都替换为 "%20"。
另一种解法
function replaceSpace (s) {return s.replace(/\s/g,'%20')
}
使用 String 类型的 replace 方法和正则表达式对字符串 s 进行替换空格的处理,在这个实现中,我们通过正则表达式 /\s/g 匹配所有空格字符,并使用 "%20" 作为新的内容来替换它们。最终返回替换后的字符串即可。
该函数的时间复杂度同样为 O(n),其中 n 是原始字符串 s 的长度,因为需要遍历一遍输入的字符串并进行替换操作。而空间复杂度也为 O(n),因为在正则表达式匹配后会得到一个新的字符串对象,并且该字符串对象的长度可能比原始字符串更长,因此需要额外的空间来存储。
🎯二维数组中的查找
📚题目内容
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。示例:
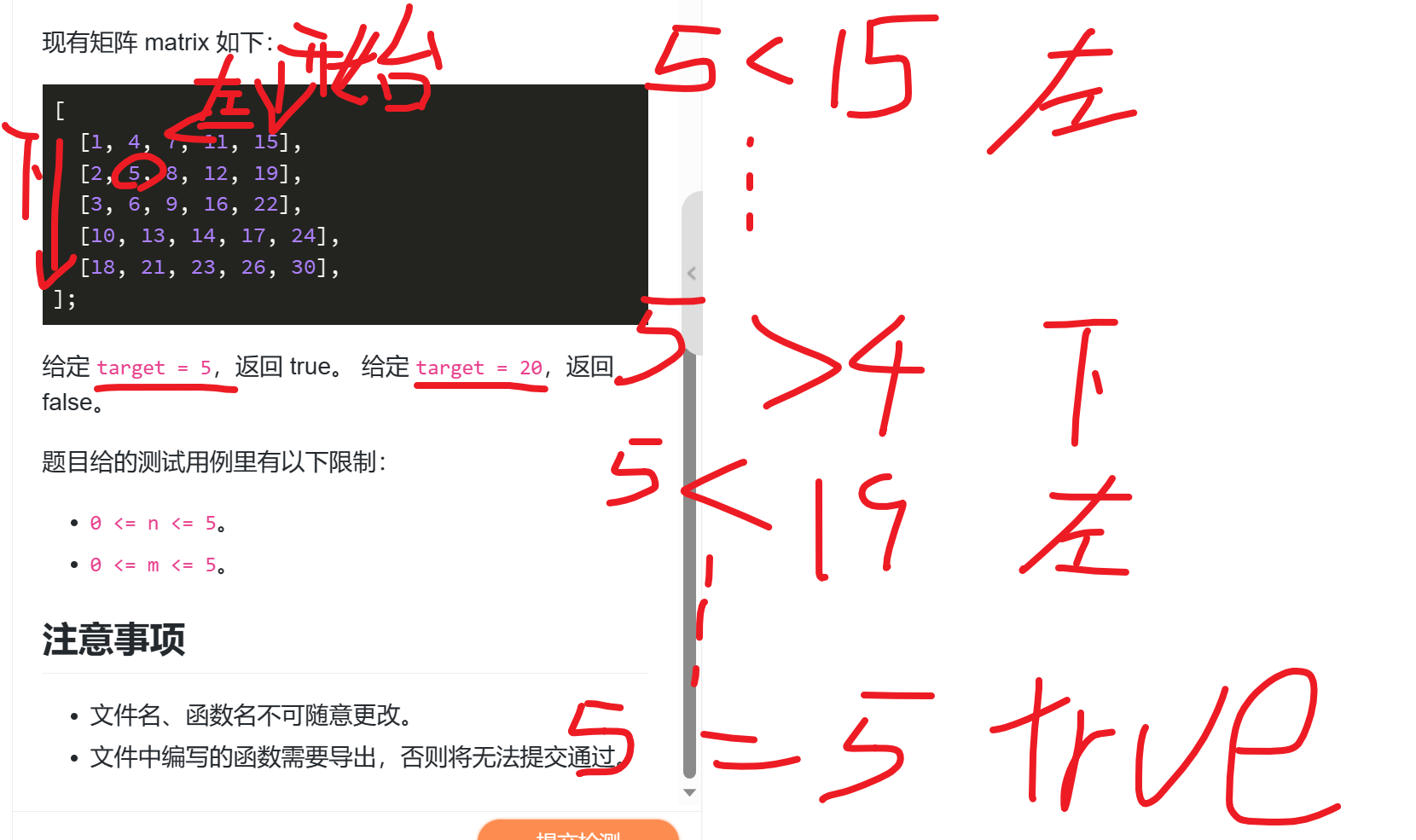
现有矩阵 matrix 如下:
[[1, 4, 7, 11, 15],[2, 5, 8, 12, 19],[3, 6, 9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30],
];
给定 target = 5,返回 true。 给定 target = 20,返回 false。
题目给的测试用例里有以下限制:
0 <= n <= 5。0 <= m <= 5。。
✅解答
初始提供代码
function findNumberIn2DArray(matrix, target) {// 补充代码。
}
答案
function findNumberIn2DArray(matrix, target) {if (!matrix || matrix.length === 0 || matrix[0].length === 0) {return false;}const m = matrix.length; // 行数const n = matrix[0].length; // 列数let row = 0; // 行指针,从第一行开始let col = n - 1; // 列指针,从最后一列开始while (row < m && col >= 0) {if (matrix[row][col] === target) { // 找到了目标值return true;} else if (matrix[row][col] > target) { // 当前值比目标值大,向左移动列指针col--;} else { // 当前值比目标值小,向下移动行指针row++;}}return false; // 遍历完整个数组都没有找到目标值
}
该函数的实现中,首先通过检查输入矩阵是否为空来判断是否需要提前返回 false。然后,定义了两个指针 row 和 col ,分别用于表示当前搜索的行和列。由于矩阵中的每一行都已经按照升序排列,而每一列也已经按照升序排列,因此可以采用类似于二分查找的方法进行搜索。
具体来说,在每次迭代中,我们比较当前指针所在位置的元素与目标值的大小关系。我们可以从矩阵的右上角开始搜索,如果当前值等于 target,则直接返回 true 。如果当前值大于 target,则说明 target 可能出现在当前元素的左侧,因此需要将列指针向左移动一位 。反之,如果当前值小于 target ,则说明目标值可能出现在当前元素的下方,因此需要将行指针向下移动一位 。不断重复以上步骤,直到找到目标值或者搜索完整个数组。
该函数的时间复杂度为 O(m+n),其中 m 和 n 分别表示矩阵的行数和列数。因为每次迭代可以将搜索范围缩小一行或者一列,最多需要进行 m+n 次迭代才能找到目标值(当目标值位于矩阵的右上角时)。而空间复杂度为 O(1),因为只使用了常数级别的额外空间来存储指针和一些临时变量。
📝最后
感谢阅读到这,这就是 Day1 的全部内容了,文章内容中题目的答案都是通过检测的了,如果有疑问和争议的内容,可以评论区留言和私信我,收到消息第一时间解答和回复。

相关文章:

蓝桥:前端开发笔面必刷题——Day1 数组(一)
文章目录 📋前言🎯数组中重复的数字📚题目内容✅解答 🎯两数之和📚题目内容✅解答 🎯替换空格📚题目内容✅解答 🎯二维数组中的查找📚题目内容✅解答 📝最后 …...

SQL 教程-入门基础篇
文章目录 SQL 简介SQL 语法SQL SELECT 语句SQL SELECT DISTINCT 语句SQL WHERE 子句SQL AND & OR 运算符SQL ORDER BY 关键字SQL INSERT INTO 语句SQL UPDATE 语句SQL DELETE 语句 SQL 简介 SQL(Structured Query Language)是一种用于管理和操作关系…...
——信号的循环平稳性(循环自相关函数)原理及推导)
循环自相关函数和谱相关密度(六)——信号的循环平稳性(循环自相关函数)原理及推导
在通信、遥测、雷达和声纳系统中,一些人工信号是一类特殊的非平稳信号,它们的非平稳性表现为周期平稳性。通信信号常用待传输信号对周期性信号的某个参数进行调制、如对正弦载波进行调幅、调频和调相,以及对周期性脉冲信号进行脉幅、脉宽和脉位调制,都会产生具有周期平稳性…...

C/C++:04. 多态和虚函数
不加virtual,只能访问成员变量,不能访问成员函数 文章目录 前言1 虚函数与多态不用虚函数的多态使用虚函数的多态 2 C虚函数注意事项 构成多态的条件C虚函数注意事项构成多态的条件什么时候声明虚函数 3 C虚析构函数的必要性总结 前言 本节阐述C中的多态…...

拿下多个定点/比亚迪要上!这项技术要「降维打击」单目感知
2008年,斯巴鲁在全球首次推出了搭载有立体视觉摄像头的主动安全解决方案,并具有紧急制动功能的“EyeSight”。2010年,斯巴鲁推出升级版的“EyeSight”,成为世界上首个可以在全车速范围内避免碰撞的量产技术系统。 2014年ÿ…...

Go 的时间操作
Go 的时间操作 1. time 包 1.1. 时间类型 Go 语言中时间类型有两种: time.Time:表示时间的类型,常见的有两种方式: time.Now():获取当前的时间time.Date():根据指定的年、月、日、时、分、秒、纳秒等创…...

ThreeJS进阶之矩阵变换
ThreeJS的矩阵变换 Three.js使用matrix编码3D变换 —— 平移(位置),旋转和缩放。Object3D的每个实例都有一个matrix,用于存储该对象的位置,旋转和比例。这里介绍如何更新对象的变换。 三维物体(Object3D) 这是Three.js中大部分对象的基类,提供了一系列的属性和方法来对…...

分布式锁概念
什么是分布式锁 方案一:SETNX EXPIRE 方案二:SETNX value值是(系统时间过期时间) 方案三:使用Lua脚本(包含SETNX EXPIRE两条指令) 方案四:SET的扩展命令(SET EX PX NX) 方案五…...

PMP课堂模拟题目及解析(第10期)
91. 在项目执行阶段,一名项目干系人要求项目经理加入一个新过程的优化。项目经理应该怎么做? A. 执行实施整体变更控制过程。 B. 与过程专家一起审查项目。 C. 将优化项目分配给团队。 D. 拒绝范围蔓延企图。 92. 项目经理要求团队提供对项目应急计…...

Arm微架构分析系列3——Arm的X计划
1. 引言 前文介绍了Arm公司近几年在移动处理器市场推出的Cortex-A系列处理器。Cortex-A系列处理器每年迭代,性能和能效不断提升,是一款非常成功的产品。但是,Arm并不满足于Cortex-A系列每年的架构小幅度升级,又推出了X计划&#x…...
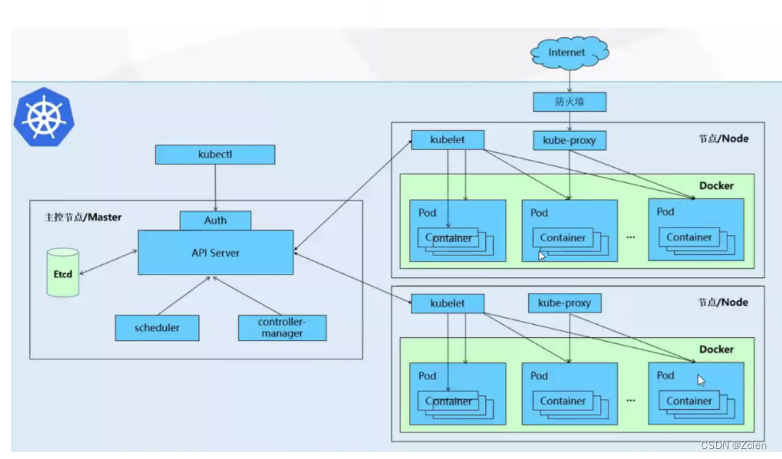
Kubernetes(K8S)的基础概念
文章目录 一、Kubernetes介绍1、什么是Kubernetes?2、为什么要用K8S?3、k8s的特性 二、k8s集群架构与组件1、Master组件2、配置存储中心——etcd3、Worker Node 组件 三、k8s核心概念●Pod●Pod 控制器(五大控制器)●Label●Label选择器(Label selector )●Service…...
)
【Linux进阶命令 04】lsof (看看是谁动了我的文件?)
文章目录 一、简介二、lsof语法2.1 基本格式2.2 选项2.3 输出字段解释 三、常用 lsof 操作3.1 查看某文件的相关进程3.2 网络相关:-i3.3 指定进程号打开的文件:-p3.4 指定用户打开的文件:-u3.5 某进程打开的文件:-c3.6 复合查询 四…...

华为OD机试真题 Java 实现【数字加减游戏】【2023Q1 200分】
一、题目描述 小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字s变成数字t。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减,分别为a,其中b没有使用次数限制。 请问小明…...
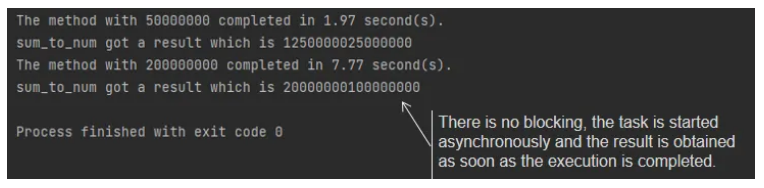
Python: 结合多进程和 Asyncio 以提高性能
动动发财的小手,点个赞吧! 简介 多亏了 GIL,使用多个线程来执行 CPU 密集型任务从来都不是一种选择。随着多核 CPU 的普及,Python 提供了一种多处理解决方案来执行 CPU 密集型任务。但是直到现在,直接使用多进程相关的…...

只需要两步就能快速接入GPT
缘起 最近一个朋友提出,让我出个关于如何快速接入GPT的教程,今天就给大家安排上。 需要的工具 经过实测,这是迄今为止最便捷的接入方式,而且亲测有效。 首先,第一步你需要下载最新版的微软Edge浏览器,去…...
使用Git-lfs上传超过100m的大文件到GitHub
文章目录 1. 安装 git-lfs2. 在Git中安装git-ifs3. 找到工程中的所有大文件4.执行完这行命令,项目目录下会生成文件 .gitattributes,此时Git push将 .gitattributes 提交到远程仓库。 5. 需要注意的事 1. 安装 git-lfs Git Large File Storage | Git La…...

【网络】计算机中的网络
目录 🍁计算机网络 🍁计算机网络模型 🍁布线工程 🍁布线系统 🦐博客主页:大虾好吃吗的博客 🦐专栏地址:网络专栏 计算机网络 计算机网络的功能 数据通信、资源共享、增加可靠性、提…...

什么是语音识别的语音助手?
前言 语音助手已经成为现代生活中不可或缺的一部分。人们可以通过语音助手进行各种操作,如查询天气、播放音乐、发送短信等。语音助手的核心技术是语音识别。本文将详细介绍语音识别的语音助手。 语音识别的基本原理 语音识别是将语音信号转换为文本的技术。语音识…...

自己动手写一个加载器
前言 当在 linux 命令行中 ./ 运行一个程序时,实际上操作系统会调用加载器将这个程序加载到内存中去执行。为了探究加载器的行为,今天我们就自己动手写一个简单的加载器。 工作原理 加载器的工作原理: 从磁盘读取 bin 文件到内存…...

C# 性能优化和Unity性能优化
C# 性能优化 C# 性能优化是一个非常广泛的话题,需要从各个方面来考虑,包括算法和数据结构、编译器优化、代码优化等等。下面是一些常见的 C# 性能优化技巧: 选择正确的数据结构:C# 提供了各种不同的数据结构,例如数组、…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
