量化投资 无套利 No-arbitrage
文章目录
- 量化投资 无套利 No-arbitrage
- State of Nature
- 市场域 Market Span
- 套利 Arbitrage
- 无套利和正线性定价规则 No-arbitrage and Positive Linear Pricing Rule
- Implication 1: One-price Principle
- Implication 2: Positivity
- Implication 3: Additivity
- Implication 4: Homogeneity
- Implication 5: Recursivity
- Implication 6: Risk-neutral Pricing Rule
- Implication 7: Risk-free Return Rule
- The Fundamental Theorem
- 二叉树期权定价模型
- 单期期权定价模型 A Signle-period Model
- 二叉树期权定价模型 CRR Binomial Model
- 倒向过程 Backward Procedure
- 带有常数红利的期权定价 Option Pricing with Constant Dividend Yield
- 美式期权定价问题
量化投资 无套利 No-arbitrage
State of Nature
经济主体所面临的不确定性是关于在状态空间 Ω \Omega Ω 中对自然状态的实现:
① Ω = { ω 1 , ω 2 . ⋯ , ω S } \Omega=\{\omega_1,\,\omega_2.\,\cdots,\,\omega_S\} Ω={ω1,ω2.⋯,ωS} 是全体的状态空间;
② T = { 0 , ⋯ , T } \bold{T}=\{0,\,\cdots,\,T\} T={0,⋯,T} 代表交易时间;
③ F t \bold{F}_t Ft 代表时刻 t t t 的信息:对于每一个状态 ω \omega ω , F t ( ω ) \bold{F}_t(\omega) Ft(ω) 代表当 t t t 时刻的状态为 ω \omega ω 时,我们所得到的所有信息(或者说剩下的无法排除的状态)。我们假设:
F 0 ( ω ) = Ω , F t ( ω ) ⊆ F s ( ω ) for s ≤ t \bold{F}_0(\omega)=\Omega,\quad\bold{F}_t(\omega)\subseteq \bold{F}_s(\omega)\,\,\text{for}\,\,s\leq t F0(ω)=Ω,Ft(ω)⊆Fs(ω)fors≤t
④ P \bold{P} P 是状态空间上的概率测度。
市场域 Market Span
我们有 J J J 支可交易证券,他们分别由他们的未来现金流所定义,并且 adapt to 事件空间 ( Ω , F t , P ) (\Omega,\,\bold{F}_t,\,\bold{P}) (Ω,Ft,P) 。(这句话我不知道怎么翻译,可以看一下原文:)
Securities are identified respectively with their future cash flows adapted to the event space ( Ω , F t , P ) (\Omega,\,\bold{F}_t,\,\bold{P}) (Ω,Ft,P)
(老师上课强调了 adapt to 和其他措辞的区别,但是我没有听懂。。。)
① 现金流(红利)dividend: { δ t } t = 1 T \{ \delta_t\}_{t=1}^{T} {δt}t=1T ,其中 δ t ≡ [ δ t 1 , ⋯ , δ t J ] \delta_t \equiv \left[\delta_t^1,\,\cdots,\,\delta_t^J\right] δt≡[δt1,⋯,δtJ] , δ t j \delta_t^j δtj 是证券 j j j 在时刻 t t t 的现金流;
② 证券价格 Security prices: { p t } t = 0 T \{p_t\}_{t=0}^{T} {pt}t=0T , p t ≡ [ p t 1 , ⋯ , p t J ] p_t\equiv \left[ p_t^1,\,\cdots,\,p_t^J \right] pt≡[pt1,⋯,ptJ]
③ 交易策略 Trading strategy: { θ t } t = 0 T \{ \theta_t \}_{t=0}^{T} {θt}t=0T , θ t = [ θ t 1 , ⋯ , θ t J ] \theta_t=\left[ \theta_t^1,\,\cdots,\,\theta_t^J \right] θt=[θt1,⋯,θtJ] 是时刻 t t t 的投资组合(注意这里 θ \theta θ 并不是投资比例,而是持有量)
④ 现金流 Cash flows:交易策略 θ \theta θ 产生的现金流为:(不考虑交易摩擦等)
d t θ = θ t − 1 ⋅ ( p t + δ t ) − θ t ⋅ p t d 0 θ = − θ 0 ⋅ p 0 \begin{align} d_t^{\theta}=&\,\theta_{t-1}\cdot (p_t+\delta_t)-\theta_t\cdot p_t \\ d_0^{\theta}=&\, -\theta_0\cdot p_0 \end{align} dtθ=d0θ=θt−1⋅(pt+δt)−θt⋅pt−θ0⋅p0
- d t θ d_t^{\theta} dtθ 右边可以看成两项:第一项是按照旧的投资组合,此时得到的红利 δ t \delta_t δt ,加上按照这一时刻 t t t 的价格 p t p_t pt 平仓的现金流;第二项是按照新的投资组合的初始投资;
- d 0 θ d_0^{\theta} d0θ 就是初始的投资;
⑤ 市场域 Market Span: D \bold{D} D 代表通过所有不同交易策略能够产生的现金流串,称为市场域。市场域构成了一个向量空间,受到参与交易的证券数量约束, J J J 越大则 D \bold{D} D 一定不会更小,因此 D \bold{D} D 不一定是个完备空间。
D ( p , δ ) = { { d t } t = 0 T : ∃ θ s . t . d t θ = d t , ∀ t } \bold{D}(p,\,\delta)=\left\{ \{d_t\}_{t=0}^{T}:\,\,\exist\,\theta\,\,s.t.\,\,d_t^{\theta}=d_t,\,\,\forall\, t \right\} D(p,δ)={{dt}t=0T:∃θs.t.dtθ=dt,∀t}
⑥ 未来市场域 Furure Market Span:理论上可能存在的、除去 0 时刻现金流的现金流串所构成的市场域:
M ( p , δ ) = { d − 0 : d = ( d 0 , d − 0 ) ∈ D ( p , δ ) } \bold{M}(p,\,\delta)=\left\{ d_{-0}:\,\,d=(d_0,\,d_{-0})\in \bold{D}(p,\,\delta) \right\} M(p,δ)={d−0:d=(d0,d−0)∈D(p,δ)}
套利 Arbitrage
无套利和正线性定价规则 No-arbitrage and Positive Linear Pricing Rule
以下分别介绍无套利的定义以及正线性定价规则,并且将证明二者是等价的。
Definition M3:称交易策略 θ \theta θ 是套利的,当 d t θ > 0 , ∀ t ≥ 0 d_t^{\theta}>0,\,\,\forall t\geq 0 dtθ>0,∀t≥0 ;
- 理想的市场不应当存在套利机会;
- 套利说明可以做到任何时刻(包括 0 时刻)都是正的现金流,即不需要任何付出就可以“空手套白狼”;
Condition S1:无套利时,存在至少一个正的状态价格过程(state price process) ψ ≡ { ψ t } t ≥ 1 \psi\equiv \{\psi_t\}_{t\geq 1} ψ≡{ψt}t≥1 ,使得对于所有的可交易证券,他们当前市场价都可以表示成:
p 0 j = ∑ t ≥ 1 ψ t ⋅ δ t j ≡ ψ ∘ δ j j = 1 , ⋯ , J \begin{align} p_0^{j}=&\,\sum\limits_{t\geq 1}\psi_t\cdot \delta_t^j \equiv \psi\circ \delta^j \\ j=&\, 1,\,\cdots,\,J \end{align} p0j=j=t≥1∑ψt⋅δtj≡ψ∘δj1,⋯,J
- 其中 ⋅ \cdot ⋅ 分别为随机变量定义的内积,例如 x ⋅ y = ∑ ω ∈ Ω x ( ω ) y ( ω ) x\cdot y=\sum\limits_{\omega\in\Omega}x(\omega)y(\omega) x⋅y=ω∈Ω∑x(ω)y(ω) ;
- ψ t ( ω ) \psi_t(\omega) ψt(ω) 可以看作 t t t 时刻 ω \omega ω 状态下的贴现因子;
Theorem 2:对于有限经济,无套利(M3)与线性定价规则(S1)的存在性是等价的。
证明: S 1 ⇒ M 3 S1\Rightarrow M3 S1⇒M3 是显然的(我也不知道为什么显然。。。),我们接下来证明 M 3 ⇒ S 1 M3\Rightarrow S1 M3⇒S1 :
M 3 M3 M3 代表不存在套利时, D ∩ R + m + 1 = 0 \bold{D}\cap \bold{R}^{m+1}_{+}=\bold{0} D∩R+m+1=0 (这里 0 \bold{0} 0 代表原点,因为没有全为正的现金流,所以跟第一象限只相交于原点),说明原点在 D \bold{D} D 的边界上。而 D \bold{D} D 显然是一个凸集(线性组合可以看成是投资组合的线性组合)。根据 Minkovsky 超平面分离定理,存在一个非零向量 q ∈ R m + 1 q\in \bold{R}^{m+1} q∈Rm+1 使得:
q ∘ c ≥ q ∘ d , ∀ c ∈ R + m + 1 , d ∈ D q\circ c \geq q\circ d,\quad \forall c\in \bold{R}^{m+1}_+,\,\,d\in\bold{D} q∘c≥q∘d,∀c∈R+m+1,d∈D
取等时,当且仅当 c = d = 0 c=d=\bold{0} c=d=0 ;
- 由于 c c c 在第一象限,我们取 c = 0 c=\bold{0} c=0 ,为了满足 0 ≥ q ∘ d 0\geq q\circ d 0≥q∘d 和 0 ≥ q ∘ − d 0\geq q\circ -d 0≥q∘−d ,我们可以推出 q ∘ d = 0 q\circ d=0 q∘d=0 ( − d -d −d 相当于将策略取反,所以现金流也相反,因此这个现金流串也是可以得到的,也在 D \bold{D} D 中);也就是说,对任意 d ∈ D d\in \bold{D} d∈D ,这个 q q q 都可以使得 q ∘ d = 0 q\circ d= 0 q∘d=0 ;
- 当 q ∘ c > 0 q\circ c > 0 q∘c>0 时,由于 c ≠ 0 c\not=0 c=0 ,而且 c c c 是在第一象限任意取的,因此 q q q 的每一维都大于 0,即 q ≫ 0 q\gg0 q≫0 ;
第一个关于 q q q 的条件,我们可以得到:
∑ t = 0 T ∑ ω ∈ Ω q t ( ω ) d t ( ω ) = 0 ∑ ω ∈ Ω q 0 ( ω ) d 0 ( ω ) + ∑ t = 1 T ∑ ω ∈ Ω q t ( ω ) d t ( ω ) = 0 \begin{align} \sum\limits_{t=0}^{T}\sum\limits_{\omega\in\Omega} q_t(\omega)d_t(\omega)&\,=0 \\ \sum\limits_{\omega\in\Omega} q_0(\omega)d_0(\omega)+\sum\limits_{t=1}^{T}\sum\limits_{\omega\in\Omega} q_t(\omega)d_t(\omega)&\,=0 \\ \end{align} t=0∑Tω∈Ω∑qt(ω)dt(ω)ω∈Ω∑q0(ω)d0(ω)+t=1∑Tω∈Ω∑qt(ω)dt(ω)=0=0
我们令 ψ t ( ω ) = q t ( ω ) q 0 > 0 \psi_t(\omega)=\frac{q_t(\omega)}{q_0}\gt 0 ψt(ω)=q0qt(ω)>0 ,因此对于任意 ( d 0 , d − 0 ) ∈ D (d_0,\,d_{-0})\in \bold{D} (d0,d−0)∈D ,有:
− d 0 = ψ ∘ d − 0 = ∑ t = 1 T ∑ ω ∈ Ω ψ t ( ω ) d t ( ω ) -d_0=\psi\circ d_{-0}=\sum\limits_{t=1}^{T}\sum\limits_{\omega\in\Omega}\psi_t(\omega)d_t(\omega) −d0=ψ∘d−0=t=1∑Tω∈Ω∑ψt(ω)dt(ω)
(我这边向量维数有点搞懵了。。。)
特别地,对于证券 j j j ,有:
p 0 j = ψ ∘ δ j , j = 1 , ⋯ , J p_{0}^{j}=\psi \circ \delta^j,\quad j=1,\,\cdots,\,J p0j=ψ∘δj,j=1,⋯,J
可以理解成:投资的第一步往往就是按照投资策略买入或卖出某组初始资产,所以 − d 0 -d_0 −d0 就可以看作是价格啦
来看个例题吧(
Exercise 1:考虑一个只有两期、三种状态 { 1 , 2 , 3 } \{1,\,2,\,3\} {1,2,3} 的经济体。市场上有两支可交易证券,带来的可能收益为:
d 1 = [ 110 , 110 , 110 ] d 2 = [ 50 , 100 , 150 ] \begin{align} d^{1}=&\,[110,\,110,\,110] \\ d^{2}=&\,[50,\,100,\,150] \end{align} d1=d2=[110,110,110][50,100,150]
初始价格为 p 1 = p 2 = 100 p^1=p^2=100 p1=p2=100 ,判断该市场上是否存在套利机会。
解:由于只有两期,可以理解为,第一期买进的话,第二期就要卖出,或者第一期卖出,第二期就要买进。例如,第一期买入一手 p 1 p^1 p1 ,第二期卖出,就可以得到 10 元收益。
第一支证券在未来的任意状态下价格都会上涨 10%,可以认为是无风险利率,比如存银行。
要判断是否存在套利机会,按照上面的定理,我们可以判断是否能找到一个严格为正的状态价格过程,使得当前的价格能由未来的现金流来表示。设状态价格过程为 [ ψ 1 , ψ 2 , ψ 3 ] T [\psi_1,\,\psi_2,\,\psi_3]^T [ψ1,ψ2,ψ3]T ,则:
{ 110 ψ 1 + 110 ψ 2 + 110 ψ 3 = 100 50 ψ 1 + 100 ψ 2 + 150 ψ 3 = 100 ⇒ [ ψ 1 ψ 2 ψ 3 ] = [ − 2 11 2 11 0 ] + ψ 3 [ 1 − 2 1 ] \left\{ \begin{array}{l} 110\psi_1+110\psi_2+110\psi_3=100 \\ 50\psi_1+100\psi_2+150\psi_3=100 \\ \end{array} \right. \Rightarrow \begin{bmatrix} \psi_1 \\ \psi_2 \\ \psi_3 \end{bmatrix} =\begin{bmatrix} -\frac{2}{11} \\ \frac{2}{11} \\ 0 \end{bmatrix}+\psi_3 \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix} {110ψ1+110ψ2+110ψ3=10050ψ1+100ψ2+150ψ3=100⇒ ψ1ψ2ψ3 = −1121120 +ψ3 1−21
当 ψ 3 ∈ ( 2 11 , 6 11 ) \psi_3\in(\frac{2}{11},\,\frac{6}{11}) ψ3∈(112,116) 时, ψ 1 \psi_1 ψ1 、 ψ 2 \psi_2 ψ2 和 ψ 3 \psi_3 ψ3 都大于 0,因此不存在套利机会。
可以看出,第二支证券当前定价为 100 还是合理的。那么,如果 p 2 = 150 p^2=150 p2=150 ,显然价格是扭曲的,我们可以算一下状态价格过程:
{ 110 ψ 1 + 110 ψ 2 + 110 ψ 3 = 100 50 ψ 1 + 100 ψ 2 + 150 ψ 3 = 150 ⇒ [ ψ 1 ψ 2 ψ 3 ] = [ − 13 11 10 11 0 ] + ψ 3 [ 1 − 2 1 ] \left\{ \begin{array}{l} 110\psi_1+110\psi_2+110\psi_3=100 \\ 50\psi_1+100\psi_2+150\psi_3=150 \\ \end{array} \right. \Rightarrow \begin{bmatrix} \psi_1 \\ \psi_2 \\ \psi_3 \end{bmatrix}= \begin{bmatrix} -\frac{13}{11} \\ \frac{10}{11} \\ 0 \end{bmatrix} + \psi_3 \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix} {110ψ1+110ψ2+110ψ3=10050ψ1+100ψ2+150ψ3=150⇒ ψ1ψ2ψ3 = −111311100 +ψ3 1−21
可以发现 ψ 1 \psi_1 ψ1 和 ψ 2 \psi_2 ψ2 无法同时大于 0,因此存在套利机会。我们可以看到 p 2 p^2 p2 很可能会跌,因此我们可以做空 2 2 2 ,并且向银行存钱: d 0 = − 15 11 × 100 + 150 > 0 d_0=-\frac{15}{11}\times 100+150 > 0 d0=−1115×100+150>0 ,则在 1 时刻,不论是那种状态下:
d 1 = { 15 11 × 110 − 50 = 100 > 0 15 11 × 110 − 100 = 50 > 0 15 11 × 110 − 100 = 0 d_1=\left\{ \begin{array}{l} \frac{15}{11}\times 110-50=100 >0 \\ \frac{15}{11}\times 110-100=50 >0 \\ \frac{15}{11}\times 110-100=0\\ \end{array} \right. d1=⎩ ⎨ ⎧1115×110−50=100>01115×110−100=50>01115×110−100=0
也就是说不论什么情况下都可以赚钱(
接下来介绍无套利的七个性质:
Implication 1: One-price Principle
一价性:产生两个相同未来现金流的投资组合,一定在当前市场中具有相同支出。因为状态价格过程是未知的,但是实际存在且唯一的。因此对于 d ∈ D d\in \bold{D} d∈D ,对于任意能够产生 d d d 的投资策略 ϕ \phi ϕ ,它们初始的现金流都是一致的,都是:
Ψ 0 ( d ) ≡ ψ ∘ d − 0 for all ∈ D \Psi_0(d)\equiv \psi\circ d_{-0}\quad \text{for all}\,\,\in\bold{D} Ψ0(d)≡ψ∘d−0for all∈D
一价性说明每个未来现金流都对应现在某个价格,这个映射可以表示为价格函数 Ψ 0 \Psi_0 Ψ0 ,价格函数是 well define 的。
Implication 2: Positivity
正性:对于任意非负未来现金流 d ∈ D d\in \bold{D} d∈D ,都有 Ψ 0 ( d ) ≥ 0 \Psi_0(d)\geq 0 Ψ0(d)≥0:
- 当 d − 0 = 0 d_{-0}=0 d−0=0 , Ψ 0 ( d ) = 0 \Psi_0(d)=0 Ψ0(d)=0 ,即什么都不做;
- 当 d − 0 > 0 d_{-0}>0 d−0>0 , Ψ 0 ( d ) > 0 \Psi_0(d)>0 Ψ0(d)>0 ,即要赚到钱,不可能什么都不做;
Implication 3: Additivity
可加性:对于任意 d ′ d' d′ , d ′ ′ ∈ D d''\in \bold{D} d′′∈D ,有 d ′ + d ′ ′ ∈ D d'+d''\in \bold{D} d′+d′′∈D ,特别地:
Ψ 0 ( d ′ + d ′ ′ ) = Ψ 0 ( d ′ ) + Ψ 0 ( d ′ ′ ) \Psi_0(d'+d'')=\Psi_0(d')+\Psi_0(d'') Ψ0(d′+d′′)=Ψ0(d′)+Ψ0(d′′)
这说明,两个投资组合的总投入,等同于要达到两个投资组合的未来现金流之和得到的新的未来现金流所需要的投入。
Implication 4: Homogeneity
齐次性:对于任意 d ∈ D d\in\bold{D} d∈D ,以及实数 α \alpha α ,有: Ψ 0 ( α d ) = α Ψ 0 ( d ) \Psi_0(\alpha d)=\alpha\Psi_0(d) Ψ0(αd)=αΨ0(d)
相当于把原来的持有量翻 α \alpha α 倍。
Implication 1-4 可以证明得到价格函数 Ψ 0 ( d ) \Psi_0(d) Ψ0(d) 是一个正比例函数。
Implication 5: Recursivity
递归性:对于任意 d ∈ D d\in \bold{D} d∈D ,0 时刻的价格 Ψ 0 ( d ) \Psi_0(d) Ψ0(d) 为:
Ψ 0 ( d ) = ∑ t ≥ 1 ψ t ⋅ d t \Psi_0(d)=\sum\limits_{t\geq 1}\psi_t \cdot d_t Ψ0(d)=t≥1∑ψt⋅dt
并且, Ψ 0 ( d ) \Psi_0(d) Ψ0(d) 还可以表示为未来第一期现金流加上未来第一期价格 Ψ 1 ( d ) \Psi_1(d) Ψ1(d) 的贴现值,即:
Ψ 0 ( d ) = ψ 1 ⋅ [ d 1 + Ψ 1 ( d ) ] \Psi_0(d)=\psi_1 \cdot [d_1+\Psi_1(d)] Ψ0(d)=ψ1⋅[d1+Ψ1(d)]
- 其中 ⋅ \cdot ⋅ 分别为随机变量定义的内积,例如 x ⋅ y = ∑ ω ∈ Ω x ( ω ) y ( ω ) x\cdot y=\sum\limits_{\omega\in\Omega}x(\omega)y(\omega) x⋅y=ω∈Ω∑x(ω)y(ω) ;
这相当于得到了一个倒向差分方程。
Implication 6: Risk-neutral Pricing Rule
风险中性定价规则:在事件空间 ( Ω , F ) (\Omega,\,\mathcal{F}) (Ω,F) 上定义概率测度 Q \bold{Q} Q ,使得对于事件 A A A ,有:
Q ( A ) ≡ ∑ ω ∈ A ψ 1 ( ω ) ∑ ω ∈ Ω ψ 1 ( ω ) \bold{Q}(A)\equiv \frac{\sum\limits_{\omega\in A}\psi_1(\omega)}{\sum\limits_{\omega\in\Omega}\psi_1(\omega)} Q(A)≡ω∈Ω∑ψ1(ω)ω∈A∑ψ1(ω)
测度 Q \bold{Q} Q 被称为风险中性概率测度。
考虑一个无风险的、收益率为 R 0 f = 1 + r 0 R_0^{f}=1+r_0 R0f=1+r0 的一期的贴现债券,由递归性可得:
1 1 + r 0 = ∑ ω ∈ Ω ψ 1 ( ω ) \frac{1}{1+r_0}=\sum\limits_{\omega\in\Omega}\psi_1(\omega) 1+r01=ω∈Ω∑ψ1(ω)
(因为无风险,所以所有状态下 d ( ω ) d(\omega) d(ω) 都相等;又因为只有一期,所以把 d 1 + Ψ 1 ( d ) d_1+\Psi_1(d) d1+Ψ1(d) 除到左边去,得到 1 1 + r 0 \frac{1}{1+r_0} 1+r01 ,右边就剩下了所有 ψ 1 ( ω ) \psi_1(\omega) ψ1(ω) 之和)
也就是 Implication 5 ⇒ \Rightarrow ⇒ Implication 6
对于任意 d ∈ D d\in \bold{D} d∈D ,我们有:
Ψ 0 ( d ) = 1 1 + r 0 E Q [ d 1 + Ψ 1 ( d ) ∣ F 0 ] = 1 R 0 f E Q [ d 1 + Ψ 1 ( d ) ∣ F 0 ] \Psi_0(d)=\frac{1}{1+r_0}\bold{E_Q}[d_1+\Psi_1(d)\,|\,\mathcal{F_0}]=\frac{1}{R_0^f}\bold{E_Q}[d_1+\Psi_1(d)\,|\,\mathcal{F_0}] Ψ0(d)=1+r01EQ[d1+Ψ1(d)∣F0]=R0f1EQ[d1+Ψ1(d)∣F0]
(可以看到 Q ( A ) \bold{Q}(A) Q(A) 的分母就是 1 1 + r 0 \frac{1}{1+r_0} 1+r01 )
也就是说,0 时刻的定价等于其近期未来股息支付加上其市值之和的贴现价值。
风险中性定价规则可以扩展到任意时间段:
Ψ t ( d ) = 1 R t f E Q [ d t + 1 + Ψ t + 1 ( d ) ∣ F t ] \Psi_t(d)=\frac{1}{R_t^f}\bold{E_Q}[d_{t+1}+\Psi_{t+1}(d)\,|\,\mathcal{F_t}] Ψt(d)=Rtf1EQ[dt+1+Ψt+1(d)∣Ft]
Implication 7: Risk-free Return Rule
无风险收益规则:对于任意 d ∈ D d\in\bold{D} d∈D ,记时刻 t t t 的总收益率为:
R t + 1 d = d t + 1 + Ψ t + 1 ( d ) Ψ t ( d ) R_{t+1}^{d}=\frac{d_{t+1}+\Psi_{t+1}(d)}{\Psi_t(d)} Rt+1d=Ψt(d)dt+1+Ψt+1(d)
在风险中心概率测度 Q \bold{Q} Q 下,对于任意现金流串 d ∈ D d\in\bold{D} d∈D ,其期望收益率都是一样的,为无风险利率,即:
E Q [ R t + 1 d ∣ F t ] = 1 + r t = R t f , ∀ t \bold{E_Q}[R_{t+1}^d\,|\,\mathcal{F}_t]=1+r_t=R_t^f,\quad \forall\,t EQ[Rt+1d∣Ft]=1+rt=Rtf,∀t
The Fundamental Theorem
Q \bold{Q} Q 和 P \bold{P} P 是不一样的, P \bold P P 代表的是未来某些状态出现的概率, Q \bold Q Q 则是正好满足概率的性质,所以定义了这样一个辅助量。并且在不完全的市场上,满足无套利性质的 Q \bold{Q} Q 是不唯一的。
Theorem:在有限经济中, M 3 M3 M3 , S 1 S1 S1 ,性质 5,性质 6 和性质 7 是相互等价的。并且和性质 1-4 的组合也是等价的。
-
M 3 ⟺ S 1 M3\iff S1 M3⟺S1 前面已经证明过了;
-
S 1 ⟺ ( 1 ) , ( 2 ) , ( 3 ) and ( 4 ) S1\iff (1),\,(2),\,(3)\,\text{and}\,(4) S1⟺(1),(2),(3)and(4) 可以通过正比例函数的性质得到;
-
S 1 ⇒ ( 5 ) ⇒ ( 6 ) ⇒ ( 7 ) S_1\Rightarrow (5) \Rightarrow (6) \Rightarrow(7) S1⇒(5)⇒(6)⇒(7) 都是在描述性质 5、6、7 时就证明了; ( 7 ) ⇒ M 3 (7)\Rightarrow M3 (7)⇒M3 在下面的练习中证明:
Exercise 2:在风险中性概率测度下,对于某个现金流串 d ∈ D d\in\bold{D} d∈D ,请证明其初始价格 Ψ 0 ( d ) \Psi_0(d) Ψ0(d) 可以表示为以下形式:
Ψ 0 ( d ) = E Q [ ∑ t = 1 T d t R 0 f ⋯ R t − 1 f + Ψ T ( d ) R 0 f ⋯ R T − 1 f ] , ∀ T ≥ 1 \Psi_0(d)=\bold{E_Q}\left[ \sum\limits_{t=1}^{T}\frac{d_t}{R_0^f\cdots R^f_{t-1}}+\frac{\Psi_T(d)}{R_0^f\cdots R^f_{T-1}} \right],\quad \forall \,T\geq 1 Ψ0(d)=EQ[t=1∑TR0f⋯Rt−1fdt+R0f⋯RT−1fΨT(d)],∀T≥1
证明:我只会倒推,就是把右边这个拆开,就可以得到初始时刻的价格。根据 Implication 6,我们有:
Ψ t ( d ) = 1 R t f E Q [ d t + 1 + Ψ t + 1 ( d ) ∣ F t ] = E Q [ d t + 1 R t f + Ψ t + 1 ( d ) R t f ] \Psi_t(d)=\frac{1}{R_t^f}\bold{E_Q}[d_{t+1}+\Psi_{t+1}(d)\,|\,\mathcal{F_t}]=\bold{E_Q}[\frac{d_{t+1}}{R_t^f}+\frac{\Psi_{t+1}(d)}{R_t^f}] Ψt(d)=Rtf1EQ[dt+1+Ψt+1(d)∣Ft]=EQ[Rtfdt+1+RtfΨt+1(d)]
则原式右边可以变为:
E Q [ ∑ t = 1 T d t R 0 f ⋯ R t − 1 f + Ψ T ( d ) R 0 f ⋯ R T − 1 f ] = E Q [ ∑ t = 1 T − 1 d t R 0 f ⋯ R t − 1 f ] + E Q [ d T R 0 f ⋯ R T − 1 f + Ψ T ( d ) R 0 f ⋯ R T − 1 f ] = E Q [ ∑ t = 1 T − 1 d t R 0 f ⋯ R t − 1 f ] + 1 R 0 f ⋯ R T − 2 f E Q [ d T R T − 1 f + Ψ T ( d ) R T − 1 f ] = E Q [ ∑ t = 1 T − 1 d t R 0 f ⋯ R t − 1 f ] + Ψ T − 1 ( d ) R 0 f ⋯ R T − 2 f = E Q [ ∑ t = 1 T − 2 d t R 0 f ⋯ R t − 1 f ] + E Q [ d T − 1 R 0 f ⋯ R T − 2 f + Ψ T − 1 ( d ) R 0 f ⋯ R T − 2 f ] = ⋯ = E Q [ d 1 R 0 f + Ψ 1 ( d ) R 0 f ] = Ψ 0 ( d ) \begin{align} &\,\bold{E_Q}\left[ \sum\limits_{t=1}^{T}\frac{d_t}{R_0^f\cdots R^f_{t-1}}+\frac{\Psi_T(d)}{R_0^f\cdots R^f_{T-1}} \right] \\ =&\, \bold{E_Q}\left[ \sum\limits_{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R^f_{t-1}}\right] + \bold{E_Q}\left[ \frac{d_T}{R_0^f\cdots R^f_{T-1}}+\frac{\Psi_T(d)}{R_0^f\cdots R^f_{T-1}} \right] \\ =&\, \bold{E_Q}\left[ \sum\limits_{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R^f_{t-1}}\right] + \frac{1}{R_0^f\cdots R_{T-2}^f}\bold{E_Q}\left[ \frac{d_T}{R^f_{T-1}}+\frac{\Psi_T(d)}{R^f_{T-1}} \right] \\ =&\, \bold{E_Q}\left[ \sum\limits_{t=1}^{T-1}\frac{d_t}{R_0^f\cdots R^f_{t-1}}\right] + \frac{\Psi_{T-1}(d)}{R_0^f\cdots R_{T-2}^f} \\ =&\, \bold{E_Q}\left[ \sum\limits_{t=1}^{T-2}\frac{d_t}{R_0^f\cdots R^f_{t-1}}\right] + \bold{E_Q}\left[ \frac{d_{T-1}}{R_0^f\cdots R^f_{T-2}}+\frac{\Psi_{T-1}(d)}{R_0^f\cdots R^f_{T-2}} \right] \\ =&\, \cdots \\ =&\, \bold{E_Q}\left[ \frac{d_{1}}{R_0^f}+\frac{\Psi_{1}(d)}{R_0^f} \right] \\ =&\, \Psi_0(d) \end{align} =======EQ[t=1∑TR0f⋯Rt−1fdt+R0f⋯RT−1fΨT(d)]EQ[t=1∑T−1R0f⋯Rt−1fdt]+EQ[R0f⋯RT−1fdT+R0f⋯RT−1fΨT(d)]EQ[t=1∑T−1R0f⋯Rt−1fdt]+R0f⋯RT−2f1EQ[RT−1fdT+RT−1fΨT(d)]EQ[t=1∑T−1R0f⋯Rt−1fdt]+R0f⋯RT−2fΨT−1(d)EQ[t=1∑T−2R0f⋯Rt−1fdt]+EQ[R0f⋯RT−2fdT−1+R0f⋯RT−2fΨT−1(d)]⋯EQ[R0fd1+R0fΨ1(d)]Ψ0(d)
二叉树期权定价模型
例:假设当前股票价格为 $100,并且你认为三个月后,股票价格将等可能地上涨 20% 至 $120 或下跌 10% 至 $90。假设 3 个月的无风险利率为 2%(虽然不可能这么高,但是为了方便计算)。考虑该股票的一个欧式看涨期权,期限为三个月,敲定价为 $100。则该期权当前的合理定价为多少?
解:一个简单的想法,考虑到期时期望收益的贴现值:
0.5 × ( 120 − 100 ) + 0.5 × 0 1.02 = 9.80 \frac{0.5\times(120-100)+0.5\times 0}{1.02}=9.80 1.020.5×(120−100)+0.5×0=9.80
但是这样是不合理的,可以举出套利的反例。假定当前期权价格为 $C_0=\text{$}9.80$ ,考虑如下的投资组合:
- 向银行借 $ 9,700 ;
- 买 113 股股票;
- 卖出 130 份期权。
则 0 时刻的现金流为:
d 0 = 170 × 9.8 + 9700 − 113 × 110 = $ 66 d_0=170\times9.8+9700-113\times110=\$ 66 d0=170×9.8+9700−113×110=$66
三个月后平仓并偿还银行的贷款,现金流为:
d 1 = { − 170 × 20 − 9700 × 1.02 + 113 × 120 = $ 266 if goes up − 170 × 0 − 9700 × 1.02 + 113 × 90 = $ 276 if goes down d_1=\left\{ \begin{array}{ll} -170\times 20-9700\times 1.02+113\times 120=\$266 & \text{if goes up} \\ -170\times 0-9700\times 1.02+113\times 90=\$276 & \text{if goes down} \end{array} \right. d1={−170×20−9700×1.02+113×120=$266−170×0−9700×1.02+113×90=$276if goes upif goes down
说明当价格为 $C_0=\text{$}9.80$ 时,存在套利机会。我们用两种方法得到正确的期权定价:
Approach One:Risk-Neutral Pricing :在风险中性概率测度下,令 q h > 0 q_h >0 qh>0 且 q l = 1 − q h > 0 q_l=1-q_h>0 ql=1−qh>0 ,分别对应价格上涨和下跌的“概率”。由概率测度的归一性和 Implication 7 可得:
{ q h + q l = 1 1.20 q h + 0.90 q l = 1.02 ⇒ { q h = 0.4 q l = 0.6 \left\{ \begin{array}{l} q_h+q_l=1 \\ 1.20q_h+0.90q_l=1.02 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} q_h=0.4 \\ q_l=0.6 \end{array} \right. {qh+ql=11.20qh+0.90ql=1.02⇒{qh=0.4ql=0.6
根据 Implication 6,当前期权价格为:
C 0 = 0.4 × ( 120 − 100 ) + 0.6 × 0 1.02 = $ 7.84 C_0=\frac{0.4\times(120-100)+0.6\times 0}{1.02}=\$7.84 C0=1.020.4×(120−100)+0.6×0=$7.84
Approach Two:Dulplicate Pricing :(这有点像凑数字)考虑下列投资组合:
- 向银行借 $\frac{60}{102}\times 100 $ $ ;
- 持有 2 3 \frac{2}{3} 32 单位股票;
该投资组合在三个月内的结果收益很容易计算,即上涨状态为20美元,下跌状态为0美元。该组合在到期日的收益与标的期权的收益相一致,即二者的未来现金流一致。根据 Implication 1 的一价原则,期权的初始价格必须由投资组合的初始成本给出,即:
C 0 = 2 3 × 100 − 60 102 × 100 = $ 7.84 C_0=\frac{2}{3}\times 100-\frac{60}{102}\times 100=\$7.84 C0=32×100−10260×100=$7.84
单期期权定价模型 A Signle-period Model
令无风险利率为 R f = 1 + r R^f=1+r Rf=1+r ,假设 h > R f > l h>R^f>l h>Rf>l ,并且令 q h ≡ Q ( { h } ) q_h\equiv \bold{Q}(\{h\}) qh≡Q({h}) 且 q l ≡ Q ( { l } ) = 1 − q h q_l\equiv \bold{Q}(\{l\})=1-q_h ql≡Q({l})=1−qh 。由无套利的无风险收益规则,我们得到一般形式:
{ q h + q l = 1 q h h + q l l = R f ⇒ q h = R f − l h − l and q l = h − R f h − l \left\{ \begin{array}{l} q_h+q_l=1 \\ q_h h+q_ll=R^f \end{array} \right. \Rightarrow q_h=\frac{R^f-l}{h-l} \text{ and } q_l=\frac{h-R^f}{h-l} {qh+ql=1qhh+qll=Rf⇒qh=h−lRf−l and ql=h−lh−Rf
未定权益为 X T X_T XT ;根据风险中性定价规则,初始市场价为:
Ψ 0 ( X t ) = 1 1 + r E Q [ X T ] = 1 1 + r ( q h X h + q l X l ) \Psi_0(X_t)=\frac{1}{1+r}\bold{E_Q}[X_T]=\frac{1}{1+r}(q_hX_h+q_lX_l) Ψ0(Xt)=1+r1EQ[XT]=1+r1(qhXh+qlXl)
特别地,对于敲定价为 X X X 的欧式看涨期权,初始价格为:
C 0 = 1 1 + r [ q h ( h S 0 − X ) + + q l ( l S 0 − X ) + ] C_0=\frac{1}{1+r}\left[q_h(hS_0-X)^++q_l(lS_0-X)^+\right] C0=1+r1[qh(hS0−X)++ql(lS0−X)+]
- 其中函数 ( x ) + = max { x , 0 } (x)^+=\max\{x,\,0\} (x)+=max{x,0}
- S 0 S_0 S0 是初始的股票价格
二叉树期权定价模型 CRR Binomial Model
前提假设:
- 无风险利率的固定期限结构: R f = 1 + r R^f=1+r Rf=1+r ;
- 二分的股票收益:股票收益 { R t } t ≥ 1 \{R_t\}_{t\geq 1} {Rt}t≥1 是相互独立的。每一时刻 R t R_t Rt 都可能上涨到原来的 h h h 或下跌到原来的 l l l ,并且假设 h > 1 + r > l h>1+r>l h>1+r>l ;
- 该股票在整个过程(到期日及到期日之前)中都没有分红
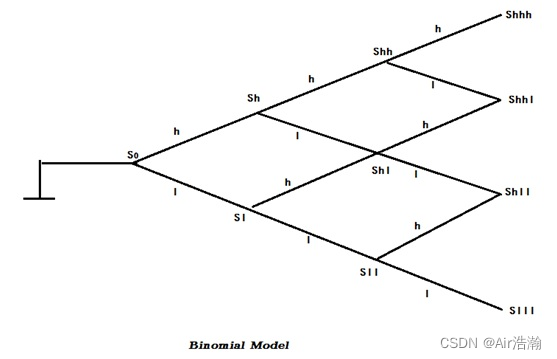
问题:确定未定收益 X ( S T ) X(S_T) X(ST) 的当前价格。
事件空间 Ω \Omega Ω 包括了在到期日之前所有二叉树上的路径:
- 例如对于 ω ∈ Ω \omega\in \Omega ω∈Ω ,常见形式为 ( h , ⋯ , l , ⋯ ) (h,\,\cdots,\,l,\,\cdots) (h,⋯,l,⋯) ;
- Ω \Omega Ω 中由 2 T 2^T 2T 条路径。对于任意时刻 t t t 和任意状态 ω ∈ Ω \omega\in\Omega ω∈Ω , F t ( ω ) \mathcal{F}_t(\omega) Ft(ω) 代表所有与 ω \omega ω 共享 t t t 时刻历史路径的所有未来路径。
- t = 0 t=0 t=0 , F 0 ( ω ) = Ω \mathcal{F}_0(\omega)=\Omega F0(ω)=Ω , ∀ ω \forall \omega ∀ω ;
- t ≥ 0 t\geq0 t≥0 , F 0 ( ω ) \mathcal{F}_0(\omega) F0(ω) , ∀ ω \forall \omega ∀ω 共有 2 T − t 2^{T-t} 2T−t 条不同的路径;
按照无风险收益规则(Implication 7),存在风险中性概率测度 Q \bold{Q} Q 使得:
E ! [ R t + 1 ∣ F t ( ω ) ] = 1 + r \bold{E_!}[R_{t+1}\,|\,\mathcal{F}_t(\omega)]=1+r E![Rt+1∣Ft(ω)]=1+r
在测度 Q \bold{Q} Q 下,下一时期股票收益为“高”值的概率为:
q h ( t , ω ) = Q ( R t + 1 = h ∣ F t ( ω ) ) = 1 − q l ( t , ω ) q_h(t,\,\omega)=\bold{Q}(R_{t+1}=h\,|\,\mathcal{F}_t(\omega))=1-q_l(t,\,\omega) qh(t,ω)=Q(Rt+1=h∣Ft(ω))=1−ql(t,ω)
无套利的条件要求对任意时刻:
q h ( t , ω ) = R f − l h − l = 1 − q l ( t , ω ) q_h(t,\,\omega)=\frac{R^f-l}{h-l}=1-q_l(t,\,\omega) qh(t,ω)=h−lRf−l=1−ql(t,ω)
在风险中性概率测度下,股票收益 { R t } t ≥ 1 \{R_t\}_{t\geq 1} {Rt}t≥1 构成了独立同分布的二项过程,我们由此可以得到对 X T X_T XT 的当前定价:
Proposition 1:到期日为 T T T 的未来未定收益 X ( S T ) X(S_T) X(ST) 的当前市场价为:
Ψ 0 ( X ) = 1 ( 1 + r ) T ∑ m = 0 T ( T m ) q h m q l T − m X ( h m l T − m S 0 ) \Psi_0(X)=\frac{1}{(1+r)^T}\sum\limits_{m=0}^{T}\binom{T}{m}q_h^mq_l^{T-m}X(h^ml^{T-m}S_0) Ψ0(X)=(1+r)T1m=0∑T(mT)qhmqlT−mX(hmlT−mS0)
- X ( h m l T − m S 0 ) X(h^ml^{T-m}S_0) X(hmlT−mS0) 应该是 ( h m l T − m S 0 − S 0 ) + (h^ml^{T-m}S_0-S_0)^+ (hmlT−mS0−S0)+
证明:由于没有分红,到期日之前 d t = 0 d_t=0 dt=0 ,因此根据风险中性定价规则(我觉得是根据 Exercise 2),有:
Ψ 0 ( X ) = 1 ( 1 + r ) T E Q [ X ( S T ) ] \Psi_0(X)=\frac{1}{(1+r)^T}\bold{E_Q}[X(S_T)] Ψ0(X)=(1+r)T1EQ[X(ST)]
显然,对于任意状态 ω ∈ Ω \omega\in\Omega ω∈Ω ,其股票价格取决于路径上 h 和 l 的数量,所以就是上面那样的式子。
倒向过程 Backward Procedure
这个二叉树也可以倒过来看:
- 在时刻 T T T , Ψ T ( m ) = X ( h m l T − m S 0 ) \Psi_T(m)=X(h^ml^{T-m}S_0) ΨT(m)=X(hmlT−mS0) , ∀ 0 ≤ m ≤ T \forall 0\leq m\leq T ∀0≤m≤T ;
- 在时刻 t ≤ T t\le T t≤T ,对于 ∀ 0 ≤ m ≤ T \forall 0\leq m\leq T ∀0≤m≤T ,价格为:
Ψ t ( m ) = 1 1 + r × [ q h Ψ t + 1 ( m + 1 ) + q l Ψ t + 1 ( m ) ] \Psi_t(m)=\frac{1}{1+r}\times[q_h\Psi_{t+1}(m+1)+q_l\Psi_{t+1}(m)] Ψt(m)=1+r1×[qhΨt+1(m+1)+qlΨt+1(m)]
- 在初始时刻 0 0 0 ,价格为 Ψ 0 ( 0 ) \Psi_0(0) Ψ0(0) ;
带有常数红利的期权定价 Option Pricing with Constant Dividend Yield
对于带有常数红利率 κ \kappa κ 的股票,即 δ t = κ S t − 1 , t ≥ 1 \delta_t=\kappa S_{t-1},\,\, t\geq 1 δt=κSt−1,t≥1 ,则风险中性概率变为:
q h = R f − κ − l h − l = 1 − q l q_h=\frac{R^f-\kappa-l}{h-l}=1-q_l qh=h−lRf−κ−l=1−ql
此时我们的假设要变为 h + κ > R f > l + κ h+\kappa > R^f > l+\kappa h+κ>Rf>l+κ
例:对于某个欧式看涨期权给出以下具体数据:
- 常数红利率为 κ = 2 % \kappa=2\% κ=2% ;
- 股票价格上涨或下跌的幅度为 5 % 5\% 5% ;
- 无风险利率为每期 2 % 2\% 2% ;
- 初始时刻的股票价格为 $$100$ ;
- 到期期限为 T = 5 T=5 T=5 ,敲定价格为 $$100$ ;
股票价格过程为:
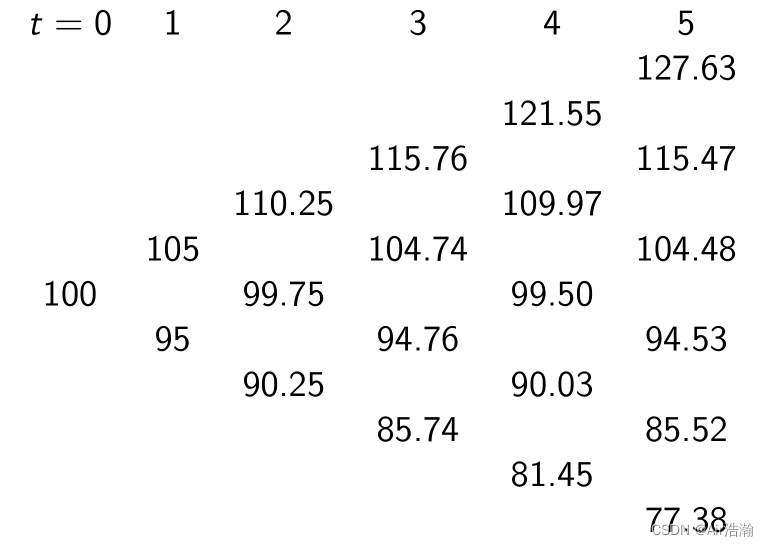
风险中性概率为:
q h = R f − l − k h − l = 0.5 q_h=\frac{R^f-l-k}{h-l}=0.5 qh=h−lRf−l−k=0.5
倒向价格过程为:
C t , m = C t + 1 , m + C t + 1 , m + 1 2 × 1.02 C_{t,\,m}=\frac{C_{t+1,\,m}+C_{t+1,\,m+1}}{2\times1.02} Ct,m=2×1.02Ct+1,m+Ct+1,m+1
期权价格过程为:

美式期权定价问题
美式期权在到期日及之前都可以行权,这里我们也是用二叉树期权定价模型,考虑离散的情况。
对于标的股票为 S S S 的美式看涨期权,其敲定价为 X X X ,在 ( t , ω ) (t,\,\omega) (t,ω) 情况下的收益为:
- t < T t< T t<T : X t ( ω ) = S t ( ω ) − X X_t(\omega)=S_t(\omega)-X Xt(ω)=St(ω)−X ;
- t = T t=T t=T : X T ( ω ) = ( S T ( ω ) − X ) + X_T(\omega)=(S_T(\omega)-X)^+ XT(ω)=(ST(ω)−X)+ ;
(看跌期权就是相应地变为 X − S t ( ω ) X-S_t(\omega) X−St(ω) 和 ( S T ( ω ) − X ) + (S_T(\omega)-X)^+ (ST(ω)−X)+)
直观理解一下,由于美式期权更为灵活,因此定价往往更高。离散时间的美式期权定价涉及到两个问题:
- 在时刻 t < T t< T t<T 以及当时的信息 F t ( ω ) \mathcal{F}_t(\omega) Ft(ω) ,如何对该期权进行合理定价?
- 期权持有者选择在什么时间和什么状态行使他们的期权?
Theorem 5:美式期权的定价 { Ψ t ( X ) } t = 0 T \{\Psi_t(X)\}_{t=0}^{T} {Ψt(X)}t=0T 和最佳行权时间 τ ∗ \tau^* τ∗ 满足:
- 对于 ∀ ( t , ω ) \forall (t,\,\omega) ∀(t,ω) ,有:
Ψ t ( X ; ω ) = max { X t ( ω ) , 1 1 + r E Q [ Ψ t + 1 ( X ) ∣ F t ( ω ) ] } \Psi_t(X;\,\omega)=\max\left\{ X_t(\omega),\,\frac{1}{1+r}\bold{E_Q}\left[\Psi_{t+1}(X)\,|\,\mathcal{F}_t(\omega) \right] \right\} Ψt(X;ω)=max{Xt(ω),1+r1EQ[Ψt+1(X)∣Ft(ω)]}
- 对于 ∀ ( t , ω ) \forall (t,\,\omega) ∀(t,ω) , τ ∗ = t \tau^*=t τ∗=t 当且仅当: Ψ s ( X ; ω ) > X s ( ω ) \Psi_s(X;\,\omega)>X_s(\omega) Ψs(X;ω)>Xs(ω) ∀ s < t \forall s<t ∀s<t 并且 Ψ t ( X ; ω ) = X t ( ω ) \Psi_t(X;\omega)=X_t(\omega) Ψt(X;ω)=Xt(ω) ,或者表述为:
τ ∗ ( ω ) = inf { t ∈ { 0 , ⋯ , T } : Ψ t ( X ; ω ) = X t ( ω ) } , ∀ ω ∈ Ω \tau^*(\omega)=\inf\left\{ t\in\{0,\,\cdots,\,T\}:\,\Psi_t(X;\,\omega)=X_t(\omega) \right\},\,\forall\omega\in\Omega τ∗(ω)=inf{t∈{0,⋯,T}:Ψt(X;ω)=Xt(ω)},∀ω∈Ω
Proposition 6:考虑一个标的股票无分红的美式看涨期权,投资者在到期日之前都不会行权,即 τ ∗ ≡ T \tau^*\equiv T τ∗≡T ,也就是说此时美式看涨期权和欧式看涨期权的定价相同。
证明:按照定义,美式看涨期权在 ( t , ω ) (t,\,\omega) (t,ω) 情况下行权的的收益为 S t ( ω ) − X S_t(\omega)-X St(ω)−X ;并且按照 Th5 的性质 1,美式看涨期权的价值不低于同时刻的欧式看涨期权,即:
Ψ t ( X ; ω ) ≥ 1 ( 1 + r ) T − t E Q [ ( S T ( ω ) − X ) + ∣ F t ( ω ) ] ≥ 1 ( 1 + r ) T − t E Q [ S T ( ω ) − X ∣ F t ( ω ) ] = S t ( ω ) − 1 ( 1 + r ) T − t X ≥ S t ( ω ) − X \begin{align} \Psi_t(X;\,\omega) \geq&\, \frac{1}{(1+r)^{T-t}}\bold{E_Q}[(S_T(\omega)-X)^+\,|\,\mathcal{F}_t(\omega)] \\ \geq&\, \frac{1}{(1+r)^{T-t}}\bold{E_Q}[S_T(\omega)-X\,|\,\mathcal{F}_t(\omega)] \\ =&\, S_t(\omega)-\frac{1}{(1+r)^{T-t}}X \\ \geq &\, S_t(\omega)-X \end{align} Ψt(X;ω)≥≥=≥(1+r)T−t1EQ[(ST(ω)−X)+∣Ft(ω)](1+r)T−t1EQ[ST(ω)−X∣Ft(ω)]St(ω)−(1+r)T−t1XSt(ω)−X
-
第一个不等号是由 Theorem 5 给出,美式看涨期权的价值不低于同时刻的欧式看涨期权;
-
第二个不等号是因为 ( x ) + = max { x , 0 } (x)^+=\max\{x,\,0\} (x)+=max{x,0} ,所以 ( x ) + ≥ x (x)^+\geq x (x)+≥x ;
-
第三个等号是因为期望的线性性, 1 ( 1 + r ) T − t E Q [ S t ( ω ) ] \frac{1}{(1+r)^{T-t}}\bold{E_Q}[S_t(\omega)] (1+r)T−t1EQ[St(ω)] 根据 Implicatio 6 就是此时的价格;
-
第四个不等号是因为通常来说 r > 0 r > 0 r>0 ;
最后一个不等号意味着除非 t = T t=T t=T ,否则 Ψ t ( X ; ω ) > S t ( ω ) − X \Psi_t(X;\,\omega)>S_t(\omega)-X Ψt(X;ω)>St(ω)−X ,那么投资者只会在 t = T t=T t=T 时有可能行权(行权至少也要 S T ( ω ) > X S_T(\omega)>X ST(ω)>X 吧hhh )。
又根据 Implication 1 的一价定律,此时美式看涨期权和欧式看涨期权在初始时刻的定价相同。
当然,对于带分红的标的股票,Proposition 6 是不成立的。由于美式看涨期权的定价带有 max \max max 运算,因此没法像欧式看涨期权一样写出正向解析式;对于某个具体的例子,我们可以通过倒向方程来推导。
例:对于某个美式看涨期权给出以下具体数据:
- 常数红利率为 κ = 2 % \kappa=2\% κ=2% ;
- 股票价格上涨或下跌的幅度为 5 % 5\% 5% ;
- 无风险利率为每期 2 % 2\% 2% ;
- 初始时刻的股票价格为 $$100$ ;
- 到期期限为 T = 5 T=5 T=5 ,敲定价格为 $$100$ ;
股票价格过程为(和前边欧式看涨期权一样):

风险中性概率为:
q h = R f − l − k h − l = 0.5 q_h=\frac{R^f-l-k}{h-l}=0.5 qh=h−lRf−l−k=0.5
倒向过程方程为:
A t , m = max { S t , m − K , A t + 1 , m + A t + 1 , m + 1 2 × 1.02 } A_{t,\,m}=\max\left\{ S_{t,\,m}-K,\,\frac{A_{t+1,\,m}+A_{t+1,\,m+1}}{2\times 1.02} \right\} At,m=max{St,m−K,2×1.02At+1,m+At+1,m+1}
期权价格过程为:
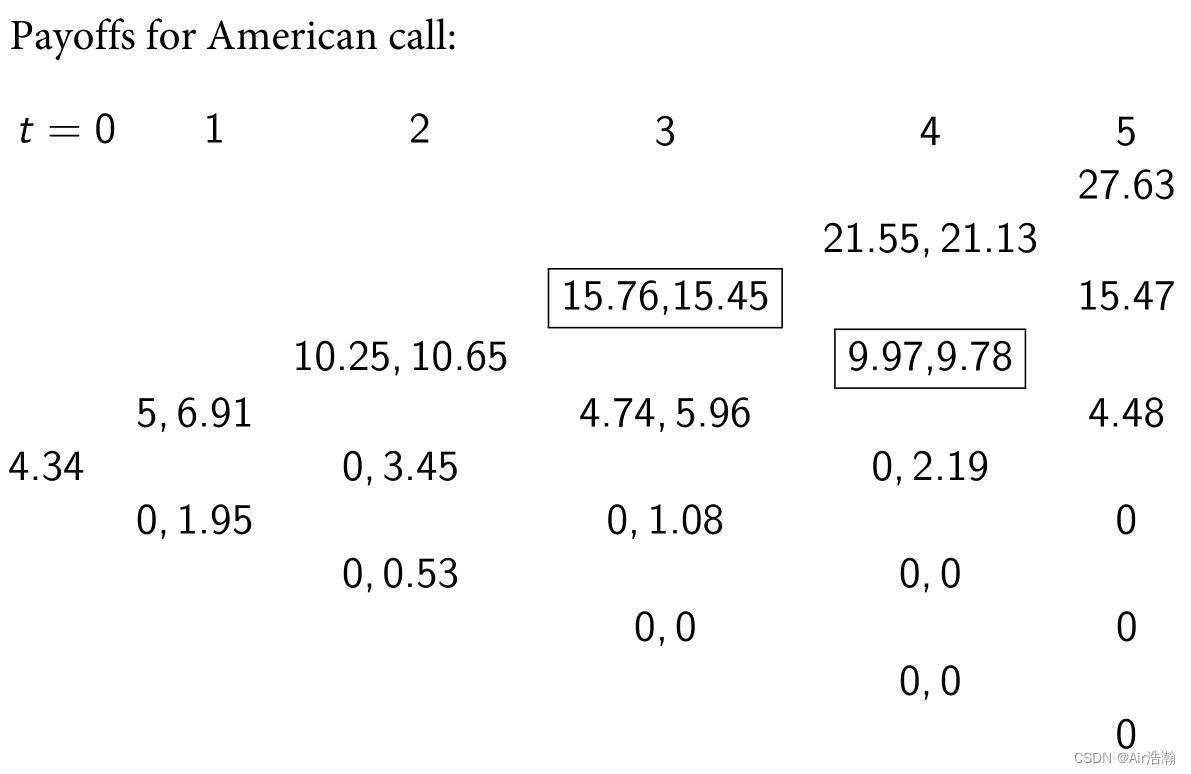
最佳行权时间为:
- 路径 { h , h , h } \{h,\,h,\,h\} {h,h,h} , τ ∗ = 3 \tau^*=3 τ∗=3 ;
- 当不是三个连续的 h h h ,但是有 3 个 h h h ( { l , h , h , h } \{l,\,h,\,h,\,h\} {l,h,h,h} , { h , l , h , h } \{h,\,l,\,h,\,h\} {h,l,h,h} 或 { h , h , l , h } \{h,\,h,\,l,\,h\} {h,h,l,h}), τ ∗ = 4 \tau^*=4 τ∗=4 ;
- 其他情况下, τ ∗ = 5 \tau^*=5 τ∗=5 ;
可以看到,和我们的直觉一致,在到期日之前,同时刻同状态下美式看涨期权的价格比欧式看涨期权要更高,但是在到期日是一样的。
相关文章:

量化投资 无套利 No-arbitrage
文章目录 量化投资 无套利 No-arbitrageState of Nature市场域 Market Span 套利 Arbitrage无套利和正线性定价规则 No-arbitrage and Positive Linear Pricing RuleImplication 1: One-price PrincipleImplication 2: PositivityImplication 3: AdditivityImplication 4: Homo…...

小程序容器助力智能移动门户统一
智能移动统一门户遵循“统一规划,统一标准,统一建设,统一运维”的指导思想。它灵活运用前端展示平台,微服务后端平台,流程引擎,规则引擎,非结构化数据平台,即时通讯平台,…...

opencv-python相机标定详解
文章目录 角点检测查看角点标定 opencv中内置了张正友的棋盘格标定法,通过一些姿态各异的棋盘格图像,就能标定相机的内外参数。 角点检测 第一步是角点检测,首先需要读取棋盘格图像 import numpy as np import cv2 import ospath imgs #…...

由斯坦福、Nautilus Chain等联合主办的 Hackathon 活动,现已接受报名
由 Stanford Blockchain Accelerator、Zebec Protocol、 Nautilus Chain、Rootz Lab 共同主办的黑客松活动,现已接受优秀项目提交参赛申请。 在加密行业发展早期,密码极客们就始终在对区块链世界基础设施,在发展方向的无限可能性进行探索。而…...
)
PBDB Data Service:Measurements of specimens(标本测量)
Measurements of specimens(标本测量) 描述参数以下参数可用于指定您感兴趣的标本种类以下参数可用于筛选所选内容以下参数还可用于根据分类筛选结果列表以下参数可用于生成数据存档您可以使用以下参数选择要检索的额外信息,以及要获取记录的…...
低调的接口工具 ApiKit
最近发现一款接口测试工具--ApiKit,我们很难将它描述为一款接口管理工具 或 接口自测试工具。 官方给了一个简单的说明,更能说明 Apikit 可以做什么。 ApiKit API 管理 Mock 自动化测试 异常监控 团队协作 ApiKit的特点: 接口文档定义&a…...
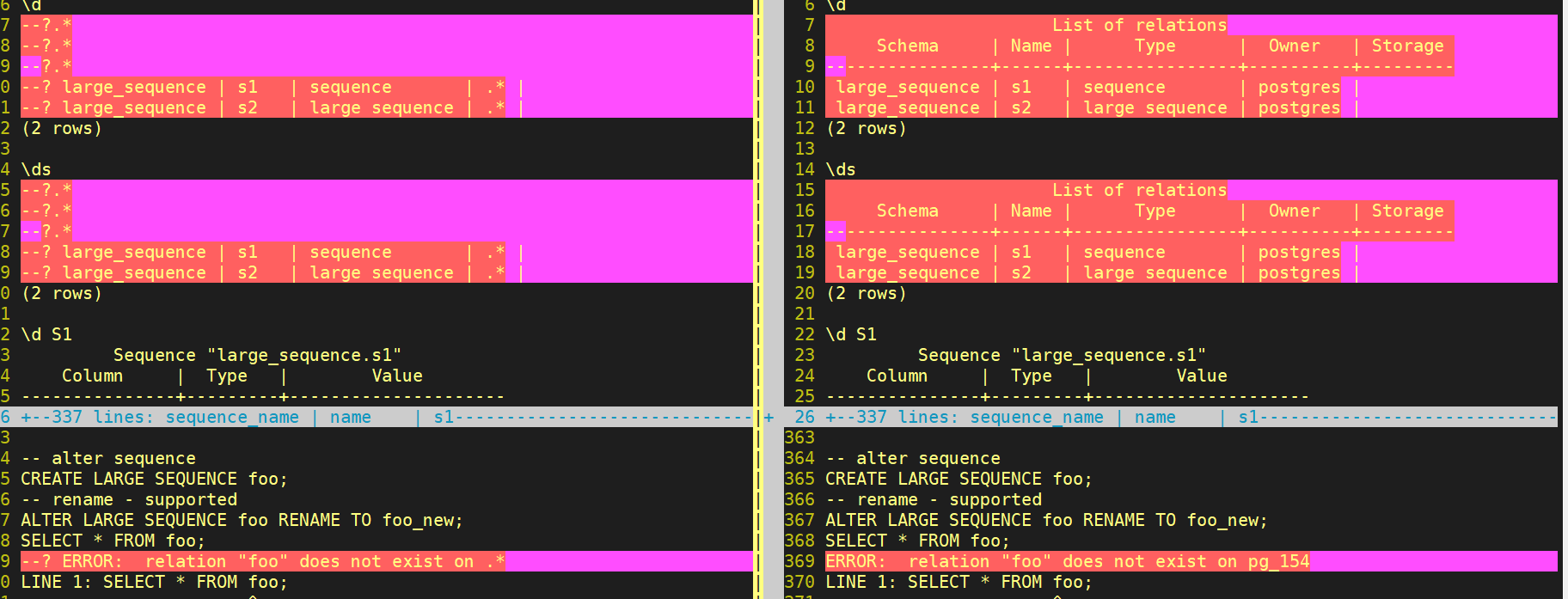
opengauss 的回归测试
目录 一、回归测试说明 二、单独执行测试用例(开发调试) 一、回归测试说明 opengauss/postgresql 的回归测试,通过执行SQL比较输出打印,判断代码修改是否改变了其它功能逻辑。 OG的回归测试大体上和PG类似,主要是通…...

计算机组成原理基础练习题第四章-计算机的运算方法
对真值0表示形式唯一的机器数是()。A、原码 B、补码和移码C、反码 D、以上都不对在整数定点机中,下述说法正确的是()。A、原码和反码不能表示-1,补码可以表示-1B、三种机器数均可表示-1C、三种机器数均可表示…...

SpringBoot定时任务里的多线程
SpringBoot定时任务里的多线程 提示前言遇到的问题验证与解决验证单线程执行单任务分析代码及结果 单线程执行多任务 解决实现单任务的多线程为每个任务创建一个子线程 解决多任务的多线程设定固定容量线程池动态设定容量线程池固定线程池和动态线程池的选择 简单总结借鉴及引用…...

YOLO V3 SPP ultralytics 第二节:根据yolo的数据集,生成准备文件和yolo的配置文件
目录 1. 介绍 2. 完整代码 3. 代码讲解 3.1 生成 my_train_data.txt和my_val_data.txt 3.2 生成 my_data.data 文件 3.3 生成 my_yolov3.cfg 3.4 关于my_data_label.names文件 1. 介绍 根据 第一节 的操作,已经生成了下图中圆圈中的部分,而本…...

camunda流程引擎connector如何使用
在 Camunda 中,Connector 是一种用于与外部系统或服务交互的机制。它允许 BPMN 模型中的 Service Task 节点与外部系统或服务进行通信,从而使流程更加灵活和可扩展。使用 Connector,可以将业务流程与外部系统集成在一起,而无需编写…...

ECO基本概念:pre-mask eco gen patch flow
使用conformal LEC 进行pre-mask eco 时,如何产生patch,参考以下步骤: 官方推荐 Flattened ECO Flow(FEF) Conformal支持Flattened ECO Flow和Hierarchical ECO Flow。Flattened下,工具会将 ECO 分析重点…...
【初学人工智能原理】【4】梯度下降和反向传播:能改(下)
前言 本文教程均来自b站【小白也能听懂的人工智能原理】,感兴趣的可自行到b站观看。 本文【原文】章节来自课程的对白,由于缺少图片可能无法理解,故放到了最后,建议直接看代码(代码放到了前面)。 代码实…...

微信小程序路由传参
微信小程序路由传参 在微信小程序中,可以通过路由传参将数据传递给目标页面。以下是一种常见的方式: 在源页面中,使用 wx.navigateTo 或 wx.redirectTo 方法跳转到目标页面,并通过 URL 参数传递数据。示例: wx.navi…...
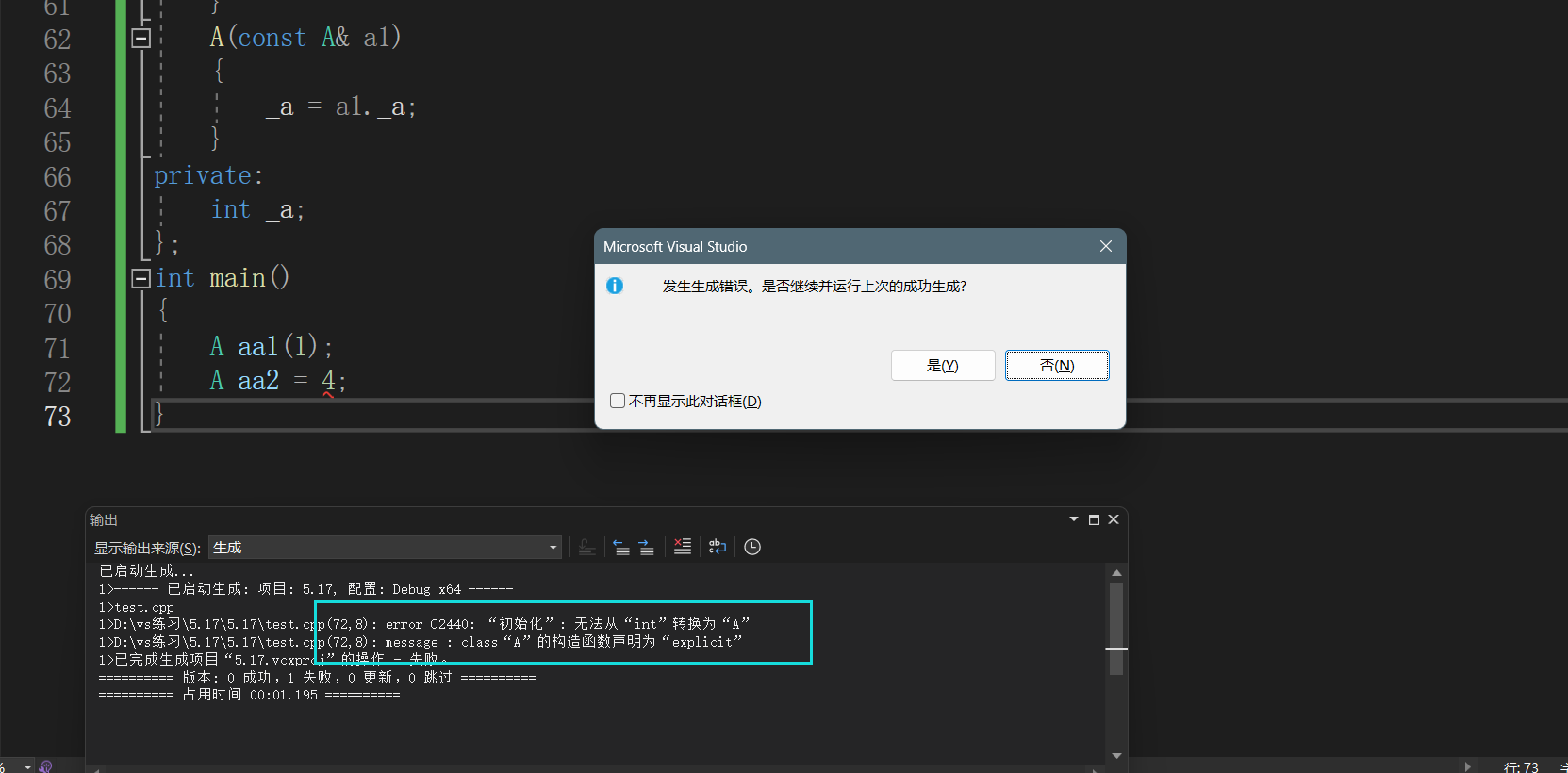
深入篇【C++】类与对象:再谈构造函数之初始化列表与explicit关键字
深入篇【C】类与对象:再谈构造函数之初始化列表与explicit关键字 Ⅰ.再谈构造函数①.构造函数体赋值②.初始化列表赋值【<特性分析>】1.至多性2.特殊成员必在性3.必走性:定义位置4.一致性5.不足性 Ⅱ.explicit关键字①.隐式类型转化②.作用 Ⅰ.再谈…...

广东棒球发展建设·棒球1号位
一、概述 棒球是一项源于美国的运动,自20世纪初开始传入中国,近年来在广东省的发展也逐渐受到关注。本文将就广东棒球的发展现状及未来发展方向进行分析。 二、发展现状 目前广东省内棒球赛事主要有以下几种: 1. 业余棒球联赛:…...

浅谈PMO对组织战略的支持︱美团骑行事业部项目管理中心负责人边国华
美团骑行事业部项目管理中心负责人边国华先生受邀为由PMO评论主办的2023第十二届中国PMO大会演讲嘉宾,演讲议题:浅谈PMO对组织战略的支持。大会将于6月17-18日在北京举办,更多内容请浏览会议日程 议题内容简要: 战略是组织运行的…...

互联网医院资质代办|互联网医院牌照的申请流程
随着互联网技术的不断发展,互联网医疗已经逐渐成为人们关注的热点话题。而互联网医院作为互联网医疗的一种重要形式,也越来越受到社会各界的关注。若想开展互联网医院业务,则需要具备互联网医院牌照。那么互联网医院牌照的申请流程和需要的资…...

网络:DPDK复习相关知识点_2
1.RTC运行至完成时模式,单核单模块 2.pipeline模式,多核多模块,每个模块都是一个处理引擎,但会有缓存一致性问题 3.Mbuff数据包内存操作对象,相当于是数据包的一个索引,对网络的处理都集中在这个Buff上 …...

阿里云大学考试Java中级题目及解析-java中级
阿里云大学考试Java中级题目及解析 1.servlet释放资源的方法是? A.int()方法 B.service()方法 C.close() 方法 D.destroy()方法 D servlet释放资源的方法是destroy() 2.order by与 group by的区别? A.order by用于排序,group by用于排序…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
