C++进阶——红黑树
C++进阶——红黑树
概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过
对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩
倍,因而是接近平衡的。
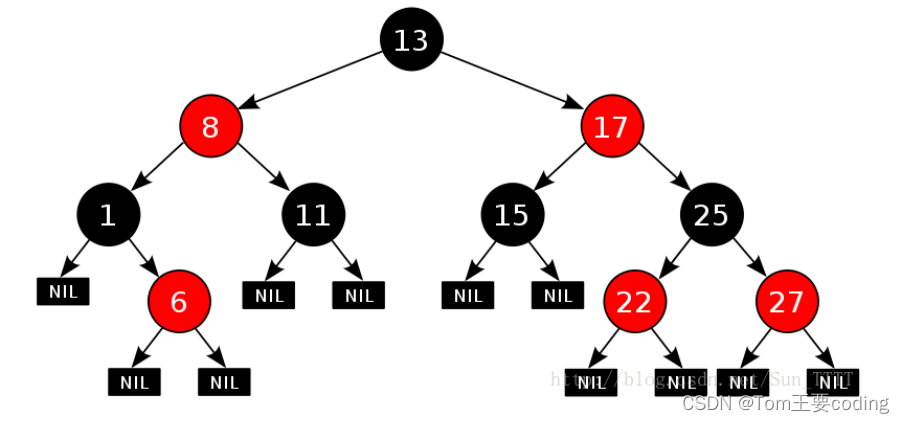
红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的(俩个红不能相邻)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
其实可以总结一下:最短的树枝一定是全黑的,最长的一定是红黑交替的,按照每个树枝黑节点都相同则全黑的一定是红黑相间的二倍。
实现红黑树
定义一个节点
enum color//定义颜色
{RED,BLACK
};
template<class K,class T>struct RBTreeNode{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;color _col;RBTreeNode(const pair(K, V)& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}};
思考:在节点的定义中,为什么要将节点的默认颜色给成红色的?
因为刚刚说的性质中第三条比第四条更好维护。
红黑树结构
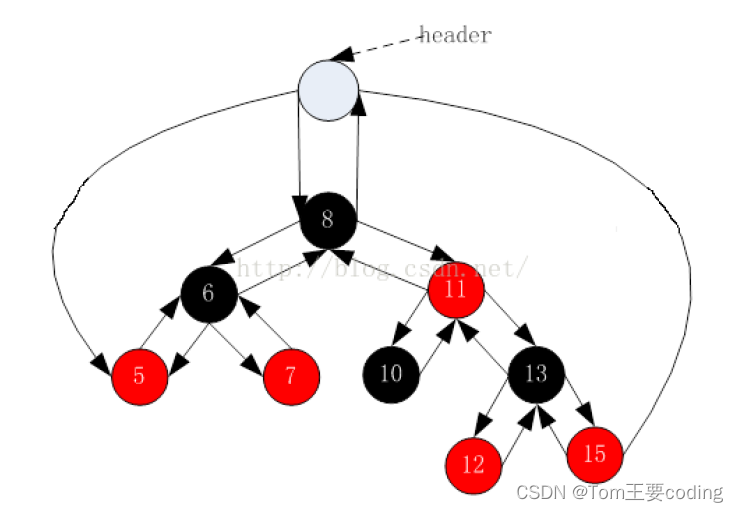
为了后续实现关联式容器简单,红黑树的实现中增加一个头结点,因为跟节点必须为黑色,为了与根节点进
行区分,将头结点给成黑色,并且让头结点的 pParent 域指向红黑树的根节点,pLeft域指向红黑树中最小的
节点,_pRight域指向红黑树中最大的节点,如下:
查找
其实结合普通二叉树一样就不多展开讲解了。
node* Find(const K& key){node* cur = _root;while (cur){if (cur->_kv > key){cur = cur->_left;}else if (cur->_kv < key){cur = cur->_right;}else{return cur;}}return nullptr;}
插入
前期插入也很简单,但是变色还有要控制变色之后整棵树的性质不变要做出——旋转。
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点。a、b、c、d、e都是高度不一定的子树(只要满足性质可以为空)。
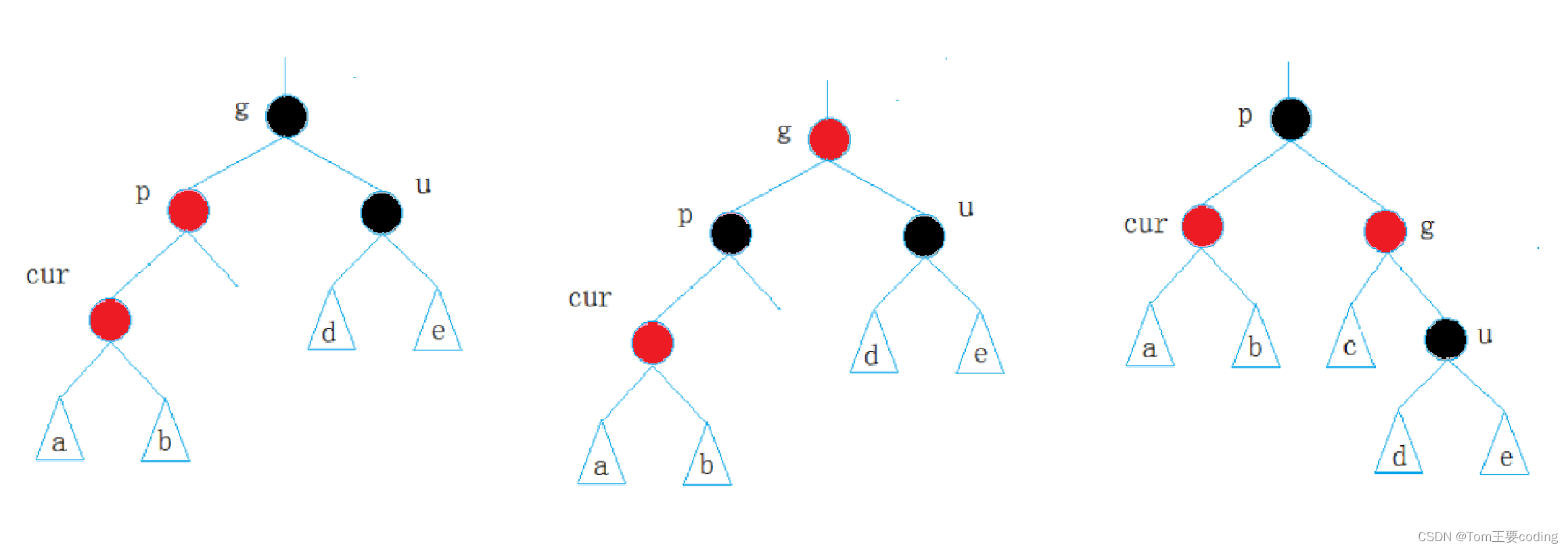
情况一: cur为红,p为红,g为黑,u存在且为红
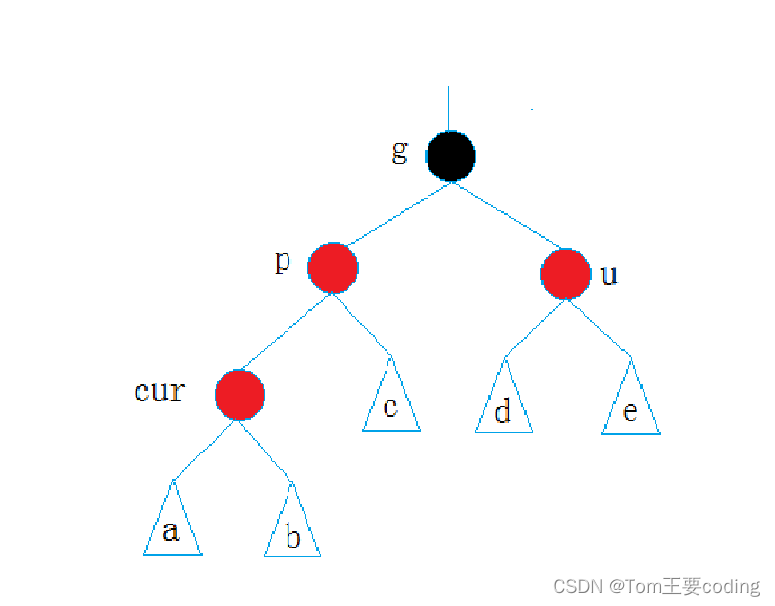
变色后:
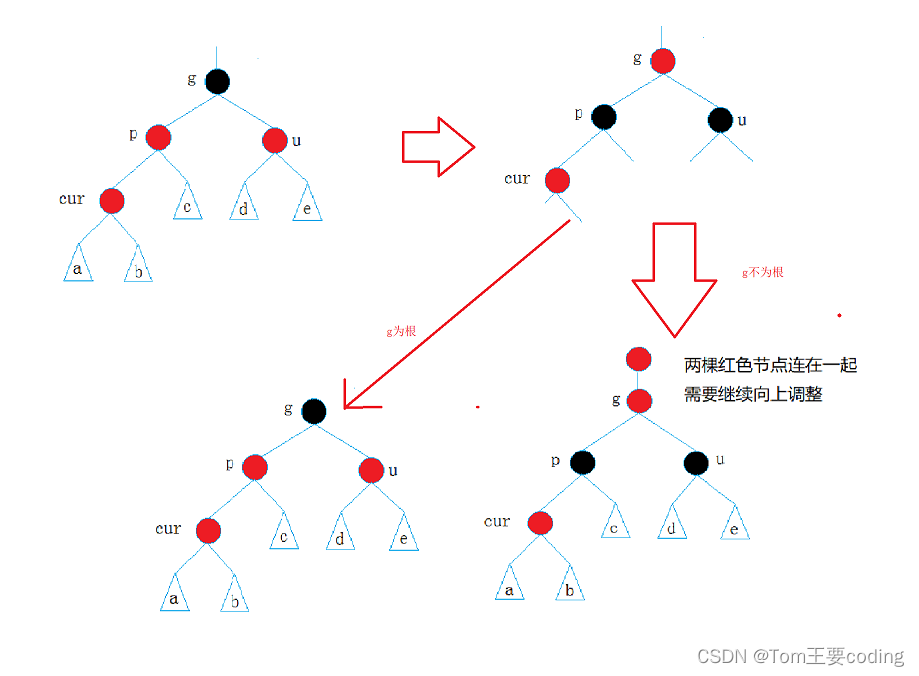
然后grandfather变成心得cur继续向上变色,直到g是根节点变成黑色,如果不是根节点就还是变成红色,并继续向上调整。
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
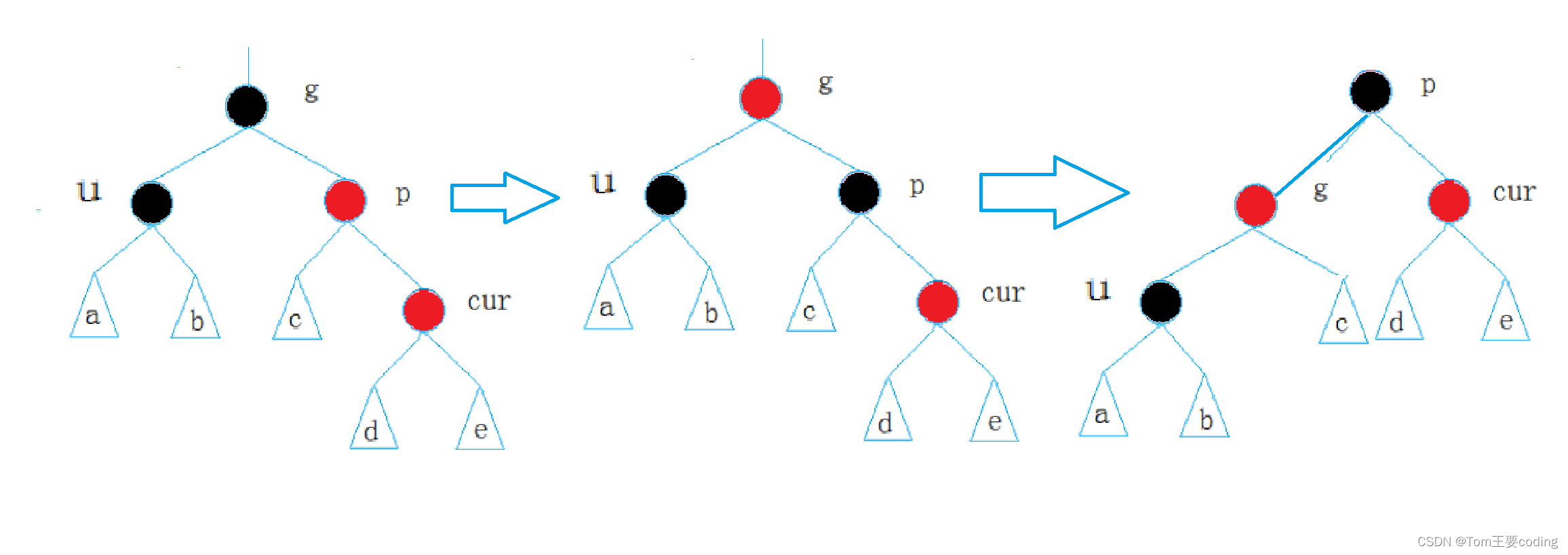
情况二: cur为红,p为红,g为黑,u不存在/u为黑
是一条线方向
右旋:
左旋:

p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红
情况三: cur为红,p为红,g为黑,u不存在/u为黑
但是是折线方向
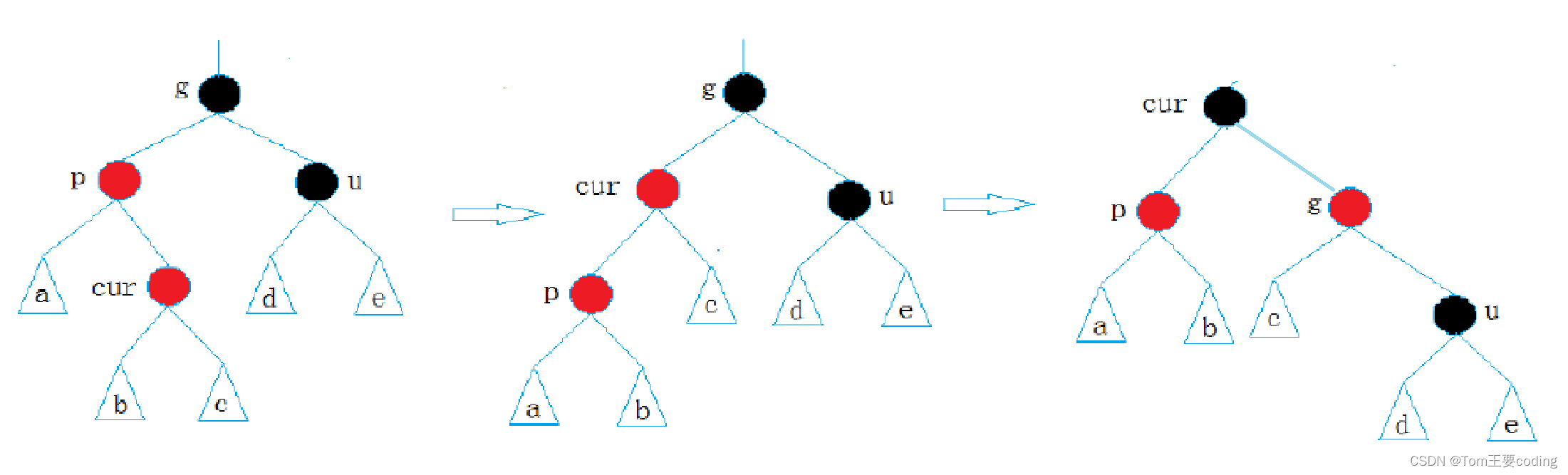
bool Insert(const pair<K,V>& kv){//先进行连接if (_root == nullptr){_root = new node(kv);_root->_col = BLACK;return true;}node* parent = nullptr;node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//接下来要开始变色了。while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (grandfather->_left == parent){node* uncle = grandfather->_right;//情况1:u存在且为红,变色处理,并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else//情况2+3:u不存在/u尊在且为黑——旋转加变色{// g// p u// c if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;}break;}}else//g->right=p{node* uncle = grandfather->_left;// 情况1:u存在且为红,变色处理,并继续往上处理if (uncle&& uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else//情况2+3:u不存在/u存在且为黑,旋转+变色{// g// u p// cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->col=BLACK;//根永远是黑色的。return true;}
检测
bool isBalance(){if (_root && _root->_col == RED){cout << "根节点颜色是红色" << endl;return false;}int benchmark = 0;node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 连续红色节点return _Check(_root, 0, benchmark);}
bool _Check(node* root, int blackNum, int benchmark){if (root == nullptr){if (benchmark != blackNum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}int _Height(node* root){if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void _InOrder(node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}
用以上程序可以测出是否是红黑平衡树。
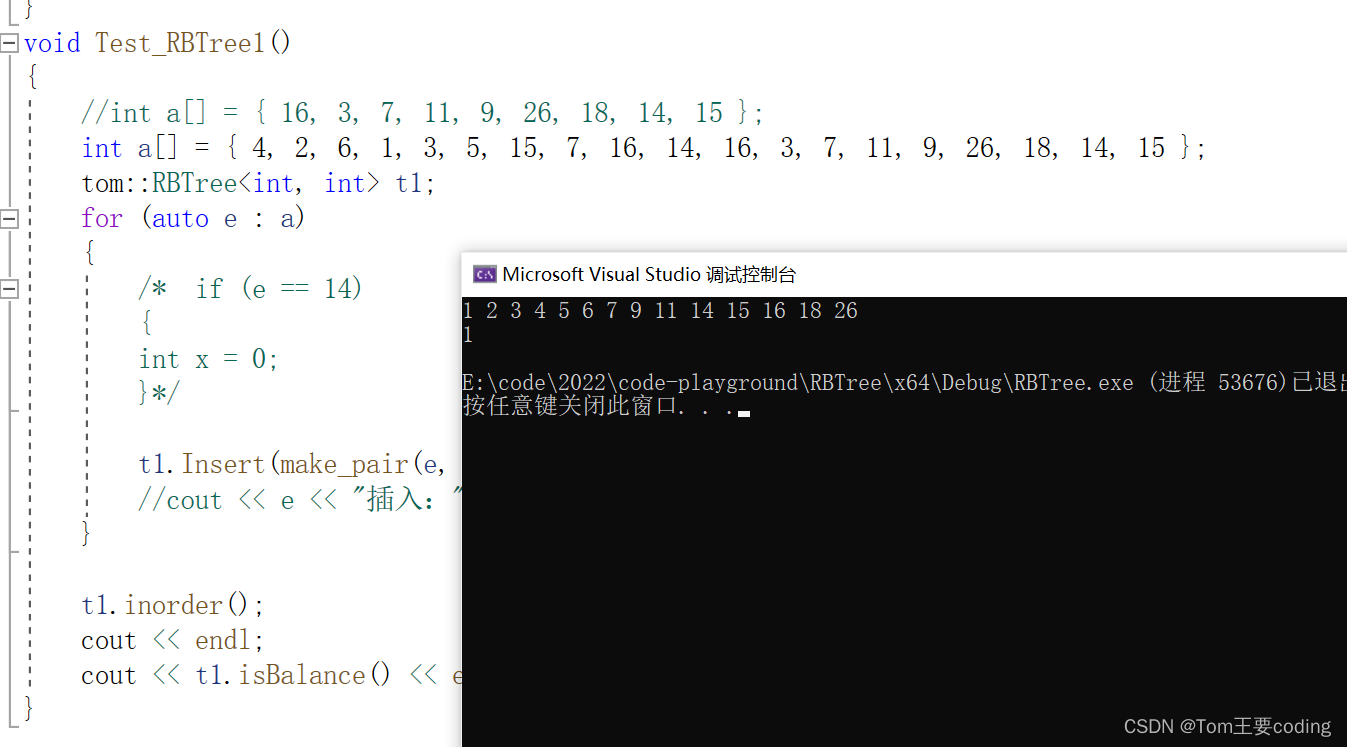
测试结果
void Test_RBTree1()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, 16, 3, 7, 11, 9, 26, 18, 14, 15 };RBTree<int, int> t1;for (auto e : a){/* if (e == 14){int x = 0;}*/t1.Insert(make_pair(e, e));//cout << e << "插入:" << t1.IsBalance() << endl;}t1.InOrder();cout << t1.IsBalance() << endl;
}void Test_RBTree2()
{srand(time(0));const size_t N = 5000000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand()+i;t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}//t.Inorder();cout << t.IsBalance() << endl;cout << t.Height() << endl;
}
相关文章:

C++进阶——红黑树
C进阶——红黑树 概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过 对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩 倍&…...
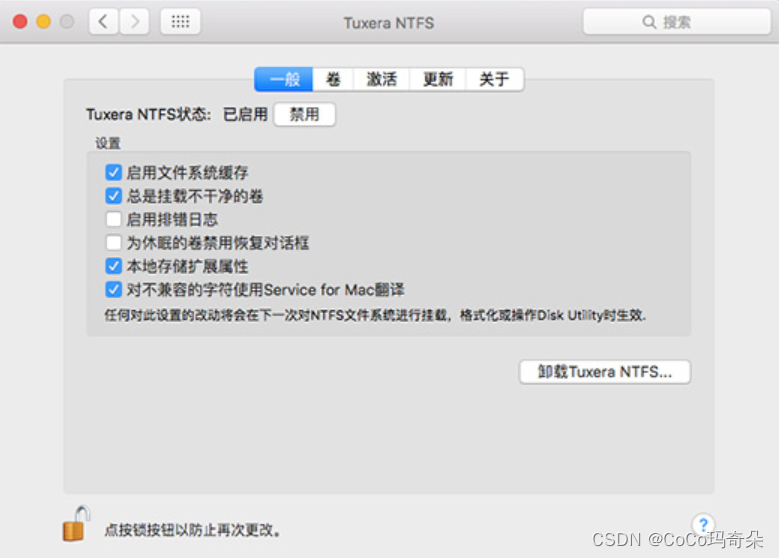
什么是NTFS for Mac?2023新版本如何下载
在NTFS for Mac中包含了多种功能操作,促进软件更好地使用,可以进行全局设置,也可以针对某一各挂载的磁盘进行针对性设置。 本集小编主要向大家介绍它包含的一些基本功能,看看这款mac读写工具能够实现那些功能,全面了解…...

Python泰裤辣丨520写一个自动换壁纸软件,将女友照骗放进去送给她
Python泰裤辣!520写一个自动换壁纸软件,将女友照骗放进去送给她! 准备工作1、环境2、使用的模块3、如何配置pycharm里面的python解释器?4、pycharm如何安装插件? 代码实战1、获取壁纸 自动更换壁纸程序最后 话说兄弟们,今天520你们都送给女朋友啥礼物了…...

CMake: 设置编译选项
CMake: 设置编译选项 导言编译器选项相关概念编译器选项设置补充 导言 上一篇我们学习了构建类型的相关内容,并且可以生成了不同构建类型的库,这一篇我们将介绍编译器选项的相关内容。 编译器选项相关概念 编译器选项是指在编译程序时,可以…...
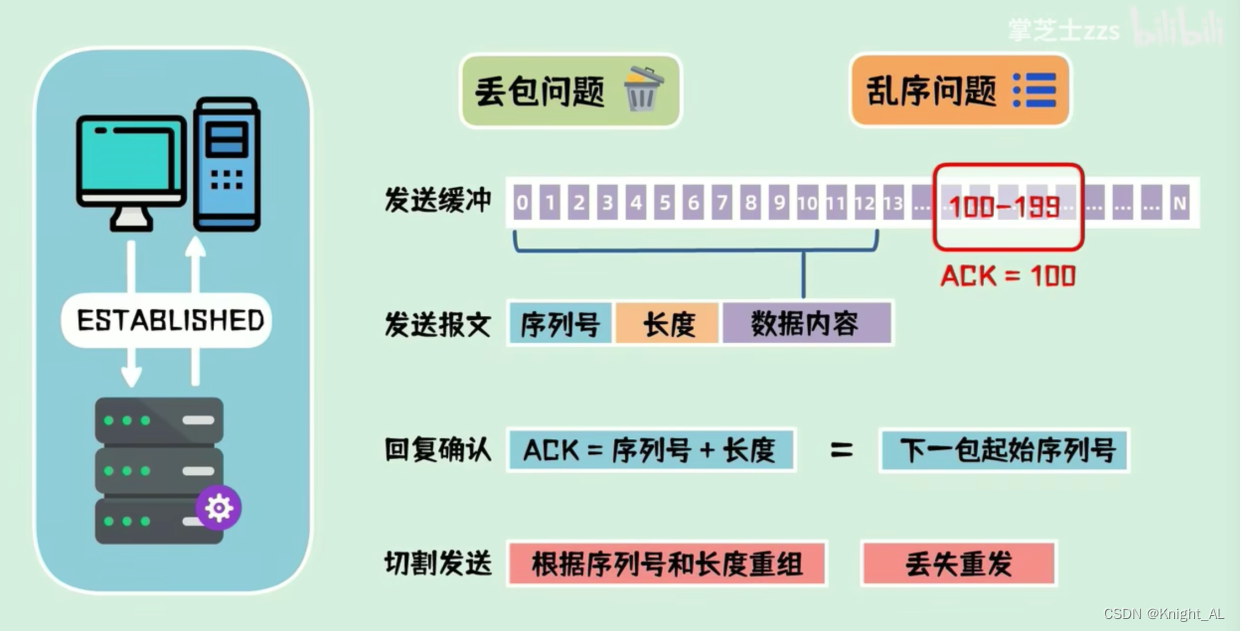
美团Java开发一面凉经
目录 1.HashMap底层数据结构2.列举几个常见的线程安全容器3.HashMap线程问题4.concurrentHashMap5.ConcurrentModificationException6.Spring AOP、IOC、DI介绍下7.不使用依赖注入,使用传统方式的声明会有什么问题8.最左前缀原则9.TCP三次握手、四次挥手 1.HashMap底…...
-spring面试知识点二)
Java面试知识点(全)-spring面试知识点二
Java面试知识点(全) 导航: https://nanxiang.blog.csdn.net/article/details/130640392 注:随时更新 Spring 事物 事务简介: 事务管理是企业级应用程序开发中必不可少的技术,用来确保数据的完整性和一致性 事务就是一系列的动作&…...
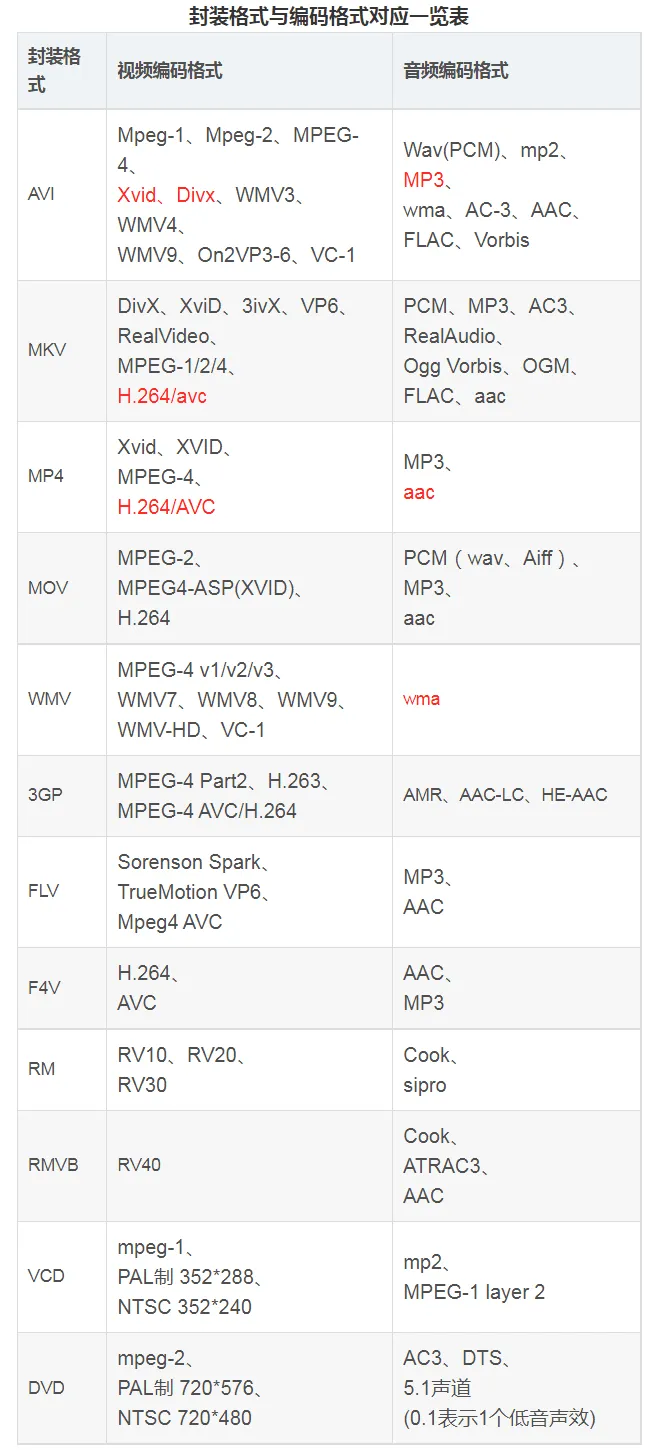
【音视频开发】基础知识:视频封装格式和编码格式
文章目录 一、封装格式与编码格式的关系视频编码格式视频封装格式MP43GPRM、RMVBAVI、WMVVOBFLVMKVWebMMOVTS 封装格式与编码格式对应 一、封装格式与编码格式的关系 视频编码格式和视频封装格式的关系及区别 这两者的关系好比酒与酒瓶的关系,编码格式好比酒瓶里的…...

OData Web API 一个开放标准的协议
OData Web API 是一个开放标准的协议,用于创建和使用基于 RESTful 的 Web API。它允许开发人员通过统一的方式来发布、查询、操作和管理数据资源。 OData Web API 基于 OData 协议,该协议定义了一组规范和约定,用于建立与数据源交互的标准化…...
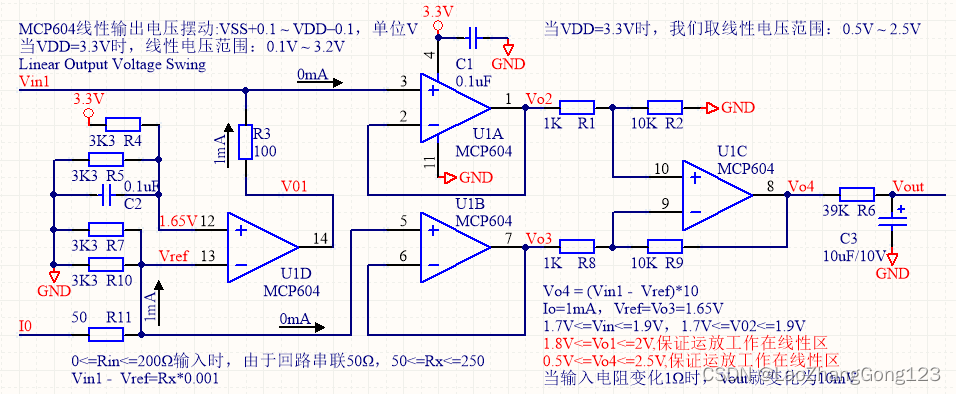
PT100温度采集
1、信号采集的基本原理 PT100是将温度信号转换为电阻输出,其电阻值变化范围为0~200Ω。AD转换器只能对电压进行转换,无法采集直接采集温度,因此,需要一个1mA恒电流源给PT100供电,将电阻变化转换为电压变化。使用恒流源…...
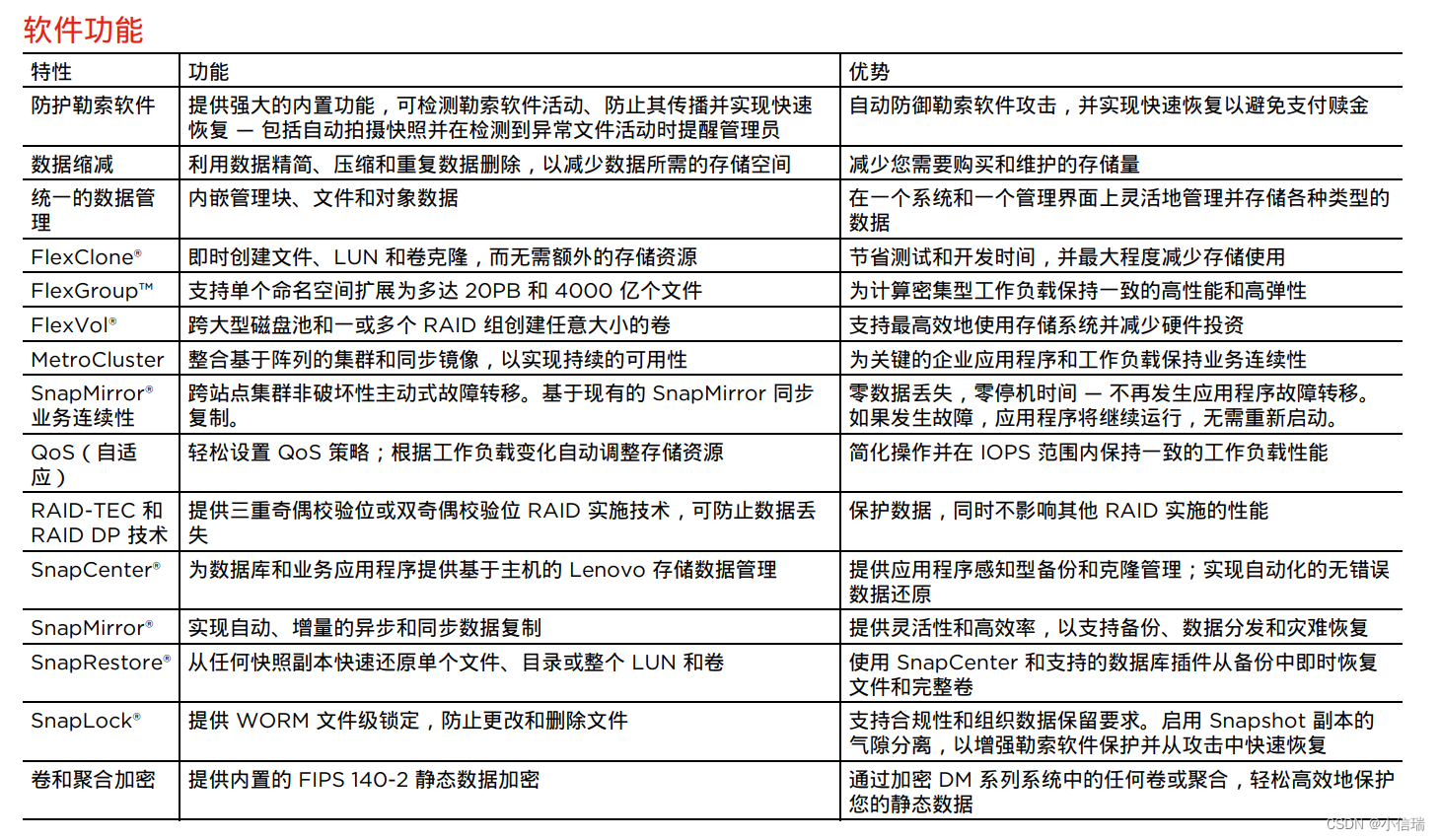
ThinkSystem DM 全闪存阵列 —— 通过全闪存 NVMe 转型加速您的业务
ThinkSystem DM 全闪存阵列——通过全闪存 NVMe 转型加速您的业务 挑战 要缩短产品上市时间并提高客户满意度,企业必须不断改善关键业务运营的速度和响应能力。其中的一个关键要素是全闪存存储,它可以大幅加速关键工作负载。 不过,随着全闪…...
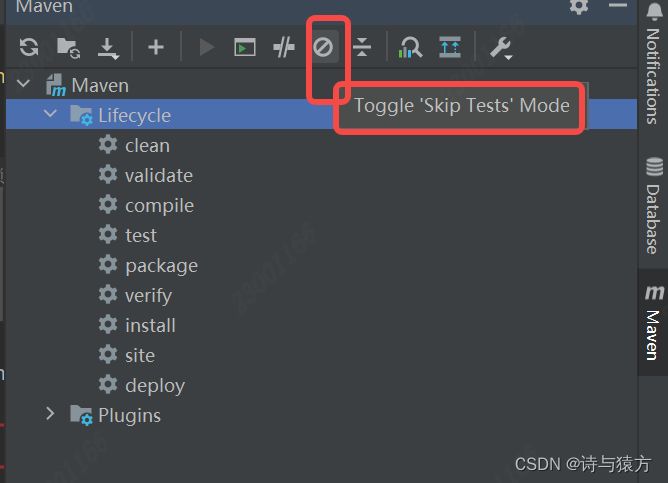
SpringCloud------代码demo(二)
SpringCloud------代码demo(二) 编码实操 以订单——支付微服务模块作为基础,开始逐渐扩充 微服务架构编码构建 1.约定 > 配置 > 编码 2.IDEA新建project工作空间 3.Rest微服务工程构建 总父工程 POM project module 首先创建maven项…...

TCL语法
目录 脚本、命令和单词符 置换 变量置换 命令置换 反斜杠置换 双引号和花括号 注释 脚本、命令和单词符 一个 TCL 脚本可以包含一个或多个命令。命令之间必须用换行符或分号隔开。 set a 1 set b 2 或者 set a 1;set b 2 都是合法的 TC…...
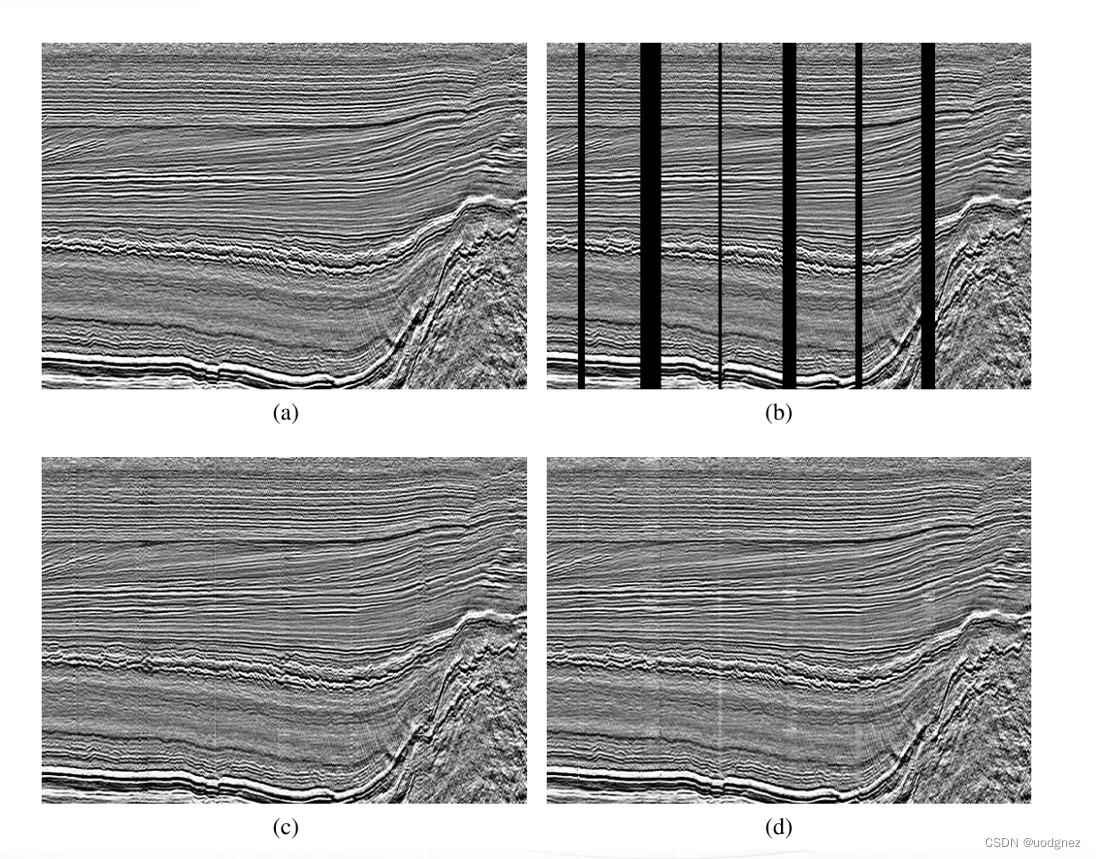
Partial convolution Gated convolution
组会讨论帖 1. 图像修复 图像修复(Image Inpainting),顾名思义,就是将图像中损坏的部分修复起来,是一种图像编辑技术,可以应用在移除物体、修复老照片、图像补全(eg,地震插值)等等。…...
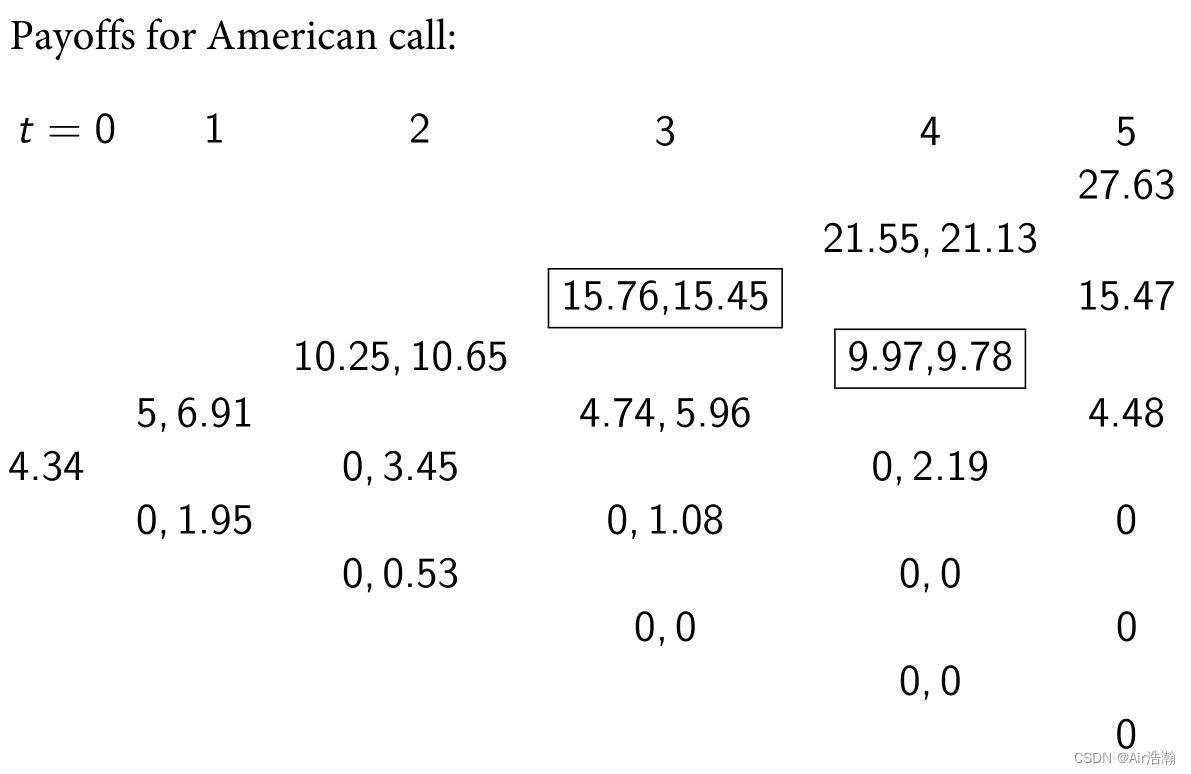
量化投资 无套利 No-arbitrage
文章目录 量化投资 无套利 No-arbitrageState of Nature市场域 Market Span 套利 Arbitrage无套利和正线性定价规则 No-arbitrage and Positive Linear Pricing RuleImplication 1: One-price PrincipleImplication 2: PositivityImplication 3: AdditivityImplication 4: Homo…...

小程序容器助力智能移动门户统一
智能移动统一门户遵循“统一规划,统一标准,统一建设,统一运维”的指导思想。它灵活运用前端展示平台,微服务后端平台,流程引擎,规则引擎,非结构化数据平台,即时通讯平台,…...

opencv-python相机标定详解
文章目录 角点检测查看角点标定 opencv中内置了张正友的棋盘格标定法,通过一些姿态各异的棋盘格图像,就能标定相机的内外参数。 角点检测 第一步是角点检测,首先需要读取棋盘格图像 import numpy as np import cv2 import ospath imgs #…...

由斯坦福、Nautilus Chain等联合主办的 Hackathon 活动,现已接受报名
由 Stanford Blockchain Accelerator、Zebec Protocol、 Nautilus Chain、Rootz Lab 共同主办的黑客松活动,现已接受优秀项目提交参赛申请。 在加密行业发展早期,密码极客们就始终在对区块链世界基础设施,在发展方向的无限可能性进行探索。而…...
)
PBDB Data Service:Measurements of specimens(标本测量)
Measurements of specimens(标本测量) 描述参数以下参数可用于指定您感兴趣的标本种类以下参数可用于筛选所选内容以下参数还可用于根据分类筛选结果列表以下参数可用于生成数据存档您可以使用以下参数选择要检索的额外信息,以及要获取记录的…...
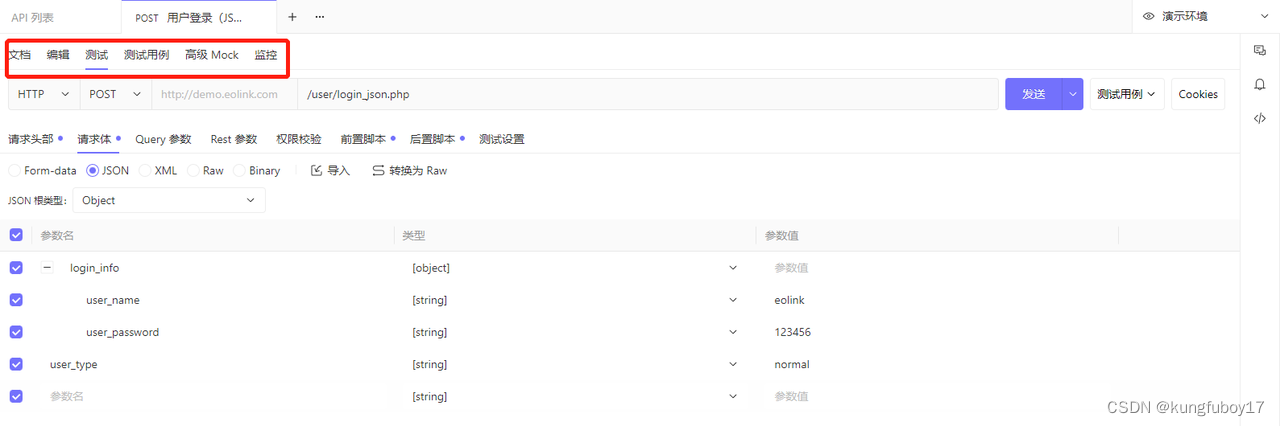
低调的接口工具 ApiKit
最近发现一款接口测试工具--ApiKit,我们很难将它描述为一款接口管理工具 或 接口自测试工具。 官方给了一个简单的说明,更能说明 Apikit 可以做什么。 ApiKit API 管理 Mock 自动化测试 异常监控 团队协作 ApiKit的特点: 接口文档定义&a…...
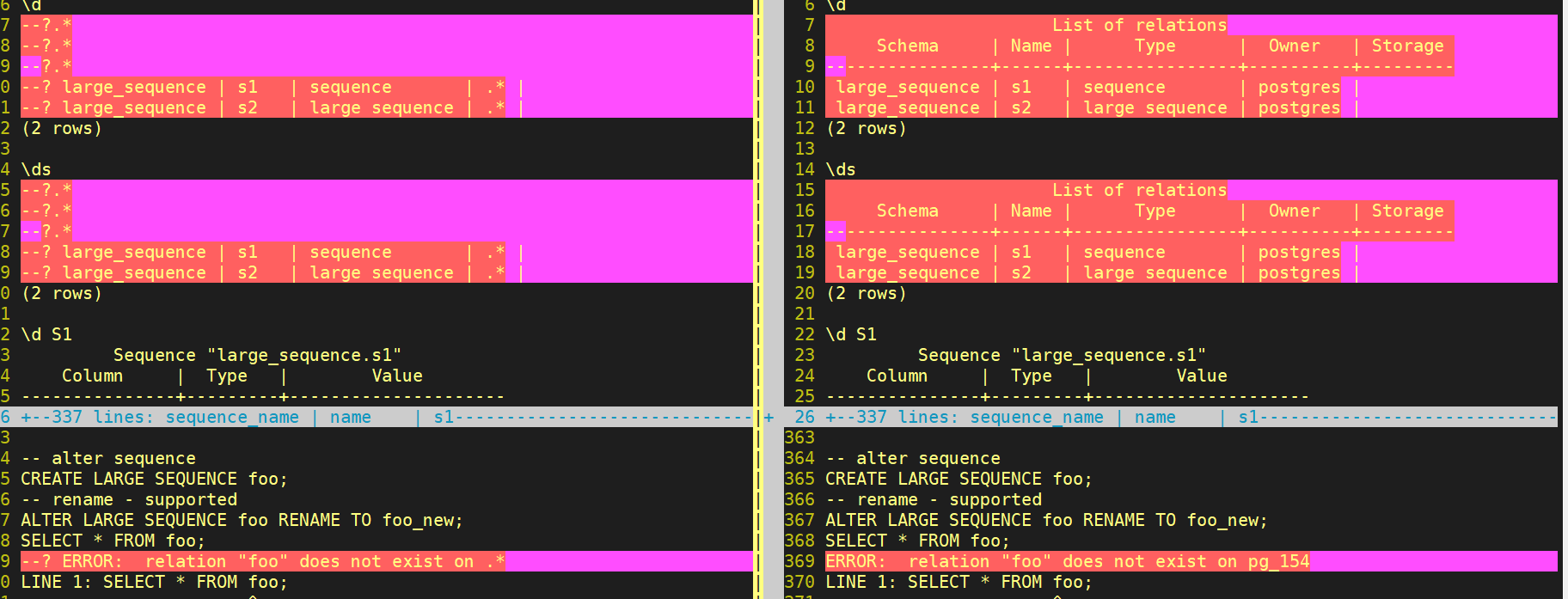
opengauss 的回归测试
目录 一、回归测试说明 二、单独执行测试用例(开发调试) 一、回归测试说明 opengauss/postgresql 的回归测试,通过执行SQL比较输出打印,判断代码修改是否改变了其它功能逻辑。 OG的回归测试大体上和PG类似,主要是通…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
