什么是Dirichlet分布?
Dirichlet分布是一种概率分布,用于描述多维随机变量的概率分布。它是一个连续分布,通常用于处理具有多种可能取值的离散型随机变量。在LDA模型中,Dirichlet分布通常被用作先验分布,用来表示主题的概率分布和单词的概率分布。
Dirichlet分布的概率密度函数如下所示:
Dirichlet ( α ) = 1 B ( α ) ∏ i = 1 k x i α i − 1 \text{Dirichlet}(\alpha) = \frac{1}{B(\alpha)}\prod_{i=1}^k x_i^{\alpha_i-1} Dirichlet(α)=B(α)1i=1∏kxiαi−1
其中, k k k 为维度, α \alpha α 为 k k k 维向量, x x x 为满足 x i ∈ [ 0 , 1 ] x_i \in [0,1] xi∈[0,1]且 ∑ i = 1 k x i = 1 \sum_{i=1}^k {x_i} = 1 ∑i=1kxi=1 的 k k k 维向量。 B ( α ) B(\alpha) B(α) 是常数项,满足以下公式:
B ( α ) = ∏ i = 1 k Γ ( α i ) Γ ( ∑ i = 1 k α i ) B(\alpha) = \frac{\prod_{i=1}^k \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^k \alpha_i)} B(α)=Γ(∑i=1kαi)∏i=1kΓ(αi)
Γ ( n ) \Gamma(n) Γ(n) 表示 gamma 函数,通常表示成 Γ ( n ) = ( n − 1 ) ! \Gamma(n)=(n-1)! Γ(n)=(n−1)!。对于参数 α \alpha α,在LDA模型中常被视为一个超参数,控制着生成模型中未知参数的分布,影响模型的结果和效果。根据 Dirichlet 分布的性质, α \alpha α 越大,对应的主题分布或单词分布越平滑,相反, α \alpha α 越小,分布的区分度也越高。
相关文章:

什么是Dirichlet分布?
Dirichlet分布是一种概率分布,用于描述多维随机变量的概率分布。它是一个连续分布,通常用于处理具有多种可能取值的离散型随机变量。在LDA模型中,Dirichlet分布通常被用作先验分布,用来表示主题的概率分布和单词的概率分布。 Dir…...

web前端开发需要哪些技术?学前端顺序千万千万不要搞错啦!
宝子们,下午好,之前给大家分享了前端岗位的前景规划,小源看的出来,还是有不少宝子想入行前端的! 那除了会面试,还要有充足丰富的知识储备,需要什么技术,怎么样做才能找到高薪工作呢&…...

【AFNetWorking源码(二)AFURLSessionManger和AFHTTPSessionManager】
前言 学习了Mananger的初始化和以GET请求为例的过程,发现整个过程离不开AFHTTPSessionManager和AFURLSessionManger的某些方法。这两个是AFN的重要的网络通信模块内容,对它们作揖详细的学习。 AFURLSessionManager和AFHTTPSessionManager都是AFNetwork…...
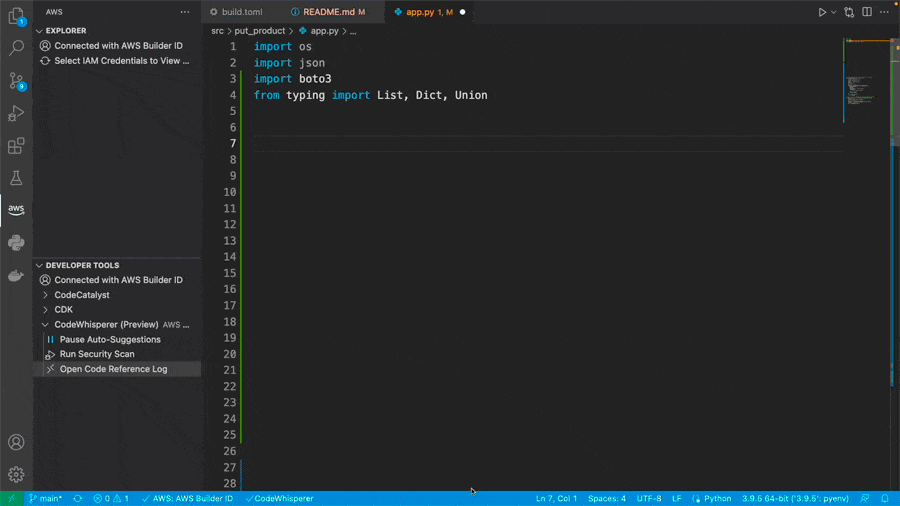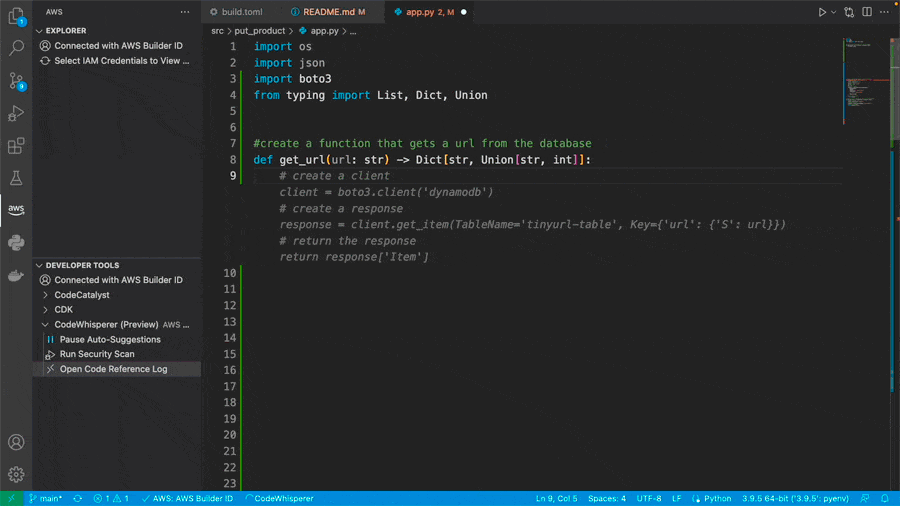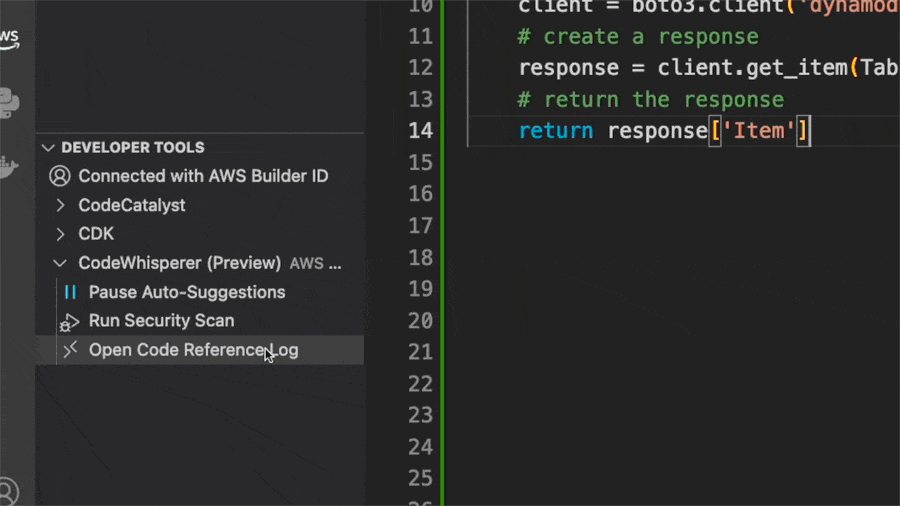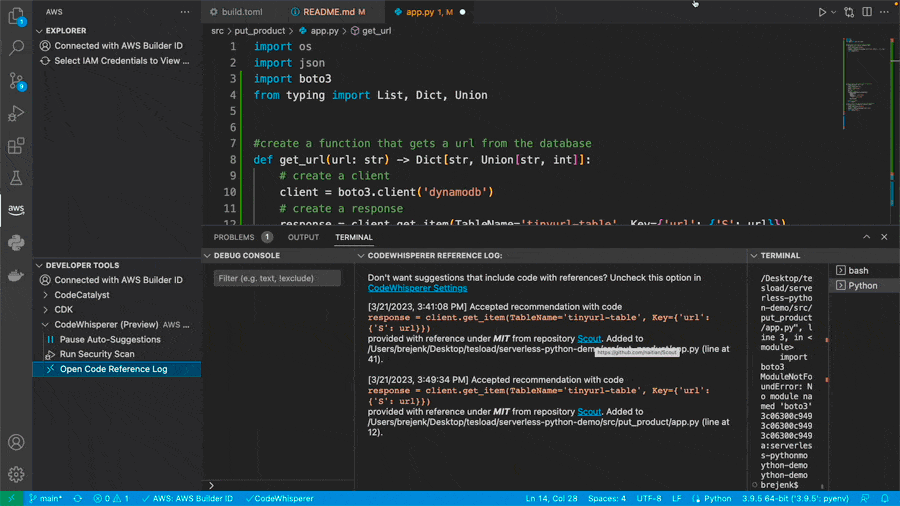
编程不头秃,Google「AI程序员」来了,聊天就能敲代码
上周 Google 在 I/O 大会宣布了一个能够辅助编程的聊天机器人 Codey,现在它终于上线 Google Colab 啦! 🌟 Codey 是基于 Google 目前最新的大语言模型 PaLM 2 运行,有着强大的语言理解和编程能力。 Codey 有这些功能࿱…...
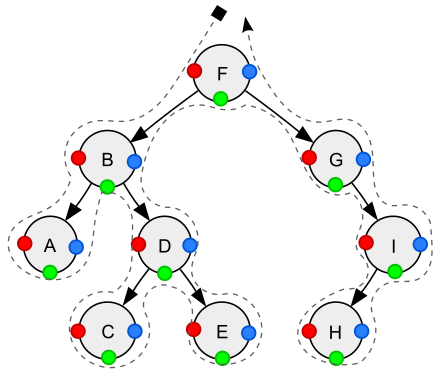
【数据结构与算法】基础数据结构
文章目录 数组概述动态数组二维数组局部性原理越界检查 链表概述单向链表单向链表(带哨兵)双向链表(带哨兵)环形链表(带哨兵) 队列概述链表实现环形数组实现 栈概述链表实现数组实现应用 双端队列概述链表实…...

k8s系列(四)——资源对象
k8s系列四——资源对象 pod概念 思考:为什么k8s会引出pod这个概念,容器不能解决么? 我的理解:一组密切相关的服务使用容器的话,如果他们的镜像不在一个容器里的话,那么就需要配置反向代理进行通信…...

JavaScript如何使用for循环
JavaScript 是一门非常有趣的编程语言,它可以让我们在浏览器中创建交互式的 Web 应用程序。在 JavaScript 中,我们可以使用 for 循环来迭代一个数组或对象,从而执行一系列的操作。下面是一些关于 for 循环的有趣的用法和例子。 为什么要使用…...
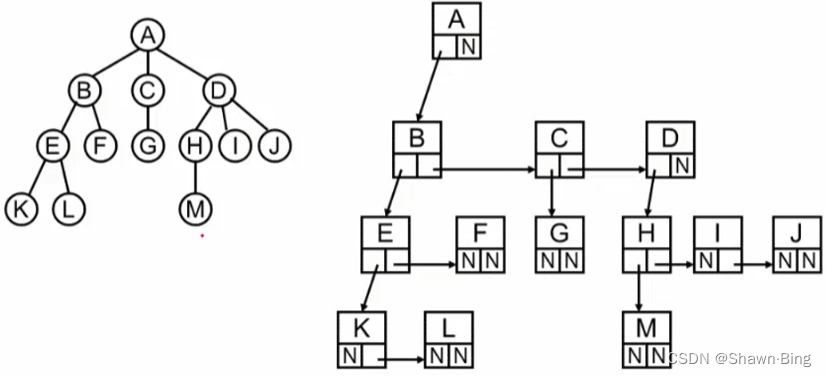
(浙大陈越版)数据结构 第三章 树(上) 3.1 树和树的表示
目录 3.1.1 引子(顺序查找) 什么是树 查找 3.1.2 引子 二分查找例子(BinarySearch) 二分查找 3.1.3 引子 二分查找实现 二分查找代码 二分查找的启示 3.1.4 树的定义 一些基本术语: 3.1.5 树的表示 3.1.1 引子(顺序查找…...

平抑风电波动的电-氢混合储能容量优化配置(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

#机器学习--重新看待线性回归
#机器学习--重新看待线性回归 引言普通视角的线性回归最大似然角度的线性回归总结 引言 本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简,适合二次学习的读者快速学习或查阅。 普通视角的线性回归 对于一组数据 { ( x 0 , y 0 ) , … ( x m…...

亚马逊,shopee,lazada卖家如何组建自己的测评团队
测评补单,这个话题在如今不管国内还是国外的电商行业已经是众所周知,它能够快速帮助自己的产品添加评论,获取排名,打造爆款,可以让用户更加真实、清晰、快捷的了解产品,以及产品的使用,快速上手…...

flink cdc 用mybatis-plus写到mysql5.6
背景 项目中需要做一个数据同步的功能, 在方案对比中,canal 与flink cdc 都有尝试。 起初在网上找的flink例子,要么只能支持mysql5.7以上版本,要么就是需要序列化各种bug,比如就不能直接使用 @Autowired xxxServer 来调用数据库层面的注入,getBaseMapper()为空 因为目…...
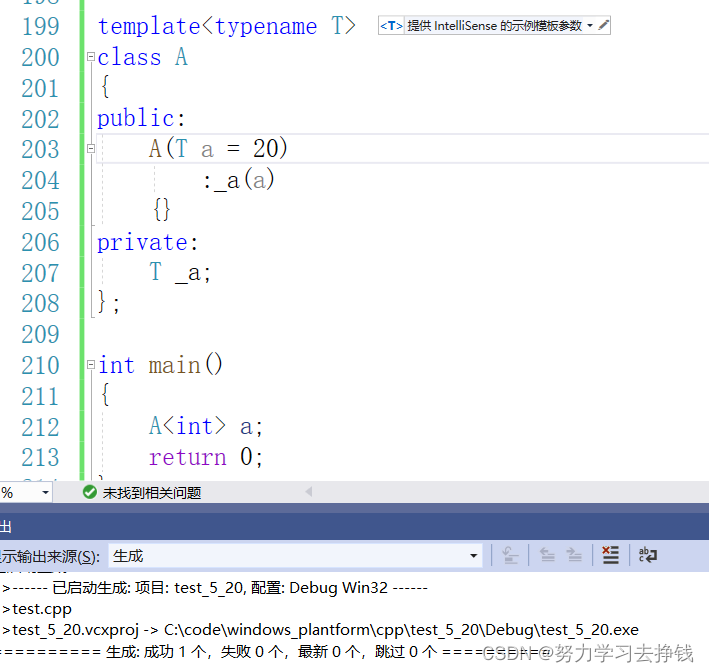
【C++】模板的一点简单介绍
模板 前言泛型编程函数模板概念格式函数模板的原理函数模板的实例化 类模板类模板的定义格式类模板的实例化 前言 这篇博客讲的是模板的一些基本知识,并没有那么深入,但是如果你是为了过期末考试而搜的这篇博客,我觉得下面讲的是够了的。 之…...
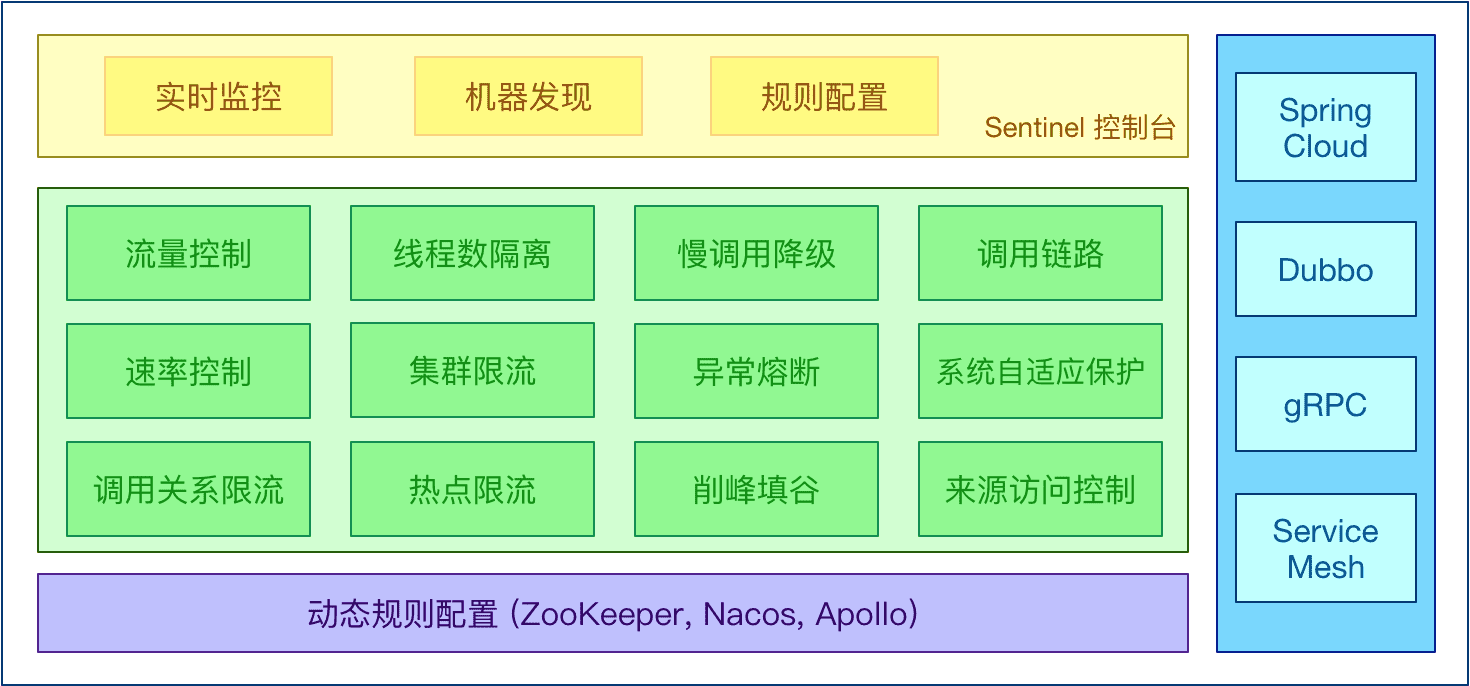
SpringCloud概述
前言 什么是微服务? 微服务是一种面向服务的架构(SOA)风格,其中,应用程序被构建为多个不同的小型服务的集合而不是单个应用程序。与单个程序不同的是,微服务让你可以同时运行多个独立的应用程序,而这些独立的应用…...

Metal入门学习:GPU并行计算大数组相加
一、编程指南PDF下载链接(中英文档) 1、Metal编程指南PDF链接 https://github.com/dennie-lee/ios_tech_record/raw/main/Metal学习PDF/Metal 编程指南.pdf 2、Metal着色语言(Metal Shader Language:简称MSL)编程指南PDF链接 https://github.com/dennie-lee/ios_te…...

关于在spyder,jupyter notebook下创建虚拟环境(pytorch,tensorflow)均有效
anaconda下载地址 https://www.anaconda.com/download/ 下载完成后打开anaconda目录下的 anaconda prompt 在命令行中输入下面的命令创建一个叫tf2.0的虚拟环境(“tf2.0”是建立的Conda虚拟环境的名字,可以自拟) conda create -n tf2.0 p…...

oracle 闪回恢复
oracle 闪回恢复 闪回恢复区主要通过3个初始化参数来设置和管理: db_recovery_file_dest:指定闪回恢复区的位置 db_recovery_file_dest_size:指定闪回恢复区的可用空间大小 db_flashback_retention_target:指定数据库可以回退的时…...

LeetCode 322 零钱兑换
题目: 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量…...

面试篇SpringMVC是什么以及工作原理
1,什么是SpringMVC呢? 它是Spring的一种设计模式,一款框架。 2,MVC分别代表什么? M代表模型即model的缩写,指业务逻辑层模型。V代表视图即View的缩写,指视图层。C则是controller的缩写ÿ…...

jQuery-层级选择器
<!DOCTYPE HTML> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"> <title>层级选择器</title> <style type"text/css"> …...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
