【离散数学】置换群和伯恩赛德定理编程题
1:置换的轮换表示
给出一个置换,写出该置换的轮换表示。比如
(1 2 3 4 5 6 7 8 9)
(3 1 6 2 9 7 8 4 5)
表示为(1 3 6 7 8 4 2)(5 9)
输入:
置换后的序列
输出:
不相杂的轮换乘积,每行表示一个轮换(轮换的起始数字最小,每个轮换的起始数字递增排序,单轮换省略)
例如:
样例1:
输入:(空格分隔)
3 1 6 2 9 7 8 4 5
输出:
1 3 6 7 8 4 2(空格分隔)
5 9(空格分隔)
样例2:
输入:(空格分隔)
4 6 7 5 1 2 3
输出:
1 4 5(空格分隔)
2 6(空格分隔)
3 7 (空格分隔)
#include <cstdio>
#include <cstring>
int main()
{char c[50];gets(c); int n=(strlen(c)+1)/2;int i,j=0,k,flag=1,a[25],b[25];for(i=0;i<n;i++){a[i]=c[2*i]-48;b[i]=0;}int l=1;b[j]=l;printf("%d ",b[j]);j++;for(i=0;j<n;){if(a[i]==l) //a[i]等于这一轮换的头,说明轮换结束 {printf("\n"); l++; //找下一个轮换的头while(flag==1){for(k=0;k<j;k++){ if(l==b[k]) //l不能已经在之前的轮换中 {break;}}if(k==j) //l不在轮换里 {if(l==a[l-1]) //单轮换不输出,还要接着找头不改变flag跳出while循环{b[j]=l;j++; if(j==n) //如果单轮换是最后的数,就不用再找了,跳出while循环 {flag=0;}} else //找到l了,可以跳出while循环{flag=0; b[j]=l;printf("%d ",b[j]);j++;i=l-1;} }else{l++;}}flag=1; //给下一次找头做准备 }else //a[i]不等于轮换的头 就继续加到轮换里{b[j]=a[i];printf("%d ",b[j]);j++;i=a[i]-1;}}return 0;
} 2:轮换的复合运算
集合S中的元素个数小于10个,输入该集合的两个轮换t1和t2,计算两个轮换的乘积t(乘积采用左复合),输出的乘积结果t也表示为轮换。输入时每行输入一个不相交轮换ti(i=1,2),输出的乘积为不相交轮换(单轮换省略不写)。
样例1:
输入: (注:数字和括号之间都没有空格,括号“(”和")"为半角英文)
(123)(456) (注:t1)
(245) (注:t2)
输出:
(1253)(46) (注:乘积t的每个轮换的起始数字是递增排序)
样例2:
输入: (注:数字和括号之间都没有空格,括号“(”和")"为半角英文)
(16)(23) (45)
(36)(125)
输出:
(13)(2456) (注:每个轮换的起始数字是递增排序)
样例3:
输入: (注:数字和括号之间都没有空格,括号“(”和")"为半角英文)
(2654)
(15)
输出:
(14265) (注:每个轮换的起始数字是递增排序)
样例4:
输入: (注:数字和括号之间都没有空格,括号“(”和")"为半角英文)
(1392)(475)
(267)
输出:
(13926547) (注:每个轮换的起始数字是递增排序)
#include <iostream>
#include <cstring>
using namespace std;
int b[20];
void work(int a[],int n){int j,i=0,k=0,num=1,count=n-3;printf("(1");int b[10]={0};while(k<count-1){if(a[i]!=i+1)printf("%d",a[i]);b[i]=1;k++;i=a[i]-1;if(a[i]==num){b[i]=1;k++;for(j=0;j<count-1;j++){if(b[j]==0){i=j;num=j+1;if(num!=a[i])printf(")(%d",num);break;}}}}printf(")");
}int main()
{char x[20],y[20];gets(x);gets(y);int i,j,k;int num1=0,num2=0,e=0,r=0;int count=0;int z[20]={0};for(i=1;i<11;i++) //从1开始 {for(j=0;j<strlen(y);j++) //处理下面的轮换 {if(y[j]-'0' == i && y[j+1]!=')') //不等于末尾数 {num1=y[j+1]-'0';break;}if(y[j]-'0'==i && y[j+1]==')') //等于末尾数 {int m=0;for(m=j;m>=0;m--){ if(y[m]=='(') //找到该轮换的第一个数 {num1=y[m+1]-'0';e=1;break;}}if(e==1){break;}}num1=i; //未找到这个数,即等于自身。 }for(k=0;k<strlen(x);k++){if(x[k]-'0'==num1 && x[k+1]!=')') //不等于末位数 {num2=x[k+1]-'0';break;};if(x[k]-'0'==num1 && x[k+1]==')'){int m=0; for(m=k;m>=0;m--){if(x[m]=='('){num2=x[m+1]-'0';r=1;break;}}if(r==1){break;}};num2=num1;}e=0;r=0;z[count]=num2; count++;}work(z,count);
}
/*
int main(){char c[50];gets(c);char b[50];gets(b); int i,j,k,num1=0,num2=0,e=0,r=0,count=0;int arr[50]={0};for(i=1;i<11;i++){//start from 1for(j=0;j<strlen(b);j++){if(b[j]-'0'==i && b[i+1]!=')'){//非末尾的映射num1=b[j+1]-'0';break; } else if(b[j]-'0'==i && b[i+1]==')'){//末尾的映射int t;for(t=j;t>=0;t--){if(b[t]=='('){//轮换的第一个数num1=b[t+1]-'0';e=1;break; }}if(e==1){break;}}num1=i;//not found}for(k=0;k<strlen(c);k++){if(c[k]-'0'==num1 && c[k+1]!=')'){num2=c[k+1]-'0';break;}else if(c[k]-'0'==num1 && c[k+1]==')'){int t=0;for(t=k;t>=0;t--){if(c[t]=='('){num2=c[t+1]-'0';r=1;break;}}if(r==1){break;}}num2=num1;}e=0;r=0;arr[count++]=num2;}//arr [] , countcout<<("(1");int ret[10]={0};i=0;j=0;k=0;int n=count-3,num=1;while(k<n-1){if(arr[i]!=i+1){cout<<arr[i];}ret[i]=1;k++;i=arr[i]-1;if(arr[i]==num){ret[i]=1;k++;for(j=0;j<n-1;j++){if(ret[j]==0){i=j;num=j+1;if(num!=arr[i]){cout<<")("<<num;break;}}}}}cout<<")";return 0;
}
*/
好像给的案例最多只有两个划分区域
// int len=strlen(c),heap[20],flag=0,cnt=0;
// for(int i=0;i<len;i++){
// if(c[i]=='('){
// flag=1;
// continue;
// }
// else if(c[i]==')'){
// flag=0;
// heap[cnt++]=-1;
// //以-1分割
// }
// //利用flag判断是否进数组
// if(flag==1){
// heap[cnt++]=c[i]-'0';
// }
// }
//
// int lenb=strlen(b),heapb[20],flagb=0,cntb=0;
// for(int i=0;i<lenb;i++){
// if(b[i]=='('){
// flagb=1;
// continue;
// }
// else if(b[i]==')'){
// flagb=0;
// heapb[cntb++]=-1;
// //以-1分割
// }
// //利用flag判断是否进数组
// if(flagb==1){
// heapb[cntb++]=b[i]-'0';
// }
// }
// for(int i=0;i<cntb;i++){cout<<heapb[i]<<" ";}
//
// int max=-1;
// for(int i=0;i<cnt;i++){
// if(max<heap[i]){
// max=heap[i];
// }
// }
// for(int i=0;i<cntb;i++){
// if(max<heapb[i]){
// max=heapb[i];
// }
// }
// //cout<<max;
//
// //开始映射(?)
// int visit[max+1]={0};//标记是否visited
// visit[0]=1;
// while(1){
//
// }3:脾气牛排队 Cow Sorting
Description
Farmer John's N (1 ≤ N ≤ 10,000) cows are lined up to be milked in the evening. Each cow has a unique "grumpiness" level in the range 1...100,000. Since grumpy cows are more likely to damage FJ's milking equipment, FJ would like to reorder the cows in line so they are lined up in increasing order of grumpiness. During this process, the places of any two cows (not necessarily adjacent) can be interchanged. Since grumpy cows are harder to move, it takes FJ a total of X+Y units of time to exchange two cows whose grumpiness levels are X and Y.
Please help FJ calculate the minimal time required to reorder the cows and give the procedure of sorting.
输入:
第1行:N (整数N代表牛的数量)
第2行到N+1行:牛的脾气值
输出:
第1行:最小排队代价值
第2行:给牛按脾气值升序排列的排队过程(每行表示一对交换,脾气值空格分隔)
样例:
输入:
7
6
7
4
5
3
2
1
输出:
33
6 1 4 5 3 2 7
6 2 4 5 3 1 7
1 2 4 5 3 6 7
1 2 4 3 5 6 7
1 2 3 4 5 6 7
#include <cstdio>
int main()
{int i,j=0,k=1,flag=1,m,n,sum=0;int a[20],b[20],c[20][20];scanf("%d",&n); for(i=0;i<n;i++){scanf("%d",&a[i]);}int t=0,l=1;b[j] = l;j++;c[t][k] = l;k++;for(i=0;j<=n;){if(a[i]==l || j==n) //a[i]等于这一轮换的头,或者b[]满了(所有数都进入了轮换),说明轮换结束{c[t][0] = k; //c的每行第一个元素用来记录这个轮换的阶数+1if(c[t][1]*(k-2) > c[t][1]*2+k) //如果该轮换开头的,最小的数仍然很大(设为big),用big做k-2次对换的代价是big*(k-2),先把1和big进行一次对换,用1去做k-2次兑换后再换回来代价是(1+big)*2+1*(k-2){int big = c[t][1];for(m=0;m<k;m++){ c[t+1][m] = c[t][m]; //把当前轮换往下挪一步}c[t][0] = 3;c[t][1] = 1;c[t][2] = c[t+1][1]; //加入一行轮换(对换) 把1和开头换一次c[t+1][1] = 1; //把1换成该轮换的开头 sum += 1+big;t++;for(k--;k>1;k--){ sum += c[t][1]+c[t][k]; //代价加上对换的两个数}t++; c[t][0] = 3;c[t][1] = big;c[t][2] = 1; //再加入一行轮换(对换) 把1和开头换回来sum += 1+big;}else{for(k--;k>1;k--) //每个轮换都会被拆成k-1个对换{ sum += c[t][1]+c[t][k]; //代价加上对换的两个数} } t++;l++;while(flag==1){for(m=0;m<j;m++){ if(l==b[m]){break; //l不能已经在之前的轮换中 }}if(m==j) //l不在轮换里 {if(l==a[l-1]){ b[j] = l;j++; //单轮换不输出,还要接着找头不改变flag跳出while循环 if(j==n){flag = 0; //如果单轮换是最后的数,就不用再找了,跳出while循环 } } else{flag = 0; b[j] = l;j++;c[t][k] = l;k++;i = l-1;} }else{l++;}}flag=1; //给下一次找头做准备}else{ b[j] = a[i];j++; //b记录出现在所有轮换里的数 c[t][k] = a[i];k++; //c记录每一次轮换里的数 i = a[i]-1;}} printf("%d\n",sum);j=t;for(t=0;t<j;t++) //把每个轮换c[t]拆成c[t][0]-1个对换{ for(k=c[t][0]-1;k>1;k--) //对换c[t][1]和c[t][k]所代表的数在a[]中的位置{int x,y; //x表示c[t][1]代表的数的位置;y表示c[t][k]代表的数的位置for(x=0;x<n;x++){if(a[x]==c[t][1]){break;}}for(y=0;y<n;y++){if(a[y]==c[t][k]){break;}}int t = a[y];a[y] = a[x];a[x] = t;for(m=0;m<n;m++) //输出此次对换结果{printf("%d ",a[m]);} printf("\n");}} return 0;
}4:洗牌机问题
Description
Alice and Bob have a set of N cards labelled with numbers 1 ... N (so that no two cards have the same label) and a shuffle machine. We assume that N is an odd integer.
The shuffle machine accepts the set of cards arranged in an arbitrary order and performs the following operation of double shuffle : for all positions i, 1 <= i <= N, if the card at the position i is j and the card at the position j is k, then after the completion of the operation of double shuffle, position i will hold the card k.
Alice and Bob play a game. Alice first writes down all the numbers from 1 to N in some random order: a1, a2, ..., aN. Then she arranges the cards so that the position ai holds the card numbered ai+1, for every 1 <= i <= N-1, while the position aN holds the card numbered a1.
This way, cards are put in some order x1, x2, ..., xN, where xi is the card at the ith position.
Now she sequentially performs S double shuffles using the shuffle machine described above. After that, the cards are arranged in some final order p1, p2, ..., pN which Alice reveals to Bob, together with the number S. Bob's task is to guess the order x1, x2, ..., xN in which Alice originally put the cards just before giving them to the shuffle machine.
Input
The first line of the input contains two integers separated by a single blank character : the odd integer N, 1 <= N <= 1000, the number of cards, and the integer S, 1 <= S <= 1000, the number of double shuffle operations.
The following N lines describe the final order of cards after all the double shuffles have been performed such that for each i, 1 <= i <= N, the (i+1)st line of the input file contains pi (the card at the position i after all double shuffles).
Output
The output should contain N lines which describe the order of cards just before they were given to the shuffle machine.
For each i, 1 <= i <= N, the ith line of the output file should contain xi (the card at the position i before the double shuffles).
样例1:
输入:
7 4
6
3
1
2
4
7
5
输出:
4
7
5
6
1
2
3
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define N 1003
using namespace std; int n,m;
int cnt[N],a[N],ans[N],l[N],use[N],b[N]; int main(){ scanf("%d%d",&n,&m); int maxn=0;int j,i;for(i=1;i<=n;i++){scanf("%d",&a[i]),cnt[i]=a[i];} bool flag=1; int t=0;while(1){t++;for(i=1;i<=n;i++){b[i]=a[a[i]];}for(i=1;i<=n;i++){if(cnt[i]!=b[i]) {flag=false;break;}}if(flag){break;}flag=true;for(int i=1;i<=n;i++){a[i]=b[i];}}for(i=1;i<=n;i++){a[i]=b[i];}t=t-m%t;for(i=1;i<=t;i++){for(j=1;j<=n;j++){b[j]=a[a[j]];}for(j=1;j<=n;j++){a[j]=b[j];}}for(i=1;i<=n;i++){printf("%d\n",a[i]);}return 0;
} 相关文章:

【离散数学】置换群和伯恩赛德定理编程题
1:置换的轮换表示 给出一个置换,写出该置换的轮换表示。比如 (1 2 3 4 5 6 7 8 9) (3 1 6 2 9 7 8 4 5) 表示为(1 3 6 7 8 4 2)(5 9) 输入: 置换后的序列 输出: 不相杂的轮换乘积,每行表示一个轮换(轮换的起…...
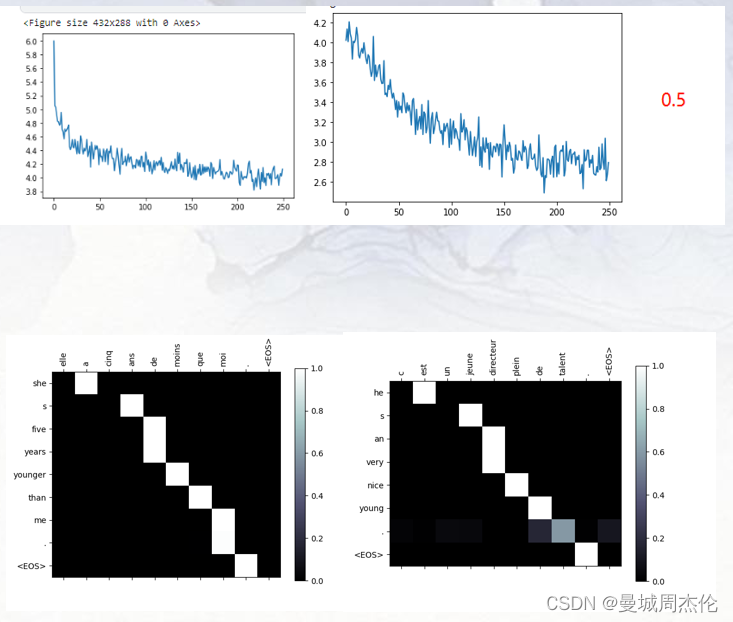
【自然语言处理】 - 作业2: seq2seq模型机器翻译
课程链接: 清华大学驭风计划 代码仓库:Victor94-king/MachineLearning: MachineLearning basic introduction (github.com) 驭风计划是由清华大学老师教授的,其分为四门课,包括: 机器学习(张敏教授) , 深度学习(胡晓林教授), 计算…...
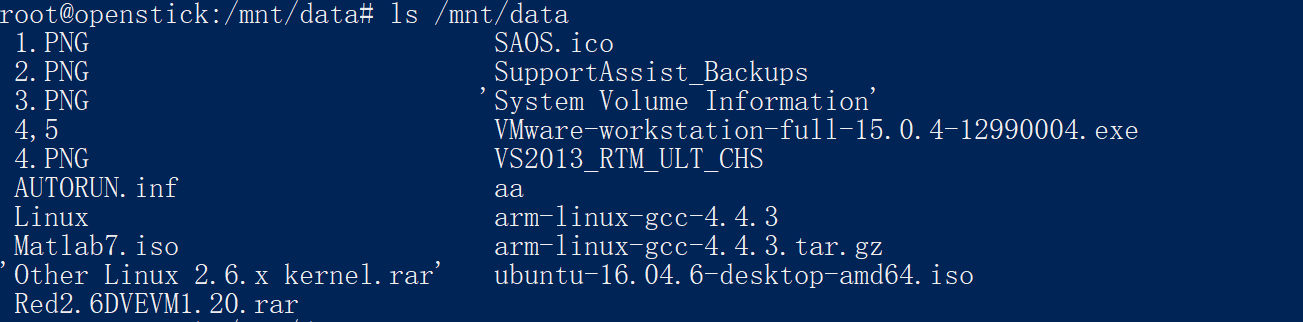
随身WIFI折腾日记(四)---拓展USB接口读取U盘内容
五、USB行为控制 随身WIFI对外交互的接口只有WIFI和USB接口。如果要想接入其他硬件设备,拓展USB接口至关重要,对于USB接口的控制,参考如下链接: openstick项目官方教程:控制usb行为 HandsomeMod/gc: A Simple Tool To Control Usb Gadget …...
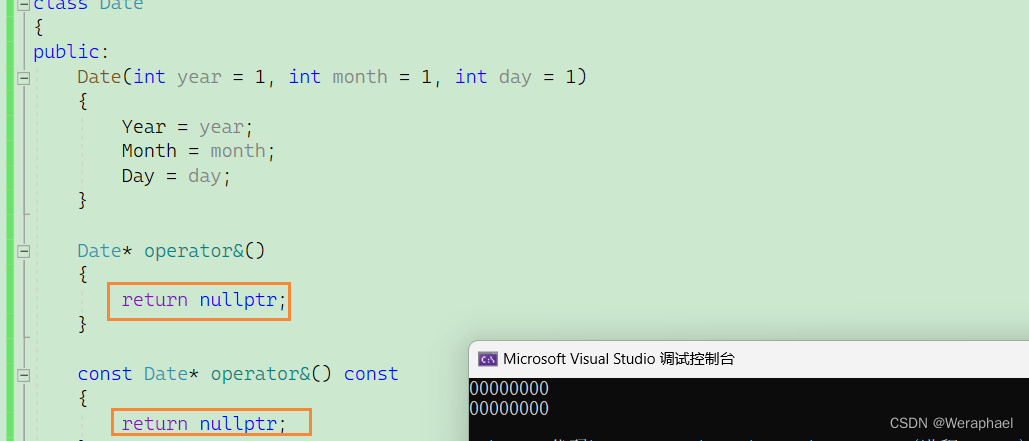
【C++初阶】类与对象(中)之取地址及const取地址操作符重载(了解即可)
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

代驾公司如何管理司机
在这个几乎人人都能学车,人人都能开车的时代,代驾职业也越来越专业化和正规化。因此,想要成为一名优秀的代驾司机,一定得有过人之处,对于代驾公司来说,如何管理司机也是尤为的重要。 对于代驾公司来说&…...
面了一个5年经验的测试工程师,自动化都不会也敢喊了16k,我也是醉了····
在深圳这家金融公司也待了几年,被别人面试过也面试过别人,大大小小的事情也见识不少,今天又是团面的一天, 一百多个人都聚集在一起,因为公司最近在谈项目出来面试就2个人,无奈又被叫到面试房间。 整个过程…...

ChatGPT:你真的了解网络安全吗?浅谈攻击防御进行时之网络安全新定义
ChatGPT:你真的了解网络安全吗?浅谈网络安全攻击防御进行时 网络安全新定义总结 ChatGPT(全名:Chat Generative Pre-trained Transformer),美国OpenAI 研发的聊天机器人程序,是人工智能技术驱动…...
LeetCode_DFS_困难_1377.T 秒后青蛙的位置
目录 1.题目2.思路3.代码实现(Java) 1.题目 给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下: 在一秒内,青蛙从它所在的当前顶点跳到另一个未访问过的顶点(如果它…...
第四十九天学习记录:C语言进阶:结构体
结构体 结构体的声明 结构是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量 struct tag {member-list; }variable-list;问:C的new和C语言的结构体有什么异同? ChatAI答: C中的new是一个运算符ÿ…...

LeeCode [N字形变换]算法解析
关键字:数学归纳法 一、题目 将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下: P A H N A P L S I I G Y I R …...

CPU性能提升:流水线
一条指令的执行一般要经过取指令,翻译指令,执行指令3个基本流程。CPU内部的电路分为不同的单元,取指但愿,译码单元,执行单元等。指令的执行也是按照流水线工序一步步执行的。如图2-34所示,我们假设每一个步…...

C语言指针初级
目录 一、什么是指针 二、指针和指针类型 三、野指针 1.野指针的成因: 2.如何规避野指针 四、指针运算 1.指针-整数 2. 指针之间的加减 五、二级指针 六、指针数组 一个男人,到底要走多少的路,才能成为一个真正的男人 本专栏适用于…...

C++的历史
C是一种广泛使用的编程语言。C于1983年由丹尼斯里奇(Dennis Ritchie)在贝尔实验室创造,它是C语言的扩展。C的设计初衷是为了提高代码的可重用性和可维护性。它允许开发人员使用面向对象编程(OOP)范例,这使得…...
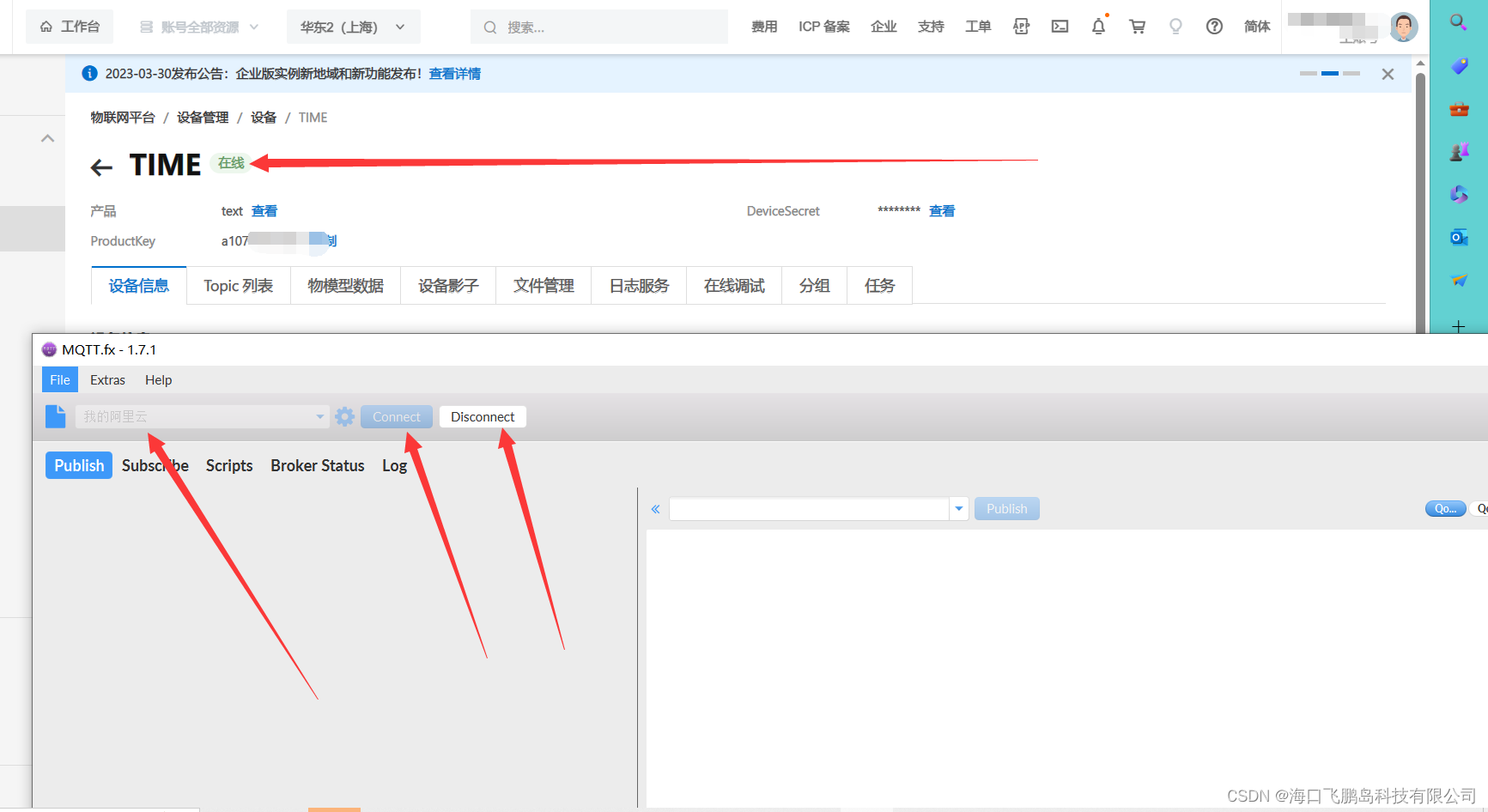
保姆级别!!!--全网绝对教你会!!教你如何使用MQTTFX连接阿里云平台中的设备----下期告诉你如何创建!
本期需要下载的软件 MQttfx安装包,本人打包的-嵌入式文档类资源-CSDN文库 目录 第一步:建造阿里云设备 这个可以先忽略建造步骤,下期将提供步骤。 第二步:下载mqttfx软件 第三步:填写密钥信息进行连接 查看三元…...

Unexpected token ‘‘‘, “‘{“type“:““... is not valid JSON
尝试低代码schema解析JSON时报错,奇怪的是控制台解析正常,项目js执行JSON.parse()报错,简直无语了,,, 只能挨个检查了,首先温习了下JSON 的标准格式: JSON的合法符号:{(左大括号) }(右大括号) "(双引号) :(冒号) ,(逗号) [(左中括号) ](右中括号) JSON字符串:…...

关于C语言的杂记5
文章目录 引入正文内部函数与外部函数相关数组的知识点数组的初始化测试一维数组在内存中存储的地址:遍历二维数组的值测试二维数组的地址(观察内存情况)数组下标为0开始的由来 两个数交换位置的三种方法 引入 写在前面:关于C语言这部分内容,…...

YOLOv5 vs YOLOv6 vs YOLOv7目标检测模型速度和准确度的性能比较——深入研究
如果您正在进行目标检测项目,您很可能会选择众多 YOLO 模型中的一种。从现有的 YOLO 对象检测模型的数量来看,如何选择最佳模型是一个艰难的选择。 您可能会发现自己正在考虑: 选择哪种 YOLO 模型以获得最佳 FPS? CPU 与 GPU 的推理速度如何?选择哪种 GPU?微型、小型、…...

如何增加网站权重?有效提高网站权重的技巧方法
权重对于网站优化来说非常的重要,那什么是网站权重呢?网站权重是指搜索引擎给网站(包括网页)赋予一定的权威值,对网站(含网页)权威的评估评价。一个网站权重越高,在搜索引擎所占的份…...
)
路径规划 | 图解快速随机扩展树RRT算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是RRT算法?2 图解RRT算法原理3 算法仿真与实现3.1 ROS C++实现3.2 Python实现3.3 Matlab实现0 专栏介绍 🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);…...
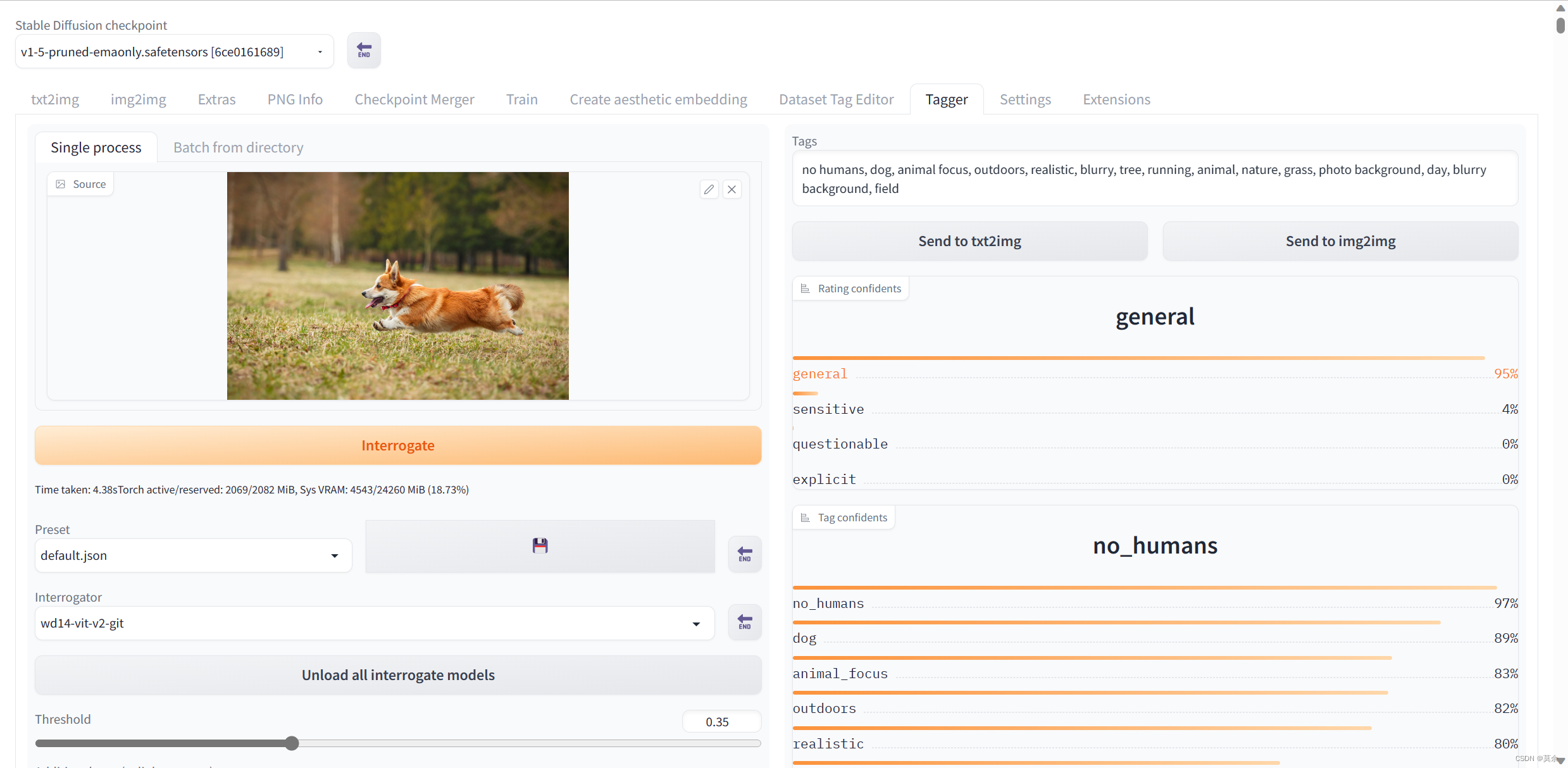
【Stable Diffusion WebUI】一篇文章教你如何安装和使用Stable Diffusion WebUI
文章目录 Stable Diffusion WebUI1. 安装1.1 下载 stable-diffusion-webui1.2 运行 webui.sh 2. 安装插件2.1 命令行安装2.2 extensions 安装2.3 常用插件 3. 使用教程3.1 页面布局3.3 快捷栏设置3.3.1 PNG Info3.3.2 Tagger Stable Diffusion WebUI 1. 安装 1.1 下载 stable…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
