【排序算法】快速排序(Quick Sort)
快速排序(Quick Sort)使用分治法算法思想。
快速排序介绍
它的基本思想是: 选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序实现
从数列中挑出一个基准值。
将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面(相同的数可以到任一边);在这个分区退出之后,该基准就处于数列的中间位置。
递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。
下面以数列a={30,40,60,10,20,50}为例,演示它的快速排序过程(如下图)。
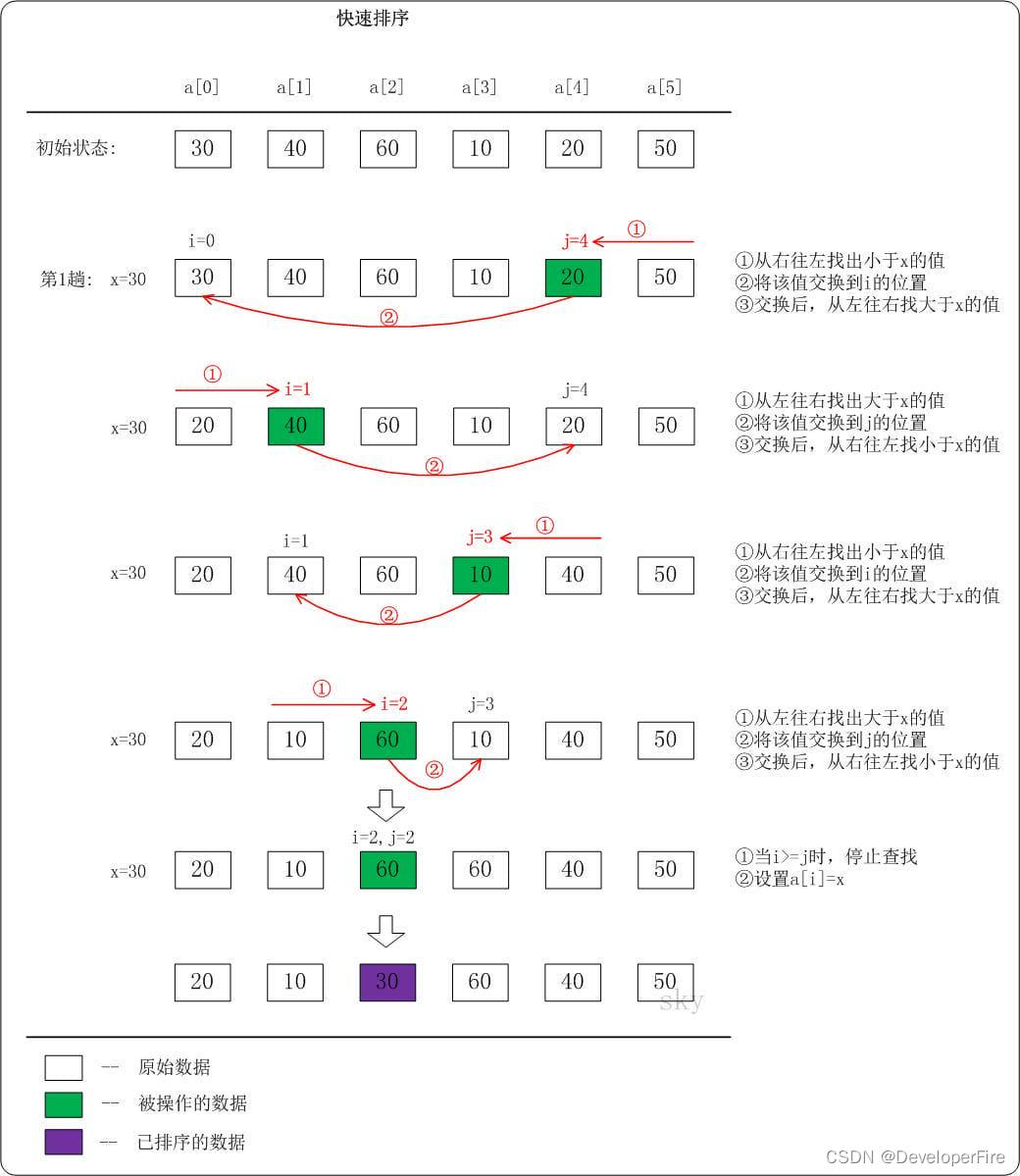
上图只是给出了第1趟快速排序的流程。在第1趟中,设置x=a[i],即x=30。
从"右 --> 左"查找小于x的数: 找到满足条件的数a[j]=20,此时j=4;然后将a[j]赋值a[i],此时i=0;接着从左往右遍历。
从"左 --> 右"查找大于x的数: 找到满足条件的数a[i]=40,此时i=1;然后将a[i]赋值a[j],此时j=4;接着从右往左遍历。
从"右 --> 左"查找小于x的数: 找到满足条件的数a[j]=10,此时j=3;然后将a[j]赋值a[i],此时i=1;接着从左往右遍历。
从"左 --> 右"查找大于x的数: 找到满足条件的数a[i]=60,此时i=2;然后将a[i]赋值a[j],此时j=3;接着从右往左遍历。
从"右 --> 左"查找小于x的数: 没有找到满足条件的数。当i>=j时,停止查找;然后将x赋值给a[i]。此趟遍历结束!
按照同样的方法,对子数列进行递归遍历。最后得到有序数组!
快速排序时间复杂度和稳定性
快速排序稳定性
快速排序是不稳定的算法,它不满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
快速排序时间复杂度
快速排序的时间复杂度在最坏情况下是O(N2),平均的时间复杂度是O(N*lgN)。
这句话很好理解: 假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N),需要遍历多少次呢? 至少lg(N+1)次,最多N次。
为什么最少是lg(N+1)次? 快速排序是采用的分治法进行遍历的,我们将它看作一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的定义,它的深度至少是lg(N+1)。因此,快速排序的遍历次数最少是lg(N+1)次。
为什么最多是N次? 这个应该非常简单,还是将快速排序看作一棵二叉树,它的深度最大是N。因此,快读排序的遍历次数最多是N次。
代码实现
/*** 快速排序: Java** @author skywang* @date 2014/03/11*/public class QuickSort {/** 快速排序** 参数说明: * a -- 待排序的数组* l -- 数组的左边界(例如,从起始位置开始排序,则l=0)* r -- 数组的右边界(例如,排序截至到数组末尾,则r=a.length-1)*/public static void quickSort(int[] a, int l, int r) {if (l < r) {int i,j,x;i = l;j = r;x = a[i];while (i < j) {while(i < j && a[j] > x)j--; // 从右向左找第一个小于x的数if(i < j)a[i++] = a[j];while(i < j && a[i] < x)i++; // 从左向右找第一个大于x的数if(i < j)a[j--] = a[i];}a[i] = x;quickSort(a, l, i-1); /* 递归调用 */quickSort(a, i+1, r); /* 递归调用 */}}public static void main(String[] args) {int i;int a[] = {30,40,60,10,20,50};System.out.printf("before sort:");for (i=0; i<a.length; i++)System.out.printf("%d ", a[i]);System.out.printf("\n");quickSort(a, 0, a.length-1);System.out.printf("after sort:");for (i=0; i<a.length; i++)System.out.printf("%d ", a[i]);System.out.printf("\n");}
}相关文章:

【排序算法】快速排序(Quick Sort)
快速排序(Quick Sort)使用分治法算法思想。快速排序介绍它的基本思想是: 选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排…...
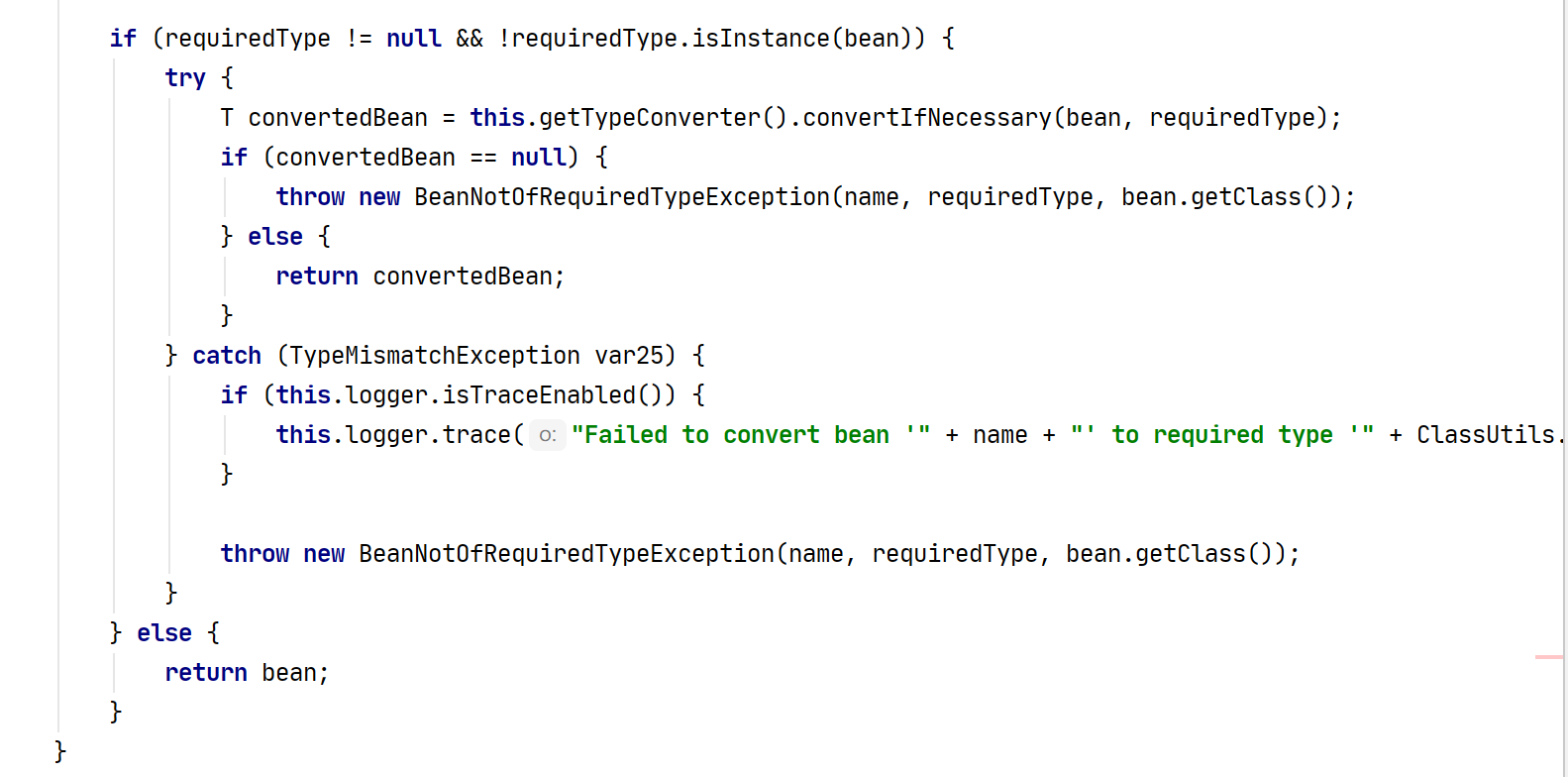
SpringIOC之创建Bean的核心方法doGetBean
概述面向资源(XML、Properties)、面向注解定义的 Bean 是如何被解析成 BeanDefinition(Bean 的“前身”),并保存至 BeanDefinitionRegistry 注册中心里面,实际也是通过 ConcurrentHashMap 进行保存。Spring…...

docker快速部署xxjob2.3.0-SpringBoot快速集成示例
xxjob 2.3.0 部署 参考资料 docker安装xxl-job-admin步骤_JEECG低代码平台的技术博客_51CTO博客 run前准备 1 新建数据库 xxl_job 2 建表sql(可以直接使) https://github.com/xuxueli/xxl-job/blob/master/doc/db/tables_xxl_job.sql建库sql # # XXL-JOB v2.4.0-SNAPSHOT…...
项目管理的前路,前辈能给一些意见吗?
什么是项目管理?关于项目管理的解释主要是基于国际项目管理三大体系不同的解释及本领域权威专家的解释!!!! 项目管理就是以项目为对象的系统管理方法,通过一个临时性的、专门的柔性组织,对项目进行高效率的计划、组织、指导和控制,…...

省钱的年轻人,钱包被折扣店钻了空子
【潮汐商业评论/原创】过年期间,除了商场超市,小区附近的折扣店成了Amy经常光顾的对象。用Amy的话来说,“跟附近超市比价格,跟大卖场比距离,综合下来折扣店就是我随时购物的不二选择。”从Amy的话里,我们可…...

【华为OD机试真题 js、python】优选核酸检测点、寻找核酸检测点【2022 Q4 100分】
代码请进行一定修改后使用,提供有js、python两种语言 题目描述 张三要去外地出差,需要做核酸,需要在指定时间点前做完核酸,请帮他找到满足条件的 核酸检测只点。 给出一组核酸检测点的距离和每个核酸检测点当前的人数给出张三要去做核酸的出发时间 出发时间是10分钟的倍数…...
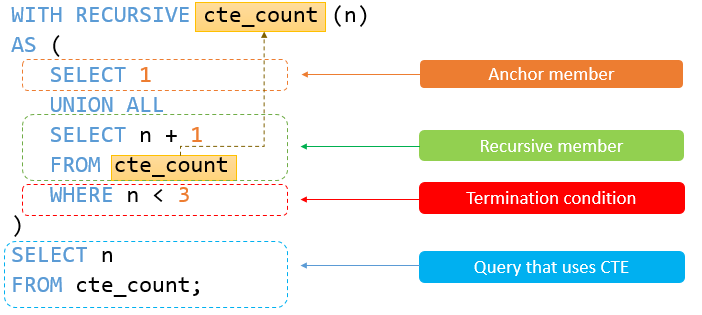
【MySQL】MySQL 8.0 新特性之 - 公用表表达式(CTE)
MySQL 8.0 新特性之 - 公用表表达式(CTE)1. 公用表表达式(CTE) - WITH 介绍1.1 公用表表表达式1.1.1 什么是公用表表达式1.1.2 CTE 语法1.1.3 CTE示例1.3 递归 CTE1.3.1 递归 CTE 简介1.3.2 递归成员限制1.3.3 递归 CTE 示例1.3.4…...

基础面试题:C++中如何理解const修饰符
面试题目:1、题 int i10; const int*p &i; int *const* p &i; const在不同位置有什么不 同 2、const 修饰类成员变量是有什么特殊要求 3、const 修饰类成员函数会发什么 4、const 对象有什么意义 目录 前言 一、const的意义 二、const使用规则 1.初始化…...
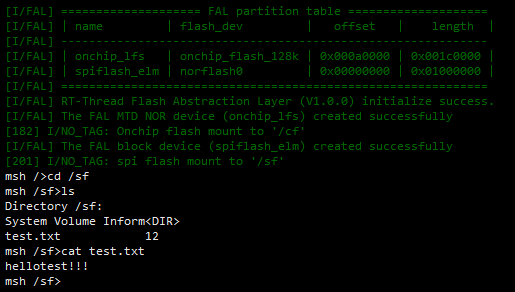
在RT-Thread STM32F407平台下配置SPI flash为U盘
记录下SPI Flash U盘实现过程中踩过的坑,与您分享。前提条件是,需要先将SPI Flash 配置到elm fal文件系统,并挂载成功。如下图然后开始配置USB1,在CubeMX,选择SUB_OTG_FS2 选择USB Device3,确认USB时钟为48…...

数据存储技术复习(二)未完
module3存储是数据中心内的核心元素。请说明常用的存储选项及其特点。磁盘驱动器:具有很大的存储容量,随机读/写访问闪存驱动器:使用半导体介质,提供高性能,低功耗2.若某磁盘驱动器显示每个磁道有八个扇区&…...

使用 QuTrunk+Amazon Deep Learning AMI(TensorFlow2)构建量子神经网络
量子神经网络是基于量子力学原理的计算神经网络模型。1995年,Subhash Kak 和 Ron Chrisley 独立发表了关于量子神经计算的第一个想法,他们致力于量子思维理论,认为量子效应在认知功能中起作用。然而,量子神经网络的典型研究涉及将…...
python selenium浏览器复用技术
使用selenium 做web自动化的时候,经常会遇到这样一种需求,是否可以在已经打开的浏览器基础上继续运行自动化脚本? 这样前面的验证码登录可以手工点过去,后面页面使用脚本继续执行,这样可以解决很大的一个痛点。 命令行…...

第二章:创建虚拟机
创建Windows server:首先第一步就是打开我们的vm,然后找到上一章讲的主页图标创建新的虚拟机。点击这上面类似的,然后转站。博文地址:https://blog.csdn.net/ryduijftgvhj/article/details/127934939?spm1001.2014.3001.5502视频…...

码上【call,apply,bind】的手写
一、call (1)官方用法 call() 方法使用一个指定的 this 值和单独给出的一个或多个参数来调用一个函数。 语法:function.call(要绑定的this值,参数,参数,…)。不一定这些参数都需要,这些参数都…...
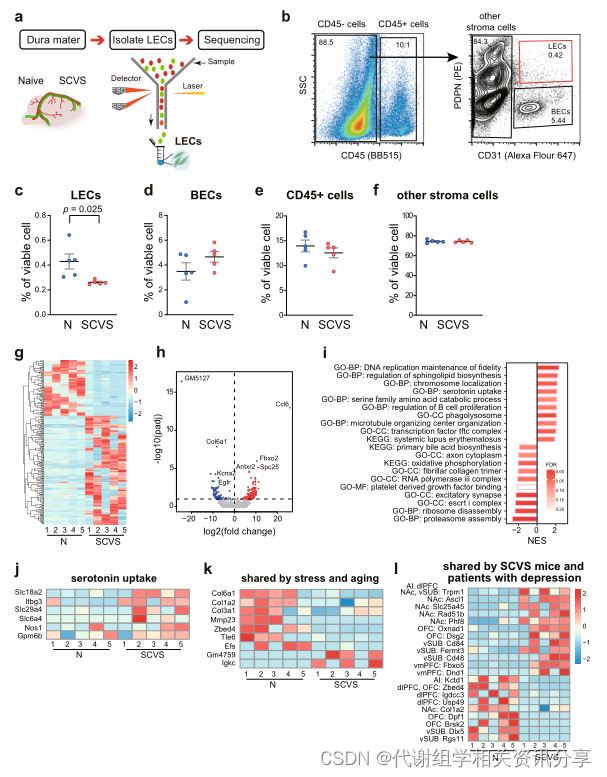
代谢组学Nature子刊!抑郁症居然“男女有别”,脑膜淋巴管起关键作用!
文章标题:A functional role of meningeal lymphatics in sex difference of stress susceptibility in mice 发表期刊:Nature Communications 影响因子:17.694 发表时间:2022年8月 作者单位:中山大学中山医学院 …...
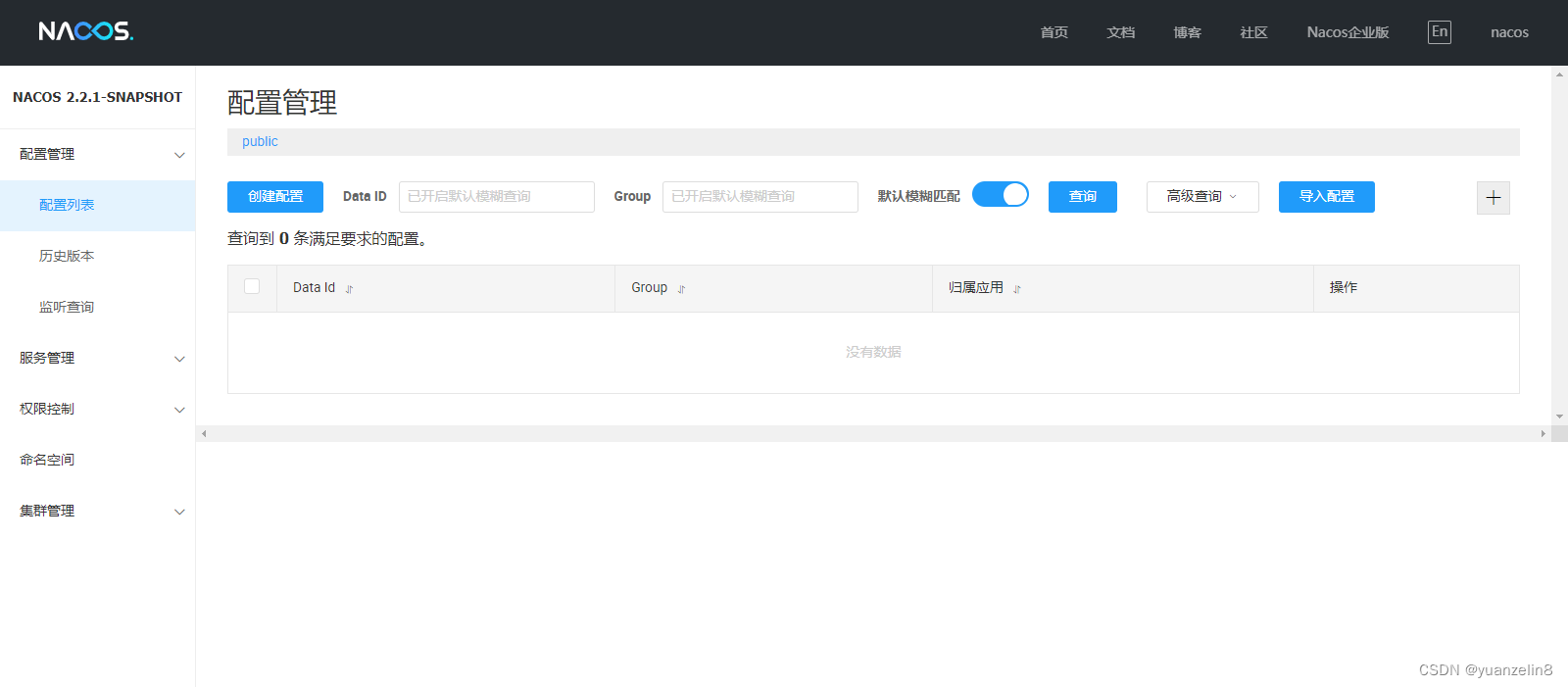
nacos配置中心搭建
网站每次更新版本都有短暂暂停,影响用户使用,返回经常不可用,需要改进 需要实现高可用,搭建负载均衡,实现jenkinsnacos不停机部署 nacos搭建预备环境准备 64 bit OS,支持 Linux/Unix/Mac/Windows&#x…...
uni-app低成本封装一个取色器组件
在uni-ui中找不到对应的工具 后面想想也是 移动端取色干什么? 没办法 也挂不住特殊需求 因为去应用市场下载 这总东西 又不是很有必要 那么 下面这个组件或许能解决您的烦恼 <template><view class"content"><view class"dialog&…...
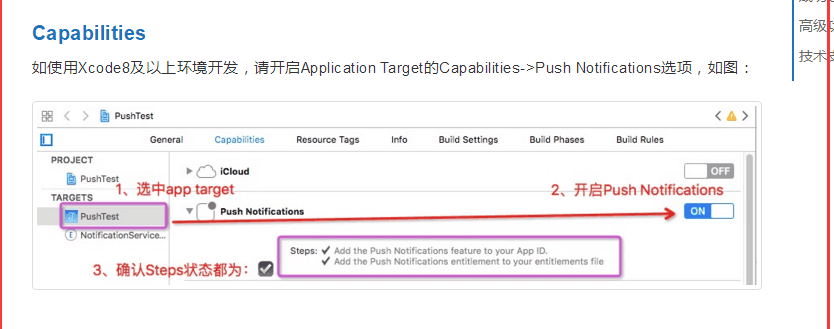
APP 怎么免费接入 MobPush
1、获取 AppKey 申请 Appkey 的流程,请点击 http://bbs.mob.com/thread-8212-1-1.html?fromuid70819 2、下载 SDK 下载解压后,如下图: 目录结构 (1)Sample:演示Demo。(2)SDK&am…...

XGBoost
目录 1.XGBoost推导示意图 2.分裂节点算法 Weighted Quantile Sketch 3.对缺失值得处理 1.XGBoost推导示意图 XGBoost有两个很不错得典型算法,分别是用来进行分裂节点选择和缺失值处理 2.分裂节点算法 Weighted Quantile Sketch 对于特征切点点得选择ÿ…...
你是什么时候从轻视到高看软件测试的?
刚开始学软件测试很轻视,因为我那时很无知,这也是那时绝大多数人员的心态,那时中国最讲究“编程才是硬道理”。 如今却非常热爱软件测试,包括软件测试工具,方法,理论,技术。因为我在3年的测试工…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
