矩阵理论复习(十二)
已知方阵A的不变因子:
- 求谱半径
- 求矩阵级数
- 判断矩阵幂级数的收敛性

若矩阵B的某个算子范数小于1,则I-B可逆。
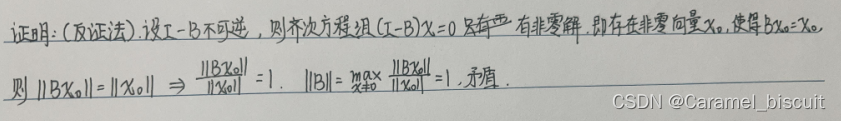


矩阵分析


任何相容矩阵范数都存在与之相容的向量范数。
盖尔圆盘定理一的证明

椭圆范数的证明
若||.||是Cm上的向量范数,A为列满秩矩阵,则||A.||是Cn上的向量范数。

椭圆范数的应用
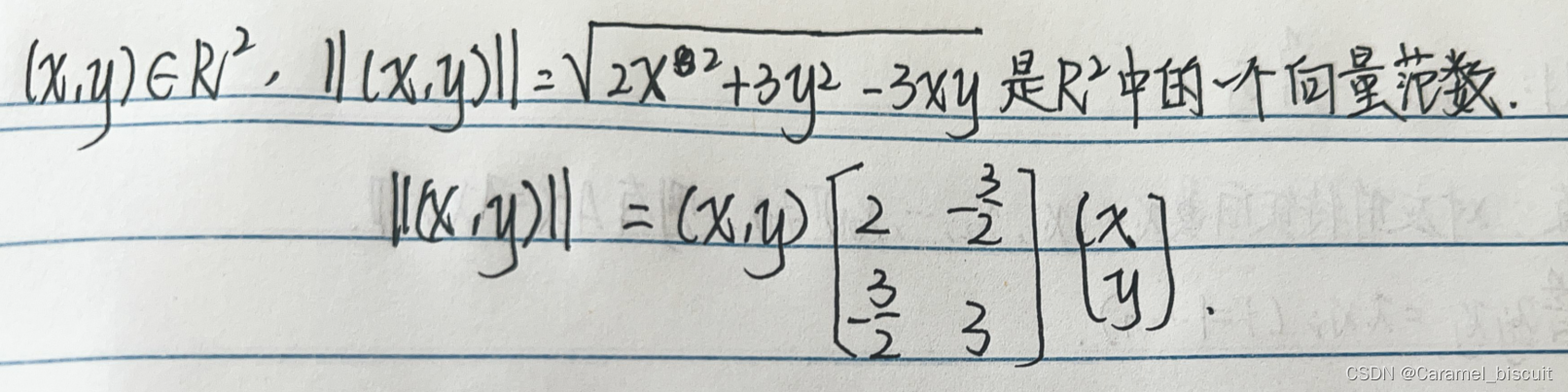
Rayleigh商
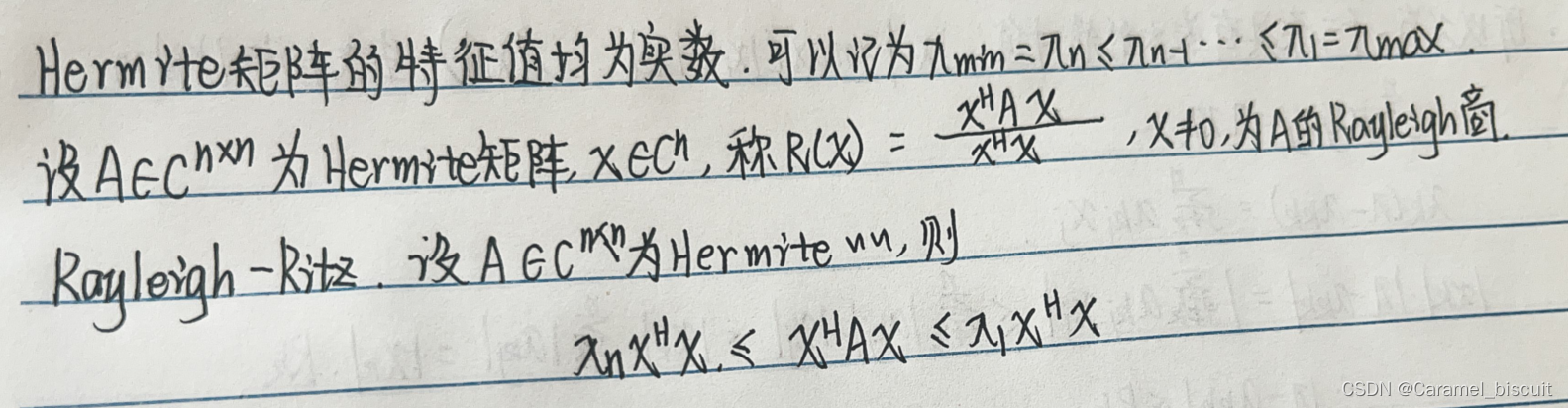
R(A+)=R(AH)
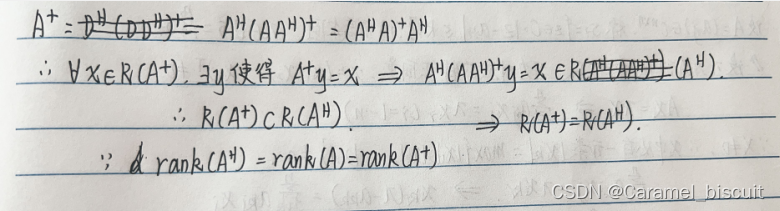
A+=AH(AAH)+=(AHA)+AH
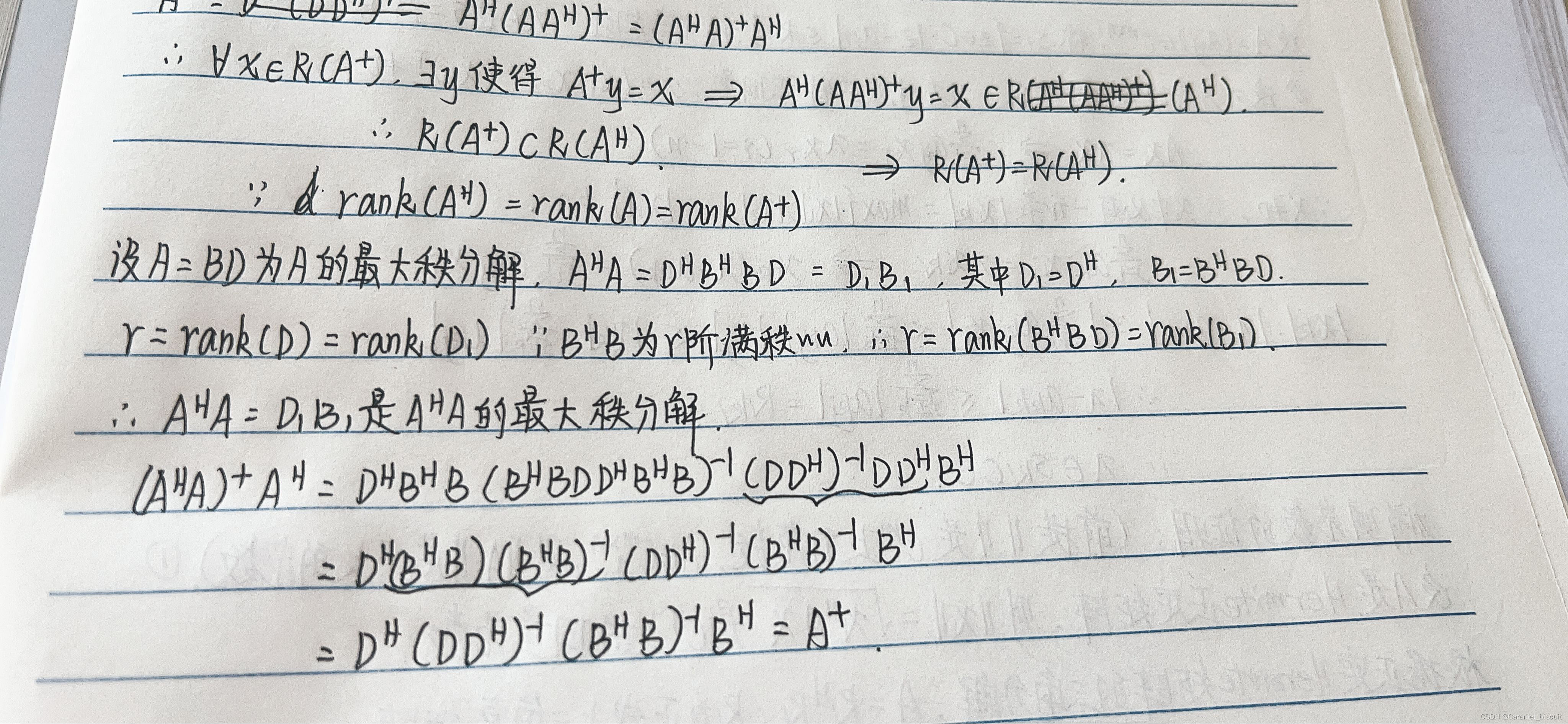
当A的某算子范数小于1时,证明E-A可逆

证明自反广义逆
- AGA=A
- rank(G)=rank(A)
证明G=YZ是A的自反广义逆

B=[A+ A+]

设T是线性空间V上的投影,则投影的值域和核互为直和补。

维数定理

直和
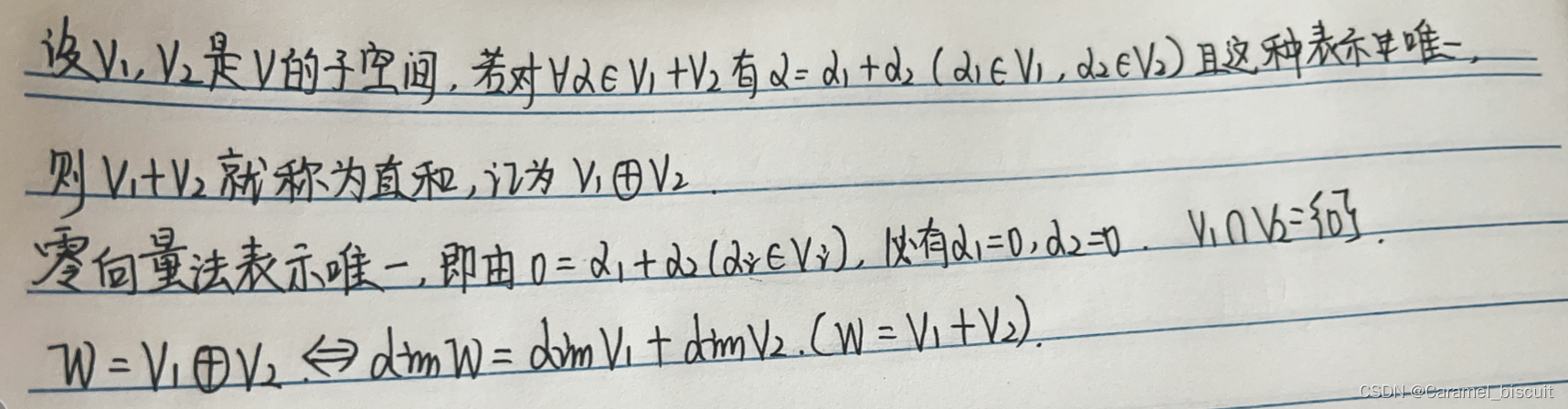
正规矩阵A的特征值的模等于A的奇异值
rank(A)=rank(AH)=rank((AHA)=rank((AAH)

三角矩阵的结论
- 上三角矩阵的逆仍是上三角矩阵,且对角元是R对角元的倒数。
- 两个上三角矩阵的乘积仍是上三角矩阵,且对角元是R1,R2对角元的乘积。
- 酉矩阵的逆还是酉矩阵,酉矩阵的乘积仍是酉矩阵。
相关文章:

矩阵理论复习(十二)
已知方阵A的不变因子: 求谱半径求矩阵级数判断矩阵幂级数的收敛性 若矩阵B的某个算子范数小于1,则I-B可逆。 矩阵分析 任何相容矩阵范数都存在与之相容的向量范数。 盖尔圆盘定理一的证明 椭圆范数的证明 若||.||是Cm上的向量范数,A为…...
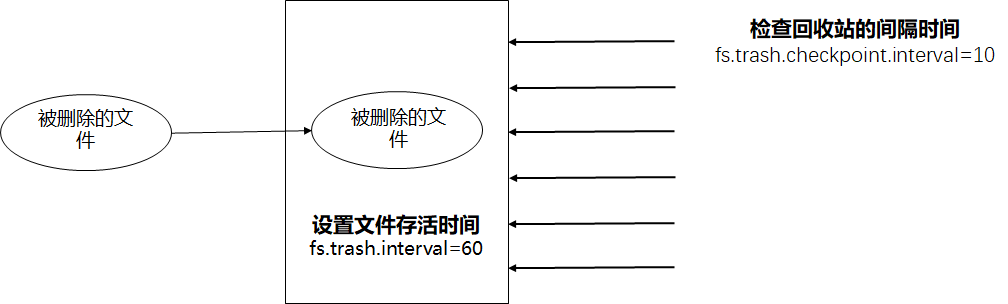
大数据框架之Hadoop:HDFS(七)HDFS 2.X新特性
7.1集群间数据拷贝 scp实现两个远程主机之间的文件复制 scp -r hello.txt roothadoop103:/root/hello.txt // 推 push scp -r roothadoop103:/root/hello.txt hello.txt // 拉 pull scp -r roothadoop103:/root/hello.txt roothadoop104:/root //是通过本地主机中…...
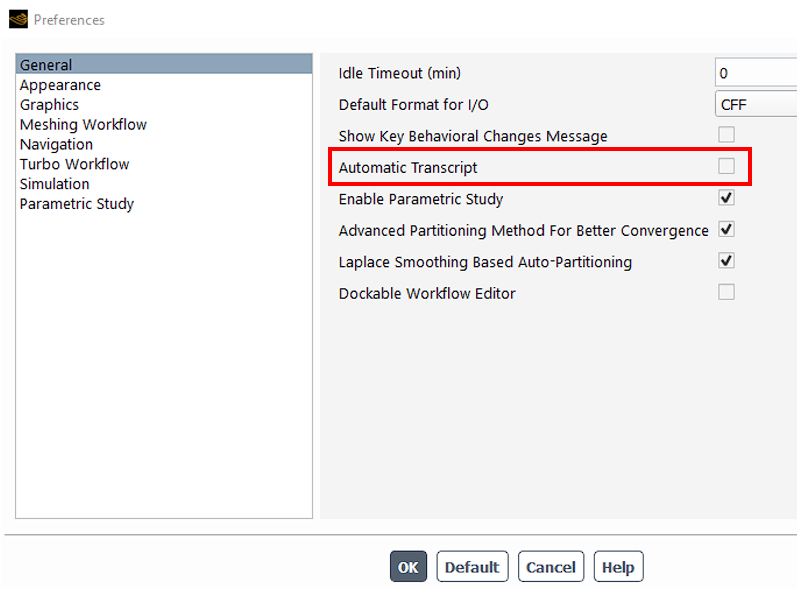
Fluent工作目录
1 工作目录定义工作目录(working directory)是一种文件存储路径设置方式。基于工作目录的方法,写文件时只需要指定文件名,而不需要指定完全的文件路径,从而简化程序编写,对不同操作系统环境有更好的适应性。…...

Learning C++ No.10【STL No.2】
引言: 北京时间:2023/2/14/23:18,放假两个月,没有锻炼,今天去跑了几圈,一个字,累,感觉人都要原地升天了,所以各位小伙伴,准确的说是各位卷王,一定…...
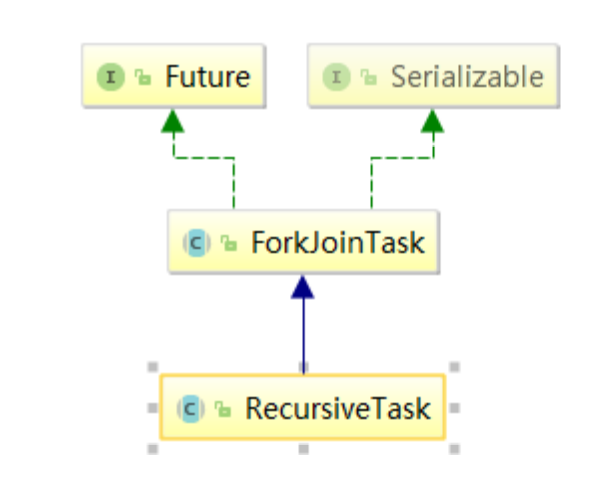
【java 高并发编程之JUC】2w字带你JUC从入门到精通
点击查看脑图目录地址,实时更新 1 什么是 JUC 1.1 JUC 简介 在 Java 中,线程部分是一个重点,本篇文章说的 JUC 也是关于线程的。JUC 就是 java.util .concurrent 工具包的简称。这是一个处理线程的工具包,JDK 1.5 开始出现的。 1.2 进程与…...
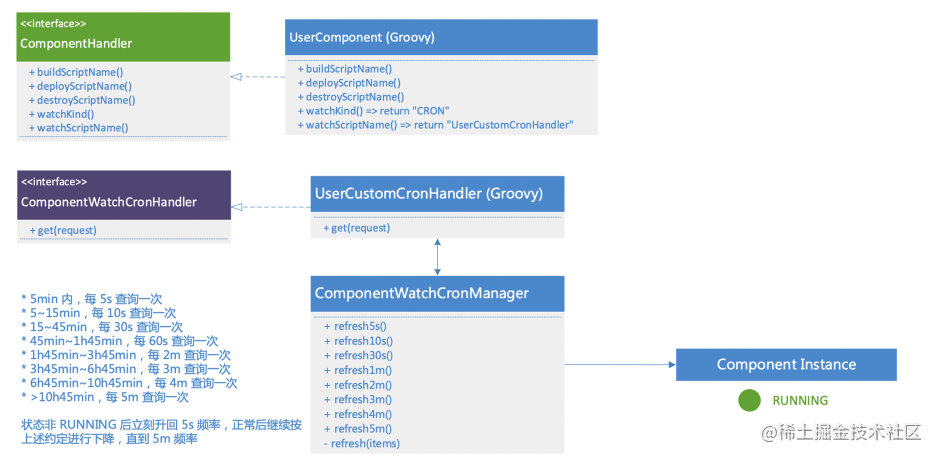
QCon演讲实录(下):多云管理关键能力实现与解析-AppManager
在上篇中,我们已经基本了解了多云管理。现在,我们将深入探讨多云管理关键能力实现:AppManager。 什么是AppManager? 上面我们讲了理论、我们自己使用的交付流程和整体架构,下面我们进入关键能力实现与解析的环节&…...

刚刚退出了一个群,关于在要麒麟OS上运行Labview
年龄过了45,看问题,与以前不太一样了。 觉得浪费时间的事,宁可发呆,也不会参和。 竟然一个群里在讨论如何满足客户的需求:麒麟OS上运行Labview。 然后直接退了群。 这种问题,我觉得可能 发在csdn上&…...

el-uploader 文件上传后,又被修改,无法提交到后端 ERR_UPLOAD_FILE_CHANGED
problem 文件上传后,又被修改,无法提交到后端 具体步骤: 文件上传本地文件打开并修改保存提交ajax 这个问题不仅仅局限于el-uploader,是一个普遍性的问题 导致的问题 问题1:提交请求时,控制台报错 net…...

利用Eigen实现点云体素滤波
目录 前言 一、算法原理 二、代码实现 1.头文件 2.源文件 三、效果展示 前言 体素滤波原理简单,是常用的...

linux高级命令之多进程的使用
多进程的使用学习目标能够使用多进程完成多任务1 导入进程包#导入进程包import multiprocessing2. Process进程类的说明Process([group [, target [, name [, args [, kwargs]]]]])group:指定进程组,目前只能使用Nonetarget:执行的目标任务名…...

CSS 圆角边框 盒子阴影 文字阴影
目录 1.圆角边框(重点) 2.盒子阴影(box-shadow) 3.文字阴影(text-shadow) 1.圆角边框(重点) border-radius 属性用于设置元素的外边框圆角。 语法: border-radius: l…...

python简单解析打印onnx模型信息
当我们加载了一个ONNX之后,我们获得的就是一个ModelProto,它包含了一些版本信息,生产者信息和一个GraphProto。在GraphProto里面又包含了四个repeated数组,它们分别是node(NodeProto类型),input(ValueInfoProto类型)&a…...
UE4 编写着色器以及各种宏的理解
参考链接:如何为 UE4 添加全局着色器(Global Shaders) - Unreal Enginehttps://docs.unrealengine.com/5.1/zh-CN/adding-global-shaders-to-unreal-engine/如何为 UE4 添加全局着色器(Global Shaders) - Unreal Engin…...

小笔记:Python 使用字符串调用函数
小笔记:Python中如何使用字符串调用函数/方法?jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 本文地址:https://blog.csdn.net/qq_28550263/article/details/111874476 邮箱 :291148484163.co…...

红黑树的原理+实现
文章目录红黑树定义性质红黑树的插入动态效果演示代码测试红黑树红黑树 定义 红黑树是一个近似平衡的搜索树,关于近似平衡主要体现在最长路径小于最短路径的两倍(我认为这是红黑树核心原则),为了达到这个原则,红黑树所…...
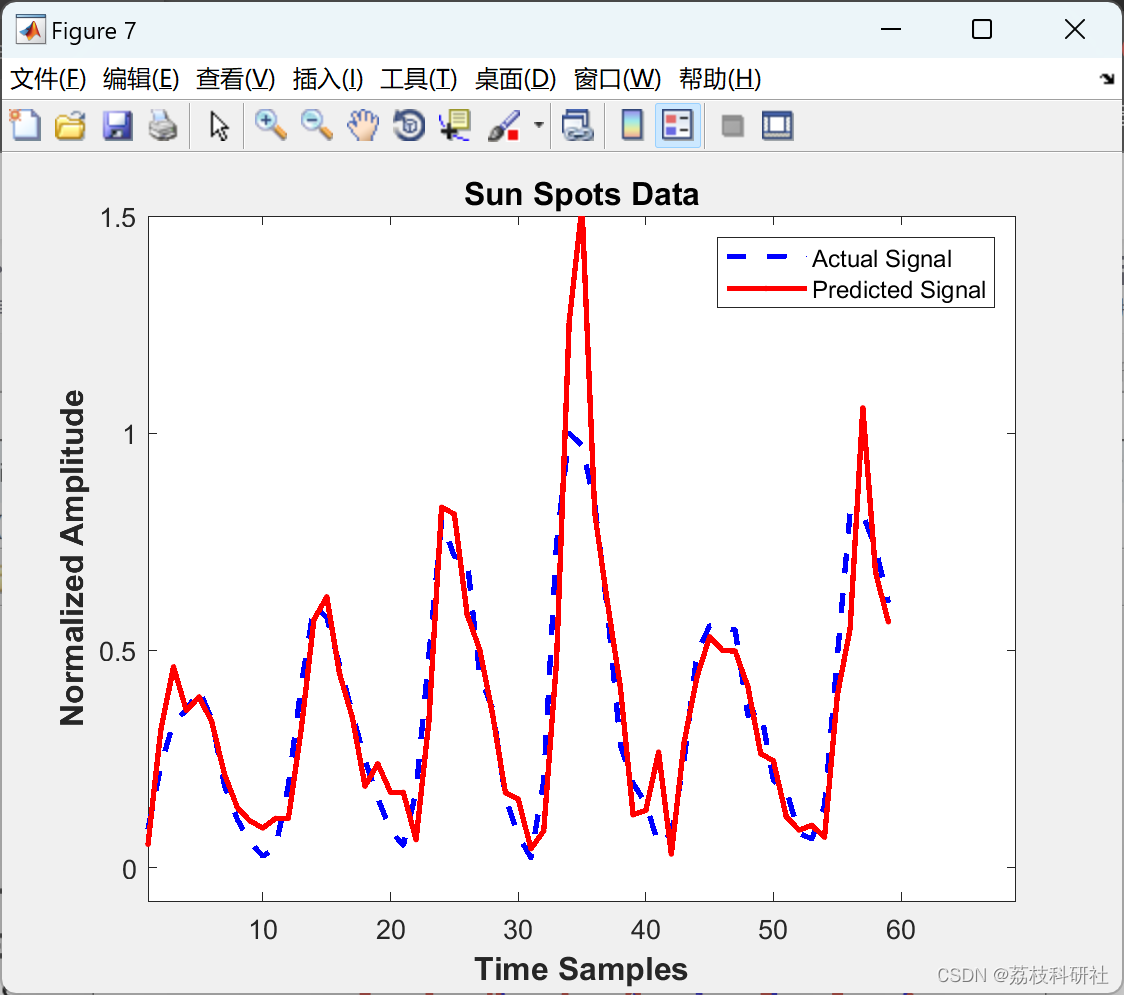
用于非线性时间序列预测的稀疏局部线性和邻域嵌入(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

使用 Vue3 重构 Vue2 项目
目录前言:一、项目整体效果展示二、项目下载使用方法三、为什么要重构项目四、重构的流程五、步骤中的 bug 以及解决方式六、未解决的问题总结:前言: 2020年9月18日,vue3正式版发布了,前几天学习完成后,我决…...
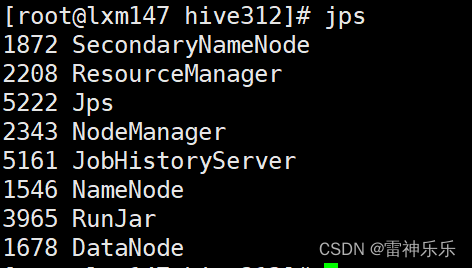
Hive学习——单机版Hive的安装
目录 一、基本概念 (一)什么是Hive (二)优势和特点 (三)Hive元数据管理 二、Hive环境搭建 1.自动安装脚本 2./opt/soft/hive312/conf目录下创建hive配置文件hive-site.xml 3.拷贝一个jar包到hive下面的lib目录下 4.删除hive的guava,拷贝hadoop下的guava 5…...
uprobe 实战
观测数据源 目前按照我的理解,和trace相关的常用数据源–探针 大致分为四类。 内核 Trace point kprobe 用户程序 USDT uprobe 在用户程序中,USDT是所谓的静态Tracepoint。和内核代码中的Trace point类似。实现方式是在代码开发时,使用USDT…...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 求最大数字(Python)| 真题+思路+考点+代码+岗位
求最大数字 题目 给定一个由纯数字组成以字符串表示的数值,现要求字符串中的每个数字最多只能出现2次,超过的需要进行删除;删除某个重复的数字后,其它数字相对位置保持不变。 如34533,数字3重复超过2次,需要删除其中一个3,删除第一个3后获得最大数值4533 请返回经过删…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
