算法Day16 | 104.二叉树的最大深度,559.n叉树的最大深度, 111.二叉树的最小深度,222.完全二叉树的节点个数
Day16
- 104.二叉树的最大深度
- 559.n叉树的最大深度
- 111.二叉树的最小深度
- 222.完全二叉树的节点个数
104.二叉树的最大深度
题目链接: 104.二叉树的最大深度
深度和高度相反。
高度,自然是从下向上数:叶子节点是第一层,往上数,越来越多。用后序遍历来求高度。(自己排一遍后序遍历,注意中间节点的位置,最后再处理根节点)
深度,自然是从上向下数:根节点是第一层,往下数,越来越多。用前序遍历来求深度。
递归:用后序遍历求高度(本题高度相当于深度)
class Solution {
public:int recursion(TreeNode* cur) {if (!cur) return 0;int left = recursion(cur->left);//左 int right = recursion(cur->right);//右//处理成高度,子节点数值 + 1return 1 + max(left, right);//中}int maxDepth(TreeNode* root) {return recursion(root);}
};
递归:用前序遍历求深度
class Solution {
public://每个递归函数中,都有一个resultint result = 0;//递归中用到result,也可以写到函数参数中void recursion(TreeNode* cur, int depth) {result = result > depth ? result : depth;//中。取最大值if (!cur->left && !cur->right) return;if (cur->left) recursion(cur->left, depth + 1);//左if (cur->right) recursion(cur->right, depth + 1);//右}int maxDepth(TreeNode* root) {if (!root) return 0;recursion(root, 1);return result;}
};
迭代法 层序遍历。
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;if (root) que.push(root);int res = 0;while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}++res;}return res;}
};559.n叉树的最大深度
题目链接:559.n叉树的最大深度
递归 后序遍历。
class Solution {
public:int maxDepth(Node* root) {if (!root) return 0;int depth = 0;for (auto& i: root->children) {depth = max(depth, maxDepth(i));//子节点中最高}return depth + 1;}
};
层序迭代
class Solution {
public:int maxDepth(Node* root) {queue<Node*> que;if(!root) return 0;else que.push(root);int depth = 0;while (!que.empty()) {int size = que.size();while (size--) {Node* cur = que.front();que.pop();for (auto& i : cur->children) {que.push(i);}}++depth;}return depth;}
};
111.二叉树的最小深度
题目链接: 111.二叉树的最小深度
递归 后序遍历
class Solution {
public:int minDepth(TreeNode* root) {if (!root) return 0;int left = minDepth(root->left);//左int right = minDepth(root->right);//右//中if (!root->left && root->right)return 1 + right;if (root->left && !root->right)return 1 + left;return 1 + min(left, right);}
};
递归前序遍历
class Solution {
public:int res = INT_MAX;void recursion(TreeNode* cur, int depth) {if (!cur) return;//中if (!cur->left && !cur->right) {res = min(res, depth);}if (cur->left) recursion(cur->left, depth + 1);//左if (cur->right) recursion(cur->right, depth + 1);//右return;}int minDepth(TreeNode* root) {if (!root) return 0;recursion(root, 1);return res;}
};
迭代 层序遍历
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> que;if (!root) return 0;if (root) que.push(root);int res = 1;//至少有一层while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);if (!cur->left && !cur->right) return res;}++res;}return res;}
};
222.完全二叉树的节点个数
题目链接:222.完全二叉树的节点个数
通过完全二叉树的性质,判断子树是否为满二叉树,通过 2 k − 1 2^k-1 2k−1来加速计算节点个数。
递归 后序遍历
class Solution {
public:int countNodes(TreeNode* root) {if (!root) return 0;//判断是否为满二叉树TreeNode* l = root->left, * r = root->right;int leftCnt = 0, rightCnt = 0;while (l) {l = l->left;++leftCnt;}while (r) {r = r->right;++rightCnt;}if (leftCnt == rightCnt) return (2 << leftCnt) - 1;//注意<<的优先级小于-的优先级int leftSum = countNodes(root->left);//左int rightSum = countNodes(root->right);//右return leftSum + rightSum + 1/*cur节点*/;//中}
};
迭代层序遍历
class Solution {
public:int countNodes(TreeNode* root) {queue<TreeNode*> que;if (!root) return 0;else que.push(root);int cnt = 0;while (!que.empty()) {int size = que.size();while (size--) {TreeNode* cur = que.front();que.pop();++cnt;if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return cnt;}
};
相关文章:

算法Day16 | 104.二叉树的最大深度,559.n叉树的最大深度, 111.二叉树的最小深度,222.完全二叉树的节点个数
Day16 104.二叉树的最大深度559.n叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数 104.二叉树的最大深度 题目链接: 104.二叉树的最大深度 深度和高度相反。 高度,自然是从下向上数:叶子节点是第一层,往上数&#x…...

java设计模式之责任链设计模式的前世今生
责任链设计模式是什么? 责任链设计模式(Chain of Responsibility Pattern)是一种行为型设计模式,它允许多个对象都有机会处理请求,从而避免请求的发送者与接收者之间的耦合关系。在责任链模式中,每个处理对…...

是面试官放水,还是公司太缺人了?华为原来这么容易就进了...
华为是大企业,是不是很难进去啊?” “在华为做软件测试,能得到很好的发展吗? 一进去就有9.5K,其实也没有想的那么难” 直到现在,心情都还是无比激动! 本人211非科班,之前在字节和腾…...
PLC/DCS系统常见的干扰现象及判断方法
一般来说,常见的干扰现象有以下几种: 1.系统发指令时,电机无规则地转动; 2.信号等于零时,数字显示表数值乱跳; 3。传感器工作时,DCS/PLC 采集过来的信号与实际参数所对应的信号值不吻合,且误…...
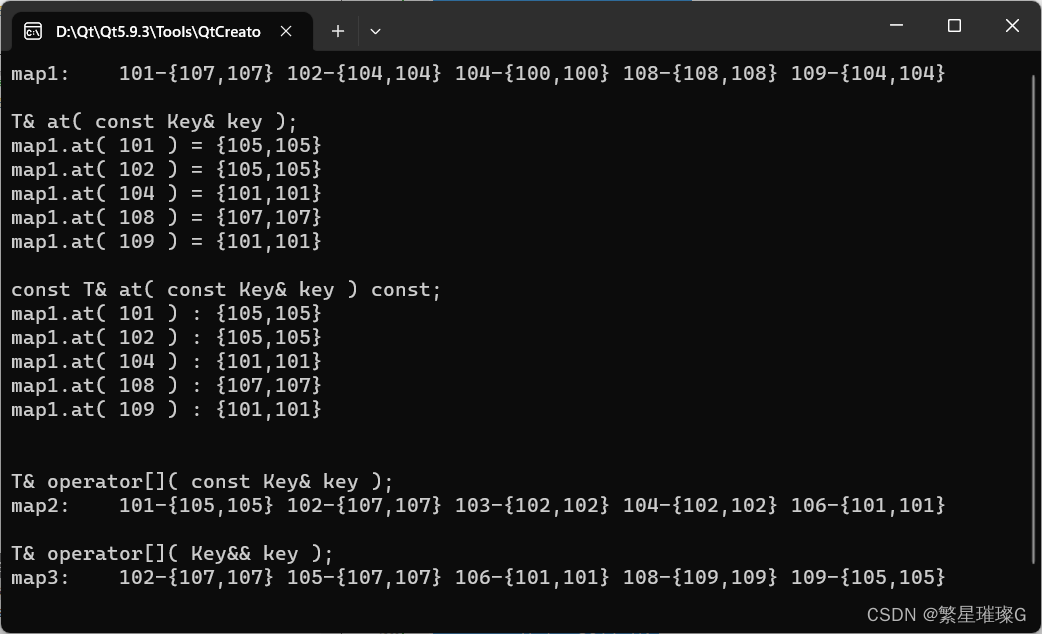
c++ 11标准模板(STL) std::map(四)
定义于头文件<map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class map;(1)namespace pmr { template <class Key, class T, clas…...

6.开源非对称加密算法SM2实现
6.开源非对称加密算法SM2实现 前期内容导读: 开源加解密RSA/AES/SHA1/PGP/SM2/SM3/SM4介绍开源AES/SM4/3DES对称加密算法介绍及其实现开源AES/SM4/3DES对称加密算法的验证实现开源非对称加密算法RSA/SM2实现及其应用开源非对称加密算法RSA实现 1. 开源组件 非对称秘…...
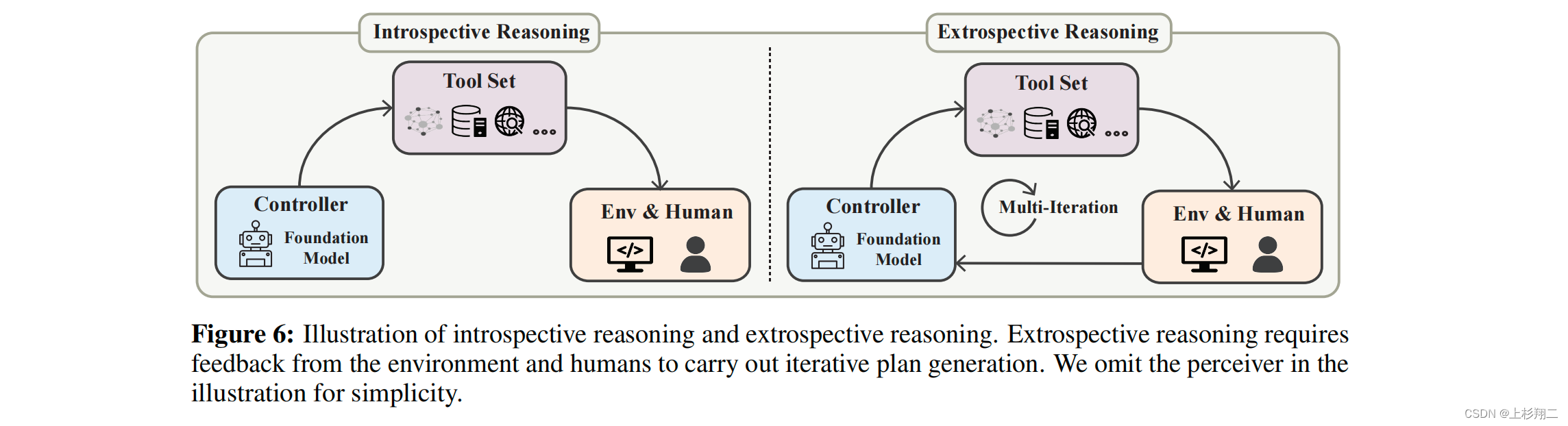
Toolformer and Tool Learning(LLMs如何使用工具)
大模型的能力让学术和工业界都对通用人工智能的未来充满幻想,在前一篇博文中已经粗略介绍, Augmented Language Models(增强语言模型) ALM的两大思路是推理和工具,本篇博文整理两篇关于Toolformer或Tool Learning的论…...

029:Mapbox GL绘制铁路黑白交替的线段
第029个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中加载数据显示铁路标识的那种黑白交替的线段。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共94行)相关API参考:专栏目标示例效果 配置方式 1)…...

结对编程 --- 大部分程序员喜欢的编程方式
一、介绍 结对编程起源时间可以追溯到 1990 年代早期。这种编程方法最初由 Jim Highsmith 和 Alistair Cockburn 等人提出。后来,Kent Beck 和 Ward Cunningham 等人将其发展成为一种敏捷开发方法,被称为“极限编程”(Extreme Programming&am…...
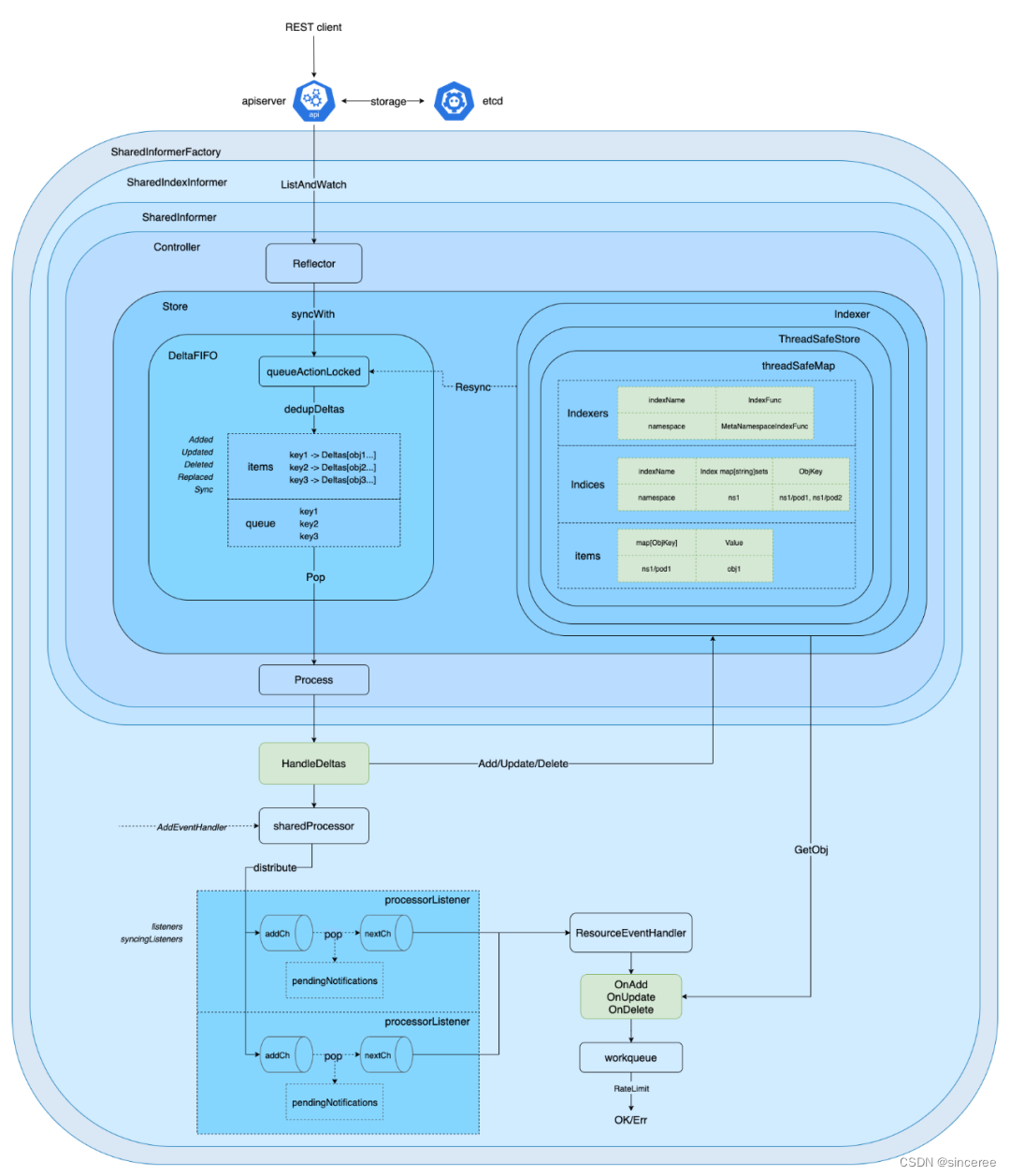
kubernetes-informer机制
一、概念 informer 是 client-go 中的核心工具包,在kubernetes中,各个组件通过HTTP协议跟 API Server 进行通信。如果各组件每次都直接和API Server 进行交互,会给API Server 和ETCD造成非常大的压力。在不依赖任何中间件的情况下࿰…...

LeetCode 2451. Odd String Difference【字符串,哈希表】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
切片工具tippecanoe的全网最详细的解释
1.下载和安装 tippecanoe工具是mapbox官方提供的一个服务端切片工具,因此它是运行在服务器上的,它比较友好的支持mac和linux机器。对于windows来讲,就比较麻烦了。 首先对于mac系统,你只需配置好自己的homebrew,保证homebrew能够正常下载东西。 然后只需要一个命令: …...
Linux系统初始化命令的备忘单,Linux运维工程师收藏!
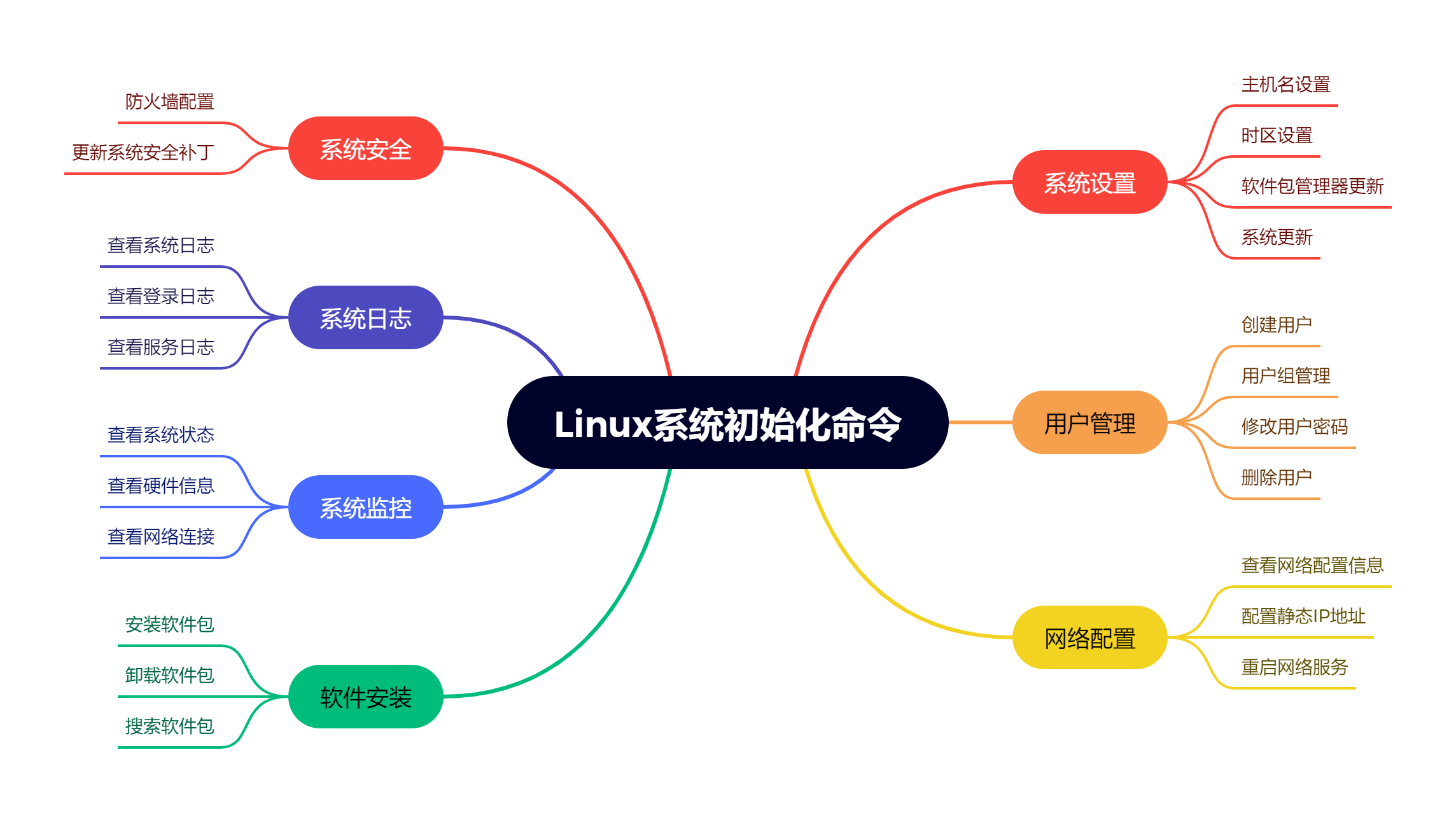
在管理和维护Linux系统时,有一些常用的命令可以帮助您进行系统初始化和配置。这些命令涵盖了各种任务,包括系统设置、用户管理、软件安装和网络配置等。 本文将为您提供一个Linux系统初始化命令的备忘单,以便在需要时方便查阅和使用。 系统设…...

五月最近一次面试,被阿里P8测开虐惨了...
都说金三银四涨薪季,我是着急忙慌的准备简历——5年软件测试经验,可独立测试大型产品项目,熟悉项目测试流程...薪资要求?5年测试经验起码能要个20K吧 我加班肝了一页半简历,投出去一周,面试电话倒是不少&a…...
工业机器视觉缺陷检测工作小结
工业机器视觉检测工作小结 (因为网上没有很系统的讲义和文档,都是零零散散的,因此,我自己尝试着总结一下、仅供参考) 你想知道的大概率在这都可以找到、相机的了解镜头的了解光源的了解传统算法DL深度学习方法 &#…...

技术笔记:默默耕耘,赢得铁粉的秘密策略!
目录 第一步:真实实践,价值分享第二步:高质量文章的撰写第三步:积极互动,回复评论和留言第四步:定期更新和持续学习第五步:参与技术社区第六步:社区问答和问题解答总结 导语…...
回收站中怎么找回误删除的文件?这几种方法很实用
当我们在电脑上操作文件的时候,难免会有不小心删除文件的情况发生。这个时候,我们可以打开回收站来找回误删除的文件。但是,有时候我们也会误将回收站清空。那么,该怎样才能找回已经误删除的文件呢?在这里提供了回收站…...
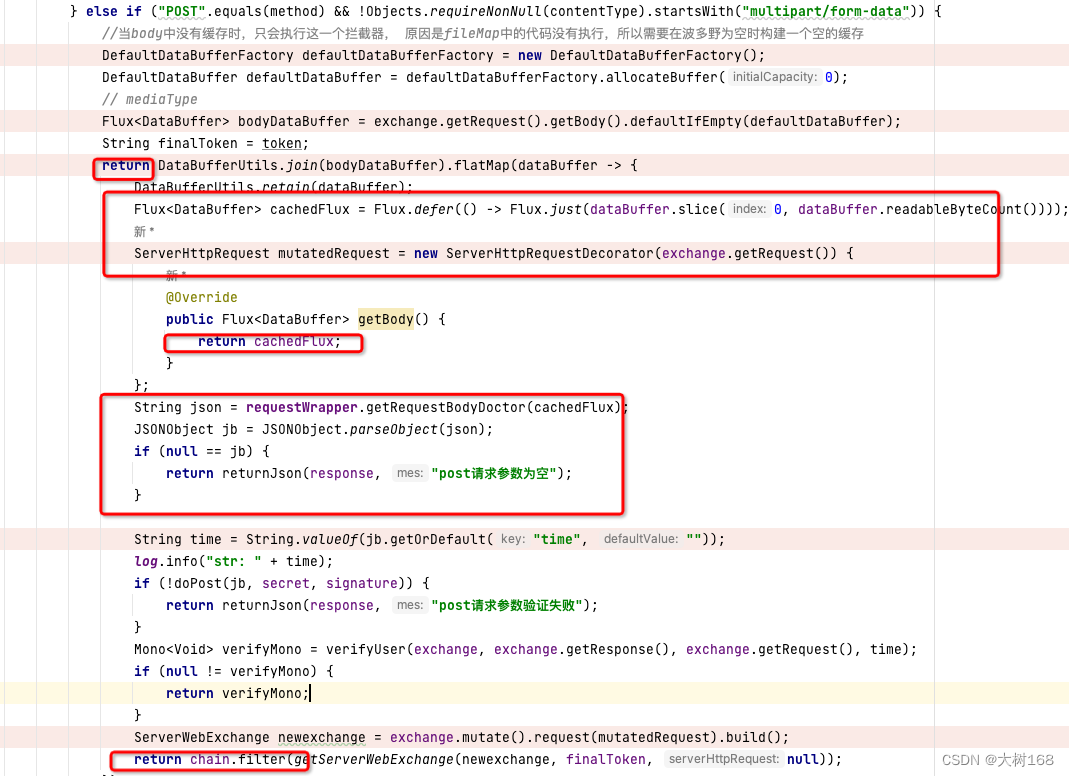
Gateway网关参数进行验签POST 包含requestbody 请求体封装
Gateway网关自定义拦截器的不可重复读取数据 特别注意一点, 因为在网关层 拿出 request 流之后,必须重写getbody()方法把所有的参数放进去,否则后面转发的请求无法接收到任何数据, 坑,巨坑,因为版本问题网上很多都不能兼容, 我的springboot环境 依赖包 <parent><gr…...
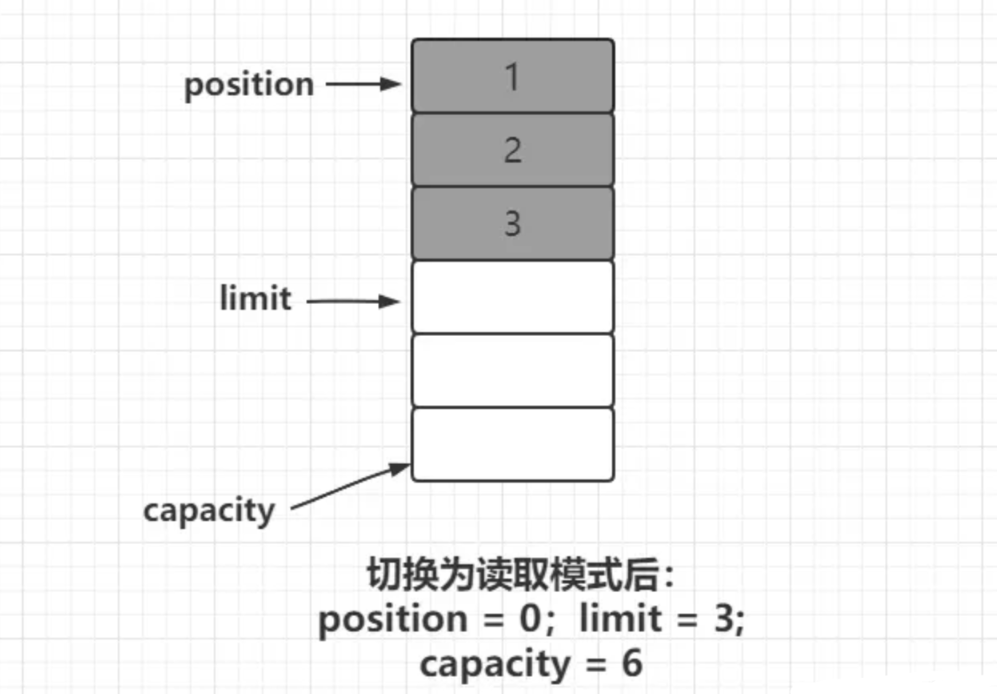
【Netty】字节缓冲区 ByteBuf (六)(上)
文章目录 前言一、ByteBuf类二、ByteBuffer 实现原理2.1 ByteBuffer 写入模式2.2 ByteBuffer 读取模式2.3 ByteBuffer 写入模式切换为读取模式2.4 clear() 与 compact() 方法2.5 ByteBuffer 使用案例 总结 前言 回顾Netty系列文章: Netty 概述(一&…...
Python - 面向对象编程 - 实例方法、静态方法、类方法
实例方法 在类中定义的方法默认都是实例方法,前面几篇文章已经大量使用到实例方法 实例方法栗子 class PoloBlog:def __init__(self, name, age):print("自动调用构造方法")self.name nameself.age agedef test(self):print("一个实例方法&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
