面试官:MySQL自增主键一定是连续的吗?
测试环境:
MySQL版本:8.0
数据库表:T (主键id,唯一索引c,普通字段d)

如果你的业务设计依赖于自增主键的连续性,这个设计假设自增主键是连续的。但实际上,这样的假设是错的,因为自增主键不能保证连续递增。
一、自增值的属性特征:
1. 自增主键值是存储在哪的?
MySQL5.7版本
在 MySQL 5.7 及之前的版本,自增值保存在内存里,并没有持久化。每次重启后,第一次打开表的时候,都会去找自增值的最大值 max(id),然后将 max(id)+1 作为这个表当前的自增值。
MySQL8.0之后版本
在 MySQL 8.0 版本,将自增值的变更记录在了 redo log 中,重启的时候依靠 redo log 恢复重启之前的值。
可以通过看表详情查看当前自增值,以及查看表参数详情AUTO_INCREMENT值(AUTO_INCREMENT就是当前数据表的自增值)

2. 自增主键值的修改机制?
在表t中,我定义了主键id为自增值,在插入一行数据的时候,自增值的行为如下:
-
如果插入数据时 id 字段指定为 0、null 或未指定值,那么就把这个表当前的
AUTO_INCREMENT值填到自增字段; -
如果插入数据时 id 字段指定了具体的值,就直接使用语句里指定的值。
根据要插入的值和当前自增值的大小关系,自增值的变更结果也会有所不同。假设,某次要插入的值是 X,当前的自增值是 Y。
-
如果 X<Y,那么这个表的自增值不变;
-
如果 X≥Y,就需要把当前自增值修改为新的自增值。
二、新增语句自增主键是如何变化的:
我们执行以下SQL语句,来观察自增主键是如何进行变化的
insert into t values(null, 1, 1);
流程图如下所示
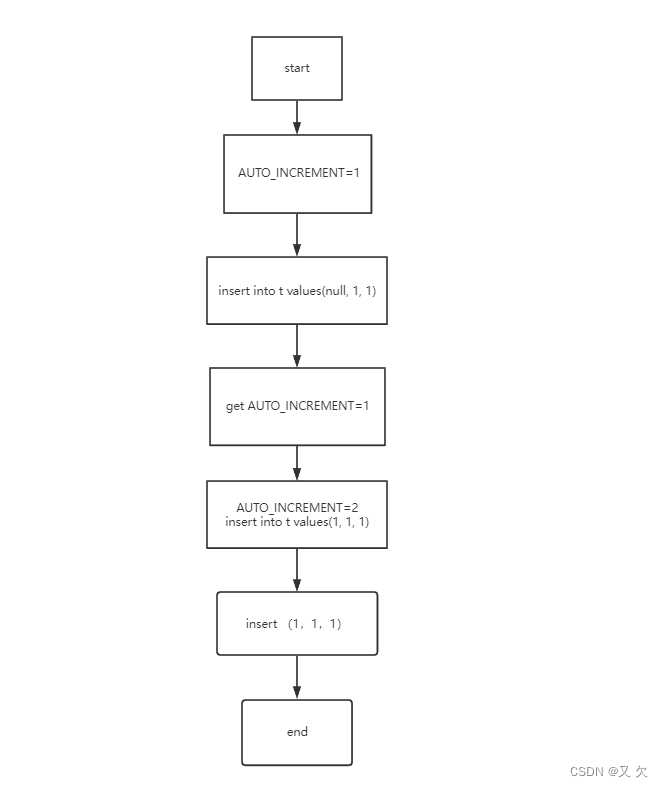
流程步骤:
-
AUTO_INCREMENT=1 (表示下一次插入数据时,如果需要自动生成自增值,会生成 id=1。)
-
insert into t values(null, 1, 1) (执行器调用 InnoDB 引擎接口写入一行,传入的这一行的值是 (0,1,1))
-
get AUTO_INCREMENT=1 (InnoDB 发现用户没有指定自增 id 的值,获取表 t 当前的自增值 1 )
-
AUTO_INCREMENT=2 insert into t values(1, 1, 1) (将传入的行的值改成 (1,1,1),并把自增值改为2)
-
insert (1,1,1) 执行插入操作,至此流程结束
大家可以发现,在这个流程当中是先进行自增值的+1,在进行新增语句的执行的。大家可以发现这个操作并没有进行原子操作,如果SQL语句执行失败,那么自增是不是就不会连续了呢?
三、自增主键值不连续情况:(唯一主键冲突)
当我执行以下SQL语句时
insert into t values(null, 1, 1);
第一次我们可以进行新增成功,根据自增值的修改机制。如果插入数据时 id 字段指定为 0、null 或未指定值,那么就把这个表当前的 AUTO_INCREMENT 值填到自增字段;
当我们第二次在执行以下SQL语句时,就会出现错误。因为我们表中c字段是唯一索引,会出现Duplicate key error错误导致新增失败。

例如:
-
AUTO_INCREMENT=2 (表示下一次插入数据时,如果需要自动生成自增值,会生成 id=2。)
-
insert into t values(null, 1, 1) (执行器调用 InnoDB 引擎接口写入一行,传入的这一行的值是 (0,1,1))
-
get AUTO_INCREMENT=2 (InnoDB 发现用户没有指定自增 id 的值,获取表 t 当前的自增值 2 )
-
AUTO_INCREMENT=3 insert into t values(2, 1, 1) (将传入的行的值改成 (2,1,1),并把自增值改为3)
-
insert (2,1,1) 执行插入操作,由于已经存在 c=1 的记录,所以报
Duplicate key error,语句返回。
可以看到,这个表的自增值改成 3,是在真正执行插入数据的操作之前。这个语句真正执行的时候,因为碰到唯一键 c 冲突,所以 id=2 这一行并没有插入成功,但也没有将自增值再改回去。所以,在这之后,再插入新的数据行时,拿到的自增 id 就是 3。也就是说,出现了自增主键不连续的情况。
四、自增主键值不连续情况:(事务回滚)
其实事务回滚原理也和上面一样,都是因为异常导致新增失败,但是自增值没有进行回退。
五、自增主键值不连续情况:(批量插入)
批量插入数据的语句,MySQL 有一个批量申请自增 id 的策略:
-
语句执行过程中,第一次申请自增 id,会分配 1 个;
-
1 个用完以后,这个语句第二次申请自增 id,会分配 2 个;
-
2 个用完以后,还是这个语句, 第三次申请自增 id,会分配 4 个;
-
依此类推,同一个语句去申请自增 id,每次申请到的自增 id 个数都是上一次的两倍。
执行以下SQL语句(在表t中先新增了4条数据,在创建表tt把表t数据进行批量新增)
insert into t values(null, 1,1);
insert into t values(null, 2,2);
insert into t values(null, 3,3);
insert into t values(null, 4,4);
create table tt like t;
insert into tt(c,d) select c,d from t;insert into tt values(null, 5,5);
第一次申请到了 id=1,第二次被分配了 id=2 和 id=3, 第三次被分配到 id=4 到 id=7。当我们再执行 insert into t2 values(null, 5,5),实际上插入的数据就是(8,5,5),出现了自增主键不连续的情况。
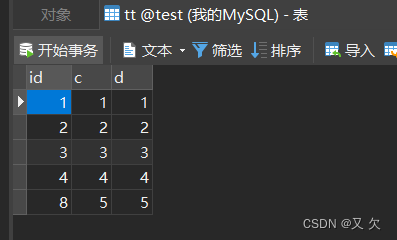
六、自增主键值的优化
1.什么是自增锁
自增锁是一种比拟非凡的表级锁。并且在事务向蕴含了 AUTO_INCREMENT 列的表中新增数据时就会去持有自增锁,假如事务 A 正在做这个操作,如果另一个事务 B 尝试执行 INSERT语句,事务 B 会被阻塞住,直到事务 A 开释自增锁。
2.自增锁有哪些优化
在 MySQL 5.0 版本的时候,自增锁的范围是语句级别。也就是说,如果一个语句申请了一个表自增锁,这个锁会等语句执行结束以后才释放。显然,这样设计会影响并发度。在MySQL 5.1.22 版本引入了一个新策略,新增参数 innodb_autoinc_lock_mode,默认值是 1。
传统模式(Traditional)
这个参数的值被设置为 0 时,表示采用之前 MySQL 5.0 版本的策略,即语句执行结束后才释放锁;
传统模式他可以保证数据一致性,但是如果有多个事务并发的执行 INSERT 操作,AUTO-INC的存在会使得 MySQL 的性能略有降落,因为同时只能执行一条 INSERT 语句。
间断模式(Consecutive)
这个参数的值被设置为 1 时:普通 insert 语句,自增锁在申请之后就马上释放;类似 insert … select 这样的批量插入数据的语句,自增锁还是要等语句结束后才被释放;
间断模式他可以保证数据一致性,但是如果有多个事务并发的执行 INSERT 批量操作时,就会进行锁等待状态。如果我们业务插入数据量很大时,这个时候MySQL的性能就会大大下降。
穿插模式(Interleaved)
这个参数的值被设置为 2 时,所有的申请自增主键的动作都是申请后就释放锁。
穿插模式他没有进行任何的上锁设置。在一定情况下是保证了MySQL的性能,但是他无法保证数据的一致性。如果我们在穿插模式下进行主从复制时,如果你的binlog格式不是row格式,主从复制就会出现不一致。
七、MySQL8.0做了哪些优化
在MySQL8.0之后版本,已经默认设置为 innodb_autoinc_lock_mode=2 , binlog_format=row.。这样更有利与我们在 insert … select 这种批量插入数据的场景时,既能提升并发性,又不会出现数据一致性问题。
相关文章:

面试官:MySQL自增主键一定是连续的吗?
测试环境: MySQL版本:8.0 数据库表:T (主键id,唯一索引c,普通字段d) 如果你的业务设计依赖于自增主键的连续性,这个设计假设自增主键是连续的。但实际上,这样的假设是错的…...

2023ACP世界大赛教育者论坛:让职业教育直面AI机遇与挑战
“AI技术的普及对创意行业和教育带来的影响和变革-2023 Adobe Certified Professional教育者论坛”在苏州西交利物浦大学成功举办。 本次论坛,由Adobe Certified Professional 世界大赛中国赛区组委会主办,联动了来自院校、海内外杰出的创意公司及国际知…...
Unity基础 音频组件以及音频播放
在游戏开发中,声音是一个重要的环节。Unity中的声音组件可以帮助开发者轻松地控制游戏中音频的播放、音量、循环等属性,从而实现更好的游戏体验。本文将详细介绍Unity声音组件的相关概念和技术,以及其在游戏、影视等领域的广泛应用和发展前景…...
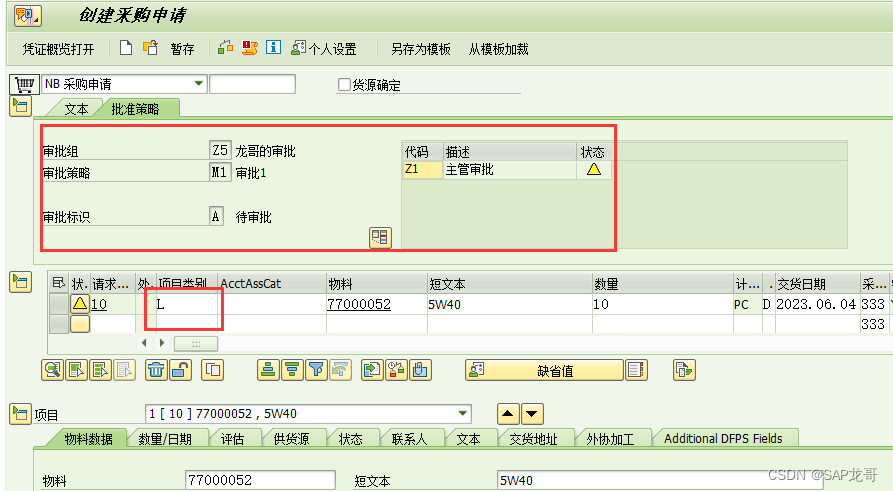
SAP-MM-采购申请审批那些事!
1、ME55不能审批删除行项目的PR 采购申请审批可以设置行项目审批或抬头审批。如果设置为抬头审批时,ME55集中审批时,就会发现有些采购申请时不能审批的, 那么这些采购申请时真的不需要审批么?不是的,经过核对这些采购申…...

专业解读财务共享实现财务数智化转型的有效路径
近年来,随着数字经济的飞速发展,各大企业全面开启数智化转型之路,作为企业数智化转型的重要内容,财务数智化转型始于财务共享服务。然而,财务共享建设并不是一蹴而就的,如何通过财务共享实现财务数智化转型…...
九章云极DataCanvas公司诚邀您共享AI基础软件前沿技术盛宴
“杭州通用人工智能论坛暨AIIA人工智能产业发展大会”将于2023年5月30日-31日在杭州举办。本次人工智能产业发展大会由中国信息通信研究院、中国人工智能产业发展联盟主办,杭州城西科创大走廊管委会、杭州市经济和信息化局、杭州未来科技城管理委员会、人工智能关键…...

【高级语言程序设计(一)】第 10 章:文件
目录 一、文件概述 (1)文件定义 (2)文件命名 (3)文件分类 ① 按照文件的内容划分 ② 按照文件的组织形式划分 ③ 按照文件的存储形式划分 ④ 按照文件的存储介质划分 (4)文…...

Android 宿主启动插件中的Activity和Service
在宿主App中加载插件App中的四大组件,需要以下几个步骤: 1. 预先在宿主的AndroidManifest文件中声明插件中的四大组件 <?xml version"1.0" encoding"utf-8"?> <manifest xmlns:android"http://schemas.android.co…...
00后卷王自述,我真的很卷吗?
前段时间我去面试了一个软件测试公司,成功拿到了offer,薪资也从10k涨到了18k,对于工作都还没两年的我来说,还是比较满意的,毕竟有些工作了3到4年的可能还没有我的高。 在公司一段时间后大家都说我是卷王,其…...

真题详解(树的结点)-软件设计(八十四)
真题详解(汇总)-软件设计(八十三)https://blog.csdn.net/ke1ying/article/details/130856130?spm1001.2014.3001.5501 COCOMOII估算不包括_____。 对象点 B.功能点 C.用例数 D.源代码行 答案:C 语法翻译是一种ÿ…...

LDA算法实现鸢尾花数据集降维
目录 1. 作者介绍2. LDA降维算法2.1 基本概念2.2 算法流程 3. LDA算法实现3.1 数据集介绍3.2 代码实现3.3 结果展示 1. 作者介绍 唐杰,男,西安工程大学电子信息学院,2022级研究生 研究方向:机器视觉与人工智能 电子邮件ÿ…...

深入理解Linux虚拟内存管理
系列文章目录 Linux 内核设计与实现 深入理解 Linux 内核(一) 深入理解 Linux 内核(二) Linux 设备驱动程序(一) Linux 设备驱动程序(二) Linux 设备驱动程序(三…...
自动化测试框架、Python面向对象以及POM设计模型简介
目录 1 自动化测试框架概述 2 自动化测试框架需要的环境 3 自动化测试框架设计思想:Python面向对象 4 自动化测试框架设计思想:POM(Page Object Model)页面对象模型 1 自动化测试框架概述 所谓的框架其实就是一个解决问题…...
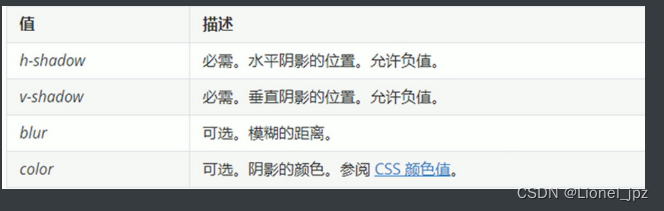
【CSSpart4--盒子模型】
CSSpart4--盒子模型 网页布局的三大核心:盒子模型,浮动,定位网页布局的过程(本质):盒子模型的组成四部分:边框,内容,内边距,外边距 一 、盒子边框border:1.1 …...
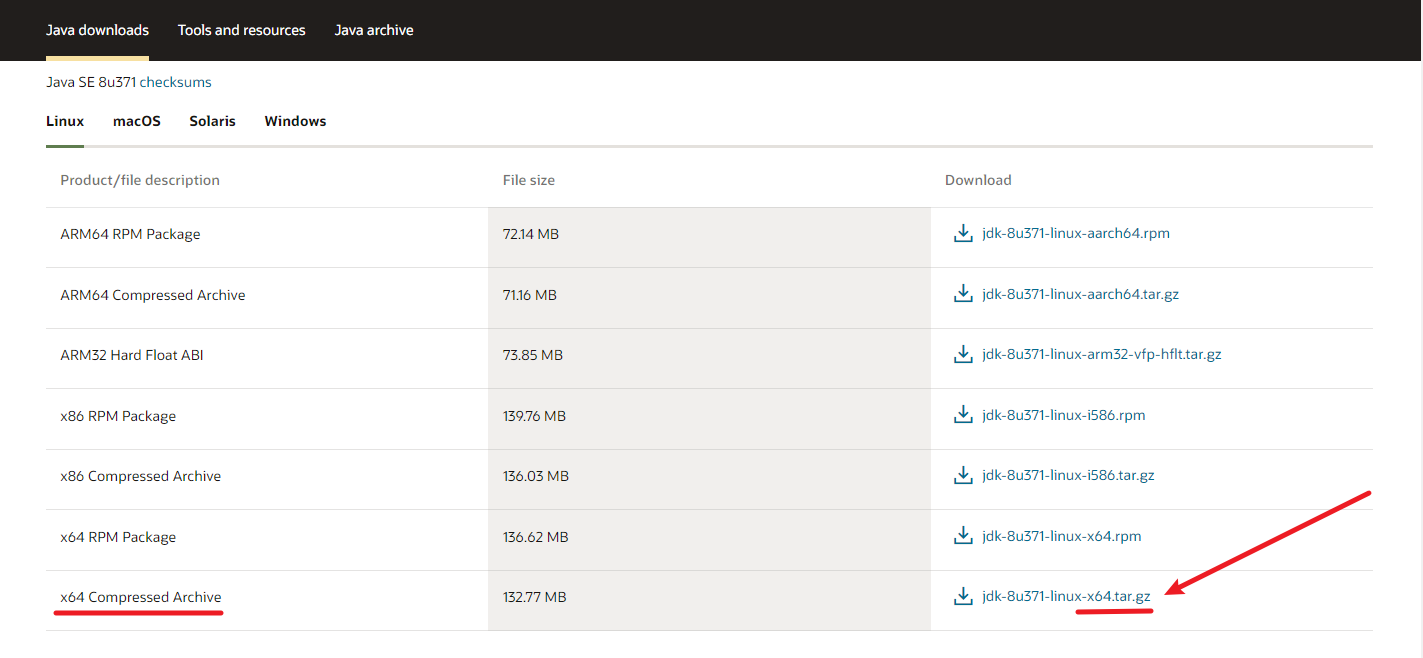
Linux - Java 8 入门安装与重装教程集锦
一、入门初始安装 1. 具体安装教程 1. linux 系统中如何安装java环境(通过tar.gz文件) 安装包下载链接 Java 的 tar.gz 安装包下载链接传送门 Linux 系统的 Java 环境变量配置教程 1. linux查看java版本,以及配置java home 2. Linux环…...
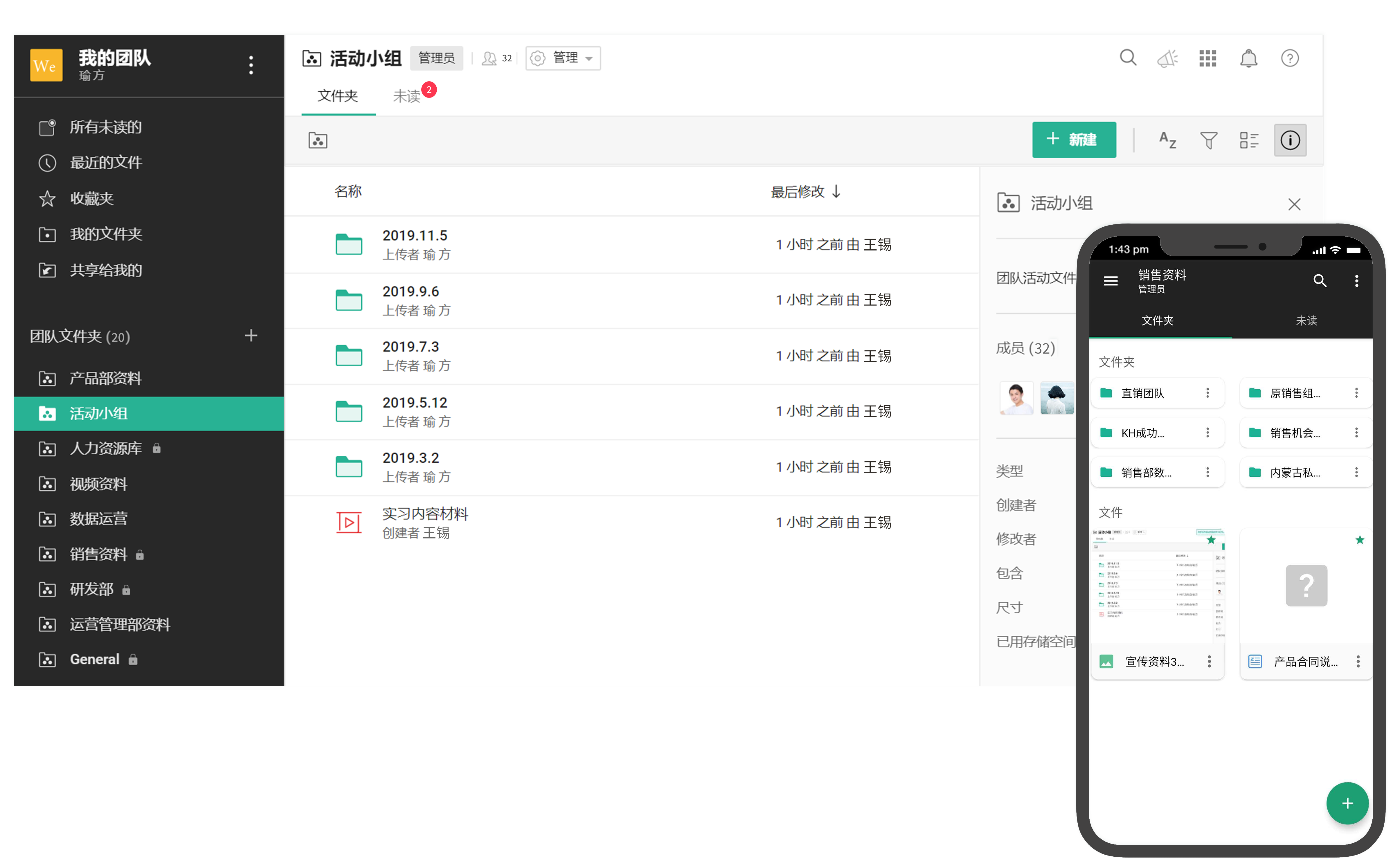
2023年最新企业网盘排行榜出炉
随着云计算技术的不断发展,企业日常工作中大量的资料、文档等信息需要实现集中管理,此时企业网盘工具就应运而生。企业网盘是一种可用于企业内部管理、团队协作及文件共享的云存储平台,能够极大提高企业办公效率和安全性。 一、企业网盘的帮助…...

C++内存分类
内存分配方式(内存布局): 内存5分类 堆、栈、自由存储区、全局/静态存储区、常量存储区 (1)栈:内存由编译器在需要时自动分配和释放。通常用来存储局部变量和函数参数,函数调用后返回的地址。(为运行函数而…...

不是说00后已经躺平了吗,怎么还是这么卷.....
都说00后已经躺平了,但是有一说一,该卷的还是卷。 前段时间我们部门就来了个00后,工作都还没两年,跳到我们公司起薪20K,都快接近我了。 后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。最近和…...

国内免费版ChatGPT
目录 前言:网站大全 1. ChatGPT是什么 2. ChatGPT的发展历程 3. ChatGPT对程序员的影响 4. ChatGPT对普通人的影响 5. ChatGPT的不足之处 前言:网站大全 AI文本工具站 (laicj.cn) ——gpt-3.5 功能强大(推荐) Chatgpt在线网页版-…...

常用本地事务和分布式事务解决方案模型
目录 1 DTP模型2 2PC2.1 方案简介2.2 处理流程2.2.1 阶段1:准备阶段2.2.2 阶段2:提交阶段 2.3 方案总结 3 3PC3.1 方案简介3.2 处理流程3.2.1 阶段1:canCommit3.2.2 阶段2:preCommit3.3.3 阶段3:do Commit 3.3 方案总结…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
