算法基础学习笔记——⑩DFS与BFS\树与图
✨博主:命运之光
✨专栏:算法基础学习

目录
DFS与BFS\树与图
✨DFS
✨BFS
🍓宽搜流程图如下:
🍓宽搜流程:
🍓广搜模板
✨树与图
🍓树是特殊的图(连通无环的图)
🍓树与图的存储:
🍓用宽搜框架来搜索图:
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
DFS与BFS\树与图
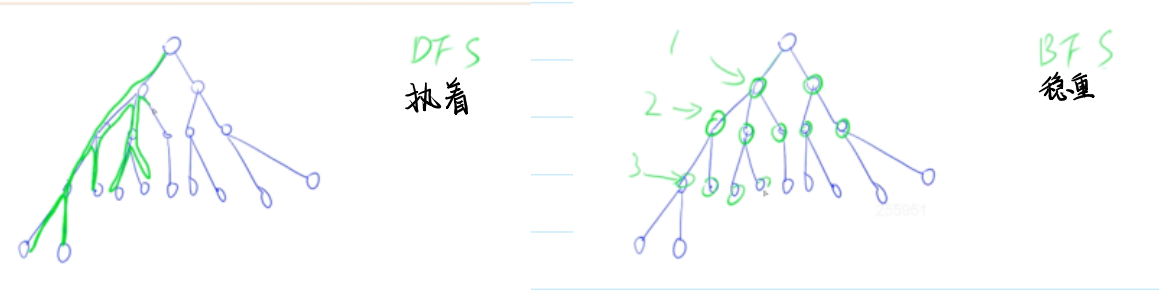
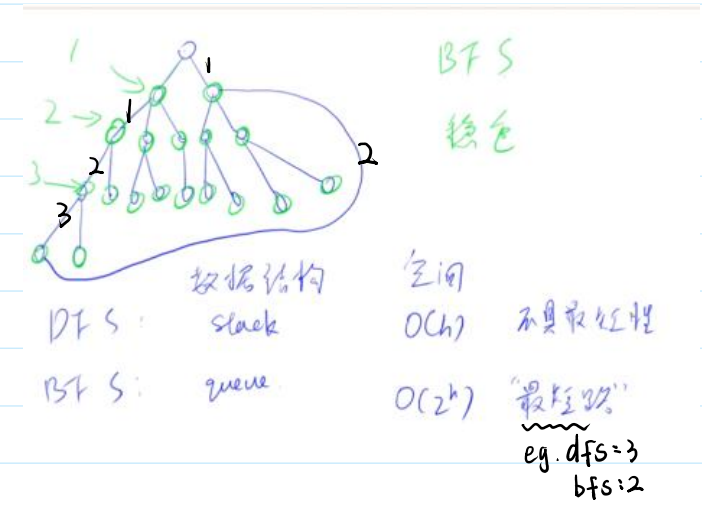
✨DFS
//回溯,剪枝
当使用深度优先搜索(DFS)回溯算法来搜索图时,我们需要考虑以下几个步骤:
- 初始化数据结构:创建一个栈(通常使用先进后出的原则)来存储待探索的节点,以及一个集合(通常使用哈希集合或集合)来记录已访问的节点。
- 将起始节点放入栈中,并将其标记为已访问。
- 进入循环,直到栈为空:
-
- 从栈中取出一个节点。
- 检查该节点是否为目标节点。如果是,则搜索完成,返回结果。
- 如果不是目标节点,则将其所有未访问过的邻居节点加入栈,并标记为已访问。
- 继续下一轮循环。
- 如果循环结束时仍未找到目标节点,则图中不存在目标节点。

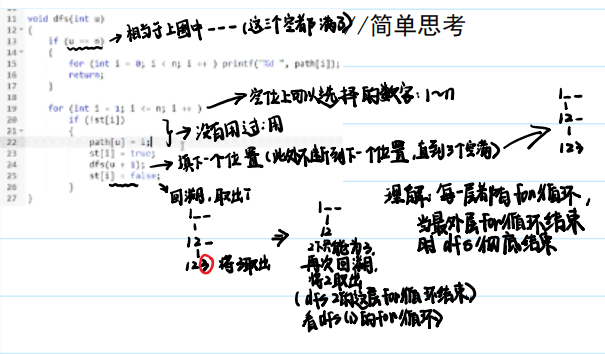
剪枝:可以提前判断当前方案一定不合法,就不用往下搜
✨BFS

🍓宽搜流程图如下:

🍓宽搜流程:

🍓广搜模板
q.push(初始状态);
while(q.empty()){a=q.front();q.pop();for(枚举a的所有可达状态v){if(本状态v合法){执行标记操作;q.push(v);}}
}
连通块问题:
例题:全球变暖
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1005;
bool v[N][N],book[N*N];
char a[N][N];
int n,w[N][N],s,cnt;
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
typedef struct node
{int x,y;
}node;
queue<node>q;
bool check(int x,int y)
{if(x<1||x>n||y<1||y>n)return false;return true;
}
bool judge(int x,int y)
{if(check(x+1,y)&&a[x+1][y]=='.')return false;if(check(x,y+1)&&a[x][y+1]=='.')return false;if(check(x-1,y)&&a[x-1][y]=='.')return false;if(check(x,y-1)&&a[x][y-1]=='.')return false;return true;
}
void bfs()
{while(!q.empty()){node head,tail;head=q.front();q.pop();for(int i=0;i<4;i++){tail.x=head.x+dx[i];tail.y=head.y+dy[i];if(check(tail.x,tail.y)&&a[tail.x][tail.y]=='#'&&w[tail.x][tail.y]==0){w[tail.x][tail.y]=cnt;q.push(tail);}}}
}
int main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i][j]=='#'&&w[i][j]==0){cnt++;w[i][j]=cnt;node tmp={i,j};q.push(tmp);bfs();}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i][j]=='#'){if(judge(i,j)){book[w[i][j]]=true;}}}}for(int i=1;i<=cnt;i++){if(book[i]==true){s++;}}cout<<cnt-s;return 0;
}问题2:
两个BFS
例题:Fire
/*
预处理:预处理出火传染到(i,j)点的最早时间
人在去想要走到(i,j)点时,到(i,j)点的时刻一定要小于火最早到(i,j)的s时刻
*/
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N=1000+5;
const int INF=0x3f3f3f3f;
typedef struct Node{int x,y;int t;
}Node;
int t,n,m;
int ti[N][N];//ti[i][j]是火最早到(i,j)的时间
char a[N][N];
queue<Node> fq,q;
bool vis[N][N];
int _next[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
bool judge(int x,int y)
{if(x<1||x>n||y<1||y>m)return false;return true;
}
void FireBFS()
{Node _new;while(!fq.empty()){Node tp=fq.front();fq.pop();for(int i=0;i<4;i++){_new.x=tp.x+_next[i][0];_new.y=tp.y+_next[i][1];if(judge(_new.x,_new.y)&&a[_new.x][_new.y]=='.'&&ti[_new.x][_new.y]==INF){_new.t=tp.t+1;ti[_new.x][_new.y]=_new.t;fq.push(_new);}}}
}
int ManBFS(){Node _new;while(!q.empty()){Node tp=q.front();q.pop();if(tp.x==1||tp.x==n||tp.y==1||tp.y==m){return tp.t+1;}for(int i=0;i<4;i++){_new.x=tp.x+_next[i][0];_new.y=tp.y+_next[i][1];if(judge(_new.x,_new.y)&&a[_new.x][_new.y]=='.'&&!vis[_new.x][_new.y]){_new.t=tp.t+1;if(_new.t<ti[_new.x][_new.y]){vis[_new.x][_new.y]=true;q.push(_new);}}}}return -1;
}
void init(){memset(ti,0x3f,sizeof(ti));memset(vis,false,sizeof(vis));while(!fq.empty())fq.pop();while(!q.empty())q.pop();
}
int main(){cin>>t;while(t--){init();cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='F'){Node tmp={i,j,0};ti[i][j]=0;fq.push(tmp);}else if(a[i][j]=='J'){Node tmp={i,j,0};vis[i][j]=true;q.push(tmp);}}}FireBFS();int ans=ManBFS();if(ans==-1)cout<<"IMPOSSIBLE"<<endl;elsecout<<ans<<endl;}
}
/*
2
4 4
####
#JF#
#..#
#..#
3 3
###
#J.
#.F
*/✨树与图
🍓树是特殊的图(连通无环的图)


🍓树与图的存储:
树是一种特殊的图,与图的存储方式相同。
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
(1) 邻接矩阵:g[a][b] 存储边a->b
(2) 邻接表:
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;
// 添加一条边a->b
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);树与图的遍历:
时间复杂度 O(n+m)O(n+m), nn 表示点数,mm 表示边数
(1) 深度优先遍历

int dfs(int u)
{st[u] = true; // st[u] 表示点u已经被遍历过for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (!st[j]) dfs(j);}
}(2) 宽度优先遍历

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{int t = q.front();q.pop();for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true; // 表示点j已经被遍历过q.push(j);}}
}🍓用宽搜框架来搜索图:
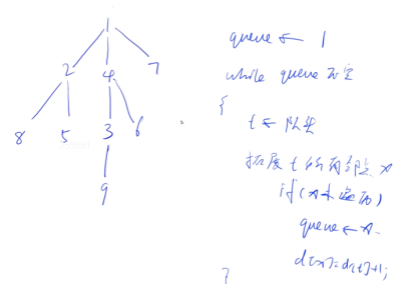
当使用宽度优先搜索(BFS)框架搜索图时,我们可以按照以下步骤进行操作:
- 选择一个起始节点,并将其添加到队列中,同时将其标记为已访问。
- 重复以下步骤直到队列为空:
-
- 从队列中取出一个节点作为当前节点。
- 检查当前节点是否满足搜索条件。如果是,则返回结果或执行相应操作。
- 遍历当前节点的所有相邻节点。
- 对于每个未被访问的相邻节点,将其添加到队列中,并将其标记为已访问。
- 如果队列为空且没有找到满足条件的节点,则搜索结束,可以返回相应的结果或执行其他操作。
🍓以下是使用宽度优先搜索框架在C++中搜索图的示例代码:
#include <iostream>
#include <queue>
#include <unordered_set>
#include <unordered_map>
#include <vector>
bool bfs(const std::unordered_map<char, std::vector<char>>& graph, char startNode, char targetNode) {std::queue<char> queue; // 创建一个队列std::unordered_set<char> visited; // 创建一个集合,用于记录已访问的节点queue.push(startNode); // 将起始节点放入队列visited.insert(startNode); // 标记起始节点为已访问while (!queue.empty()) {char node = queue.front(); // 从队列中取出一个节点queue.pop();if (node == targetNode) // 检查是否为目标节点return true;const std::vector<char>& neighbors = graph.at(node); // 获取当前节点的邻居节点for (char neighbor : neighbors) {if (visited.find(neighbor) == visited.end()) { // 如果邻居节点未被访问过queue.push(neighbor); // 将邻居节点加入队列visited.insert(neighbor); // 标记邻居节点为已访问}}}return false; // 循环结束,未找到目标节点
}
int main() {std::unordered_map<char, std::vector<char>> graph = {{'A', {'B', 'C'}},{'B', {'D', 'E'}},{'C', {'F'}},{'D', {}},{'E', {'F'}},{'F', {}}};char startNode = 'A';char targetNode = 'F';bool result = bfs(graph, startNode, targetNode);if (result)std::cout << "The target node '" << targetNode << "' is reachable from the start node '" << startNode << "'.\n";elsestd::cout << "The target node '" << targetNode << "' is not reachable from the start node '" << startNode << "'.\n";return 0;
}在上述代码中,使用std::unordered_map来表示图的邻接表,其中键是节点,值是该节点的邻居节点列表。还使用std::queue来作为队列存储待探索的节点,std::unordered_set用于记录已访问的节点。
注意,上述代码仅为示例,假设图中的节点标识为字符('A', 'B', 'C'等),您可以根据实际情况进行修改和适应。
相关文章:

算法基础学习笔记——⑩DFS与BFS\树与图
✨博主:命运之光 ✨专栏:算法基础学习 目录 DFS与BFS\树与图 ✨DFS ✨BFS 🍓宽搜流程图如下: 🍓宽搜流程: 🍓广搜模板 ✨树与图 🍓树是特殊的图(连通无环的图&am…...

chatgpt赋能python:Python中可迭代对象的介绍
Python中可迭代对象的介绍 Python是一种高级编程语言,它具有简单易学、可读性强、功能强大等特点,成为了数据科学、机器学习、Web开发等领域的热门选择。Python中有很多重要的概念和功能,其中之一就是支持可迭代对象的概念。 在Python中&am…...
报表控件FastReport使用指南——如何打开WebP格式的图片
FastReport 是功能齐全的报表控件,可以帮助开发者可以快速并高效地为.NET,VCL,COM,ActiveX应用程序添加报表支持,由于其独特的编程原则,现在已经成为了Delphi平台最优秀的报表控件,支持将编程开…...
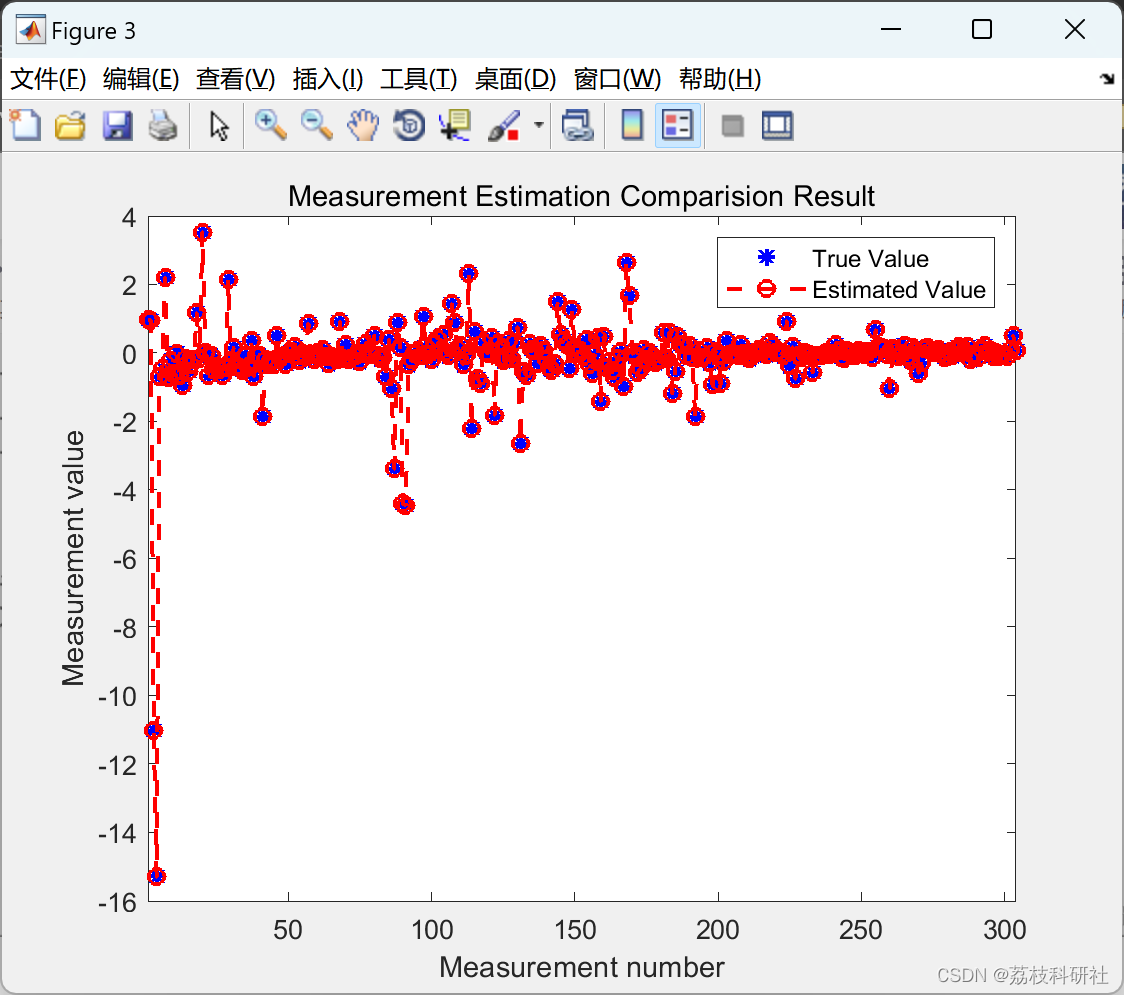
【鲁棒、状态估计】用于电力系统动态状态估计的鲁棒迭代扩展卡尔曼滤波器研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
整理6个超好用的在线编辑器!
随着 Web 开发对图像可扩展性、响应性、交互性和可编程性的需求增加,SVG 图形成为最适合 Web 开发的图像格式之一。它因文件小、可压缩性强并且无论如何放大或缩小,图像都不会失真而受到欢迎。然而,为了编辑 SVG 图像,需要使用 SV…...

ArcGIS10.8下载及安装教程(附安装步骤)
谷歌云: https://drive.google.com/drive/folders/10igu7ZSMaR0v0WD7-2W-7ADJGMUFc2ze?uspsharing ArcGIS10.8 百度网盘: https://pan.baidu.com/s/1s5bL3QsCP5sgcftCPxc88w 提取码:kw4j 阿里云: https://www.aliyundriv…...
AI智能照片编辑:AI Photo for Mac
AI Photo是一款Mac平台上的智能照片编辑软件,它基于人工智能技术,可以帮助用户快速、轻松地对照片进行编辑和美化。AI Photo提供了多种智能修复和美化功能,包括自动调整色彩、对比度、亮度、清晰度等,使得照片的质量得到有效提升。…...
Tuxera for Mac2023中文版读写硬盘U盘工具
在日常生活中,我们使用Mac时经常会遇到外部设备不能正常使用的情况,如:U盘、硬盘、软盘等等一系列存储设备,而这些设备的格式大多为NTFS,Mac系统对NTFS格式分区存在一定的兼容性问题,不能正常读写。 那么什…...

项目遇到的实际需求: java从信任所有证书到对server证书进行校验
最近项目上开发了一个rest api,放在了一台linux服务器上,并且启用了https连接;在另一台服务器上写了一个功能需要去调用linux机器上的api。 项目里面自己封装了一个HttpsClient的类,用来发送https请求,并且在里面重写了…...

使用JS来实现轮播图的效果
最好今天分享一个使用JS制作的轮播图效果 个人名片: 😊作者简介:一名大一在校生,web前端开发专业 🤡 个人主页:几何小超 🐼座右铭:懒惰受到的惩罚不仅仅是自己的失败,…...

Springboot +spring security,自定义认证和授权异常处理器
一.简介 在Spring Security中异常分为两种: AuthenticationException 认证异常AccessDeniedException 权限异常 我们先给大家演示下如何自定义异常处理器,然后再结合源码帮助大家进行分析 二.创建项目 如何创建一个SpringSecurity项目,前…...
 - FROM 指令详解)
Dockerfile(1) - FROM 指令详解
FROM 指明当前的镜像基于哪个镜像构建dockerfile 必须以 FROM 开头,除了 ARG 命令可以在 FROM 前面 FROM [--platform<platform>] <image> [AS <name>]FROM [--platform<platform>] <image>[:<tag>] [AS <name>]FROM […...
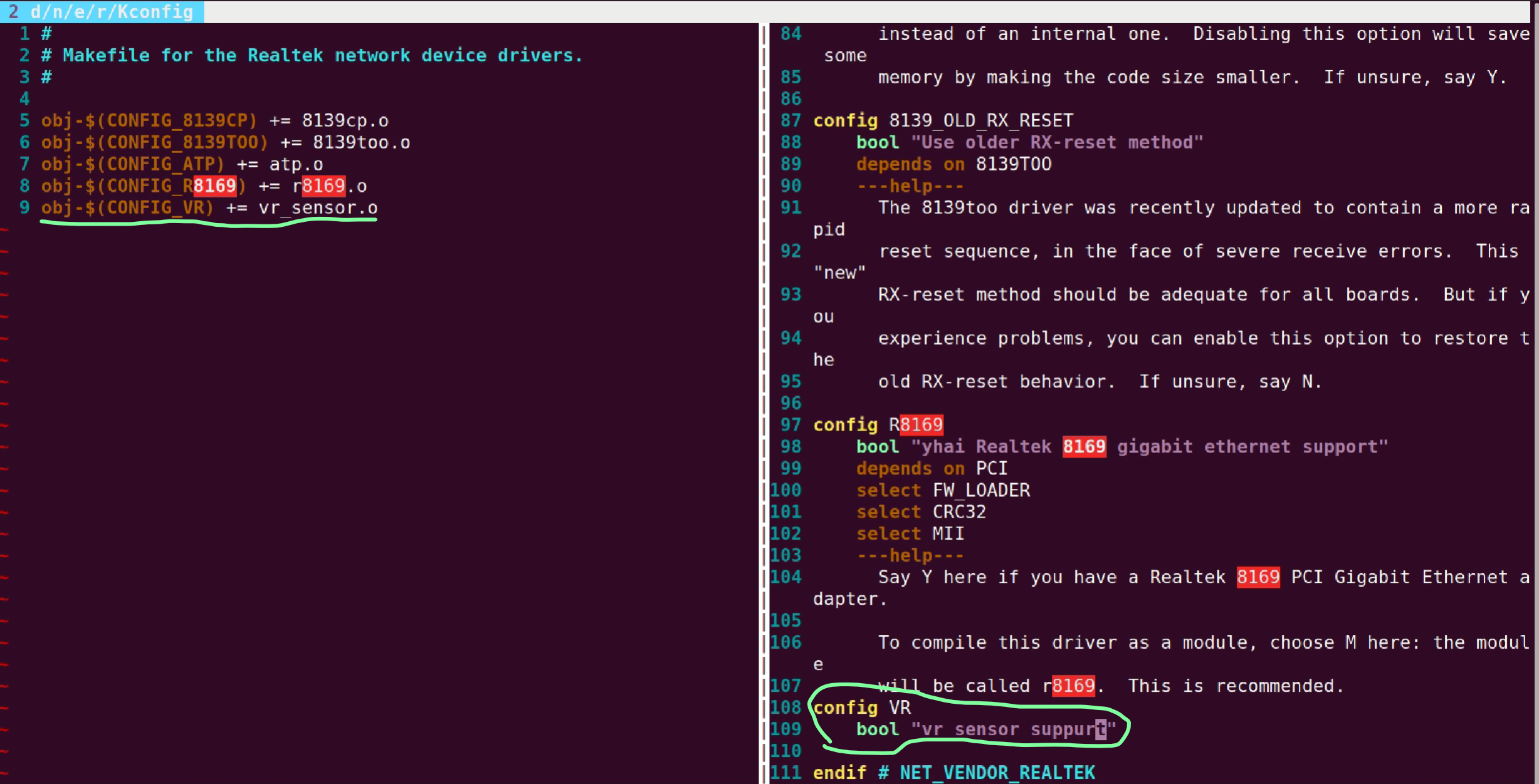
【嵌入式Linux】源码菜单配置 | 编译 | 菜单配置的实现 | 源码编译的实现
源码配置编译 源码配置编译,要把中间各个环节都理清楚 厂商把自己增加的东西专门放了个文件独立,方便开发者发现变化 1.菜单配置 移植的第一步,就是选配,通过make menuconfig图形化界面选配 //载入配置 $ make ARCHarm64 tegra_defconfi…...
python自动化爬虫实战
python自动化爬虫实战 偶然的一次机会再次用到爬虫,借此机会记录一下爬虫的学习经历,方便后续复用。 需求:爬取网站数据并存入的csv文件中,总体分为两步 爬取网站数据存到到csv文件中 1、配置爬虫环境 1.1、下载自动化测试驱动 …...

LVGL-最新版本及其版本定义标准
lvgl的最新版本是9.0.0,处于开发分支中。 稳定版本是8.3.0. 建议一般开发使用稳定版8.3.0. .\lvgl.h定义了当前版本 /*************************** CURRENT VERSION OF LVGL ***************************/ #define LVGL_VERSION_MAJOR 8 #define LVGL_VERSION_MINO…...

ORB_SLAM2算法中如何计算右目和左目两个特征点的是否匹配?
文章目录 if(kpR.octave<levelL-1 || kpR.octave>levelL+1)const int &levelL = kpL.octave;if(uR>=minU && uR<=maxU)const cv::Mat &dR = mDescriptorsRight.row(iR);const int dist = ORBmatcher::DescriptorDistance(dL,dR);筛选最佳匹配特征点…...

Android 12.0系统Settings主页去掉搜索框
1.概述 在12.0定制化开发中,在系统原生设置中主页的搜索框是要求去掉的,不需要搜索功能,所以首选看下布局文件 看下搜索框是哪个布局,然后隐藏到布局,达到实现功能的目的 2.系统Settings主页去掉搜索框的主要代码 packages/apps/Settings/src/com/android/settings/home…...

电脑数据丢失如何恢复
随着电脑使用的日益普及,数据丢失成为了很多用户不得不面对的问题。数据丢失的原因有很多,例如误删除文件、磁盘格式化、电脑病毒等等。一旦发生数据丢失的情况,我们就需要利用专业的数据恢复工具来尽快找回被丢失的数据。下面我们就来详细介…...
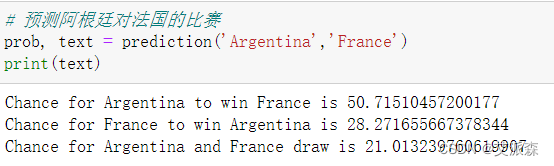
大数据分析案例-基于决策树算法构建世界杯比赛预测模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

Python 图形界面框架 PyQt5 使用指南
Python 图形界面框架 PyQt5 使用指南 使用Python开发图形界面的软件其实并不多,相对于GUI界面,可能Web方式的应用更受人欢迎。但对于像我一样对其他编程语言比如C#或WPF并不熟悉的人来说,未必不是一个好的工具。 常见GUI框架 PyQt5[1]&#…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
