二叉排序树的查找、插入、删除
目录
二叉排序树的定义
二叉排序树的查找
二叉排序树的插入
二叉排序树的定义
二叉排序树的定义
二叉排序树(Binary Sort Tree, BST),也称二叉查找树。
二叉排序树或者是一棵空树,或者是一棵具有下列特性的非空二叉树:
1) 若左子树非空,则左子树上所有结点关键字均小于根结点的关键字值;
2) 若右子树非空,则右子树上所有结点关键字均大于根结点的关键字值;
3) 左、右子树本身也分别是一棵二叉排序树。
由定义可知,二叉排序树是一个递归的数据结构,可以方便的使用递归算法对二叉排序树进行各种运算。
根据二叉树的定义,可得左子树结点值 < 根结点值 < 右子树结点值。
所以,对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
二叉排序结点结构:
typedef struct BiTNode
{int data;struct BiTNode *left, *right;
}BiTNode,*Bitree;二叉排序树的查找
二叉排序树的查找是从根结点开始的,沿某个分支逐层向下进行比较的过程。
其查找过程描述如下:若二叉排序树非空,则将给定值与根结点的关键字比较,若相等,则查找成功;若不等,则当根结点的关键字值大于给定关键字值时,在根结点的左子树中查找;否则在根结点的右子树中查找。
递归查找:
Bitree SearchBST(Bitree root, int key){if(root->data == key){return root;}else if(key< root->data){return SearchBST(root->left, key);}else{return SearchBST(root->right, key);}
}
非递归查找
//查找的非递归算法
Bitree SearchBST(Bitree root, int key){Bitree p = root;while(p!=NULL && p->data!=key){if(key< p->data)p = p->left;elsep = p->right;}return p;
}
二叉排序树的插入
//插入的递归算法
Bitree Insert(Bitree root, int x) {if (root == NULL) {root = (Bitree)malloc(sizeof(BiTNode));root->data;root->left = NULL;root->right = NULL;return root;}if (x < root->data) {root->left = Insert(root->left, x);}if (x > root->data) {root->right = Insert(root->right, x);}return root;
}
//插入的非递归算法
void Inser_Node(Bitree &T, int key)
{Bitree parent = NULL;Bitree p = T;Bitree s = (Bitree)malloc(sizeof(BiTNode));s->data = key;s->left = NULL;s->right = NULL;if (T== NULL){T = s;return;}while (p != NULL){parent = p;if (p->data > key)//在左孩子继续查找{p = p->left;}if (p->data < key){p = p->right;}}if (parent->data > key){parent->left = s;}else {parent->right = s;}}根据书上代码,将查找和插入整合:
/****************书上代码***************************/
int SearchBST(Bitree T,int key, Bitree f, Bitree& p)
{if (!T){p = f;return 0;}else if(T->data==key){p = T;printf("有重复");return 1;}else if (T->data > key){return SearchBST(T->left, key, T, p);}else{return SearchBST(T->right, key, T, p);}
}
void InserBST(Bitree& T, int key)
{Bitree p;if (SearchBST(T, key, NULL, p)==0)//查找失败,进行插入{Bitree s =(Bitree) malloc(sizeof(BiTNode));s->data = key;s->left = NULL;s->right = NULL;if (!p){T = s;}else if (key < p->data){p->left = s;//被插入点作为*s左孩子}else {p->right = s;}}
}
相关文章:

二叉排序树的查找、插入、删除
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的定义 二叉排序树的定义 二叉排序树(Binary Sort Tree, BST),也称二叉查找树。 二叉排序树或者是一棵空树,或者是一棵具有下列特性的非空二叉…...
《Opencv3编程入门》学习笔记—第三章
《Opencv3编程入门》学习笔记 记录一下在学习《Opencv3编程入门》这本书时遇到的问题或重要的知识点。 第三章 HighGUI图形用户界面初步 一、图像的载入、显示和输出到文件 (一)OpenCV的命名空间 简单的OpenCV程序标配: #include <o…...
如何从Ubuntu Linux中删除Firefox Snap?
Ubuntu Linux是一款广受欢迎的开源操作系统,拥有强大的功能和广泛的应用程序选择。默认情况下,Ubuntu提供了一种称为Snap的软件打包格式,用于安装和管理应用程序。Firefox是一款流行的开源网络浏览器,而Firefox Snap是Firefox的Sn…...
数学建模的初阶-快速上手
目录 第一步:明确问题 第二步:选择建模方法 第三步:收集数据 第四步:构建数学模型 第五步:模型验证与评估 数学建模软件推荐 统计模型 (1) 线性回归模型 (2) 逻辑回归模型 (3) 时间序列模型 优化模型 (1) …...
)
复习向 C/C++ 编程语言简介和概括(C++复习向p1)
文章目录 C 编程语言C 和 C 关系标准的 C 组成ANSI 标准比较重要的标准化时间 C 编程语言 是一种静态类型的、编译式的、通用式的、大小写敏感、不规则的编程语言支持过程化编程,面向对象,泛型编程 C 和 C 关系 C 是 C 的一个超集,任何合法…...

DRF之过滤,排序,分页
一、权限组件源码解读 1.继承了APIView 才有的---》执行流程---》dispatch中----》三大认证 APIView的dispatch def initial(self, request, *args, **kwargs):self.perform_authentication(request)self.check_permissions(request)self.check_throttles(request) 2 读…...

我的Redis学习,共写了14篇博客文章
早在19和20年全面学习SpringBoot相关技术知识时也曾经有学习到Redis,主要是看了几家的视频教程,但是未曾有具体的实践,后来再学习到Docker和Spring Session框架的Redis存储时,又稍微的实践了一丢丢,所有的实践也就仅此…...
mPython软件使用指南
①软件界面 一、软件界面的介绍 1.模式切换 硬件编程 Python3.6 Jupyter python3.6模式细节补充(一般不使用该模式,此处可跳过) Python3.6模式的界面 左侧指令分类栏 Python3.6模式的图形化指令分类分为: Python语法基础相关指令&…...

龙芯2K1000实战开发-系统配置详解
目录 概要 整体架构流程 技术名词解释 技术细节 编辑 总结...
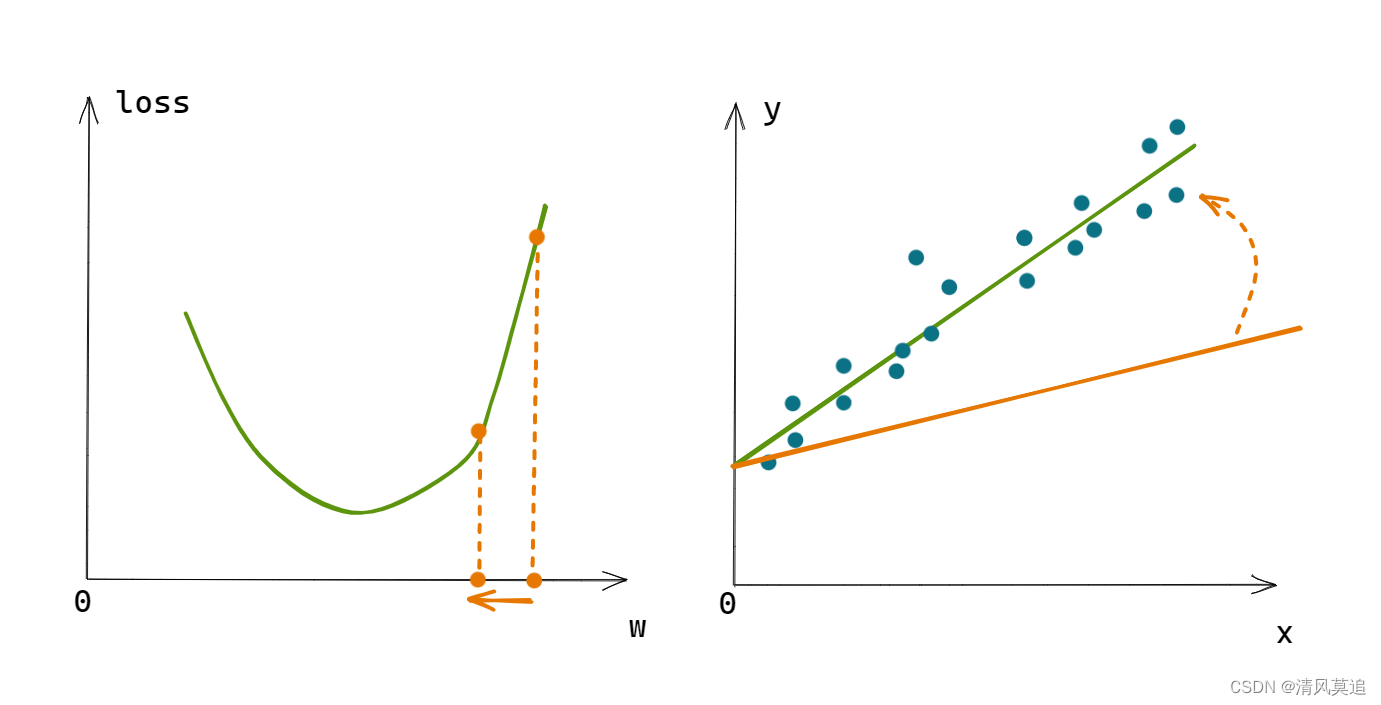
【一起撸个DL框架】5 实现:自适应线性单元
CSDN个人主页:清风莫追欢迎关注本专栏:《一起撸个DL框架》GitHub获取源码:https://github.com/flying-forever/OurDLblibli视频合集:https://space.bilibili.com/3493285974772098/channel/series 文章目录 5 实现:自适…...

开箱即用的工具函数库xijs更新指南(v1.2.6)
xijs 是一款开箱即用的 js 业务工具库, 聚集于解决业务中遇到的常用函数逻辑问题, 帮助开发者更高效的开展业务开发. 接下来就和大家一起分享一下 v1.2.6 版本的更新内容以及后续的更新方向. 贡献者列表: 1. 计算变量内存calculateMemory 该模块主要由 zhengsixsix 贡献, 我们可…...
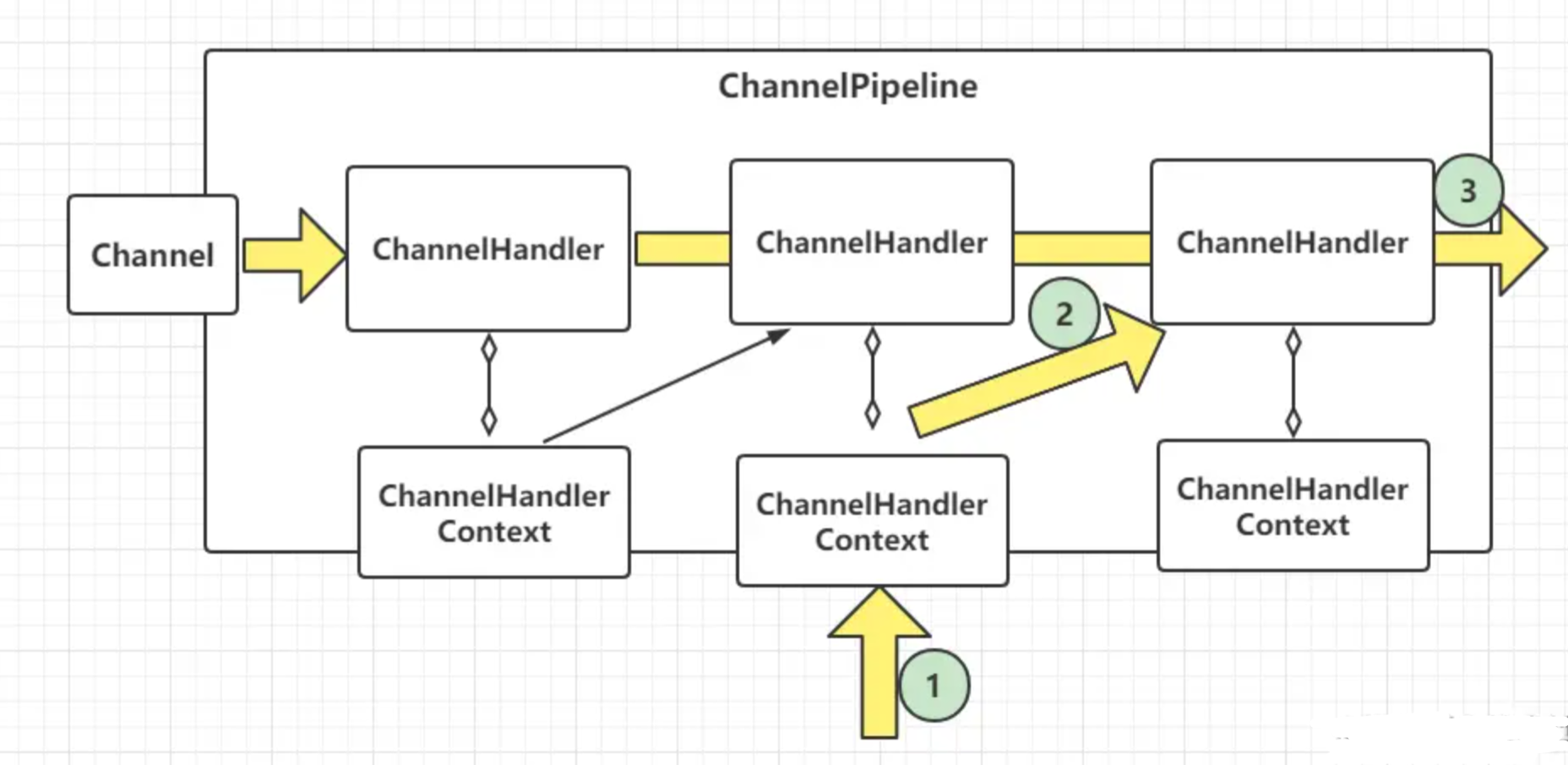
【Netty】ChannelPipeline源码分析(五)
文章目录 前言一、ChannelPipeline 接口1.1 创建 ChannelPipeline1.2 ChannelPipeline 事件传输机制1.2.1 处理出站事件1.2.2 处理入站事件 二、ChannelPipeline 中的 ChannelHandler三、ChannelHandlerContext 接口3.1 ChannelHandlerContext 与其他组件的关系3.2 跳过某些 Ch…...

并行计算技术解密:MPI和OpenMP的学习和应用指南
欢迎来到并行计算技术的奇妙世界!本指南将带您深入了解MPI(Message Passing Interface)和OpenMP(Open Multi-Processing)两种重要的并行计算技术,并为您提供学习和应用的指南。无论您是一个科研工作者、开发…...
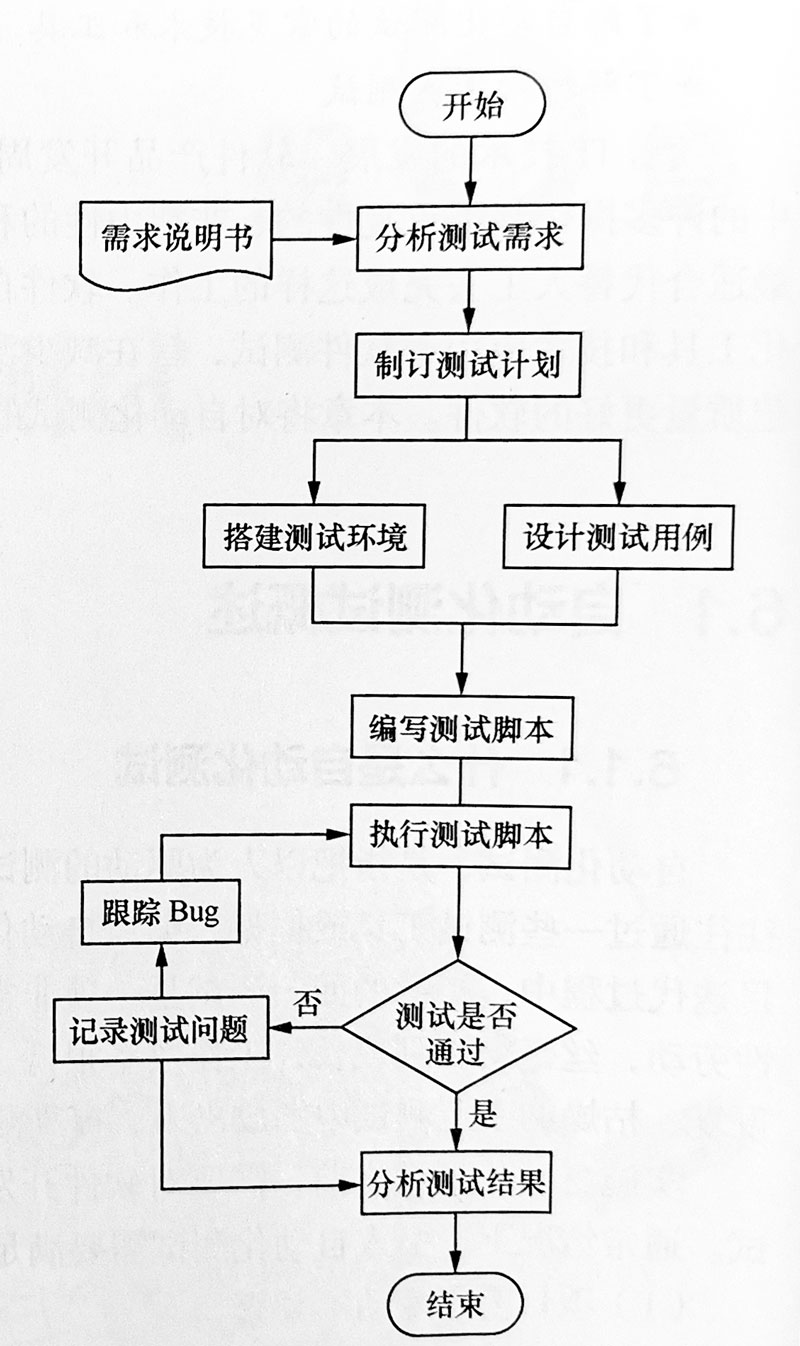
什么是自动化测试框架?我们该如何搭建自动化测试框架?
无论是在自动化测试实践,还是日常交流中,经常听到一个词:框架。之前学习自动化测试的过程中,一直对“框架”这个词知其然不知其所以然。 最近看了很多自动化相关的资料,加上自己的一些实践,算是对“框架”…...

Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics
Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that the same history topic isn‘t sha…...
javaWebssh中小学课件资源系统myeclipse开发mysql数据库MVC模式java编程计算机网页设计
一、源码特点 java ssh中小学课件资源系统是一套完善的web设计系统(系统采用ssh框架进行设计开发),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。开发环境为TOMCAT…...

MySQL高级查询操作
文章目录 前言聚集函数分组查询:GROUP BY过滤:HAVING嵌套子查询比较运算中使用子查询带有IN的子查询SOME(子查询)ALL(子查询)EXISTS子查询 前言 查询语句书写顺序: 1、select 2、from 3、where 4、group by 5、having 6、order by 7、limit …...
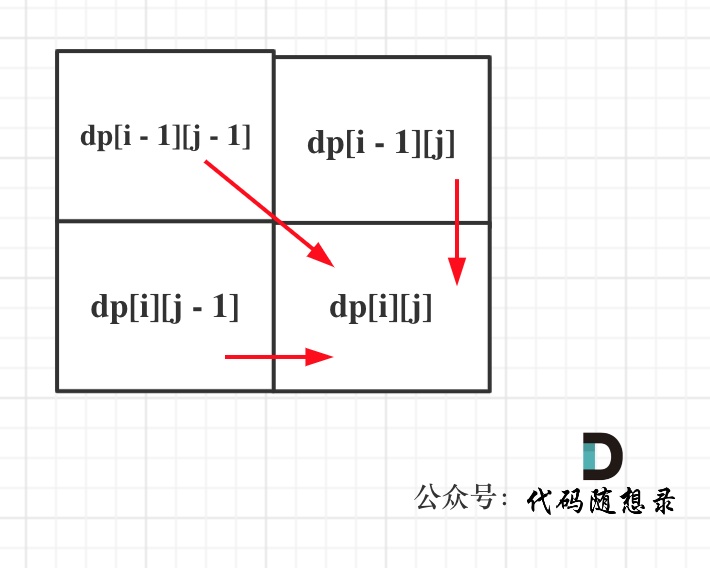
Day53【动态规划】1143.最长公共子序列、1035.不相交的线、53.最大子序和
1143.最长公共子序列 力扣题目链接/文章讲解 视频讲解 本题最大的难点还是定义 dp 数组 本题和718.最长重复子数组区别在于这里不要求是连续的了,但要有相对顺序 直接动态规划五部曲! 1、确定 dp 数组下标及值含义 dp[i][j]:取 text1…...

Three.js--》实现3d地球模型展示
目录 项目搭建 实现网页简单布局 初始化three.js基础代码 创建环境背景 加载地球模型 实现光柱效果 添加月球模型 今天简单实现一个three.js的小Demo,加强自己对three知识的掌握与学习,只有在项目中才能灵活将所学知识运用起来,话不多…...
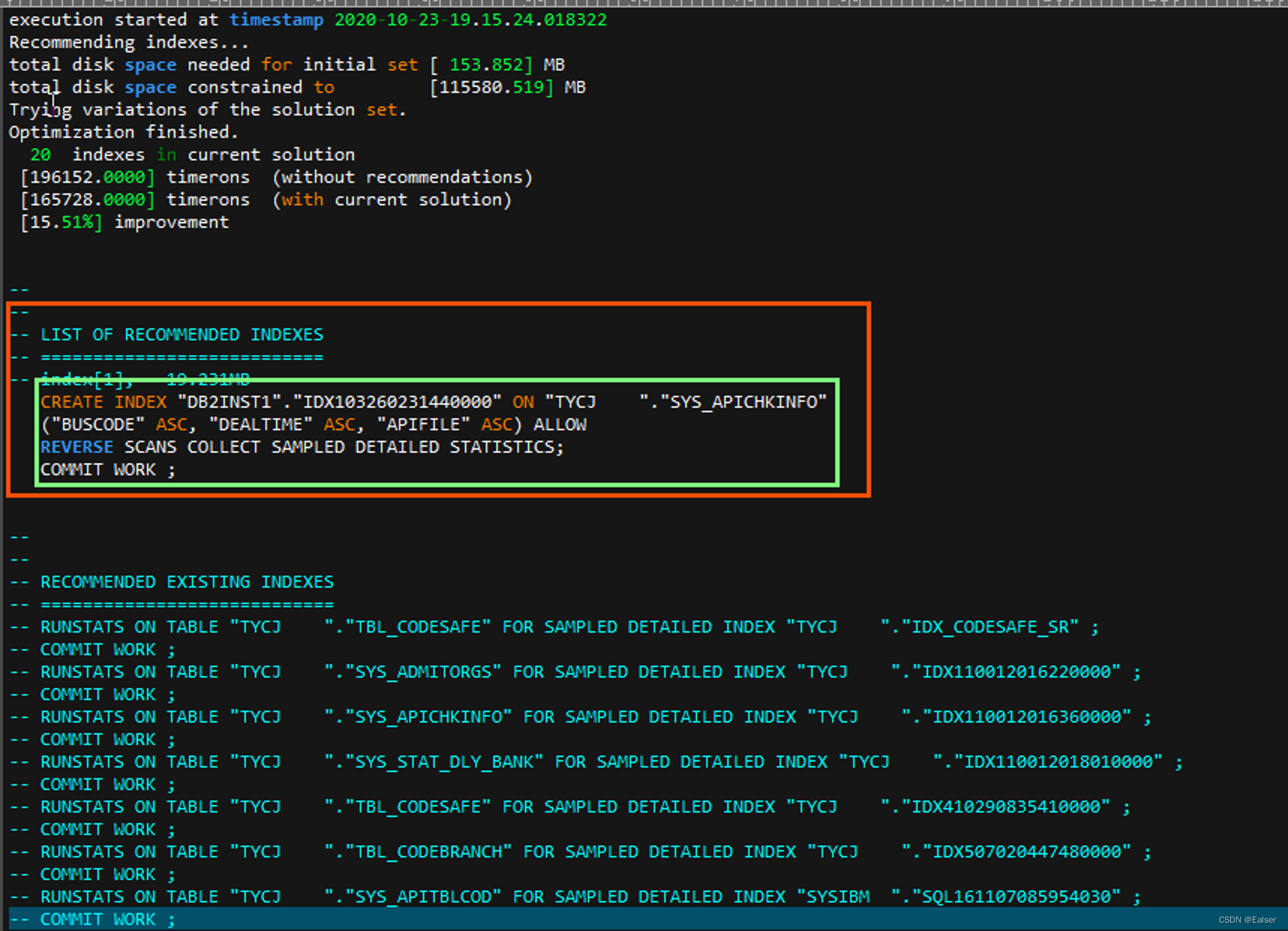
<SQL>《SQL命令(含例句)精心整理版(6)》
《SQL命令(含例句)精心整理版(6)》 18 DB2查询语句18.1 查询数据库大小18.2 查看表占表空间大小18.3 查看正在执行的语句18.4 db2expln 查看执行计划18.5 db2advis 查看优化建议 19 空值19.1 NULL19.2 TRIM 18 DB2查询语句 18.1 …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
