对KMP算法的一点碎碎念——上篇
对KMP算法的一点碎碎念——上篇
文章目录
- 对KMP算法的一点碎碎念——上篇
- 1. KMP 算法 Next数组 求解问题
- 1.1 前置知识-最长公共前后缀LCP
- 1.1.1 前缀与后缀
- 1.1.2 最长公共前后缀LCP
- 1.2 手算法求解 Next数组值(3种常见情况)
- 1.2.1 情况1: next数组 正常存放匹配字符的长度
- 情况1的失配回溯机制
- 1.2.2 情况2: next数组 整体右移一位
- 情况2的失配回溯机制
- 1.2.3 情况3: next数组 整体右移一位并把next数组加1
- 情况3的失配回溯机制
- 参考资料
1. KMP 算法 Next数组 求解问题
假设有模式串T为:a b a b a c,求解与其对应的next数组为多少
1.1 前置知识-最长公共前后缀LCP
1.1.1 前缀与后缀
前缀的概念:前缀是 不包含最后一个字符 的所有 以第一个字符开头 的任意子串
后缀的概念:后缀是 不包含第一个字符 的所有 以最后一个字符结尾 的任意子串
例如字符串 “aba”
-
去掉最后一个字符后,剩下的都是前缀了
a b a ab\xcancel{a} aba ,这里 ab 就是这个字符串的其中一个前缀
-
同理去掉第一个字符后,剩下的都是后缀了
a b a \xcancel{a}ba a ba,这里 ba 就是这个字符串的其中一个后缀
为什么这里我说是其中一个前/后缀呢?
回到前后缀的概念上,前后缀都是以子串的形式存在的,也就是说,前后缀一定是模式串的子集
那么就好理解了,aba的前后缀表如下:
| 前缀 | 后缀 |
|---|---|
| a | a |
| ab | ba |
1.1.2 最长公共前后缀LCP
概念:最长公共前后缀 (longest common prefix) 就是字符串中前缀和后缀的 最长匹配子串
例如,“aabaa”,我们从 前缀(prefix)和后缀(suffix) 中寻找最长的匹配子串
| 字符串 aabaa 的子串 | 前缀(去掉最后一个字符) | 被去掉的字符 | 后缀(去掉第一个字符) | 被去掉的字符 | 前后缀最长匹配数(就是next值) |
|---|---|---|---|---|---|
| a | ✗ | a \xcancel{a} a | ✗ | a \xcancel{a} a | 0 |
| aa | a | a a a\xcancel{a} aa | a | a a \xcancel{a}a a a | 1 |
| aab | a, aa | a a b aa\xcancel{b} aab | b, ab | a a b \xcancel{a}ab a ab | 0 |
| aaba | a, aa, aab | a a b a aab\xcancel{a} aaba | a, ba, aba | a a b a \xcancel{a}aba a aba | 1 |
| aabaa | a, aa, aab, aaba | a a b a a aaba\xcancel{a} aabaa | a, aa, baa, abaa | a a b a a \xcancel{a}abaa a abaa | 2 |
1.2 手算法求解 Next数组值(3种常见情况)
由于KMP算法中的next数组有不同的实现方式,因此为了避免大家弄混淆,我对每个实现next数组的方法做一些区分
1.2.1 情况1: next数组 正常存放匹配字符的长度
这是最常见的情况,基本上网络上大部分都是以这个情况为主来求解next数组值,我们上面也讨论过了next值如何得出
以模式串 “ababac” 为例,完整的next数组如下:
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 模式串 | a | b | a | b | a | c |
| next数组值 | 0 | 0 | 1 | 2 | 3 | 0 |
| 匹配的前后缀 | ✗ | ✗ | a b a 匹配位为前后缀 ‘a’ | a b a b 匹配位为前后缀 ‘a b’ | a b a b a 匹配位为前后缀 ‘a b a’ | ✗ |
我们可以发现,每个字符下的next数组值都是存放着当前串的匹配长度
初学者可能会对第4个位置有疑惑,咱们一起来看如何求解?
模式串匹配到第4个字符后,前4个字符组成了一个串,即"ababa"
前缀的集合为: a , a b , a b a , a b a b a,ab,aba,abab a,ab,aba,abab
后缀的集合为: a , b a , a b a , b a b a a,ba,aba,baba a,ba,aba,baba
通过观察,我们可以看到集合中 a b a aba aba 为最长公共前后缀,且长度为3
情况1的失配回溯机制
假如文本串(主串)为 “abababac”,模式串为 “ababac”,在下标为5的位置发生失配
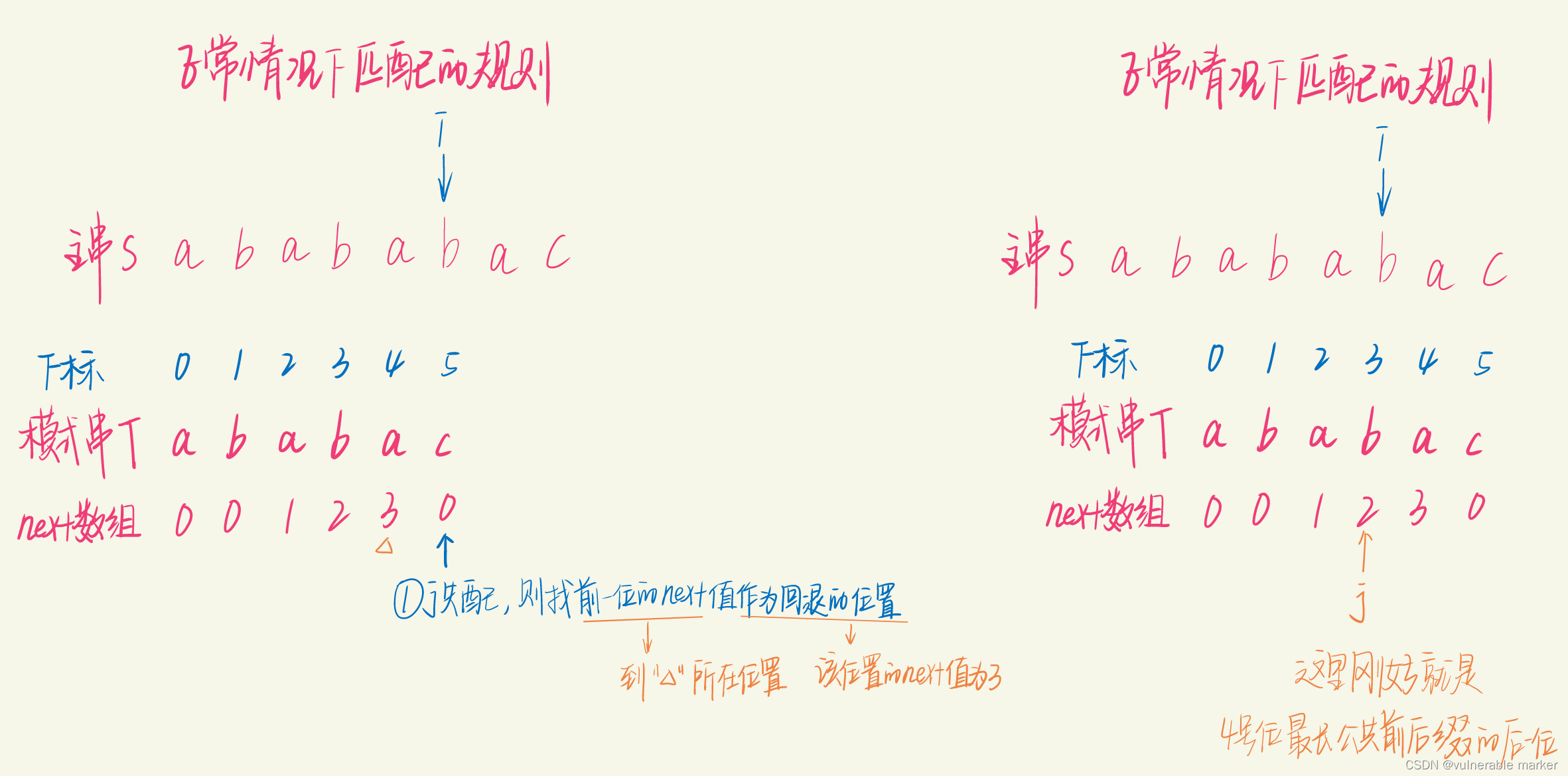
从图中我们看出:
-
左侧图,当主串S和模式串T比较到下标为5的位置时,发现主串和模式串不匹配,故模式串的指针j需要回退,回退的顺序为
-
寻找找从当前失配位置的前一位,它的next值是多少?
当前失配位置为下标5,它前一位的next值为3
-
前一位的next值就是j要回退的位置的下标
那么j要回退的位置就是 j = next[j-1] = next[4] = 3
-
-
右侧图,我们已经找到回退的位置了,故j回到下标为3的位置上继续与主串S重新匹配
还有一种的实现方式是和这个原理一样的,就是把这所有的next数组值减1,然后找回溯位置时再把next值加1而已
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 模式串 | a | b | a | b | a | c |
| next数组值 | -1 | -1 | 0 | 1 | 2 | -1 |
回溯位:j = next[j-1] + 1
不难看出,虽然好理解,但是操作很繁琐。每一次j失配都需要找前一位的next值作为自己的回退位置,这时候有人对next数组做出了改进,当在当前位置失配时,直接获取当前失配位置的next值作为j回退的位置,这就是我们要讲解的下一种情况
1.2.2 情况2: next数组 整体右移一位
以模式串 “ababac” 为例,完整的next数组如下:
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 模式串 | a | b | a | b | a | c |
| next数组值 | -1 | 0 | 0 | 1 | 2 | 3 |
| 匹配的前后缀 | ✗ | ✗ | ✗ | a b a 匹配位为前后缀 ‘a’ | a b a b 匹配位为前后缀 ‘a b’ | a b a b a 匹配位为前后缀 ‘a b a’ |
你可能会疑惑,这样做也没什么区别啊,反而更难理解了?实则不然,我们看下面的比较方式就能看出来了

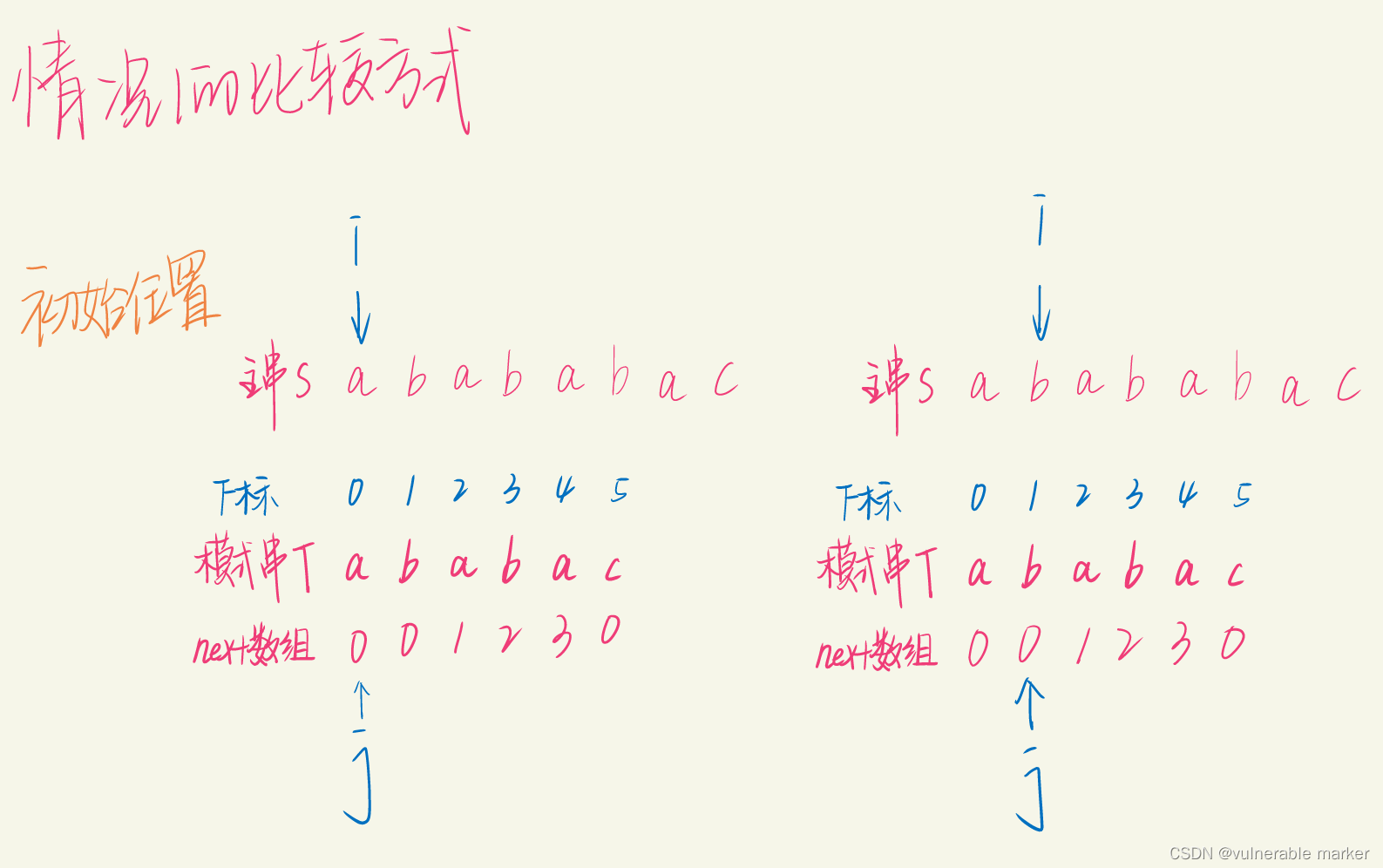
字符串匹配最本质的原理其实就是前后缀相匹配的问题,我们把模式串右移一位,在逻辑上更符合匹配的情况,这就是为什么大部分教程和书籍都用这两种方式讲解next数组值的原因。那么,除了逻辑上更符合之外,还有next数组右移一位还有什么优势呢?我们再看下面的图解
情况2的失配回溯机制
假如文本串(主串)为 “abababac”,模式串为 “ababac”,使用右移模式串T的方式与主串S进行匹配
当前位置不匹配,那么就直接从不匹配的位置获取next数组值,然后j就回退到当前位置的next对应的下标位置。对齐的那个地方不算一个步骤,只是为了让大家更好理解


通过以上图片对比,我们发现把next数组整体右移一位在一定情况下的匹配效率更高,这就是为什么右移next数组这么流行的原因了
回溯位:j = next[j]
1.2.3 情况3: next数组 整体右移一位并把next数组加1
以模式串 “ababac” 为例,完整的next数组如下:
| 模式串下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 模式串 | ✗ | a | b | a | b | a | c |
| next数组值 | ✗ | 0 | 1 | 1 | 2 | 3 | 4 |
| 匹配的前后缀 | ✗ | ✗ | ✗ | ✗ | a b a 匹配位为前后缀 ‘a’ | a b a b 匹配位为前后缀 ‘a b’ | a b a b a 匹配位为前后缀 ‘a b a’ |
其实情况3的实现方式和情况2是一样的,只不过我们发现情况3的next数组的初始位置是从1开始,而情况1的next数组的初始位置是从0开始的
不过我个人认为,情况3更像是情况1和情况2的结合,它杂糅了它们的思想,为什么这么说?先给出结论
-
在回溯机制上,情况3的回溯机制思想和情况2的回溯机制思想是一样的
都是当前位置不匹配,那么就直接从不匹配的位置获取next数组值,然后j就回退到当前位置的next对应的下标位置
情况3的回溯机制也就是 j = next[j] 而不是情况1的 j = next[j-1] -
在next数组值确定上,情况3的数组值确定方式和情况1是一样的
都是从当前位置及之前构成的串中寻找 最长公共前后缀,然后把匹配的值确定为当前位置的next值
情况3的失配回溯机制
假如文本串(主串)为 “abababac”,模式串为 “ababac”,使用右移模式串T并把下标加1的方式与主串S进行匹配
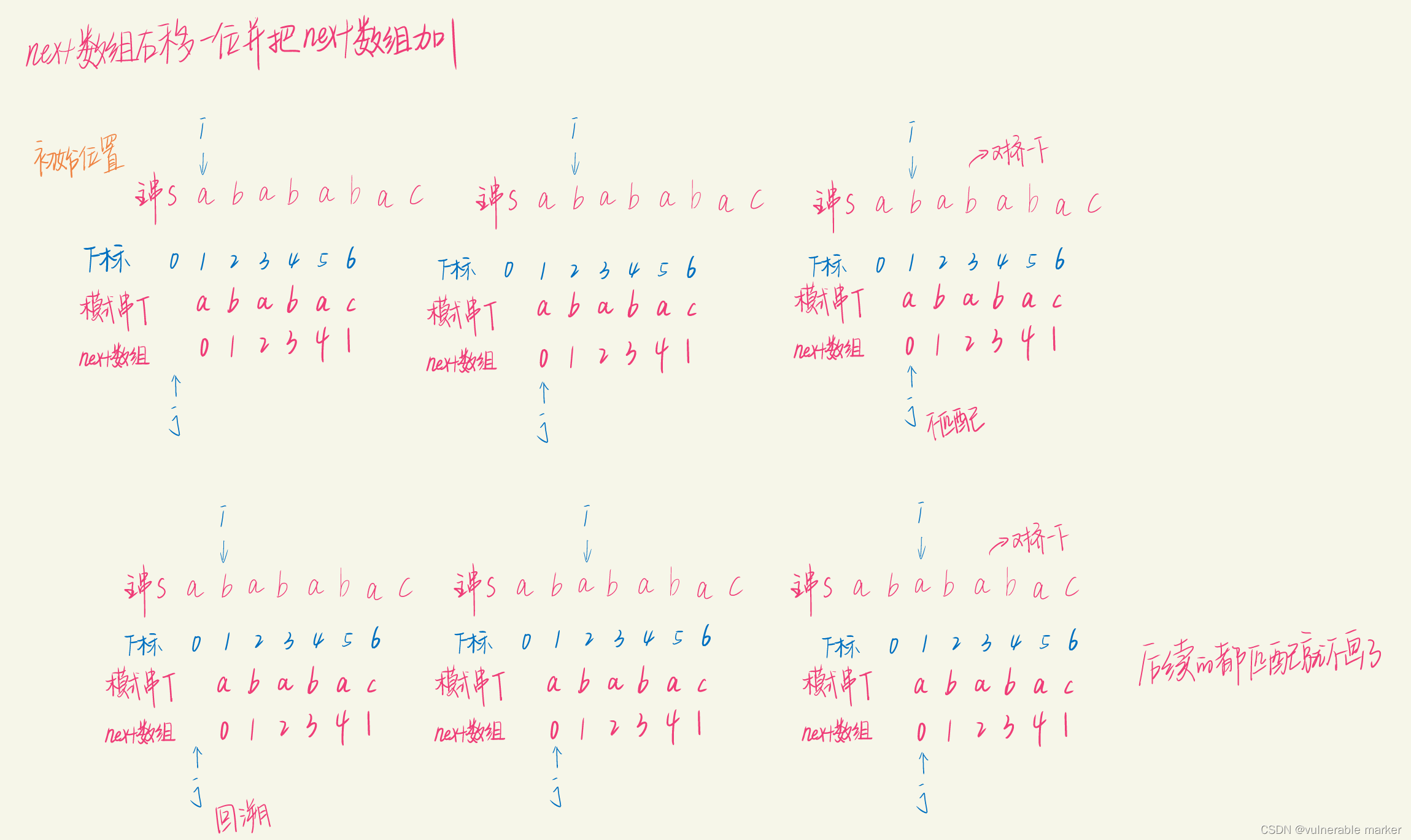
回溯位:j = next[j]
参考资料
KMP算法之求解next数组 (xiaohongshu.com)
帮你把 KMP 算法学个通透!(理论篇)
帮你把KMP算法学个通透!(求next数组代码篇)
KMP 算法之求next数组代码讲解
KMP算法精讲(1)——暴力匹配算法
KMP算法精讲(2)——什么是最长公共前后缀?
KMP算法精讲(3)——最长公共前后缀在KMP算法中的应用
KMP算法精讲(4)——15分钟搞定next数组
KMP Algorithm for Pattern Searching - GeeksforGeeks
Prefix function - Knuth-Morris-Pratt Algorithm - Coding Ninjas
相关文章:

对KMP算法的一点碎碎念——上篇
对KMP算法的一点碎碎念——上篇 文章目录 对KMP算法的一点碎碎念——上篇1. KMP 算法 Next数组 求解问题1.1 前置知识-最长公共前后缀LCP1.1.1 前缀与后缀1.1.2 最长公共前后缀LCP 1.2 手算法求解 Next数组值(3种常见情况)1.2.1 情况1: next数组 正常存放匹配字符的长度情况1的…...

算法---边界着色
题目 给你一个大小为 m x n 的整数矩阵 grid ,表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。 两个网格块属于同一 连通分量 需满足下述全部条件: 两个网格块颜色相同 在上、下、左、右任意一个方向上…...

二叉排序树的查找、插入、删除
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的定义 二叉排序树的定义 二叉排序树(Binary Sort Tree, BST),也称二叉查找树。 二叉排序树或者是一棵空树,或者是一棵具有下列特性的非空二叉…...
《Opencv3编程入门》学习笔记—第三章
《Opencv3编程入门》学习笔记 记录一下在学习《Opencv3编程入门》这本书时遇到的问题或重要的知识点。 第三章 HighGUI图形用户界面初步 一、图像的载入、显示和输出到文件 (一)OpenCV的命名空间 简单的OpenCV程序标配: #include <o…...
如何从Ubuntu Linux中删除Firefox Snap?
Ubuntu Linux是一款广受欢迎的开源操作系统,拥有强大的功能和广泛的应用程序选择。默认情况下,Ubuntu提供了一种称为Snap的软件打包格式,用于安装和管理应用程序。Firefox是一款流行的开源网络浏览器,而Firefox Snap是Firefox的Sn…...
数学建模的初阶-快速上手
目录 第一步:明确问题 第二步:选择建模方法 第三步:收集数据 第四步:构建数学模型 第五步:模型验证与评估 数学建模软件推荐 统计模型 (1) 线性回归模型 (2) 逻辑回归模型 (3) 时间序列模型 优化模型 (1) …...
)
复习向 C/C++ 编程语言简介和概括(C++复习向p1)
文章目录 C 编程语言C 和 C 关系标准的 C 组成ANSI 标准比较重要的标准化时间 C 编程语言 是一种静态类型的、编译式的、通用式的、大小写敏感、不规则的编程语言支持过程化编程,面向对象,泛型编程 C 和 C 关系 C 是 C 的一个超集,任何合法…...

DRF之过滤,排序,分页
一、权限组件源码解读 1.继承了APIView 才有的---》执行流程---》dispatch中----》三大认证 APIView的dispatch def initial(self, request, *args, **kwargs):self.perform_authentication(request)self.check_permissions(request)self.check_throttles(request) 2 读…...

我的Redis学习,共写了14篇博客文章
早在19和20年全面学习SpringBoot相关技术知识时也曾经有学习到Redis,主要是看了几家的视频教程,但是未曾有具体的实践,后来再学习到Docker和Spring Session框架的Redis存储时,又稍微的实践了一丢丢,所有的实践也就仅此…...
mPython软件使用指南
①软件界面 一、软件界面的介绍 1.模式切换 硬件编程 Python3.6 Jupyter python3.6模式细节补充(一般不使用该模式,此处可跳过) Python3.6模式的界面 左侧指令分类栏 Python3.6模式的图形化指令分类分为: Python语法基础相关指令&…...

龙芯2K1000实战开发-系统配置详解
目录 概要 整体架构流程 技术名词解释 技术细节 编辑 总结...
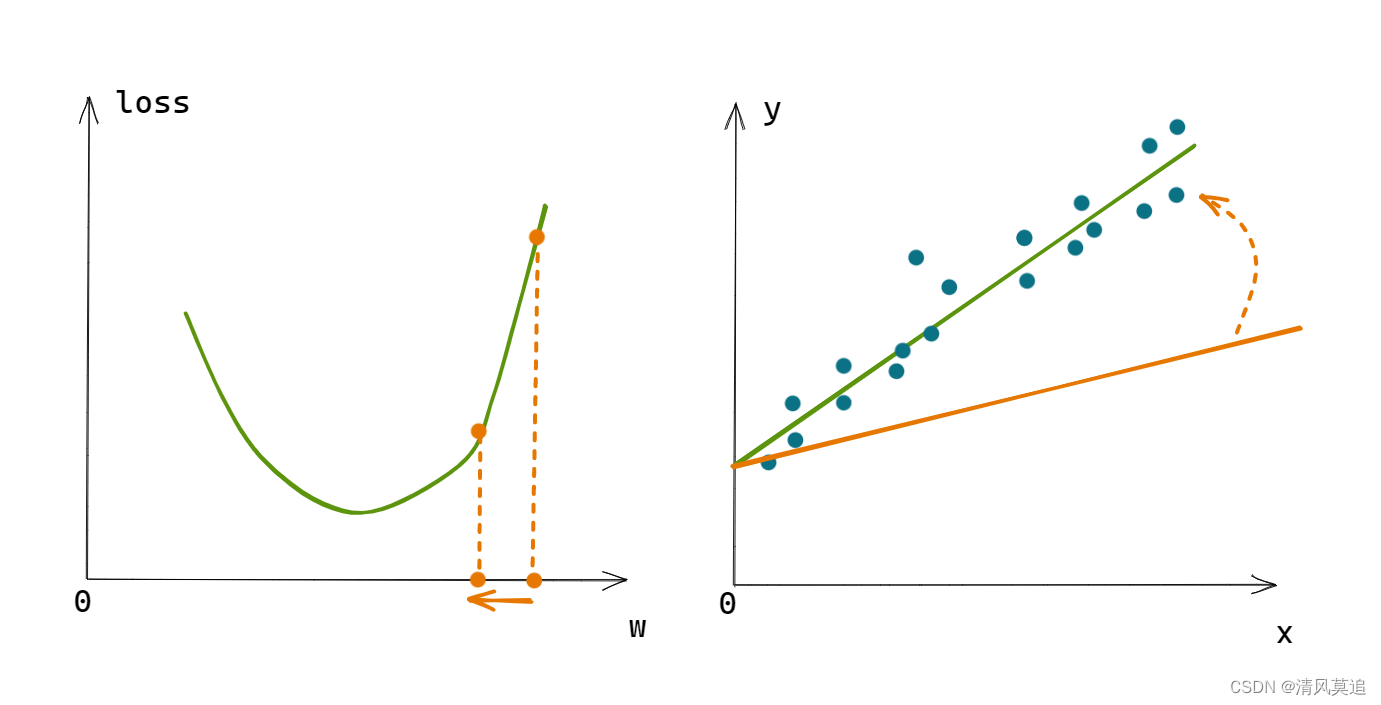
【一起撸个DL框架】5 实现:自适应线性单元
CSDN个人主页:清风莫追欢迎关注本专栏:《一起撸个DL框架》GitHub获取源码:https://github.com/flying-forever/OurDLblibli视频合集:https://space.bilibili.com/3493285974772098/channel/series 文章目录 5 实现:自适…...

开箱即用的工具函数库xijs更新指南(v1.2.6)
xijs 是一款开箱即用的 js 业务工具库, 聚集于解决业务中遇到的常用函数逻辑问题, 帮助开发者更高效的开展业务开发. 接下来就和大家一起分享一下 v1.2.6 版本的更新内容以及后续的更新方向. 贡献者列表: 1. 计算变量内存calculateMemory 该模块主要由 zhengsixsix 贡献, 我们可…...
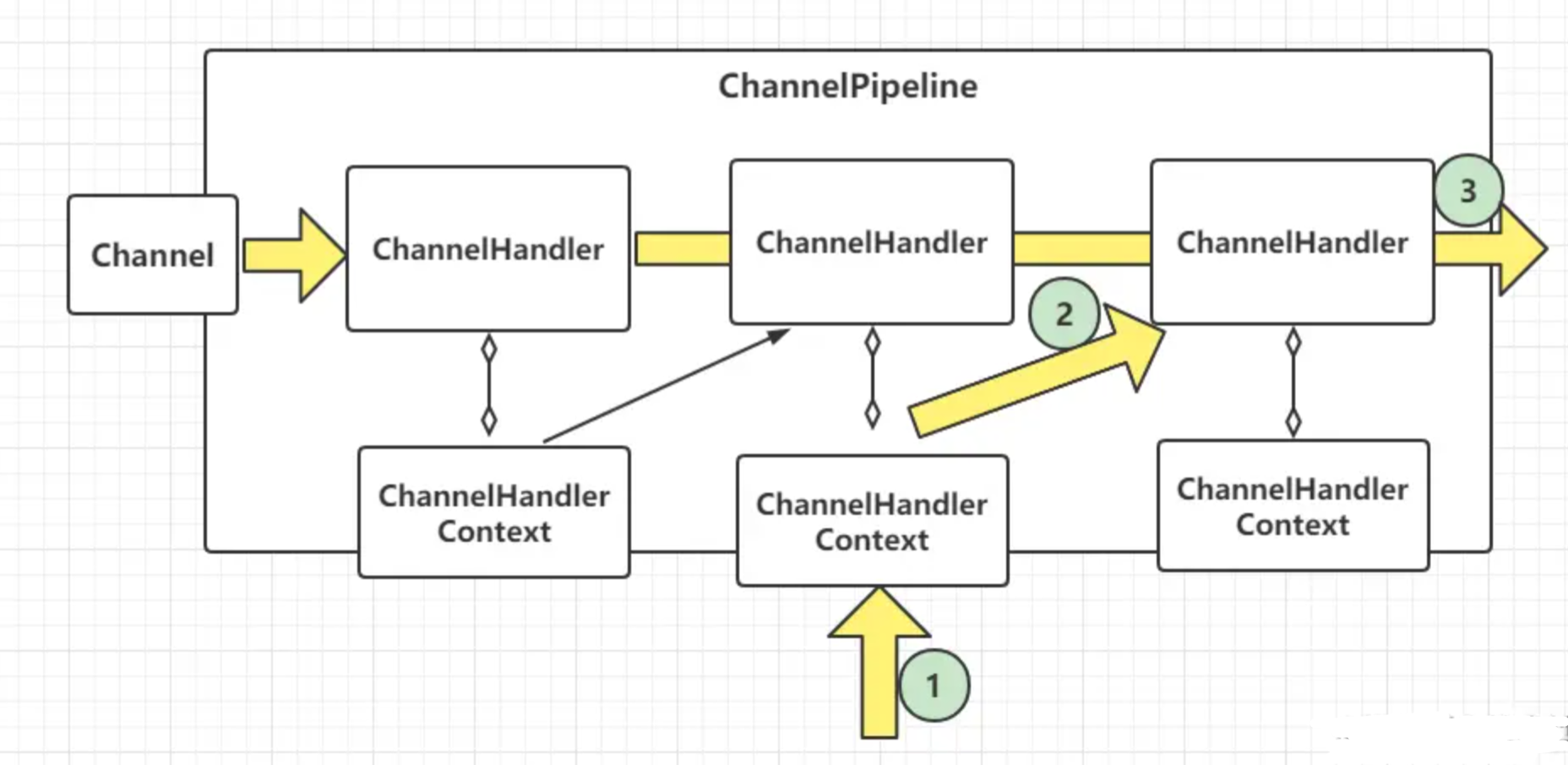
【Netty】ChannelPipeline源码分析(五)
文章目录 前言一、ChannelPipeline 接口1.1 创建 ChannelPipeline1.2 ChannelPipeline 事件传输机制1.2.1 处理出站事件1.2.2 处理入站事件 二、ChannelPipeline 中的 ChannelHandler三、ChannelHandlerContext 接口3.1 ChannelHandlerContext 与其他组件的关系3.2 跳过某些 Ch…...

并行计算技术解密:MPI和OpenMP的学习和应用指南
欢迎来到并行计算技术的奇妙世界!本指南将带您深入了解MPI(Message Passing Interface)和OpenMP(Open Multi-Processing)两种重要的并行计算技术,并为您提供学习和应用的指南。无论您是一个科研工作者、开发…...
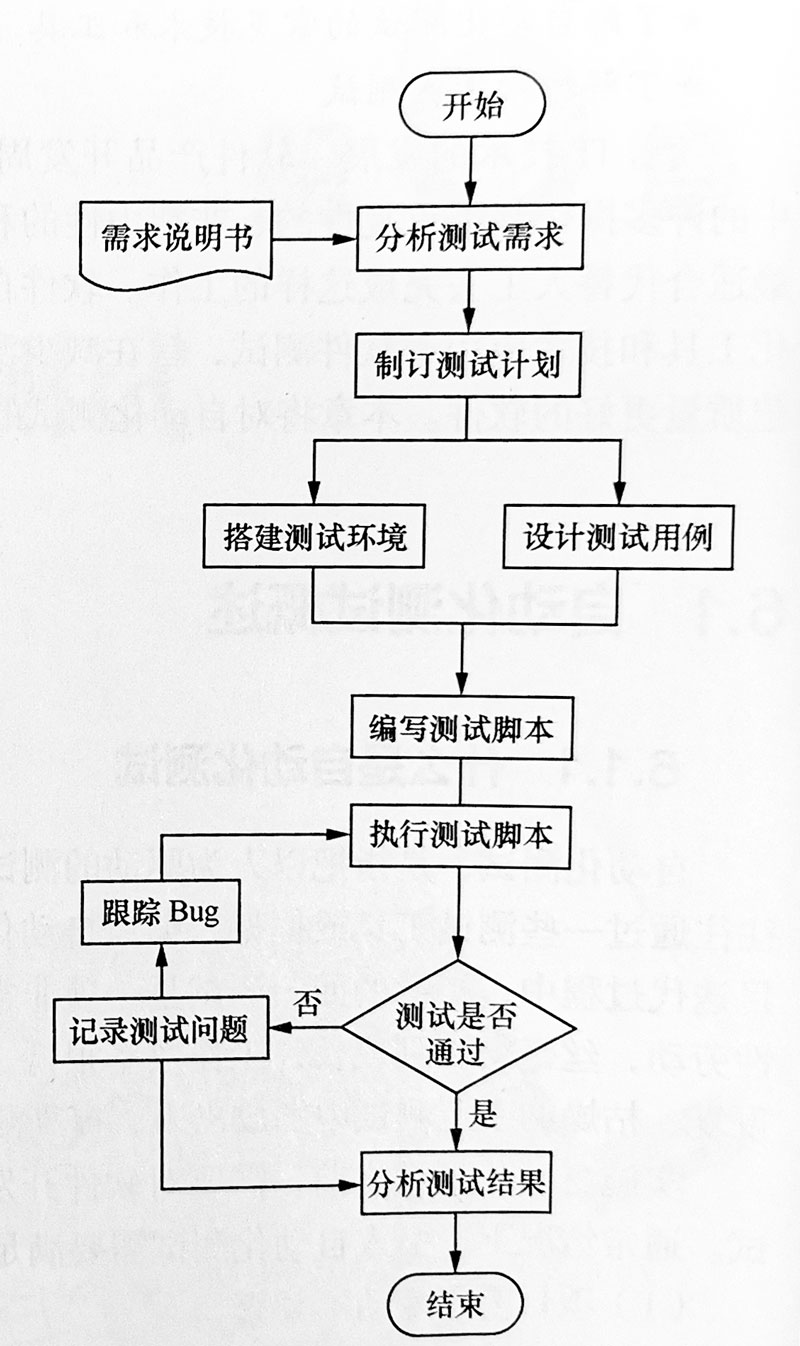
什么是自动化测试框架?我们该如何搭建自动化测试框架?
无论是在自动化测试实践,还是日常交流中,经常听到一个词:框架。之前学习自动化测试的过程中,一直对“框架”这个词知其然不知其所以然。 最近看了很多自动化相关的资料,加上自己的一些实践,算是对“框架”…...

Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics
Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that the same history topic isn‘t sha…...
javaWebssh中小学课件资源系统myeclipse开发mysql数据库MVC模式java编程计算机网页设计
一、源码特点 java ssh中小学课件资源系统是一套完善的web设计系统(系统采用ssh框架进行设计开发),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。开发环境为TOMCAT…...

MySQL高级查询操作
文章目录 前言聚集函数分组查询:GROUP BY过滤:HAVING嵌套子查询比较运算中使用子查询带有IN的子查询SOME(子查询)ALL(子查询)EXISTS子查询 前言 查询语句书写顺序: 1、select 2、from 3、where 4、group by 5、having 6、order by 7、limit …...
Day53【动态规划】1143.最长公共子序列、1035.不相交的线、53.最大子序和
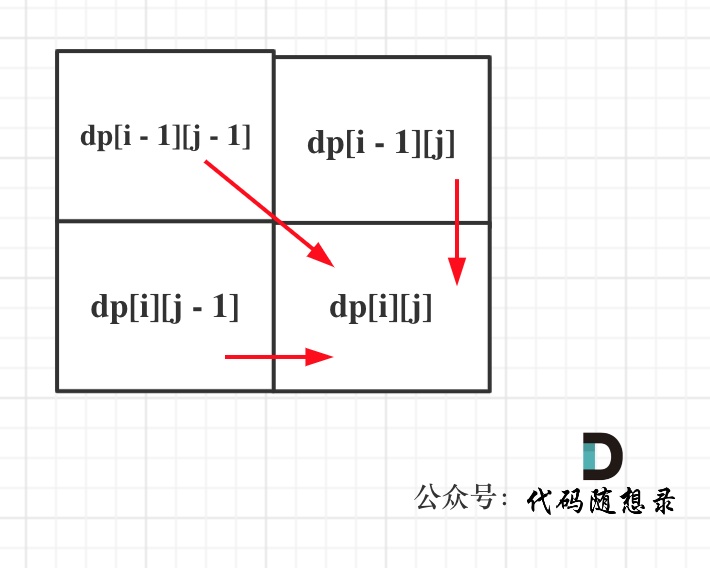
1143.最长公共子序列 力扣题目链接/文章讲解 视频讲解 本题最大的难点还是定义 dp 数组 本题和718.最长重复子数组区别在于这里不要求是连续的了,但要有相对顺序 直接动态规划五部曲! 1、确定 dp 数组下标及值含义 dp[i][j]:取 text1…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
