算法---边界着色
题目
给你一个大小为 m x n 的整数矩阵 grid ,表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。
两个网格块属于同一 连通分量 需满足下述全部条件:
两个网格块颜色相同
在上、下、左、右任意一个方向上相邻
连通分量的边界 是指连通分量中满足下述条件之一的所有网格块:
在上、下、左、右任意一个方向上与不属于同一连通分量的网格块相邻
在网格的边界上(第一行/列或最后一行/列)
请你使用指定颜色 color 为所有包含网格块 grid[row][col] 的 连通分量的边界 进行着色,并返回最终的网格 grid 。
示例 1:
输入:grid = [[1,1],[1,2]], row = 0, col = 0, color = 3
输出:[[3,3],[3,2]]
示例 2:
输入:grid = [[1,2,2],[2,3,2]], row = 0, col = 1, color = 3
输出:[[1,3,3],[2,3,3]]
示例 3:
输入:grid = [[1,1,1],[1,1,1],[1,1,1]], row = 1, col = 1, color = 2
输出:[[2,2,2],[2,1,2],[2,2,2]]
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j], color <= 1000
0 <= row < m
0 <= col < n
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/coloring-a-border
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解决方法
//一定要注意是边界fun colorBorder(grid: Array<IntArray>, row: Int, col: Int, color: Int): Array<IntArray> {//简单粗暴 直接按照思路走//题意有点难懂 边界 val dp = Array(grid.size) {BooleanArray(grid[0].size) { false }}//注意这里需要对二维数组 进行深copyval copyOf = grid.map { t -> t.copyOf() }.toTypedArray()dfs(grid, grid[row][col], color, row, col, dp,copyOf)return grid}fun dfs(grid: Array<IntArray>, old: Int, new: Int, row: Int, col: Int, dp: Array<BooleanArray>, origin: Array<IntArray>) {if (row in grid.indices && col in grid[0].indices && origin[row][col] == old && !dp[row][col]) {dp[row][col] = trueif (row == 0 || row == grid.size - 1 || col == 0 || col == grid[0].size - 1 || board(origin,row,col)) {grid[row][col] = new}dfs(grid, old, new, row + 1, col, dp,origin)dfs(grid, old, new, row, col + 1, dp,origin)dfs(grid, old, new, row - 1, col, dp,origin)dfs(grid, old, new, row, col - 1, dp,origin)}}fun board(grid: Array<IntArray>, row: Int, col: Int) : Boolean{if (row in grid.indices && col in grid[0].indices){if (grid[row + 1][col] != grid[row][col] ||grid[row - 1][col] != grid[row][col] ||grid[row ][col + 1] != grid[row][col] ||grid[row ][col - 1] != grid[row][col]){return true}}return false}
总结
1.既生瑜 何生亮
最近在看三国 几年前我也看过几次 但是从来都是看不到多少章就不看了
现在有二周了 看了上半部分了
感觉有些书。不到一些年纪就是读不进去
而且有些精彩的部分 看不懂 但是也不影响看懂的部分的精彩
读取一遍能够全部吸收。我觉得至少我认识的人中没有人能做到
长篇小说就是需要耐心、不可急躁
年轻就是容易急躁
也不懂的欣赏一些作品
现在我学会去以欣赏的角度问自己:
为什么三国可以成为经典?一定有他精彩的地方
这个精彩的地方我不想别人告诉我
我想自己去看看
相关文章:

算法---边界着色
题目 给你一个大小为 m x n 的整数矩阵 grid ,表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。 两个网格块属于同一 连通分量 需满足下述全部条件: 两个网格块颜色相同 在上、下、左、右任意一个方向上…...

二叉排序树的查找、插入、删除
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的定义 二叉排序树的定义 二叉排序树(Binary Sort Tree, BST),也称二叉查找树。 二叉排序树或者是一棵空树,或者是一棵具有下列特性的非空二叉…...
《Opencv3编程入门》学习笔记—第三章
《Opencv3编程入门》学习笔记 记录一下在学习《Opencv3编程入门》这本书时遇到的问题或重要的知识点。 第三章 HighGUI图形用户界面初步 一、图像的载入、显示和输出到文件 (一)OpenCV的命名空间 简单的OpenCV程序标配: #include <o…...
如何从Ubuntu Linux中删除Firefox Snap?
Ubuntu Linux是一款广受欢迎的开源操作系统,拥有强大的功能和广泛的应用程序选择。默认情况下,Ubuntu提供了一种称为Snap的软件打包格式,用于安装和管理应用程序。Firefox是一款流行的开源网络浏览器,而Firefox Snap是Firefox的Sn…...
数学建模的初阶-快速上手
目录 第一步:明确问题 第二步:选择建模方法 第三步:收集数据 第四步:构建数学模型 第五步:模型验证与评估 数学建模软件推荐 统计模型 (1) 线性回归模型 (2) 逻辑回归模型 (3) 时间序列模型 优化模型 (1) …...
)
复习向 C/C++ 编程语言简介和概括(C++复习向p1)
文章目录 C 编程语言C 和 C 关系标准的 C 组成ANSI 标准比较重要的标准化时间 C 编程语言 是一种静态类型的、编译式的、通用式的、大小写敏感、不规则的编程语言支持过程化编程,面向对象,泛型编程 C 和 C 关系 C 是 C 的一个超集,任何合法…...

DRF之过滤,排序,分页
一、权限组件源码解读 1.继承了APIView 才有的---》执行流程---》dispatch中----》三大认证 APIView的dispatch def initial(self, request, *args, **kwargs):self.perform_authentication(request)self.check_permissions(request)self.check_throttles(request) 2 读…...

我的Redis学习,共写了14篇博客文章
早在19和20年全面学习SpringBoot相关技术知识时也曾经有学习到Redis,主要是看了几家的视频教程,但是未曾有具体的实践,后来再学习到Docker和Spring Session框架的Redis存储时,又稍微的实践了一丢丢,所有的实践也就仅此…...
mPython软件使用指南
①软件界面 一、软件界面的介绍 1.模式切换 硬件编程 Python3.6 Jupyter python3.6模式细节补充(一般不使用该模式,此处可跳过) Python3.6模式的界面 左侧指令分类栏 Python3.6模式的图形化指令分类分为: Python语法基础相关指令&…...

龙芯2K1000实战开发-系统配置详解
目录 概要 整体架构流程 技术名词解释 技术细节 编辑 总结...
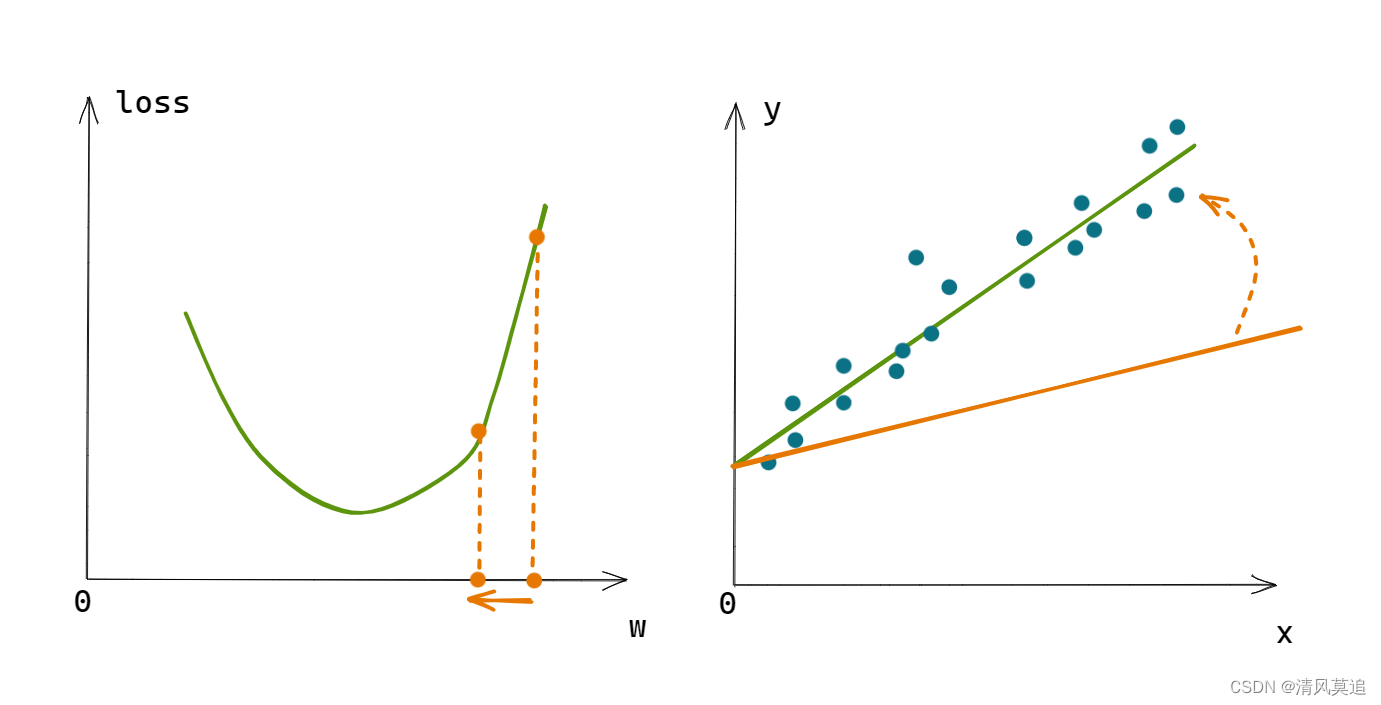
【一起撸个DL框架】5 实现:自适应线性单元
CSDN个人主页:清风莫追欢迎关注本专栏:《一起撸个DL框架》GitHub获取源码:https://github.com/flying-forever/OurDLblibli视频合集:https://space.bilibili.com/3493285974772098/channel/series 文章目录 5 实现:自适…...

开箱即用的工具函数库xijs更新指南(v1.2.6)
xijs 是一款开箱即用的 js 业务工具库, 聚集于解决业务中遇到的常用函数逻辑问题, 帮助开发者更高效的开展业务开发. 接下来就和大家一起分享一下 v1.2.6 版本的更新内容以及后续的更新方向. 贡献者列表: 1. 计算变量内存calculateMemory 该模块主要由 zhengsixsix 贡献, 我们可…...
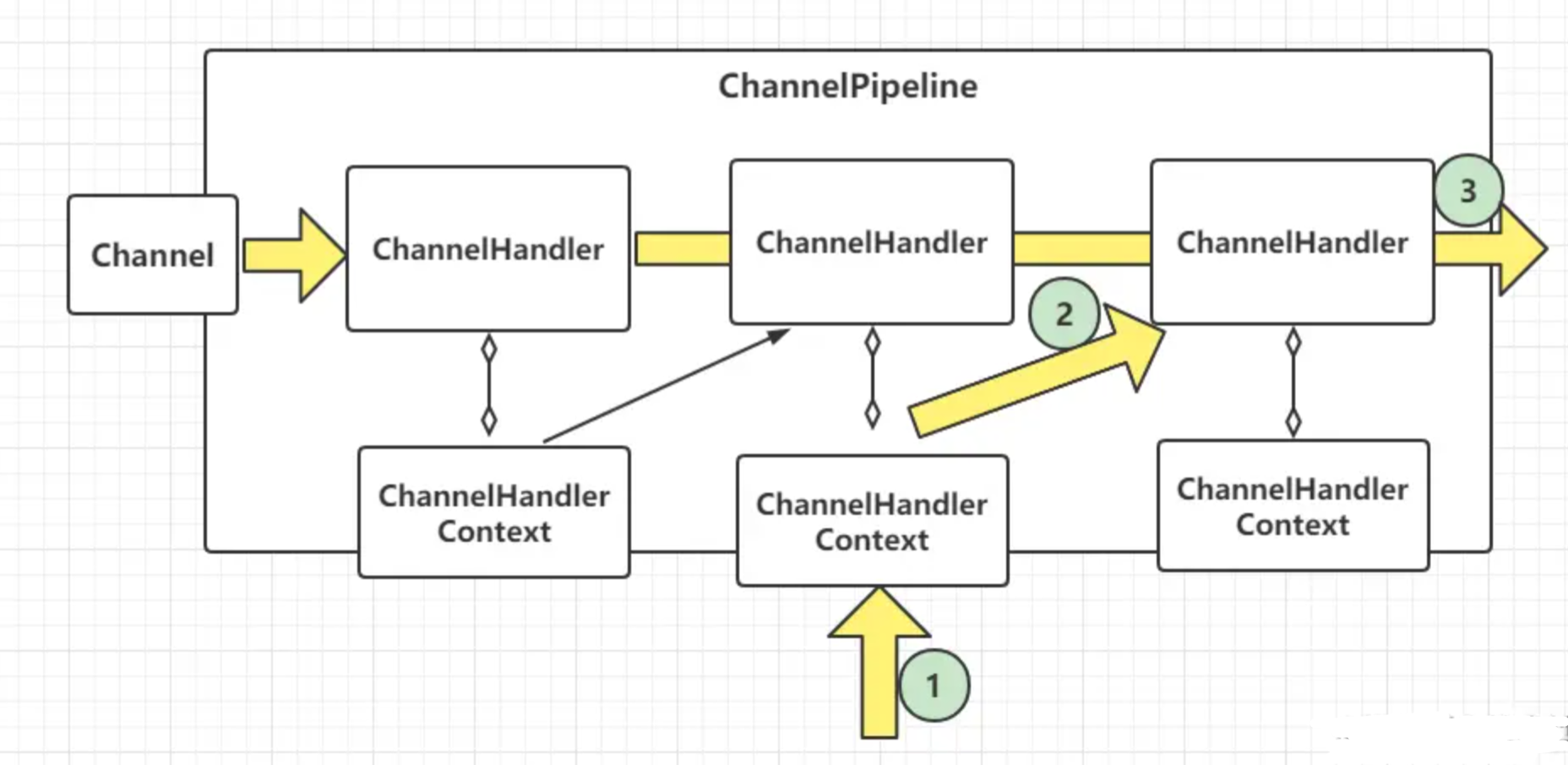
【Netty】ChannelPipeline源码分析(五)
文章目录 前言一、ChannelPipeline 接口1.1 创建 ChannelPipeline1.2 ChannelPipeline 事件传输机制1.2.1 处理出站事件1.2.2 处理入站事件 二、ChannelPipeline 中的 ChannelHandler三、ChannelHandlerContext 接口3.1 ChannelHandlerContext 与其他组件的关系3.2 跳过某些 Ch…...

并行计算技术解密:MPI和OpenMP的学习和应用指南
欢迎来到并行计算技术的奇妙世界!本指南将带您深入了解MPI(Message Passing Interface)和OpenMP(Open Multi-Processing)两种重要的并行计算技术,并为您提供学习和应用的指南。无论您是一个科研工作者、开发…...
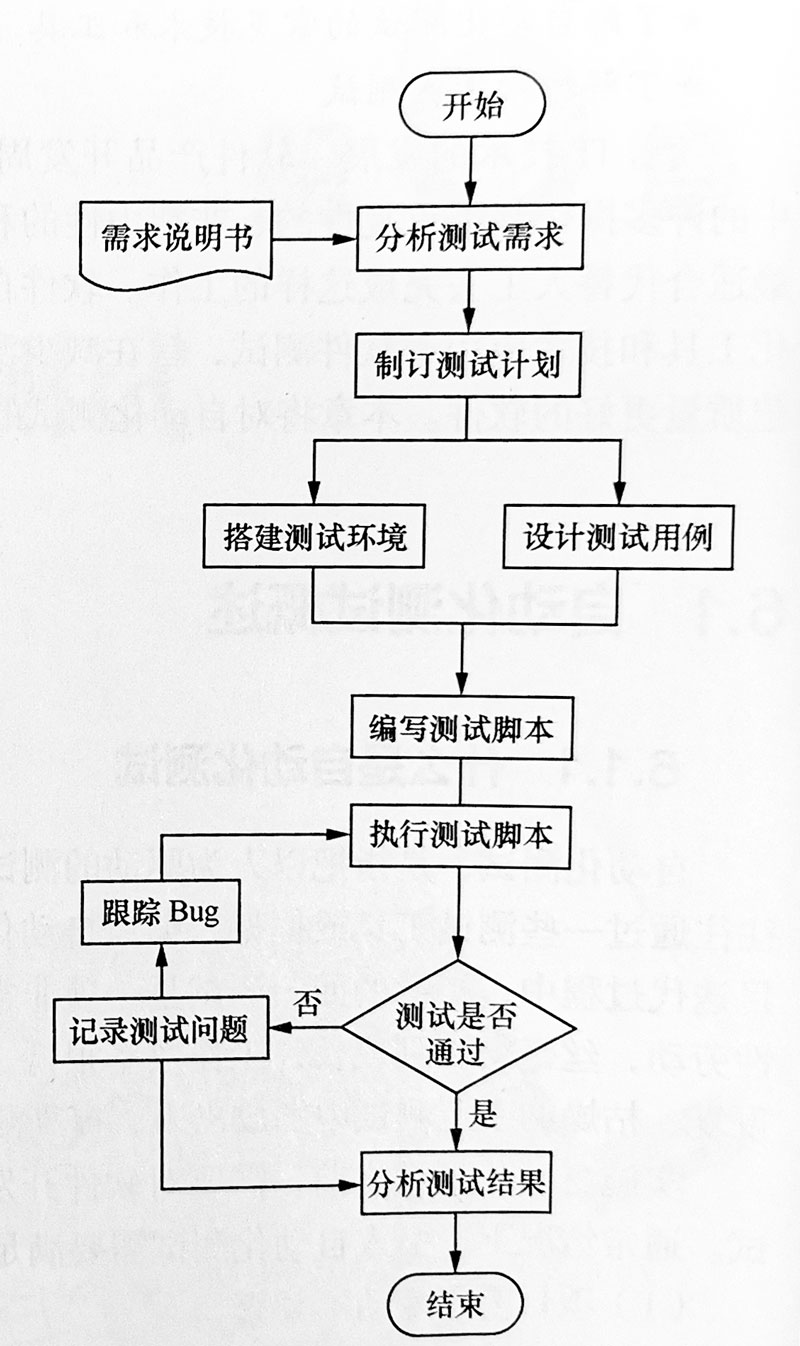
什么是自动化测试框架?我们该如何搭建自动化测试框架?
无论是在自动化测试实践,还是日常交流中,经常听到一个词:框架。之前学习自动化测试的过程中,一直对“框架”这个词知其然不知其所以然。 最近看了很多自动化相关的资料,加上自己的一些实践,算是对“框架”…...

Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics
Debezium报错处理系列之六十七:TopicAuthorizationException: Not authorized to access topics 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that the same history topic isn‘t sha…...
javaWebssh中小学课件资源系统myeclipse开发mysql数据库MVC模式java编程计算机网页设计
一、源码特点 java ssh中小学课件资源系统是一套完善的web设计系统(系统采用ssh框架进行设计开发),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。开发环境为TOMCAT…...

MySQL高级查询操作
文章目录 前言聚集函数分组查询:GROUP BY过滤:HAVING嵌套子查询比较运算中使用子查询带有IN的子查询SOME(子查询)ALL(子查询)EXISTS子查询 前言 查询语句书写顺序: 1、select 2、from 3、where 4、group by 5、having 6、order by 7、limit …...
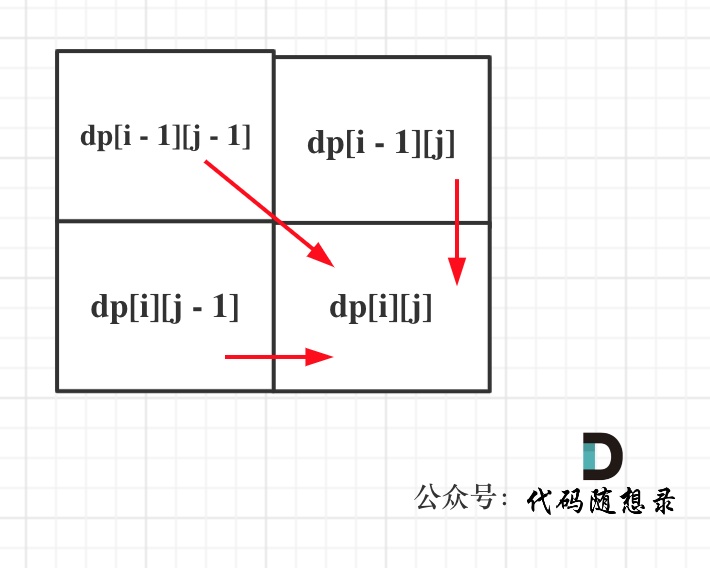
Day53【动态规划】1143.最长公共子序列、1035.不相交的线、53.最大子序和
1143.最长公共子序列 力扣题目链接/文章讲解 视频讲解 本题最大的难点还是定义 dp 数组 本题和718.最长重复子数组区别在于这里不要求是连续的了,但要有相对顺序 直接动态规划五部曲! 1、确定 dp 数组下标及值含义 dp[i][j]:取 text1…...

Three.js--》实现3d地球模型展示
目录 项目搭建 实现网页简单布局 初始化three.js基础代码 创建环境背景 加载地球模型 实现光柱效果 添加月球模型 今天简单实现一个three.js的小Demo,加强自己对three知识的掌握与学习,只有在项目中才能灵活将所学知识运用起来,话不多…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
