《程序员面试金典(第6版)》面试题 02.08. 环路检测(哈希法,双指针,检测链表是否有环)
题目描述
给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。若环不存在,请返回 null。
题目传送门:面试题 02.08. 环路检测
- 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
示例 1:

输入:head = [3,2,0,-4], pos = 1输出:tail connects to node index 1解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
进阶:
- 你是否可以不用额外空间解决此题?
解题思路与代码
-
这道题算是比较简单的一道题。检测链表是否存在环的最简单的一种方法是哈希法,其次就是快慢指针法。那么前者的空间复杂度可能会高些,但是代码结构简单易懂。
-
后者虽然说比前者稍微难点,但也没有难太多,多了一点点的思考量而已。
总的来说,这道题是一道好题,考验了你一点点的数学思维,与链表的实际操作
方案一:哈希法
这道题如果是单单的判断链表是否成环,那这道题就是一道简单题,如果还要让你去返回成环的开头节点,那这道题的难度就要上升了。
对于这道题,如果我们用了哈希法,那就是降维打击,因为我们利用unordered_set就可以直接帮你返回相同节点。
具体的代码如下:
class Solution {
public:ListNode *detectCycle(ListNode *head) {unordered_set<ListNode*> set;while(head){if(set.count(head)) return head;set.insert(head);head = head->next;}return nullptr;}
};

复杂度分析:
- 时间复杂度:O(n),其中n是链表节点的个数
- 空间复杂度:O(n),我们需要将链表的每一个节点放入集合中,所以是O(n)
方案二: 快慢指针法
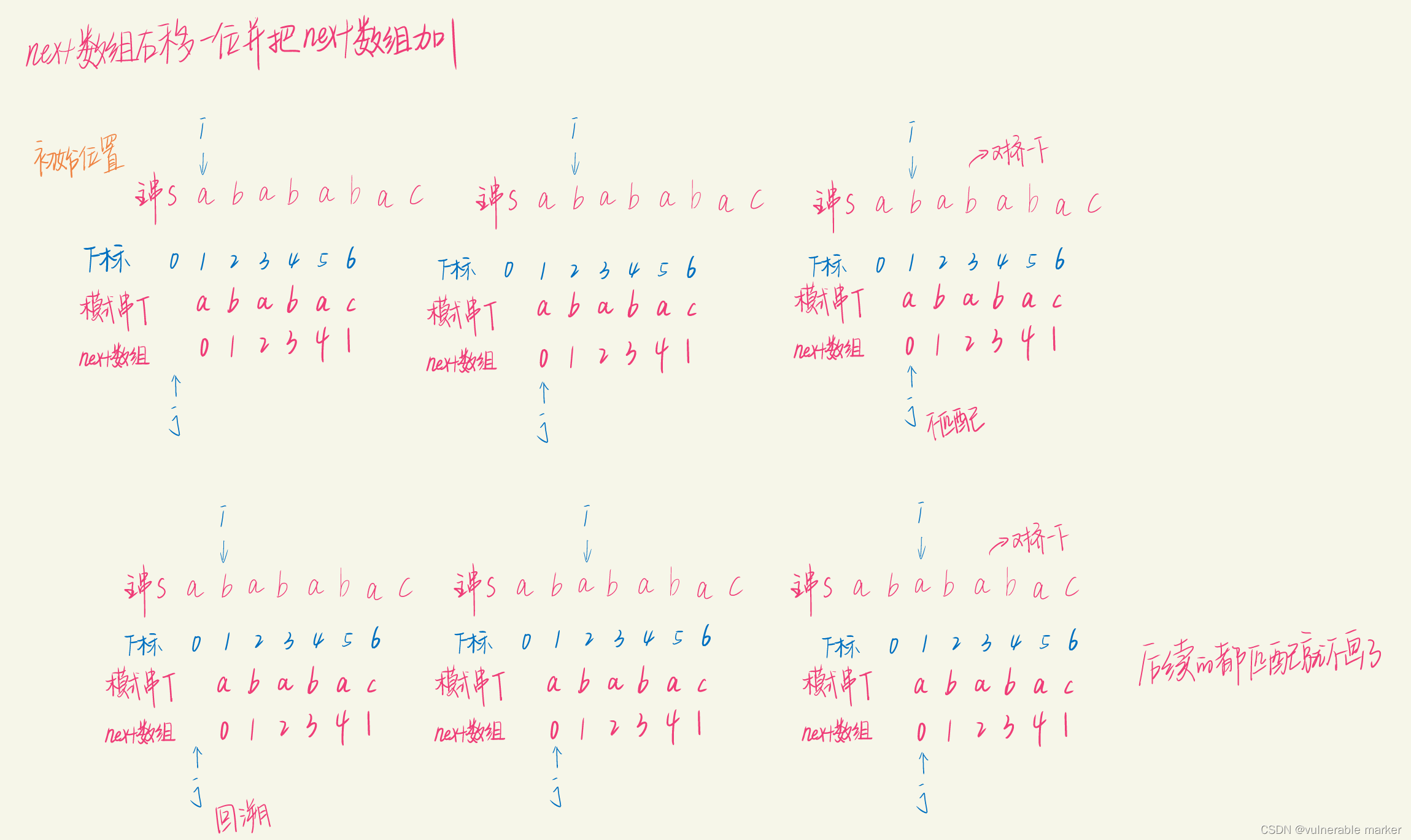
- 先解释一下这里的快慢指针法是什么意思。在这里,我们先设置两个指针,p1,p2。 p1一次走一格,p2一次走两个。因为他们走的步数不一样,所以,如果链表中有环存在了话,那么p1,p2一定不会相等。反之,如果有环,那p1,p2一定会相等。
那这道题的难点在成环节点,在距离头节点多少位置呢?首先,我们要画图分析。

-
我们设从头节点,到成环节点的距离为a,成环节点到p2追到p1的距离为b,被追到的p1节点距离再次回到成环节点的距离为c。
-
p2指针一次走两格,p1指针一次走一格,p2追上p1的时候,p2走过的距离是p1的两倍。
-
p1被追到时p2走了
a + n(b + c) + b,p1走了a + b所以不难得出这个等式:a + n(b + c) + b = 2(a + b) -
将这个等式变化一下便是 **a = c + (n-1)(b+c)**么。
看着这个图,我们来翻译一个这个数学等式的意思。
- 假设从头节点走了a步,到达了成环节点。便等于我在相遇节点走了 c 步 + n圈。
- 我们在p1节点与p2节点相遇的时候,再去设置一个p3节点让它等于头节点。这个时候,p3也一次走一步。
- 你看图,当p3在头节点走了a步的时候,是不是正好与p1在b的时候走了c步 + n圈呢?
具体代码如下:
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* p1 = head;ListNode* p2 = head;while(p2){p1 = p1->next;if(p2->next)p2 = p2->next->next;else return nullptr;if(p1 == p2) {ListNode* p3 = head;while(p3!=p1){p1 = p1->next;p3 = p3->next;}return p3;}}return nullptr;}
};

复杂度分析:
- 时间复杂度:O(N),N为节点的长度。因为你在实际推演的过程中会发现,p1指针走过的最长的路程也不会超过链表中节点的个数,而是等于节点的个数,所以时间复杂度是O(N)
- 空间复杂度:O(1),我们设置了几个变量而已,没有使用额外的数据结构,所以是O(1)。
总结
这道题目是一个经典的链表问题,经常出现在计算机科学和软件工程的面试和教程中。
这道题目的主要意义和重要性可以从以下几个方面来看:
-
数据结构理解与应用:这道题目需要你理解和操作链表这种基础数据结构。理解数据结构的特性和操作方法是编程和算法学习的基础。
-
双指针技巧:这道题目需要使用到双指针(快慢指针)的技巧。这是一个常用的算法设计策略,可以帮助解决一些看似复杂的问题。
-
算法分析:通过这道题目,你需要理解和分析算法的时间复杂度和空间复杂度。这道题的解决方案有一个很好的性质:它只需要常量的额外空间,且时间复杂度为线性。
-
问题解决和调试能力:这道题目也可以帮助你提升问题解决和调试的能力。理解为什么这个解决方案能够工作,对于提升你的算法设计和问题解决能力是非常有帮助的。
所以,这道题目的意义不仅仅是解决一个具体的问题,更重要的是通过这个问题来学习和提升你的数据结构知识,算法设计和问题解决能力。
最后的最后,如果你觉得我的这篇文章写的不错的话,请给我一个赞与收藏,关注我,我会继续给大家带来更多更优质的干货内容。
相关文章:

《程序员面试金典(第6版)》面试题 02.08. 环路检测(哈希法,双指针,检测链表是否有环)
题目描述 给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。若环不存在,请返回 null。 题目传送门:面试题 02.08. 环路检测 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链…...

软考A计划-试题模拟含答案解析-卷六
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...
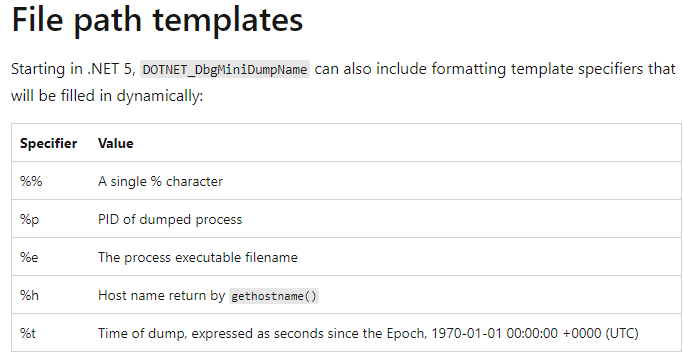
Linux 上的 .NET 崩溃了怎么抓 Dump
一:背景 1. 讲故事 训练营中有朋友问在 Linux 上如何抓 crash dump,在我的系列文章中演示的大多是在 Windows 平台上,这也没办法要跟着市场走,谁让 .NET 的主战场在工控 和 医疗 呢,上一张在 合肥 分享时的一个统计图…...

QT桌面项目(状态栏和导航栏设置)
文章目录 前言一、状态栏二、导航栏三、同时添加状态栏和导航栏总结 前言 为了和我们这个项目做的更加真实,这里为我们的项目添加上状态栏和导航栏让他变成更加接近手机的桌面效果。 一、状态栏 这个状态栏就是显示时间和wifi状态,电池电量的…...

数据链路层:点对点协议PPP
数据链路层:点对点协议PPP 笔记来源: 湖科大教书匠:点对点协议PPP 声明:该学习笔记来自湖科大教书匠,笔记仅做学习参考 数据链路层只负责直接相连的两个结点之间的通信 PPP是点对点数据链路层协议 用户通过ISP接入因特…...

C/C++读取txt文件中的float数据并用指针存储
C语言中读取txt文件中的数据 以下是一个简单的示例代码,演示如何在C语言中读取txt文件中的数据: #include <stdio.h>int main() {FILE *fp;char buffer[100];// 打开文件fp fopen("example.txt", "r");// 如果文件打开失败…...
对KMP算法的一点碎碎念——上篇
对KMP算法的一点碎碎念——上篇 文章目录 对KMP算法的一点碎碎念——上篇1. KMP 算法 Next数组 求解问题1.1 前置知识-最长公共前后缀LCP1.1.1 前缀与后缀1.1.2 最长公共前后缀LCP 1.2 手算法求解 Next数组值(3种常见情况)1.2.1 情况1: next数组 正常存放匹配字符的长度情况1的…...

算法---边界着色
题目 给你一个大小为 m x n 的整数矩阵 grid ,表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。 两个网格块属于同一 连通分量 需满足下述全部条件: 两个网格块颜色相同 在上、下、左、右任意一个方向上…...

二叉排序树的查找、插入、删除
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的定义 二叉排序树的定义 二叉排序树(Binary Sort Tree, BST),也称二叉查找树。 二叉排序树或者是一棵空树,或者是一棵具有下列特性的非空二叉…...
《Opencv3编程入门》学习笔记—第三章
《Opencv3编程入门》学习笔记 记录一下在学习《Opencv3编程入门》这本书时遇到的问题或重要的知识点。 第三章 HighGUI图形用户界面初步 一、图像的载入、显示和输出到文件 (一)OpenCV的命名空间 简单的OpenCV程序标配: #include <o…...
如何从Ubuntu Linux中删除Firefox Snap?
Ubuntu Linux是一款广受欢迎的开源操作系统,拥有强大的功能和广泛的应用程序选择。默认情况下,Ubuntu提供了一种称为Snap的软件打包格式,用于安装和管理应用程序。Firefox是一款流行的开源网络浏览器,而Firefox Snap是Firefox的Sn…...
数学建模的初阶-快速上手
目录 第一步:明确问题 第二步:选择建模方法 第三步:收集数据 第四步:构建数学模型 第五步:模型验证与评估 数学建模软件推荐 统计模型 (1) 线性回归模型 (2) 逻辑回归模型 (3) 时间序列模型 优化模型 (1) …...
)
复习向 C/C++ 编程语言简介和概括(C++复习向p1)
文章目录 C 编程语言C 和 C 关系标准的 C 组成ANSI 标准比较重要的标准化时间 C 编程语言 是一种静态类型的、编译式的、通用式的、大小写敏感、不规则的编程语言支持过程化编程,面向对象,泛型编程 C 和 C 关系 C 是 C 的一个超集,任何合法…...

DRF之过滤,排序,分页
一、权限组件源码解读 1.继承了APIView 才有的---》执行流程---》dispatch中----》三大认证 APIView的dispatch def initial(self, request, *args, **kwargs):self.perform_authentication(request)self.check_permissions(request)self.check_throttles(request) 2 读…...

我的Redis学习,共写了14篇博客文章
早在19和20年全面学习SpringBoot相关技术知识时也曾经有学习到Redis,主要是看了几家的视频教程,但是未曾有具体的实践,后来再学习到Docker和Spring Session框架的Redis存储时,又稍微的实践了一丢丢,所有的实践也就仅此…...
mPython软件使用指南
①软件界面 一、软件界面的介绍 1.模式切换 硬件编程 Python3.6 Jupyter python3.6模式细节补充(一般不使用该模式,此处可跳过) Python3.6模式的界面 左侧指令分类栏 Python3.6模式的图形化指令分类分为: Python语法基础相关指令&…...

龙芯2K1000实战开发-系统配置详解
目录 概要 整体架构流程 技术名词解释 技术细节 编辑 总结...
【一起撸个DL框架】5 实现:自适应线性单元
CSDN个人主页:清风莫追欢迎关注本专栏:《一起撸个DL框架》GitHub获取源码:https://github.com/flying-forever/OurDLblibli视频合集:https://space.bilibili.com/3493285974772098/channel/series 文章目录 5 实现:自适…...

开箱即用的工具函数库xijs更新指南(v1.2.6)
xijs 是一款开箱即用的 js 业务工具库, 聚集于解决业务中遇到的常用函数逻辑问题, 帮助开发者更高效的开展业务开发. 接下来就和大家一起分享一下 v1.2.6 版本的更新内容以及后续的更新方向. 贡献者列表: 1. 计算变量内存calculateMemory 该模块主要由 zhengsixsix 贡献, 我们可…...
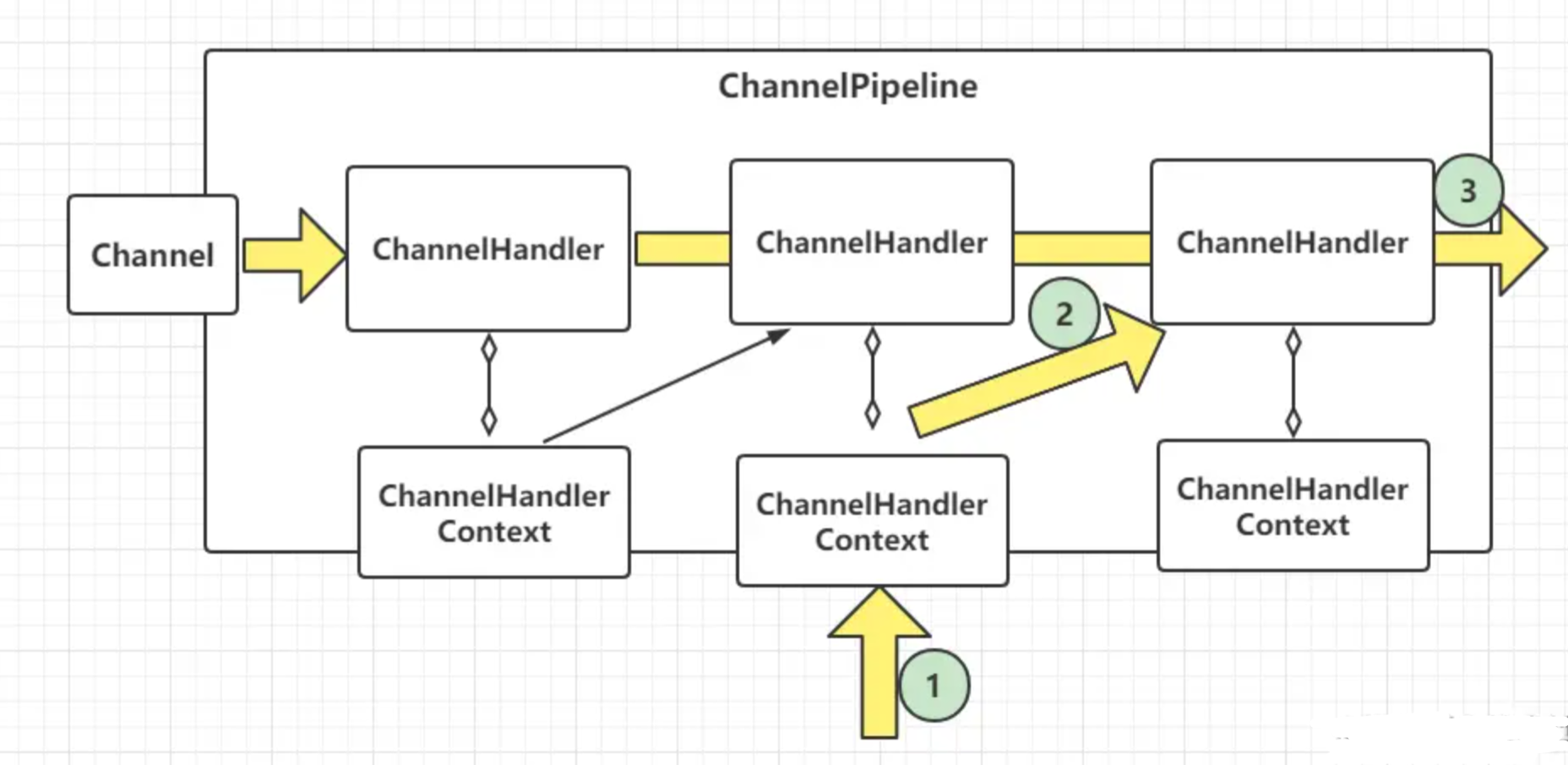
【Netty】ChannelPipeline源码分析(五)
文章目录 前言一、ChannelPipeline 接口1.1 创建 ChannelPipeline1.2 ChannelPipeline 事件传输机制1.2.1 处理出站事件1.2.2 处理入站事件 二、ChannelPipeline 中的 ChannelHandler三、ChannelHandlerContext 接口3.1 ChannelHandlerContext 与其他组件的关系3.2 跳过某些 Ch…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
