数据结构——第二章 线性表(1)——顺序结构
线性表
- 1. 线性表
- 1.1 线性表的定义
- 1.1.1 访问型操作
- 1.1.2 加工型操作
- 1.2 线性表的顺序存储结构
- 1.2.1 定义顺序表数据类型方法1
- 1.2.2 定义顺序表数据类型方法2
- 1.3 顺序表的基本操作实现
- 1.3.1 顺序表的初始化操作
- 1.3.2 顺序表的插入操作
- 1.3.3 顺序表的删除操作
- 1.3.4 顺序表的更新操作
- 1.3.5 顺序表的定位操作
- 1.3.6 顺序表的遍历操作
- 1.3.7 顺序表的创建操作
1. 线性表
具有1:1的线性关系的数据对象称为线性表。
1.1 线性表的定义
线性表是最简单的一种线性结构,具有如下特征。
(1)线性表中必存在唯一的一个“第一元素”。
(2)线性表中必须存在唯一的一个“最后元素”。
(3)除了最后元素之外,其余元素均有唯一的直接后继。
(4)除了第一个元素之外,其余元素均有唯一的直接前驱。
线性表的抽象数据类型定义形式:
ADT List
{ 数据对象:
D={ai | ai∈ElemSet,i=1,2,…,n>=0}
{ n为线性表的表长,即数据元素的个数;n=0时的线性表为空表。}
数据关系:
R ={ <ai-1,ai> |ai-1,ai∈D, i=2,3,…,n }
{ 设线性表为(a1,a2,…,ai,…,an),称i为ai在线性表中的位序}
基础操作:
初始化操作
销毁操作
访问型操作
加工型操作
} ADT List
&L表示会引起线表的变化,L表示不会引起线标的变化。
下面分别介绍线性表的各个基本操作的初始条件和实现的功能
1.1.1 访问型操作
这类操作只是访问线性表中的元素,并没有改变线性表。
(1)判断线性表是否为空:ListEmpty(L)。
初始条件:线性表L存在。
操作结果:若L为空表,则返回TRUE,否则返回FALSE。
(2)求线性表的长度:ListLength(L)
初始条件:线性表存在。
操作结果:放回L中的数据元素的个数。
(3)得到线性表中某个位置上的元素:GetElem(L,i,&e)。
初始化条件:线性表L已存在,且 1<=i<=LengthList(L)。
操作结果:用e返回L中第i个元素的值。
(4)通知比较,寻找位置:LocateElem(L,e,compare())。
初始条件:线性表L已存在,e为给定值,compare()是元素比较函数。
操作条件:返回L中第1个与e满足关系compare()的元素的位序。若这样的元素不存在,则返回值-1 。
(5)遍历线性表:ListTraverse(L)。
初始条件:线性表L已存在。
操作结果:依次访问L中的每个元素。
1.1.2 加工型操作
这类操作改变了原有的线性表。
(1)初始化操作:InitList(&L)。
操作结果:构造一个空的线性表L。
(2)销毁操作:DestroyList(&L)。
初始条件:线性表L已存在。
操作结果:销毁线性表L。
(3)线性表置空:CleaerList(&L)。
初始化条件:线性表L已存在。
操作结果:将L重置为空表,L由非空为空。
(4)修改线性表中某个位置上的元素置:PutElem(&L,i,e)。
初始化条件:线性表L已存在,且1<=i<=LengthList(L)。
操作结果:给L中第i个元素赋值e。L中的第i个元素的值发生了改变。
(5)在第i个位置上插入数据元素:ListInsert(&L,i,e)。
初始条件:线性表L已存在,且1<=i<=LengthList(L)+1.
操作结果:在L的第i个元素之前插入新的元素e,并将L的长度增1 。
(6)将线性表的第i个元素删除:ListDelete(&L,i,e)。
初始条件:线性表L已存在,且1<=i<=LengthList(L)。
操作结果:删除L的第i个元素,并且用e 返回其值,同时将L的长度减1 。
其中最重要的是插入操作和删除操作。
1.2 线性表的顺序存储结构
线性表的顺序存储结构是用一组连续的存储空间存放线性表中的各个数据元素,并用位置相邻的存储空间关系表示线性表中数据元素的直接前驱和直接后继的次序关系,称为顺序表。
1.2.1 定义顺序表数据类型方法1
包括以下数据成员:
(1)一片连续的存储空间(数组用于存放数据元素)。
(2)线性表的容量(数组的大小防止溢出)。
(3)线性表的长度(已经存入到数组中的数据元素个数)。
1.2.2 定义顺序表数据类型方法2
包括以下数据成员:
(1)一片连续的存储空间的起始地址(存放数组的起始地址)。
(2)线性表的容量(数组的大小防止溢出)。
(3)线性表的长度(已经存入到数组中的数据元素个数)。
对于两种存储结构的不同描述。第一种容易理解,使用相对简单,但是数组是顺序表的成员,大小固定,因此缺乏灵活性。第二种理解起来有一定难度,数组不是顺序表的成员,可根据实际问题的需要吗,在初始化操作中自定义数组的大小,因此具有较好的灵活性。
1.3 顺序表的基本操作实现
为了使数据结构中的操作具有很好的健壮性,在函数的定义中,通常用函数值表示操作的成功与失败。函数值为1,表示成功;函数值为0,表示失败。有时候为了方便起见,也可以将操作的结果作为函数的返回值。
1.3.1 顺序表的初始化操作
顺序表的初始化操作是完成一片连续空间的申请,将空间的起始地址、容量大小和数据个数0依次存放到顺序表中对应成员中。
算法的实现:
int initSqList(SqList* L, int max)
{L->data = (STD*)malloc(max * sizeof(STD));if (L->data == NULL){perror("initSqList::");exit(0);}L->length = 0;L->listSize = max;return 1;//表示初始化操作成功
}
函数exit(0)的功能是结束程序的执行。为什么当动态申请存储空间失败时不用“return 0;”,而是调用函数exit(0)?原因是既然顺序表的初始化失败了,其他的有关对顺序表的操作都不可能正确执行,因此退出程序,并放回到系统。
【算法分析】
该算法不涉及基本操作的循环执行,算法的时间复杂度为T(n) = O(1)。
1.3.2 顺序表的插入操作
顺序表的插入操作是将某个学生数据插入顺序表中指针成员指向数组的给定位置,并将顺序表的长度成员加1
算法实现如下:
int insertSqList(SqList* L, int i, STD x)//i是插入位置,对应下标是i-1
{//插入失败的情况判断if (i<1 || i>L->length + 1){printf("插入位置异常!\n");return 0;}if (L->length >= L->listSize){printf("容量不够!\n");return 0;}//将区间[i-1,L->lenght-1]内的一组数据元素向后移动一个位置for (int k = L->length - 1; k >= i - 1; k--){L->data[k + 1] = L->data[k];}//将待插入数据放入指定位置i,即下标i-1上L->data[i - 1] = x;//长度加1L->length++;//插入成功return 1;
}
寻找插入位置,将数据插进来,需移动数据元素。
最好情况(i=n+1);基本语句执行0次,时间复杂度为O(1);
最坏情况(i=1);基本语句执行n次,时间复杂度为O(n);
平均情况(1<=i<=n+1):等概率pi =1/(n+1)。
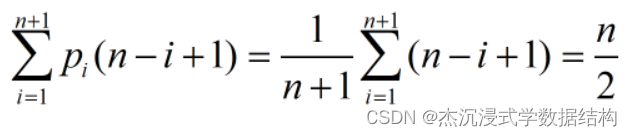
算法的时间复杂度为T(n)=O(n) 。
1.3.3 顺序表的删除操作
顺序表的删除操作是将顺序表中指针成员指向数组的给定位置的数组元素删除,并将数据个数减1.
算法实现如下:
int deleteSqList(SqList* L, int i, STD* x)
//i表示接受删除数据元素位置的整形变量
//x是将被删除的数据元素存回到主调函数中某个变量的指针变量
{//判断删除失败的条件是否成立if (L->length == 0){printf("没有数据,不能删除!\n");return 0;}if (i <= 0 || i > L->length){printf("位置异常,不能被删除\n");return 0;}//将被删除的数据元素存放到*x中*x = L->data[i - 1];//将区间[i,L->length-1]内的一组数据元素向前移动一个位置for (int k = i; k < L->length; k++){L->data[k - 1] = L->data[k];}//长度减1L->length--;//删除成功return 1;
}
【算法分析】
寻找删除位置,将数据删除,需移动数据元素。
最好情况(i=n+1);基本语句执行0次,时间复杂度为O(1);
最坏情况(i=1);基本语句执行n次,时间复杂度为O(n);
平均情况(1<=i<=n):等概率pi =1/(n)。
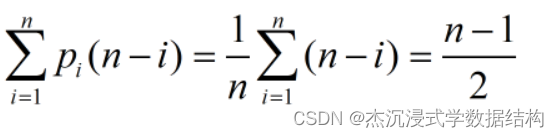
算法的时间复杂度为T(n)=O(n) 。
1.3.4 顺序表的更新操作
顺序表的更新操作是用新数据替换指定位置的数据。
int updateSqList(SqList* L, int i, STD x)
{//更新失败条件的判断if (L->length == 0){printf("没有数据,不能更新!\n");return 0;}if (i<1 || i>L->length){printf("位置不合适!\n");return 0;}//开始更新数据L->data[i - 1] = x;//更新成功return 1;
}
【算法分析】
该算法的操作不涉及循环,均为顺序执行,所以算法的时间复杂度为T(n)=O(1)。
1.3.5 顺序表的定位操作
顺序表的定位操作是根据给定的条件得到某个数据元素的位置。定位操作又称为查找操作。
位置从1开始
算法实现如下:
int locationSqList(SqList* L, char* newid)
{int i;//查找失败的条件判断if (L->length == 0){printf("没有数据!\n");return 0;}for (int i = 0; i < L->length; i++){//查找成功的条件的判断if (strcmp(L->data[i].name, newid) == 0){return i + 1;}}//查找失败return 0;
}
【算法分析】
按照给定的条件,查找相应的数据元素,需逐个判断。最好的情况是O(1);最坏的情况是O(n)。
等概率加权平均是O(n)。
1.3.6 顺序表的遍历操作
顺序表的遍历操作是输出顺序表中存放的所有数据元素。
分析:遍历操作不会引起顺序表的变化,遍历函数只需一个形参
算法实现如下:
int dispSqlist(SqList* L)
{if (L->length == 0){printf("没有数据!\n");return 0;}for (int i = 0; i < L->length; i++){printf("%10s%7.2f\n", L->data[i].name, L->data[i].score);}return 1;
}
【算法分析】
显示所有的数据,必须逐个依序显示,时间复杂度为T(n)=O(n)。
1.3.7 顺序表的创建操作
顺序表的创建操作依序存入顺序表中。
一共有两种算法:
算法1:调用初始化函数和插入函数创建顺序表
void createSqList1(SqList* L, int maxsize)
{int n = 0;STD x;char yn;//调用初始化函数,创建空表——申请空间来存储表的数据do{printf("请输入第%d个学生的姓名和分数,用空格隔开:", n + 1);scanf("%s%f", x.name, &x.score);//空度回车,以便下次正确读入数据getchar();//调用插入函数,将数据插入到尾部insertSqList(L, ++n, x);printf("继续输入吗?Y/N\n");scanf("%c", &yn);} while (yn == 'Y' || yn == 'y');
}
算法2:直接读取数据来创建顺序表
void createSqList2(SqList* L, int maxsize)
{int n=0;STD x;char yn;//初始化L->data = (STD*)malloc(maxsize * sizeof(STD));if (L->data == NULL){perror("createSqList2::");return 0;}L->listSize = maxsize;L->length = 0;//读取数据并插入do{printf("请输入第%d个学生的姓名和分数,用空格隔开:", n + 1);scanf("%s%f", x.name, &x.score);//空度回车,以便下次正确读入数据getchar();L->data[n] = x;if (n >= L->listSize - 1){break;}else{n++;}printf("继续输入吗?\n");scanf("%c", &yn);} while (yn == 'Y' || yn == 'y');
}
相关文章:
数据结构——第二章 线性表(1)——顺序结构
线性表1. 线性表1.1 线性表的定义1.1.1 访问型操作1.1.2 加工型操作1.2 线性表的顺序存储结构1.2.1 定义顺序表数据类型方法11.2.2 定义顺序表数据类型方法21.3 顺序表的基本操作实现1.3.1 顺序表的初始化操作1.3.2 顺序表的插入操作1.3.3 顺序表的删除操作1.3.4 顺序表的更新操…...
YOLO 格式数据集制作
目录 1. YOLO简介 2.分割数据集准备 3.代码展示 整理不易,欢迎一键三连!!! 1. YOLO简介 YOLO(You Only Look Once)是一种流行的目标检测和图像分割模型,由华盛顿大学的 Joseph Redmon 和 Al…...

基于linux内核的驱动开发
1 字符设备驱动框架 1.1字符设备 定义:只能以一个字节一个字节的方式读写的设备,不能随机的读取设备中中的某一段数据,读取数据需要按照先后顺序。(字符设备是面向字节流的) 常见的字…...
找不到工作的测试员一大把,大厂却招不到优秀软件测试员?高薪难寻测试工程师。
测试工程师招了快一个月了,实在招不到合适的,已经在被解雇的边缘了。。。” 初级测试工程师非常多,但真正掌握测试思维、能力强的优秀测试太少了! 据我所知, 当下的测试人员不少状态都是这样的: 在工作中…...
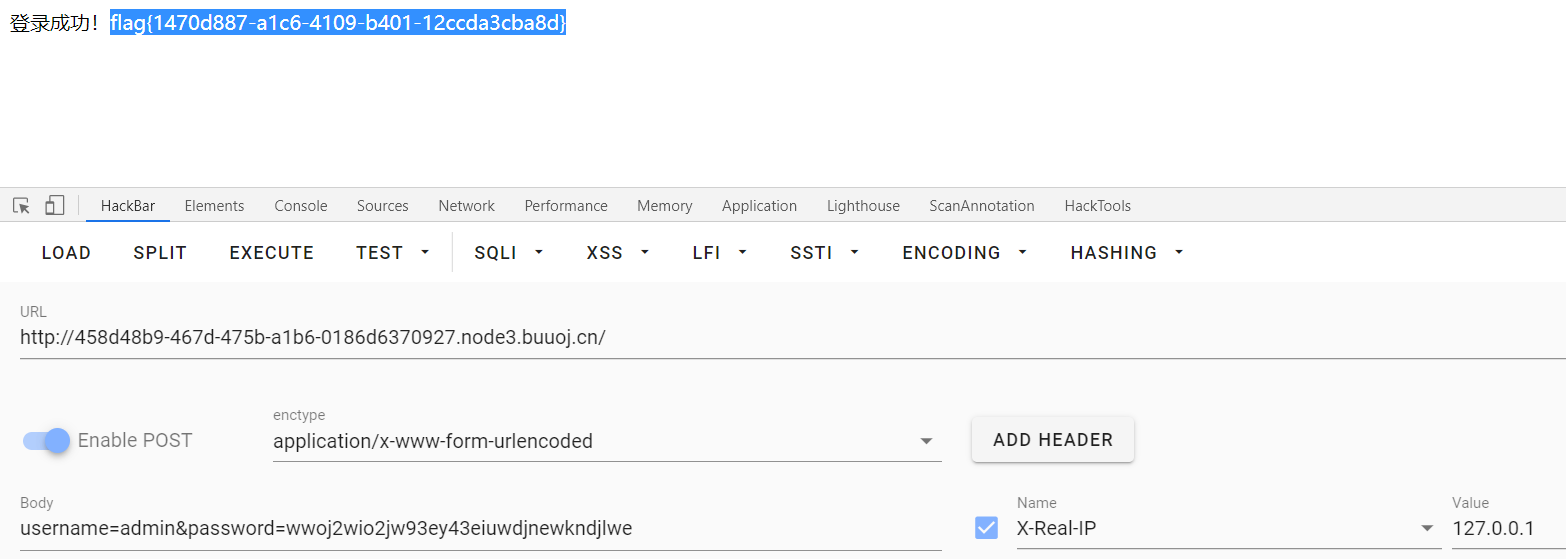
buuctf Basic
buuctf Basic 1.Linux Labs 根据提示我们可以知道需要远程连接linux服务器,这里使用xshell进行如下配置 输入ssh的用户名root,密码123456 连接成功 构造命令 ls …/ 查看文件 查看flag cat …/flag.txt 为flag{8fee8783-1ed5-4b67-90eb-a1d603a0208…...
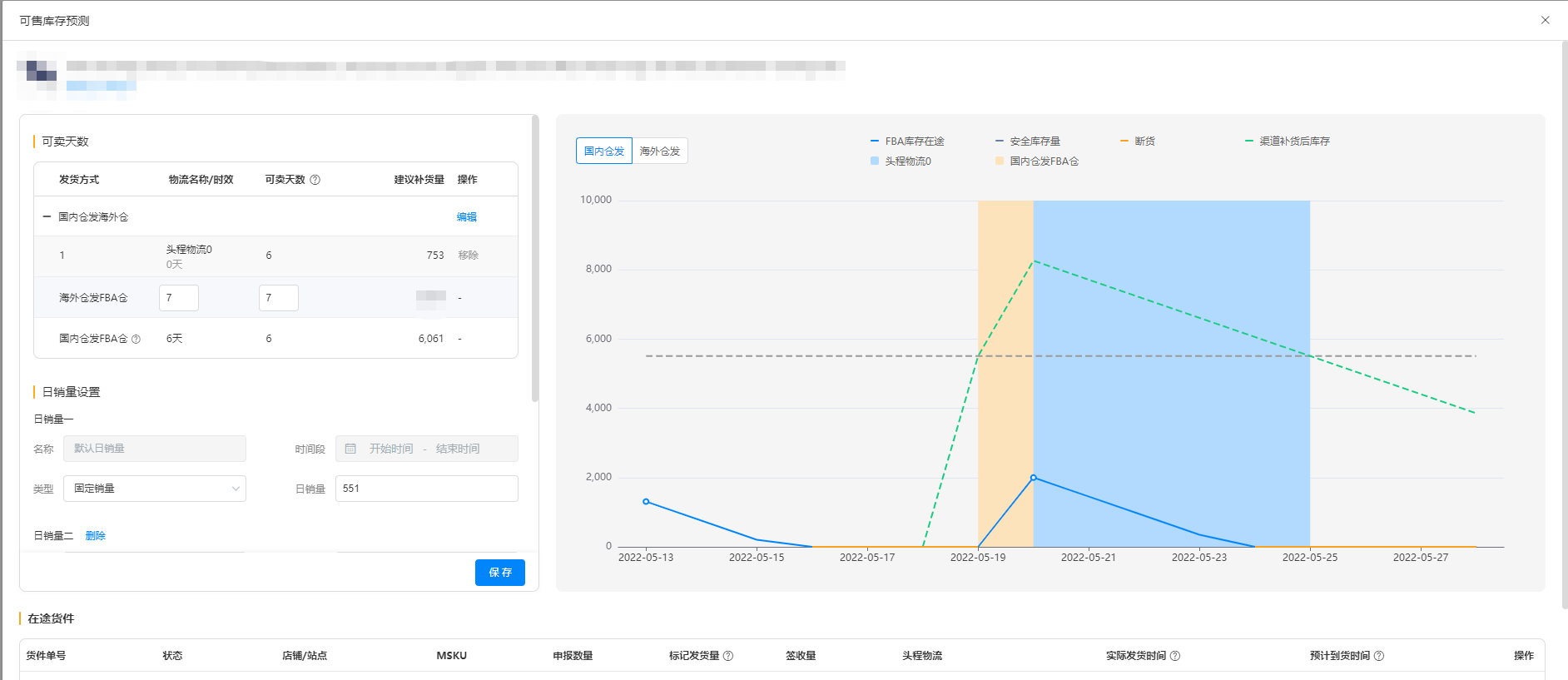
赛狐ERP|亚马逊产品缺货怎么办?该如何补救?
由于物流时效的延长,运输成本的增加,亚马逊的仓储限制等各种原因,断货问题很常成为亚马逊卖家的普遍困扰。那么亚马逊产品缺货应该怎么办!1、提高产品价格:除了卖自己的Listing此外,提高产品价格也是一种保…...

《Elasticsearch源码解读与优化实战》张超-读书笔记
写在前面 好久没更新博客了,应届狗没办法啊╮(╯▽╰)╭为了秋招搞了小半年,从去年5月到现在搞了两段实习(京东、游戏公司),最终年前拿到一家还不错的offer,现在已经入职实习了,不出意外的话以…...
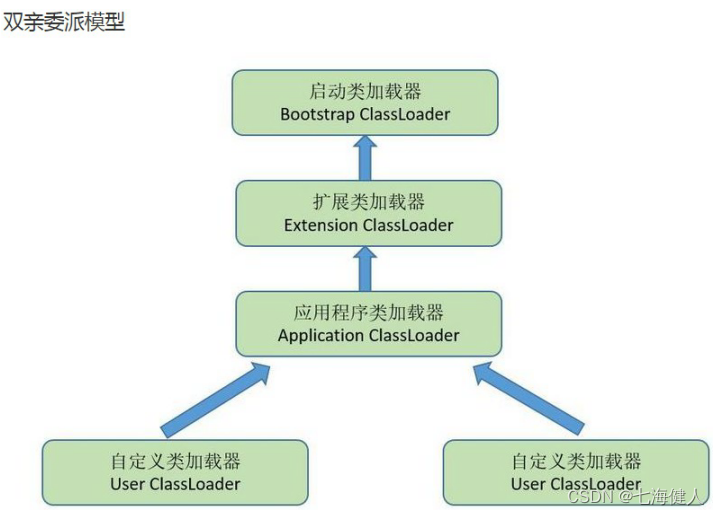
编码踩坑——运行时报错java.lang.NoSuchMethodError / 同名类加载问题 / 双亲委派【建议收藏】
本篇介绍一个实际遇到的排查异常的case,涉及的知识点包括:类加载机制、jar包中的类加载顺序、JVM双亲委派模型、破坏双亲委派模型及自定义类加载器的代码示例;问题背景业务版本,旧功能升级,原先引用的一个二方包中的du…...
软件测试选Python还是Java?
目录 前言 1、先从一门语言开始 2、两个语言的区别 3、两个语言的测试栈技术 4、如何选择两种语言? 总结 前言 对于工作多年的从业者来说,同时掌握java和Python两门语言再好不过,可以大大增加找工作时的选择范围。但是对于转行的人或者…...
“2023数据安全智能化中国行”活动,开幕即高能
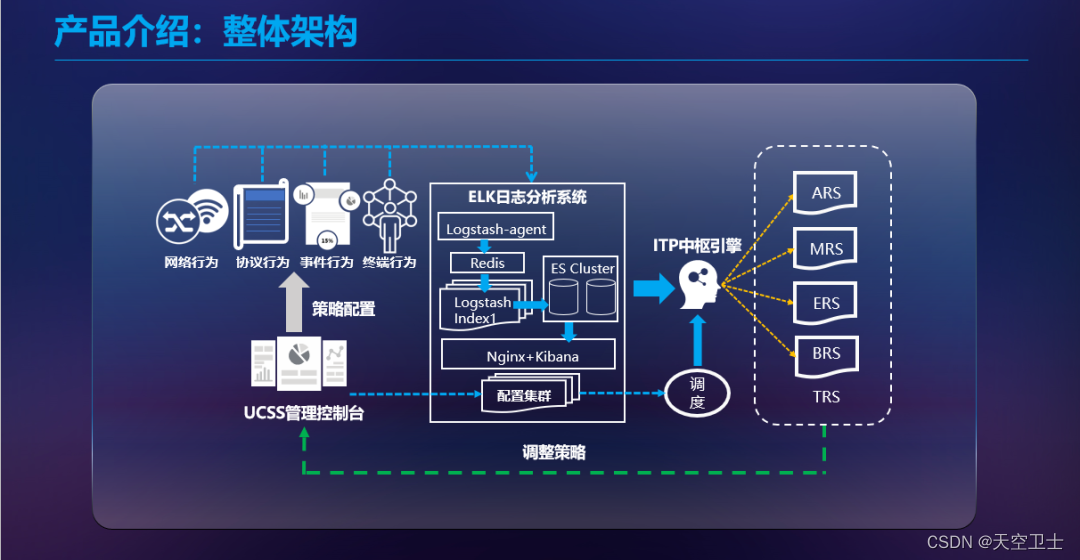
工信部等16部门近日发布的《关于促进数据安全产业发展的指导意见》提出,到2025年,数据安全产业基础能力和综合实力明显增强,数据安全产业规模超过1500亿元,年复合增长率超过30%。到2035年,数据安全产业进入繁荣成熟期。…...

机器人操作规划——Deep Visual Foresight for Planning Robot Motion(2017 ICRA)
1 简介 model-based RL方法,预测Action对图像的变化,以push任务进行研究。 采用完全自监督的学习方式,不需要相机标定、3D模型、深度图像和物理仿真。 2 数据集 采用几百个物体、10个7dof机械臂采集了包括5万个push attempts的数据集。 每…...

go 连接redis集群
最近用redis shake做redis数据迁移,由于redis提供的客户端没有用于查看集群的工具,且我部署的redis集群是基于k8s来构建的,没有使用ingress做转发,所以只能在k8s内部访问集群,于是我先用gogin框架编写了访问redis集群的…...

LeetCode 146. LRU 缓存
原题链接 难度:middle\color{orange}{middle}middle 题目描述 请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCacheLRUCacheLRUCache 类: LRUCache(intcapacity)LRUCache(int capacity)LRUCache(intcapacity) 以 正整数 …...
【mac】在m2 mbp上通过Parallels Desktop安装ubuntu22.04
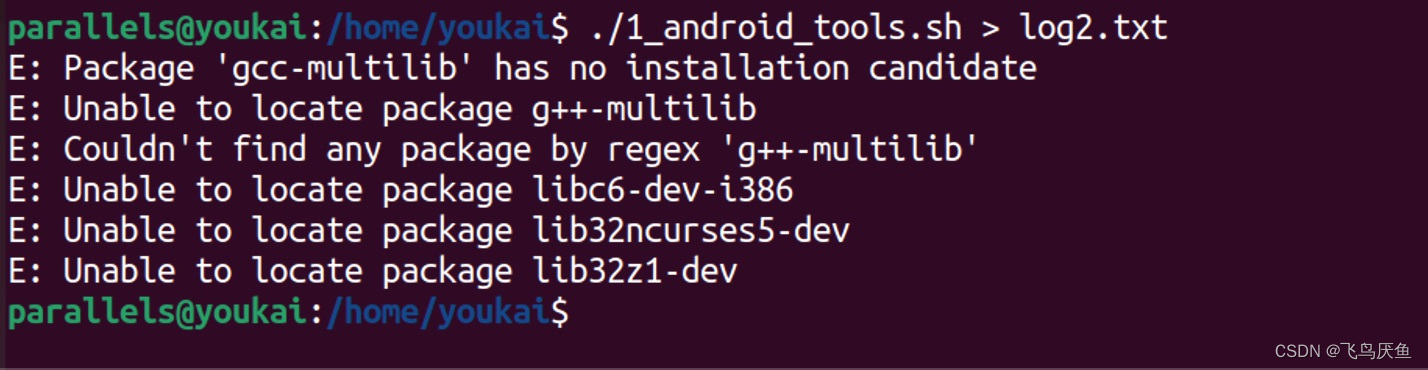
文章目录前言一、参考文章二、版本信息三、方法1:通过ubuntu官网提供的iso安装3.1 配置服务器3.2 安装图形界面四、方法2:通过Parallels Desktop提供的安装包五、 小工具5.1 调整应用栏图标大小5.2 ubuntu获取mac的剪切板5.3 调整terminal字体大小5.4 安装samba5.5 ubuntu连接m…...
C++类和对象,初见类
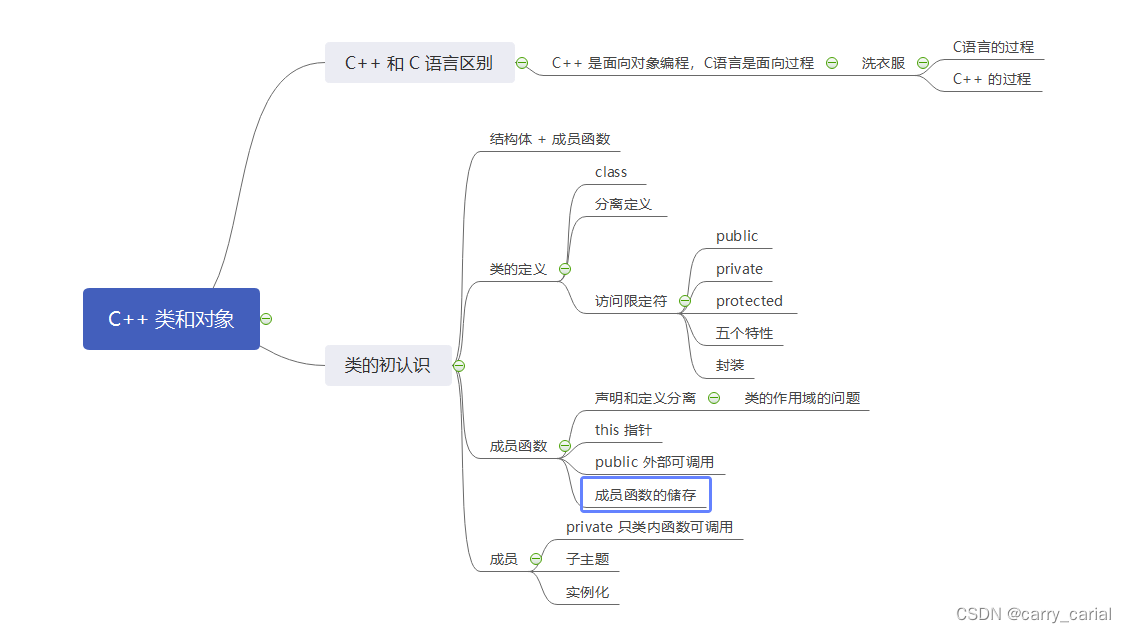
坚持看完,结尾有思维导图总结 这里写目录标题C语言和 C 的区别类的定义类的初认识类的内容访问限定符类的作用域类的实例化类中的 this 指针总结C语言和 C 的区别 C 的祖师爷除了在 C语言的基础上化简了一些复杂操作 更为重要的是,两个语言实现的过程是…...
Redis常用数据结构及应用场景
1.总体结构 Redis中的数据,总体上是键值对,不同数据类型指的是键值对中值的类型。 2.string类型 Redis中最基本的类型,它是key对应的一个单一值。二进制安全,不必担心由于编码等问题导致二进制数据变化。所以redis的string可以…...

C++虚继承内存布局
C菱形继承内存布局 编译器:Visual Studio 2019 关于如何查看内存布局 B class B { public:B(): _ib(10), _cb(B){cout << "B()" << endl;}B(int ib, char cb): _ib(ib), _cb(cb){cout << "B(int,char)" << endl;}vi…...
IO模型--从BIO、NIO、AIO到内核select、poll、epoll剖析
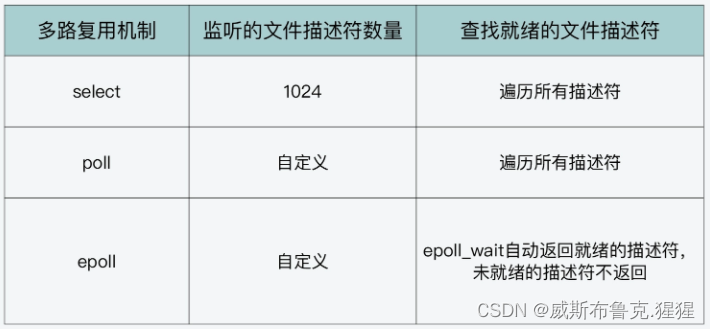
IO基本概述 IO的分类 IO以不同的维度划分,可以被分为多种类型;从工作层面划分成磁盘IO(本地IO)和网络IO; 也从工作模式上划分:BIO、NIO、AIO;从工作性质上分为阻塞式IO与非阻塞式IO;…...

Zebec完成BNB Chain以及Near链上协议部署,多链化进程加速
从去年开始,Zebec 就开始以多链的形式来拓展自身的流支付生态,一方面向更多的区块链系统拓展自身流支付协议,即从Solana上向EVM链上对协议与通证等进行迁移与拓展。目前基本完成了在BNB Chain以及Near上的合约部署,且能够在这些EV…...

wpscan常见的使用方法
目录 简单介绍 暴力破解 信息收集 指定用户爆破 命令集合 简单介绍 Wordpress是一个以PHP和MySQL为平台的免费自由开源的博客软件和内容管理系统。 WPScan是Kali Linux默认自带的一款漏洞扫描工具,它采用Ruby编写,能够扫描WordPress网站中的多种安…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
