常微分方程ODE和Neural Ordinary Differential Equations
微分方程(英語:Differential equation,DE)是一種數學方程,用來描述某一類函数與其导数之间的关系。微分方程的解是一個符合方程的函數。而在初等数学的代数方程裡,其解是常数值。
常微分方程(英語:ordinary differential equation,簡稱ODE)是未知函数只含有一个自变量的微分方程。
很多科学问题都可以表示为常微分方程,例如根据牛顿第二运动定律,物体在力的作用下的位移 和时间 的关系就可以表示为如下常微分方程:

ODE solver是常微分方程的数值解法工具。它使用数值解法来近似求解常微分方程,得到近似的解。

从输入层 h(0) 开始,我们可以将输出层 h(T ) 定义为这个 ODE 初始值问题在某个时间 T 的解。该值可以由黑盒微分方程求解器计算。
给定z(t0)和f的参数,向前传播求解z(t1)很容易。(只需要一个ODESolve)
但是用反向传播求L 关于 θ 的梯度,怎么求?

第一步是确定损失的梯度如何取决于每个时刻的隐藏状态 z(t)。这个量称为伴
随 a(t) = ∂L /∂z(t) 。它的动态由另一个 ODE 给出,
 (35)
(35)
我们指出了伴随方法和反向传播(等式 38)之间的相似性。类似于反向传播,伴随态的 ODE 需要及时向后求解。我们在最后一次指定为约束点,就是最后一个时间点的loss的梯度,可以得到关于任何时候的隐藏状态,

t为tN的时候,∂f(z(t), t, θ) /∂z(t)的计算方法和其他时间点没有区别,只是把t的值换成tN而已。我们只需要把z(tN)和tN输入到f中,然后用自动微分的方法求出f对z(tN)的偏导数就可以了。
扩展上面的方法,推广可以得到关于 θ 的梯度

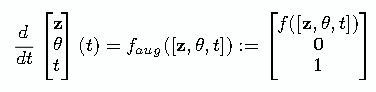

f 的雅可比行列式(指f对它的输入变量的偏导数组成的矩阵)具有以下形式
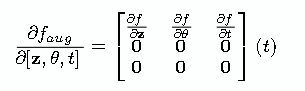 结合(35)
结合(35)


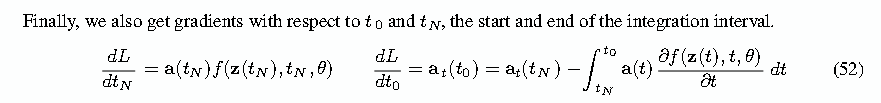


 算法1的目的是计算一个常微分方程初值问题的反向模式导数,也就是损失函数对参数的梯度
算法1的目的是计算一个常微分方程初值问题的反向模式导数,也就是损失函数对参数的梯度







相关文章:

常微分方程ODE和Neural Ordinary Differential Equations
微分方程(英語:Differential equation,DE)是一種數學方程,用來描述某一類函数與其导数之间的关系。微分方程的解是一個符合方程的函數。而在初等数学的代数方程裡,其解是常数值。 常微分方程(英…...
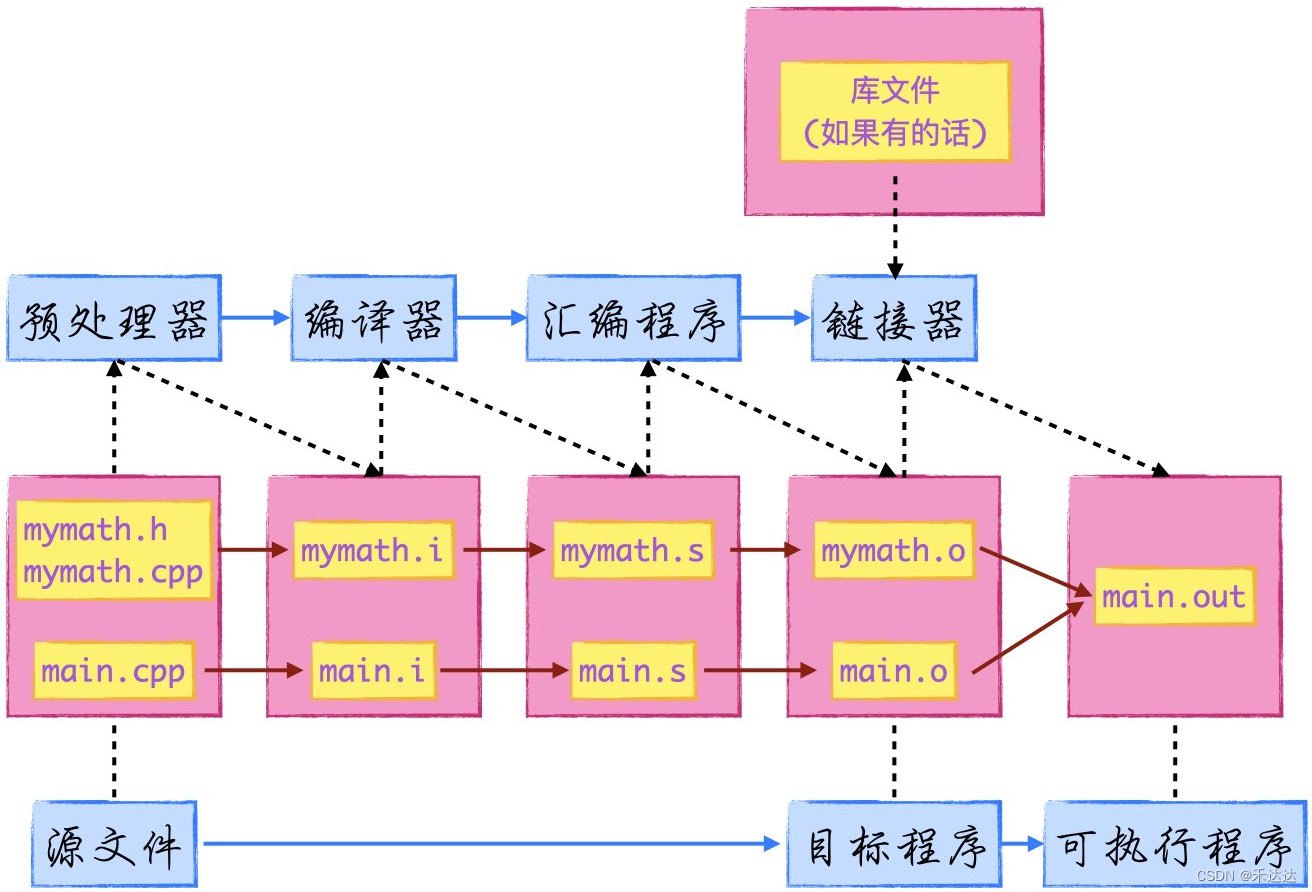
C++ 编译过程(附简单实例)
C 采用分离编译模式,分离编译指的是,一个程序/项目是由若干个源文件共同实现,编译时先把每个源文件单独编译生成目标文件,再将所有目标文件连接起来,形成单一的可执行文件。 C 编译的四个阶段:预处理、编译…...
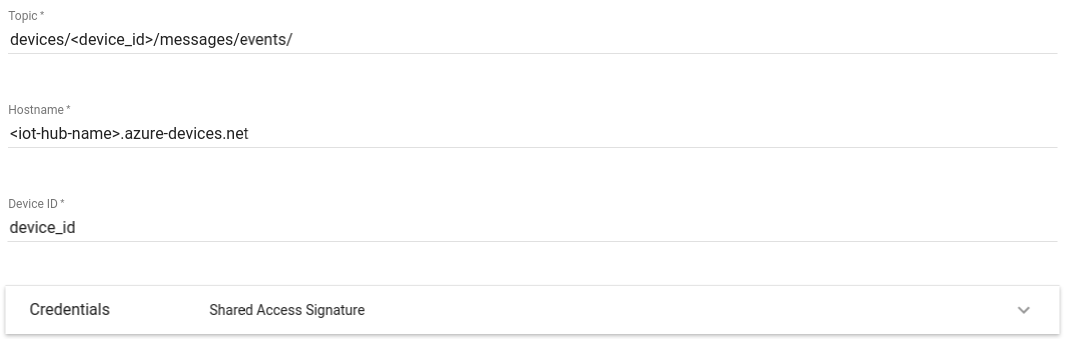
ThingsBoard教程(五四):规则节点解析 Azure IoT Hub Node, RabbitMQ Node
Azure IoT Hub Node Since TB Version 2.5.3 配置 主题 - 获取有关IoT Hub主题的更多信息,请使用以下链接。主机名 - Azure IoT Hub主机名。设备ID - 来自Azure IoT Hub的设备ID。凭据 - Azure IoT Hub连接凭据。可以是共享访问签名或PEM格式证书。Azure IoT Hub支持不同的…...

元素偏移量offset
文章目录 1. offset概述2. offset与style的区别 1. offset概述 offset就是偏移量,我们使用offset系列相关属性可以动态的得到该属性的位置(偏移)、大小等。 element.offsetParent 返回作为该元素带有定位的父级元素,如果父级都没…...
如何让自动化测试框架更自动化?
一、引言 对于大厂的同学来说,接口自动化是个老生常谈的话题了,毕竟每年的MTSC大会议题都已经能佐证了,不是大数据测试,就是AI测试等等(越来越高大上了)。不可否认这些专项的方向是质量智能化发展的方向&…...

无屏幕实现连接树莓派
无屏幕实现连接树莓派 欢迎来到我的博客!今天我将与大家分享如何无需使用屏幕,实现与树莓派的连接。对于那些在树莓派项目中不方便使用屏幕的人来说,这将是一个有用的技巧。 材料清单 在开始之前,让我们先准备好所需的材料&…...
系统启动流程)
【Android】AMS(一)系统启动流程
前言 AMS(Activity Manager Service)即活动管理器服务,是Android系统中的一个核心服务。它主要负责管理应用程序的生命周期,包括启动应用程序、切换应用程序、管理任务栈等。 Android启动流程 Android程序的启动流程可以概括为…...

FineBI6.0基础学习第一课 数据门户
PC端门户使用示例 首先,以管理员身份登录FineBI系统,安装数据门户,安装步骤见官网 新建一个数据门户...
如何部署项目到Tomcat + 第一个Servlet程序
博主简介:想进大厂的打工人博主主页:xyk:所属专栏: JavaEE初阶 目录 文章目录 一、Tomcat 1.1 Tomcat是什么 1.2 下载安装 1.3 部署项目 二、第一个Servlet程序 2.1 Servlet是什么 2.2 创建Maven项目 2.3 引入依赖 2.4 创建目录 2.5 编写类方法 2.6 打包…...
)
牛客刷题(HTML-Day1)
第一题: 1.下列代码在页面中显示的内容为( ) <!DOCTYPE html> <html> <body> <p>hello<q>html</q></p> </body> </html> A hello“html” B hello html C hello“”html D 其他几…...

性能测试如何入门?熬夜7天整理出这一份3000字超全学习指南
赶鸭子上架要我搞性能测试,怎么办? 我第一次真正意义上搞性能测试是在2014年。项目组要求搞性能测试,我之前也没搞过,对服务端也不熟悉。就那么一脸懵逼地开始搞性能。当时我连linux上有哪些能看系统资源的命令都不知道。稀里糊涂…...
信息安全实践1.2(重放攻击)
前言 这个实验是看一本书做的,就是李华峰老师的书——《Metasploit Web 渗透测试实战》,我之前写过一篇Slowloris DoS攻击的博客,也是看这本书写的,总的来说,有用处。这篇博客其实也只是很浅显的去做一下重放攻击。 要…...
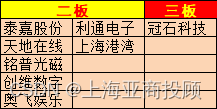
上海亚商投顾:沪指高开高走 地产股迎来久违反弹
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪 三大指数今日高开高走,沪指午后涨近1%,深成指、创业板指涨超1.2%,上证50盘中大…...
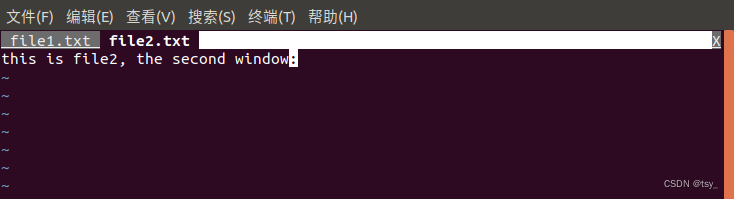
Vim学习笔记【Ch02】
Vim学习笔记 系列笔记链接Ch02 Buffers, Windows, TabsBuffers什么是buffer查看所有bufferbuffer之间的切换删除buffer退出所有窗口 Windows窗口的创建窗口切换快捷键其他快捷键 Tabs什么是tabtab相关命令 window和buffer结合的3D移动小结 系列笔记链接 Ch00,Ch01 …...

《低代码指南》——低代码维格云能源行业解决方案
目录 典型场景介绍: 一、能源资产管理 二、碳核查 三、配电运营 总 结: 从业界实际情况来看,流程建设本身是一个对业务现实进行抽象的过程,这个过程即使不考虑软件开发的门槛,对于很多客户而言也是个涉及较长周期的复杂工作,往往需要咨询专家或专业公司帮助其建设内…...

【自制C++深度学习推理框架】Layer的设计思路
Layer的设计思路 Layer的抽象 如果将深度学习中的所有层分为两类, 那么肯定是"带权重"的层和"不带权重"的层。 基于层的共性,我们定义了一个Layer的基类,提供了一些基本接口,并可以通过继承和多态机制实现不同类型的L…...

Rust每日一练(Leetday0011) 下一排列、有效括号、搜索旋转数组
目录 31. 下一个排列 Next Permutation 🌟🌟 32. 最长有效括号 Longest Valid Parentheses 🌟🌟🌟 33. 搜索旋转排序数组 Search-in-rotated-sorted-array 🌟🌟 🌟 每日一练刷…...

STL --- 五. 函数对象 Function Objects
目录 1、函数对象的定义和作用 2、函数对象的分类和使用 3、std 常用的函数对象 4、函数对象的适配器 5、std 算法和函数对象区别 1、函数对象的定义和作用 STL(Standard Template Library)中的函数对象(Functor)是一种重载…...

Java IO 流操作详解
Java IO 流操作详解 一、简介1. 什么是IO流2. IO流的分类3. IO流的作用 二、Java IO流的输入操作1. 文件输入流2. 字节输入流3. 缓冲输入流4. 对象输入流 三、Java IO流的输出操作1. 文件输出流2. 字节输出流3. 缓冲输出流4. 对象输出流 四、Java IO流的常用方法解析1. 字节读写…...

Halcon 形状匹配参数详解
find_shape_model(Image : : ModelID, AngleStart, AngleExtent, MinScore, NumMatches, MaxOverlap, SubPixel, NumLevels, Greediness : Row, Column, Angle, Score) find_shape_model(Image : : //搜索图像 ModelID, //模板句柄 AngleStart, // 搜索时的起始角度 AngleExte…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
