Java程序设计入门教程--原始类与包装类
包装类
Java语言是一个面向对象的语言,但是Java中的基本数据类型却是不面向对象的,这在实际使用时存在很多的不便。
为了解决这个不足,在设计类时为每个基本数据类型设计了一个对应的类进行代表,这样八个和基本数据类型对应的类统称为包装类(Wrapper Class),有些地方也翻译为封装类或数据类型类。
包装类均位于java.lang包。
包装类和基本数据类型的对应关系如表所示
| 基本数据类型 | 包装类 | 构造方法 |
| boolean | Boolean | Boolean(boolean b)或Boolean(String s) |
| byte | Byte | Byte(byte b) 或Byte(String s) |
| char | Character | Character(char c) |
| short | Short | Short(short s ) 或Short(String s) |
| int | Integer | Integer(int i) 或者Integer(String s) |
| long | Long | Long(long l)或者Long(String s) |
| float | Float | Float(double d)或者Float(float f)或者Float(String s) |
| double | Double | Double(double d)或者Double(String s) |
另外还有两个包装类BigInteger、BigDecimal没有相对应的基本类型,主要应用于高精度的运算,BigInteger 支持任意精度的整数, BigDecimal支持任意精度带小数点的运算。
包装类的功能
包装类属于引用数据类型,具有属性和方法,使用这些方法可以实现很多基本数据类型没有的功能,包装类主要提高以下功能:(1)将基本数据类型包装后,可以当做对象使用;(2)为基本数据类型提供各种转换功能,如将数值转换为字符串,将字符串转换为数值。
有些数据结构如ArrayList,HashMap等不能存放原值类型,这时只能使用其包装类。
基本数据类型和其包装类间的转换(以Integer类为例)
(1)基本类型转换为包装类型: Integer I=new Integer(primitive value);
(2)包装类型转换为基本类型: int a=I.intValue()。
基本类型与包装类型主要异同:
1. 在Java中,一切皆对象,但八大基本类型却不是对象。
2. 声明方式的不同,基本类型无需通过new关键字来创建,而封装类型需new关键字。
3. 存储方式及位置的不同,基本类型是直接存储变量的值保存在堆栈中能高效的存取,封装类型需要通过引用指向实例,具体的实例保存在堆中。
4. 初始值的不同,封装类型的初始值为null,基本类型的的初始值视具体的类型而定,比如int类型的初始值为0,boolean类型为false;
5. 使用方式的不同,比如与集合类合作使用时只能使用包装类型。
相关文章:

Java程序设计入门教程--原始类与包装类
包装类 Java语言是一个面向对象的语言,但是Java中的基本数据类型却是不面向对象的,这在实际使用时存在很多的不便。 为了解决这个不足,在设计类时为每个基本数据类型设计了一个对应的类进行代表,这样八个和基本数据类型对应的类统…...

pip安装python库速度慢、失败及超时报错解决办法
背景: 随着人工智能的不断兴起,python作为最接近人工智能的语言,变得越来越流行,人生苦短,python要学起来。之所以越来用的人喜欢学习python和研究Python,除了python本身便于学些、语法简短、面向对象等特点…...

向量数据库
向量数据库可以做哪些事情 存储和索引向量检索相似向量,还具有过滤功能自动将文档转变成向量,所以会自动化分词、向量化、索引等操作 目前存在的向量数据库: 名称github开源协议chromahttps://github.com/chroma-core/chromaApache 2.0Mil…...
leetcode 11.盛最多水的容器
题目描述 跳转到leetocde题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明ÿ…...

都说00后已经躺平了,但是有一说一,该卷的还是卷啊。
这不,三月份春招我们公司来了个00后,工作没两年,跳槽到我们公司起薪20K,都快接近我了。 后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条件不太好&…...
)
牛客网刷题学习SQL(二)
SQL22 统计每个学校的答过题的用户的平均答题数 描述 运营想要了解每个学校答过题的用户平均答题数量情况,请你取出数据。 用户信息表 user_profile,其中device_id指终端编号(认为每个用户有唯一的一个终端),gender指…...

深蓝学院 C++笔记 先导篇章 - 绪论
一、介绍-老师寄语 为什么选择C? 高性能解决问题 二、C推荐书目 1. 基础 《C Primer》,Stanley B. Lippman 等著,王刚、杨巨峰等译 2. 进阶 《Effective C》,Scott Meyers 著,侯捷译。 《More Effective C》&am…...

R7-19 天梯赛团队总分
“天梯赛”的竞赛题目一共有 15 道,分为 3 个梯级: 基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;题目编号相应为L1-X,X取1,2,3,4,5,6,7,8,分别表示基础级的8道题…...

使用 Kotlin 的 Opt-in (选择加入)功能注解API提示当前非稳定API
前言 之前在给公司项目封装库的时候,领导告诉我封装的漂亮一点,等以后公司发展起来了可能需要把这个库提供给第三方接入使用。 此时,就有这么一个问题:某些功能函数使用条件比较苛刻,直接使用可能会出现意想不到的后…...

webpack配置排除打包
webpack配置排除打包 思路 打包时,不要把类似于element-ui第三方的这些包打进来 从网络上,通过url地址直接引入这些包 操作 (1)先找到 vue.config.js, 添加 externals 项,具体如下: config…...

HNU-操作系统OS-ucoreLab系列-感悟
谨以此片篇,献给熬夜的8个晚上,以及逝去的时光。 感悟: 今天结束了所有的Lab实验(2023.6.3),感慨万千。 喜是这个实验终于结束了,悲是其实有好多地方我都没有理解。 应该指出,由于验收的助教学长学姐们的宽容,HNU实际上在验收这一块的要求还是比较低的。 但是这个…...
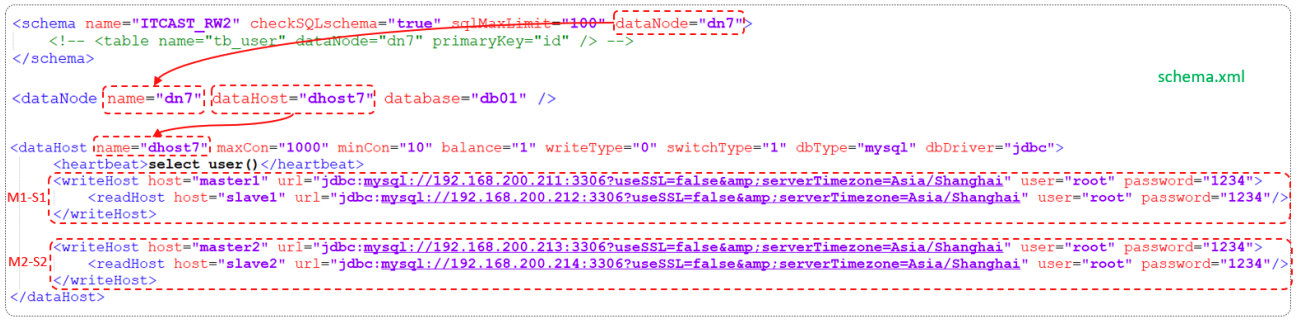
MySQL运维篇(三)
五.读写分离 5.1 介绍 读写分离,简单地说是把对数据库的读和写操作分开,以对应不同的数据库服务器。主数据库提供写操作,从数据库提供读操作,这样能有效地减轻单台数据库的压力。 通过MyCat即可轻易实现上述功能,不仅可以支持MySQL&#x…...

Lecture 2 Text Preprocessing
目录 Some DefinitionsReasons for PreprocessingPreprocessing StepsSentence Segmentation 句子分割Binary Classifier 二元分类器Word Tokenization: English 英文词元标记化Word Tokenization: Chinese 中文词元标记化Word Tokenization: German 德语词元标记化Subword Tok…...
web练习第二周
前言:(博主个人学习笔记,不用看)web练习第二周,仅做出前3题。相比于第一周,难度大幅增加,写题时就算看了wp还是像个无头苍蝇一样到处乱创,大多都是陌生知识点,工具的使用…...
)
LC-1439. 有序矩阵中的第 k 个最小数组和(二分答案、多路归并)
1439. 有序矩阵中的第 k 个最小数组和 难度困难120 给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。 你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。 示例 1:…...

一文1000字从0到1实现Jenkins+Allure+Pytest的持续集成
一、配置 allure 环境变量 1、下载 allure是一个命令行工具,可以去 github 下载最新版:https://github.com/allure-framework/allure2/releases 2、解压到本地 3、配置环境变量 复制路径如:F:\allure-2.13.7\bin 环境变量、Path、添加 F:\…...
)
给一个有序数组生成平衡搜索二叉树(java)
给一个有序数组生成平衡搜索二叉树 给一个有序数组生成平衡搜索二叉树递归生成二叉树专题 给一个有序数组生成平衡搜索二叉树 给定一个有序的数组,用这个数组生成一个平衡搜索二叉树. 这个题还是很简单的,知道什么时平衡搜索二叉树就行了, 左边值小于头节点值,头节点值小于右边…...

【JavaSE】Java基础语法(二十二):包装类
文章目录 1. 基本类型包装类2. Integer类3. 自动拆箱和自动装箱4. int和String类型的相互转换 1. 基本类型包装类 基本类型包装类的作用 将基本数据类型封装成对象的好处在于可以在对象中定义更多的功能方法操作该数据常用的操作之一:用于基本数据类型与字符串之间的…...
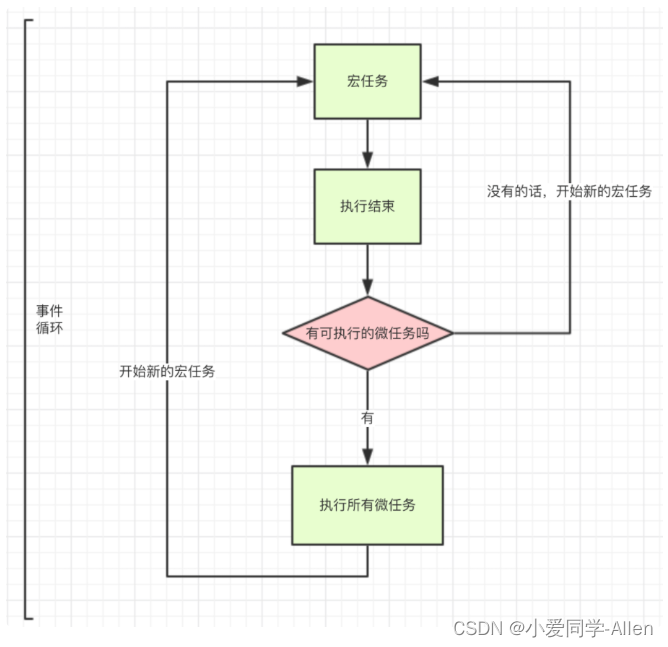
javascript基础十八:说说你对JavaScript中事件循环的理解
一、是什么 JavaScript 在设计之初便是单线程,即指程序运行时,只有一个线程存在,同一时间只能做一件事 为什么要这么设计,跟JavaScript的应用场景有关 JavaScript 初期作为一门浏览器脚本语言,通常用于操作 DOM &#…...

详解js中的浅拷贝与深拷贝
详解js中的浅拷贝与深拷贝 1、前言1.1 栈(stack)和堆(heap)1.2 基本数据类型和引用数据类型1.2.1 概念1.2.2 区别1.2.3 基本类型赋值方式1.2.4 引用类型赋值方式 2、浅拷贝2.1 概念2.2 常见的浅拷贝方法2.2.1 Object.assign()2.2.…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...

【Redis】Redis 的持久化策略
目录 一、RDB 定期备份 1.2 触发方式 1.2.1 手动触发 1.2.2.1 自动触发 RDB 持久化机制的场景 1.2.2.2 检查是否触发 1.2.2.3 线上运维配置 1.3 检索工具 1.4 RDB 备份实现原理 1.5 禁用 RDB 快照 1.6 RDB 优缺点分析 二、AOF 实时备份 2.1 配置文件解析 2.2 开启…...
