恒容容器放气的瞬时流量的计算与合金氢化物放氢流量曲线的计算
有时候,你会遇到一个问题,该问题的描述如下:
你有一个已知体积的容器,设容器体积为V,里面装有一定压力(初始压力)的气体,如空气或氢气等,设初始压力为1MPa,容器出口连接着一个阀门开关,开关后面接1/4in.的钢管,钢管出口即为气体出口。当阀门瞬间全开时,气体出口的瞬时流量值随时间变化到底是怎么样的呢?
该问题相当于在不考虑管壁与管长对气体产生粘滞阻力的影响下,已知气体管道直径d,即管道横截面积
,已知管子进口静压为
,已知管子出口静压为
,即一个大气压,同时知道进口气体总温
为323K,求出口瞬时流量随时间
的变化关系和曲线。
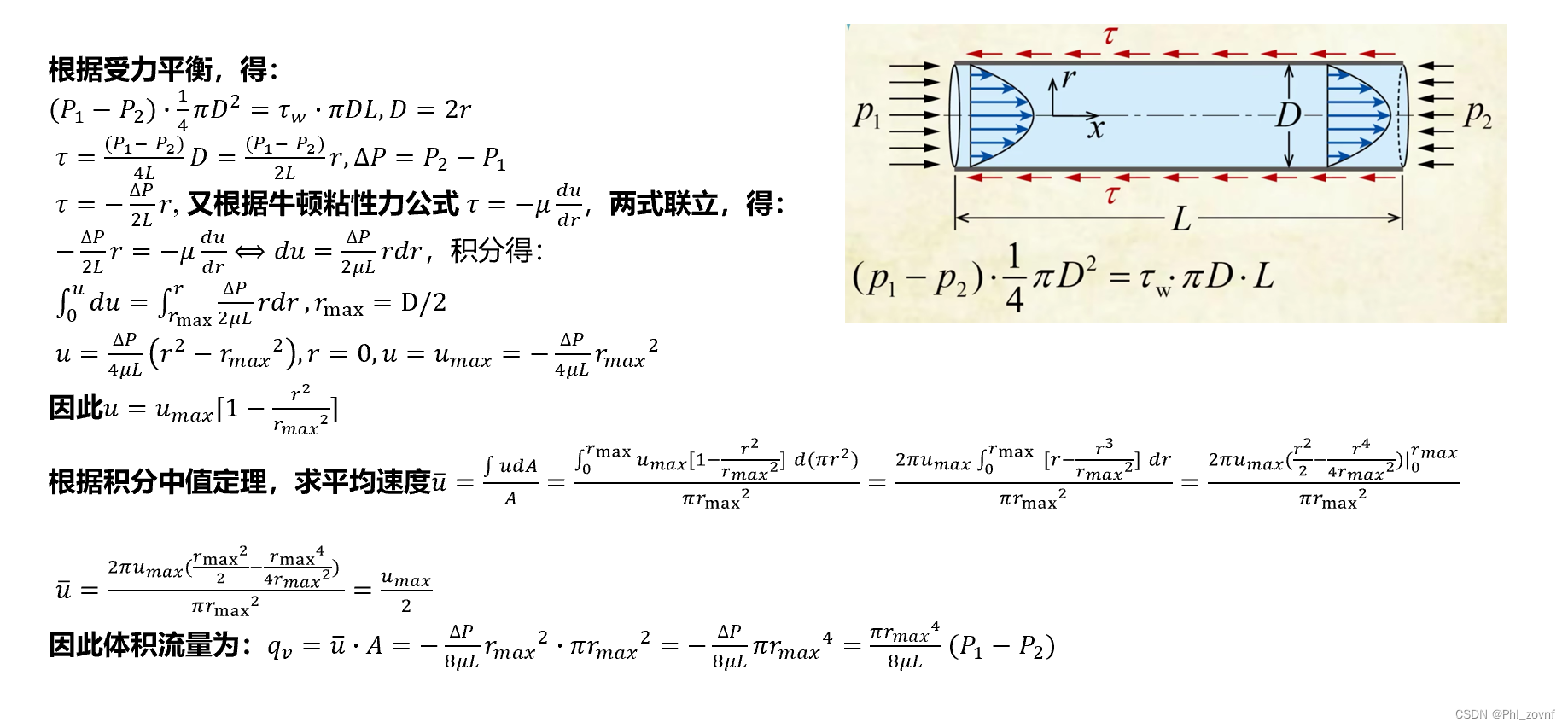
1. 第一种方法:根据哈根泊谡叶方程
利用理想气体方程:和哈根泊谡叶关系式:
,
表示的是体积流量,单位为
,
是管子的半径,
是流体的动力黏度,单位是
,
是管子的长度,压强
的单位为
。两个方程联立,可得
,
,利用该关系式,得到
随时间
的关系如下图所示,为一指数函数形式,而且可以通过积分,得到积分总流量为
,根据
,可见积分与差分得出的总流量非常接近。
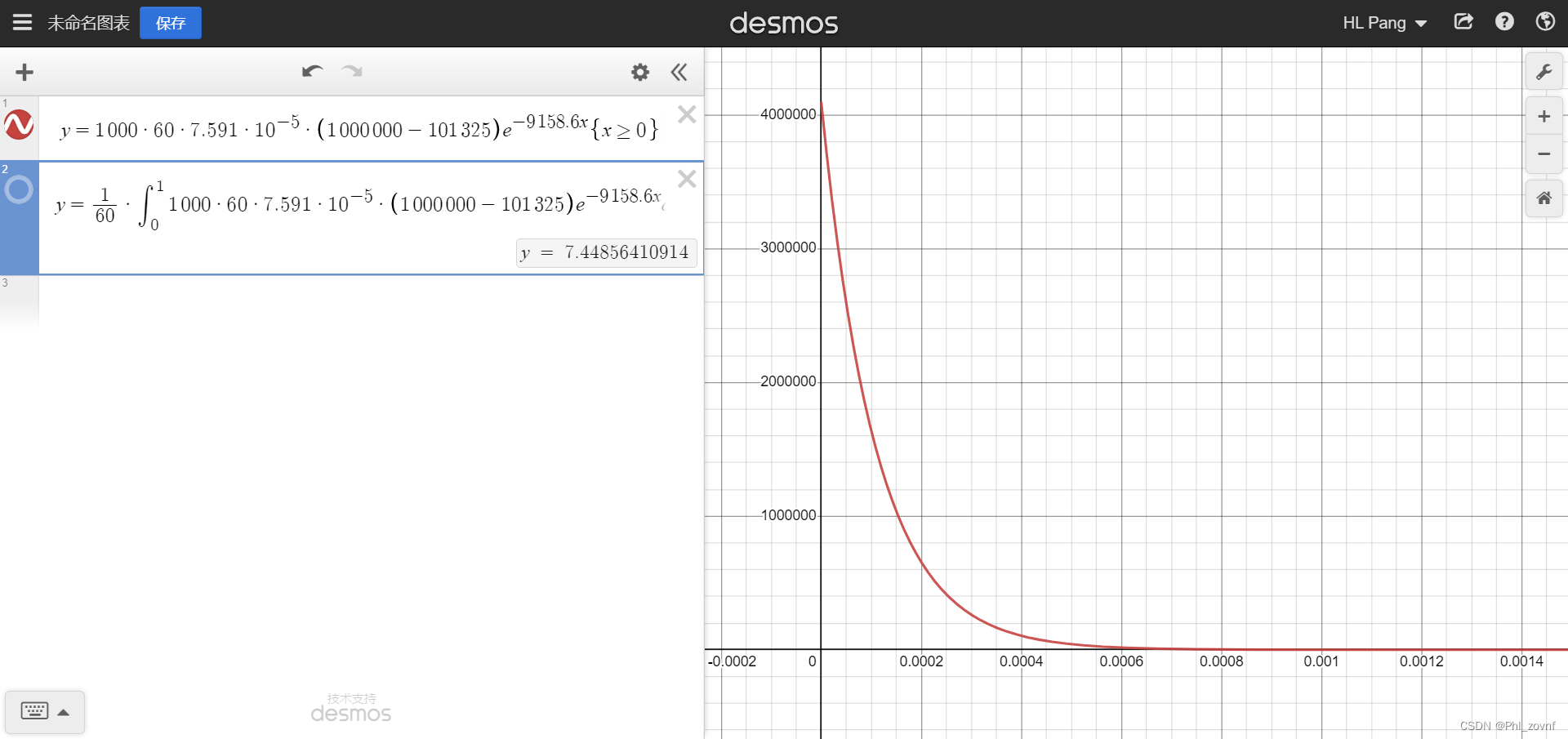
 不过根据推导,一开始的瞬时流量值非常离谱,可以去到
不过根据推导,一开始的瞬时流量值非常离谱,可以去到,根据
,
可以知道出口流体平均速度
,光速是
,出口速度已经达到
倍的光速,也超过空气声速
,应该会听到音爆?实际好像没有发生这样的现象,但出口处确实会产生挺大的声音。
附:关于哈根泊谡叶关系式的推导,见下图。
2. 第二种方法:根据气体动力学推算
假设排气过程与气体管道壁面的换热忽略不计,即壁面是绝热的,气体流体是一个准稳态问题,排气口相当于是收缩,没有扩张,根据气体动力学可知,出口气体流速只能加速到1马赫数,即。根据总静温关系式
,得知
。再根据马赫数定义式
,这里
是气体比热容比,定义为定压比热
与定容比热
之比,变换后有
,
,
,比气体常数
为:
,得到氢气气体流速
。
根据,
,
,
,
,
,
为一个大气压。在
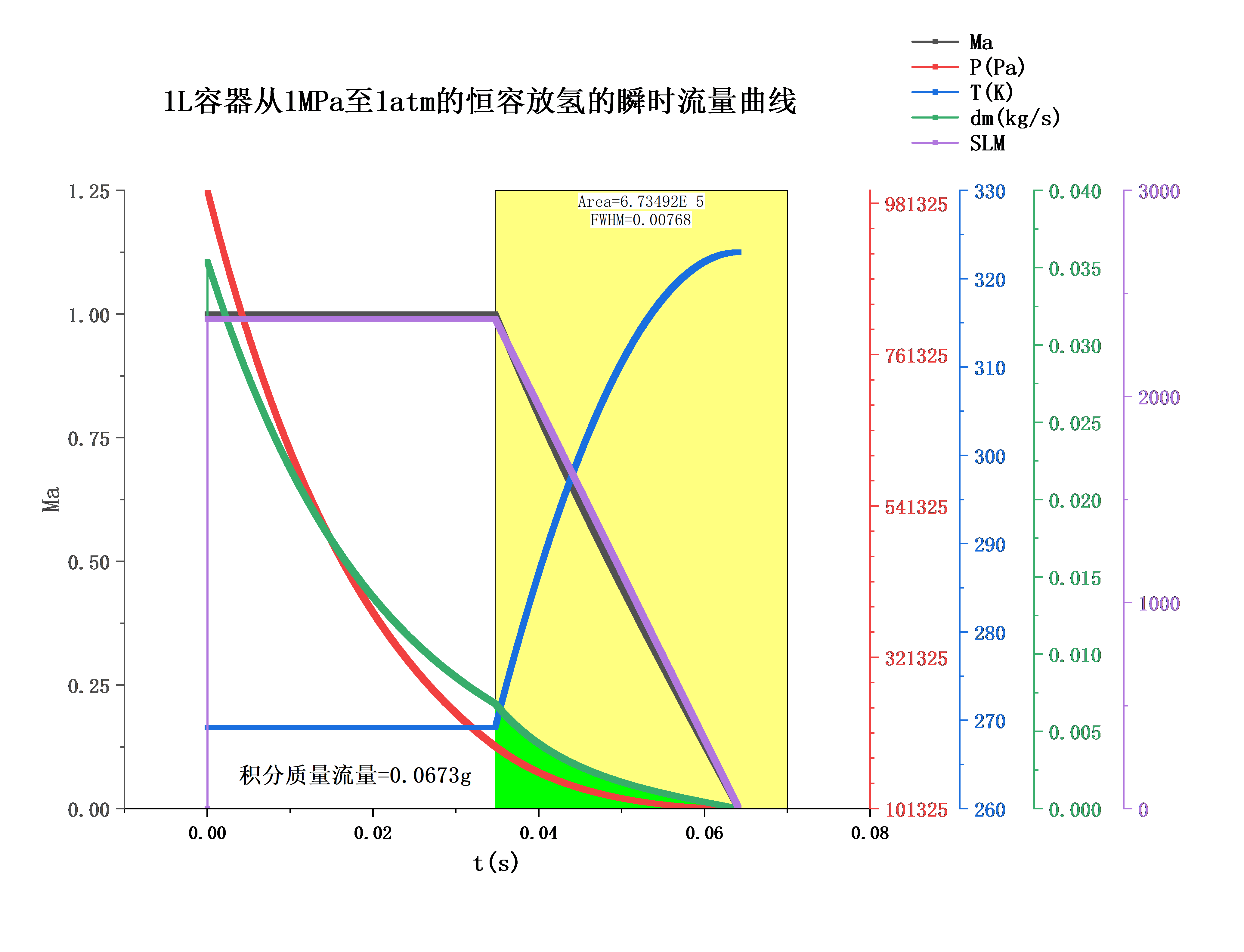
的壅塞流阶段,可解得
。这阶段,理解为流速
不变,
变化导致的
变化,瞬时质量流量也会随之变化,但体积流量
不变。如下图所示,绿色曲线是瞬时流量,紫色曲线是体积流量,绿色部分面积是积分得到的总质量流量,通过积分得到壅塞流下的总质量流量为
,换算成密度为
的体积流量为
。

后面非壅塞流状态下的亚声速流,原则上也是利用,
,
,
,
,这5个式子得到
的关系,我用欧拉法获得解析解的近似值,得到后续的流量曲线,具体步骤是,知道压力初始条件
,初始瞬时流量为
,也就是等于壅塞流状态下最后一刻时间的流量,然后利用瞬时流量乘以时间小量,得到
,再利用关系式
,得到
的变化量,然后计算马赫数
、速度
,温度
等参数,不断进行迭代计算,当
时结束迭代。如下图中绿色的质量流量曲线和紫色的体积流量曲线,通过积分面积算得亚声速流下总质量流量为
,换算成密度为
的体积流量为
,因此放氢整个过程总质量流量为
,与
算出来的基本一致。整个过程的总体积流量为
。

具体更可靠的计算,请读者参考GB/T 14513.3-2020中的方法。
在经典的合金氢化物动力学描述中,有一种是用JMAK方程来描述和拟合合金的吸放氢过程,方程很简洁:
,其中
是反应程度或者百分比,表示合金氢化物吸氢或者放氢的程度,
是该合金吸氢或放氢的一种特征常数,经常是通过实验测得动力学曲线后进行拟合得到,
是时间。该方程的曲线形状如下图所示。
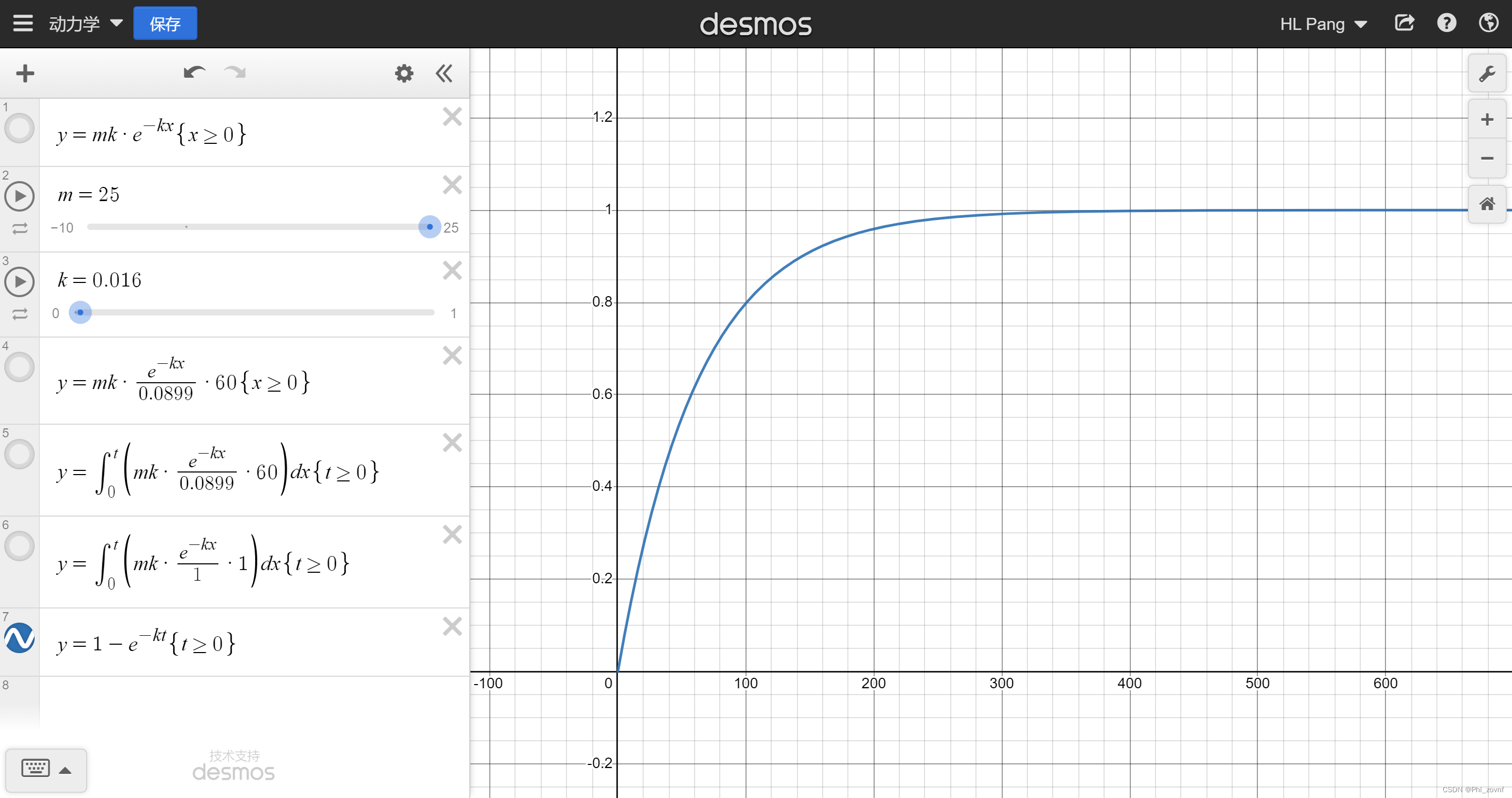
由于
是反应程度,因此假设合金最终能放出
标升的氢气,则方程可变为
,该方程对时间
进行求导,可得
,该曲线即为瞬时体积流量曲线,其曲线形状如下图,
越大,初始瞬时流量越大,放氢时间越短。
实测可取值0.00005~0.05之间。
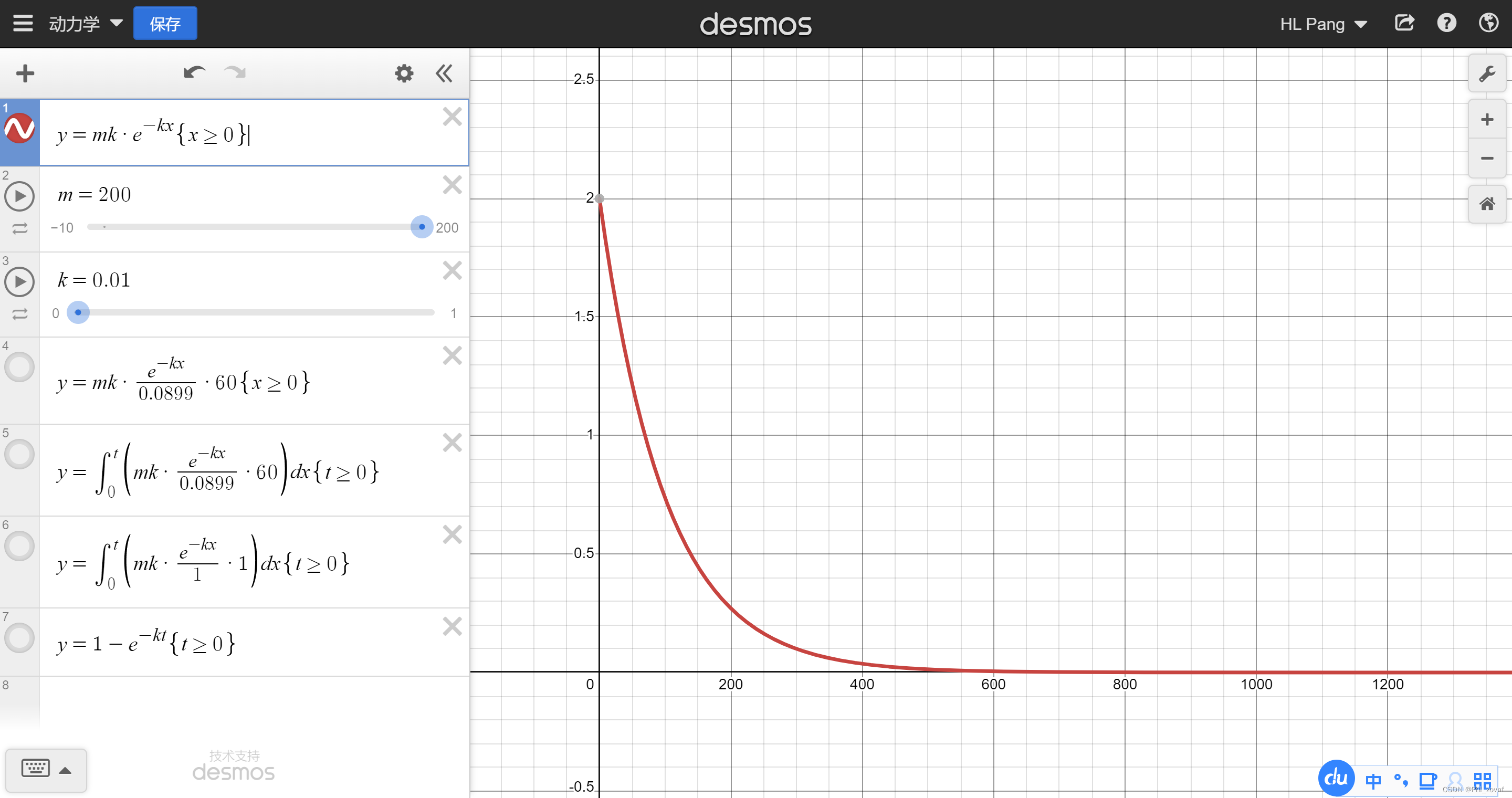
合金放氢后,使得容器内压力
上升,合金动力学方程
,
是放氢总质量,在这里,我假设
,利用上述5个公式和数值计算,可以知道在壅塞流状态下,合金动力学方程中,每
放出的氢,导致容器内上升的压力只有
左右,结合上述气体动力学算出来的瞬时流量,可认为这阶段合金放氢所带来的压力影响可忽略。就算是非壅塞流阶段,由于合金总储氢量
比较小,因此也是接近非壅塞流末段,合金放氢对瞬时流量的影响才开始凸现,此时合金单独放氢的动力学曲线此时可以接驳到瞬时流量曲线上去。也就是说,瞬时流量曲线前部分是气体动力学算出来的流量曲线,到一定压力时,合金放氢动力学曲线就跟前者流量曲线接上即可。
我大概算了下,通过数值计算的瞬时流量如下图,10s的瞬时流量为26.97SLM(L/min),20s的瞬时流量为22.08SLM,30s的瞬时流量为18.08SLM,50s的瞬时流量为12.12SLM,100s的瞬时流量为4.46SLM,
算出来10s的瞬时流量为26.06SLM,20s的瞬时流量为21.31SLM,30s的瞬时流量为17.45SLM,50s的瞬时流量为11.69SLM,100s的瞬时流量为4.30SLM。两者算出的差距是有,但不算特别大,可接受。
相关文章:

恒容容器放气的瞬时流量的计算与合金氢化物放氢流量曲线的计算
有时候,你会遇到一个问题,该问题的描述如下: 你有一个已知体积的容器,设容器体积为V,里面装有一定压力(初始压力)的气体,如空气或氢气等,设初始压力为1MPa,容器出口连接着一个阀门开…...

网络编程_UDP通信
网络编程_UDP通信 1. TCP与UDP2. 使用UDP通信3. sendto与recvfrom、recv4.实例实例1: 服务器接收、客户端发送实例2:服务器收发、客户方发送、接收。1. TCP与UDP 当使用网络套接字通信时, 套接字的“域”都取AF_INET; 套接字的type: SOCK_STREAM 此时,默认使用TCP协议进行…...
windows修改Pycharm的右键打开方式
title: windows中open floder as Pycharm太长了怎么修改 date: 2023-06-04 author: IoT_H2 tags: windows系统问题 categories: Markdown 问题描述: Pycharm这一栏这么长,长的我实在是很难受,事实上Jetbrains家的软件都是这个鸟模样 导…...
函数(二))
Python入门(十四)函数(二)
函数(二) 1.传递实参1.1 位置实参1.2 关键字实参1.3 默认值 作者:xiou 1.传递实参 函数定义中可能包含多个形参,因此函数调用中也可能包含多个实参。向函数传递实参的方式很多:可使用位置实参,这要求实参…...

Allure测试报告定制全攻略,优化你的Web自动化测试框架!
目录 前言: 1. Allure测试报告简介 2. Web自动化测试框架简介 3. 封装Web自动化框架 3.1 安装Selenium 3.2 封装Selenium 3.3 定制Allure测试报告 3.3.1 适配翻译插件 3.3.2 定制测试报告样式 4. 示例代码 5. 总结 前言: 随着现在Web应用的普…...

推荐系统算法详解
文章目录 基于人口统计学的推荐算法用户画像 基于内容的推荐算法相似度计算基于内容推荐系统的高层次结构特征工程数值型特征处理类别特征处理时间型特征处理统计型特征处理 推荐系统常见反馈数据基于UGC的推荐TF-IDFTF-IDF算法示例1. 引入依赖2. 定义数据和预处理3. 进行词数统…...
企业网站架构部署与优化之LAMP
LAMP LAMP概述1、各组件的主要作用2、各组件安装顺序 编译安装Apache http服务编译安装MySQL服务编译安装PHP解析环境安装论坛 LAMP概述 LAMP架构是目前成熟的企业网站应用模式之一,指的是协同工作的一整套系统和相关软件,能够提供静态和动态Web站点服务…...
攻防世界安卓逆向练习
文章目录 一.easy-so1. jadx分析程序逻辑2. ida查看so文件3. 解题脚本: 二.ezjni1. 程序逻辑分析2. 解题脚本: 三.easyjava1. 主函数逻辑2. getIndex函数3. getChar函数4.解题脚本 四.APK逆向1.程序逻辑分析2.解题脚本3.动态调试 Android2.0app3 一.easy-so 1. jadx分析程序逻…...
)
自然语言处理从入门到应用——自然语言处理的语言模型(Language Model,LM)
分类目录:《自然语言处理从入门到应用》总目录 语言模型(Language Model,LM)(也称统计语言模型)是描述自然语言概率分布的模型,是一个非常基础和重要的自然语言处理任务。利用语言模型ÿ…...
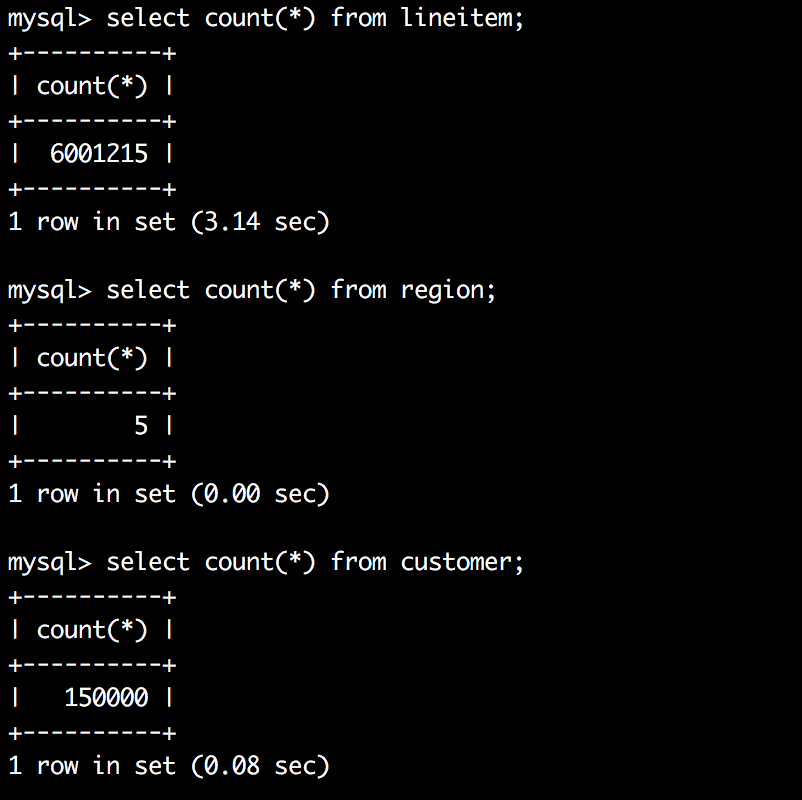
【MySql】InnoDB一棵B+树可以存放多少行数据?
文章目录 背景一、怎么得到InnoDB主键索引B树的高度?二、小结三、最后回顾一道面试题总结参考资料 背景 InnoDB一棵B树可以存放多少行数据?这个问题的简单回答是:约2千万。为什么是这么多呢?因为这是可以算出来的,要搞…...
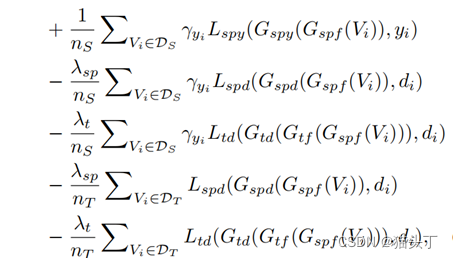
【综述】视频无监督域自适应(VUDA)的小综述
【综述】视频无监督域自适应(VUDA)的小综述 一篇小综述,大家看个乐子就好,参考文献来自于一篇综述性论文 完整PPT已经上传资源:https://download.csdn.net/download/weixin_46570668/87848901?spm1001.2014.3001.550…...

《深入理解计算机系统(CSAPP)》第9章虚拟内存 - 学习笔记
写在前面的话:此系列文章为笔者学习CSAPP时的个人笔记,分享出来与大家学习交流,目录大体与《深入理解计算机系统》书本一致。因是初次预习时写的笔记,在复习回看时发现部分内容存在一些小问题,因时间紧张来不及再次整理…...

信息论与编码 SCUEC DDDD 期末复习
1.证明熵的可加性 2.假设一帧视频图像可以认为是由3*10的五次方个像素组成(每像素均独立变化),如果每个像素可取128个不同的等概率亮度表示。请计算出每帧图像含多少信息量?若有一口述者在约12000个汉字的字汇中选400个字来口述此…...
windows安装python开发环境
最近因工作需要,要学习一下python,所以先安装一下python的开发环境,比较简单 下载和安装Python 首先,在浏览器中打开Python的官方网站(https://www.python.org/downloads/) 然后,从该网站下载与你的操…...

java idea常用的快捷方式
文章目录 java idea常用的快捷方式快速复制选多行改变代码格式化 快速代码编辑psvmsout5.forarr.for快速死循环快速补全代码当方法还没创建的时候抽取具有一定功能的代码变成方法 java idea常用的快捷方式 快速复制 c t r l d \color{red}{ctrld} ctrld 选多行改变 A l t 鼠…...

lwIP 开发指南
目录 lwIP 初探TCP/IP 协议栈是什么TCP/IP 协议栈架构TCP/IP 协议栈的封包和拆包 lwIP 简介lwIP 源码下载lwIP 文件说明 MAC 内核简介PHY 芯片介绍YT8512C 简介LAN8720A 简介 以太网接入MCU 方案软件TCP/IP 协议栈以太网接入方案硬件TCP/IP 协议栈以太网接入方案 lwIP 无操作系…...

RabbitMQ消息属性详解
content-type属性 如同各种标准化的HTTP规范,content-type传输消息体的MIME类型。例如,如果你的应用程序正在发送JSON序列化的数据值,那么将content-type属性设置为application/json将允许尚待开发的消费者应用程序在收到消息时检查消息类型…...

shader 混合模式
在所有着色器执行完毕,所有纹理都被应用,所有像素准备被呈现到屏幕之后,使用Blend命令来操作这些像素进行混合。 3.2 blend的语法 BlendOff:关闭blend混合(默认值) BlendSrcFactor DstFactor :配置并启动混…...

【大数据工具】Hive 安装
Hive 环境搭建与基本使用 Hive 安装包下载地址:https://dlcdn.apache.org/hive/ 注:安装 Hive 前要先安装好 MySQL 1. MySQL 安装 MySQL 安装包下载地址:https://dev.mysql.com/downloads/mysql/archives/community/MySQL%20::%20Downloa…...

Android9.0 iptables用INetd实现app某个时间段禁止上网的功能实现
1.前言 在9.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置app某个时间段禁止上网的功能,liunx中iptables命令也是比较重要的,接下来就来在INetd这块实现app某个时间段禁止上网的的相关功能,就是在系统中只能允许某个app某个时间段禁止上网,就是…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...