基于霍夫变换的航迹起始算法研究(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
一、设计内容
利用Hough变换处理量测得到的含杂波的二维坐标,解决多目标航迹起始问题。使用Matlab进行仿真,用离散点绘制原始数据,用连线绘制处理结果。
二、主要技术指标
1、掌握标准Hough变换检测直线的基本原理,以及一些改进的Hough变换算法。
2、用Matlab实现Hough变换算法,并绘制处理结果。
航迹起始是航迹处理中的首要问题,在各种航迹处理的情况下都存在,对于多目标航迹处理来说,航迹起始是第一步,是进行航迹跟踪的基础。 由于被探测目标一般都是由远到近的出现在搜索雷达的有效探测范围内的,在航迹起始时,目标一般距离雷达较远,此时雷达分辨力低、测量精度差,加之真假目标的出现无真正的统计规律,因此在搜索雷达数据处理技术中,航迹起始问题是一个难题。 现有的航迹起始算法可分为顺序处理技术和批处理技术两大类。通常,顺序数据处理技术适用于弱杂波环境中的航迹起始,主要包括启发式规则方法和基于逻辑方法;批处理技术则更适用于强杂波环境,主要包括Hough变换等方法。基于逻辑的方法在虚警概率比较低的情况下,起始航迹的效果比较好,但在复杂环境下虚假航迹比较多;Hough变换法则适用于强杂波背景下航迹成直线的环境,但是Hough变换法通常需要多次的扫描才能较好地起始航迹,且计算量大不符合工程应用的需要。
低信噪比、低信杂比下的航迹起始是多目标航迹起始的关键问题。Hough变换具有对局部缺损的不敏感性、对随机噪声的鲁棒性以及适于并行处理、实时应用等特点,特别史和解决多目标航迹起始问题。本文对Hough变换航迹起始算法进行了研究,主要工作如下:
1.概述了主要的航迹起始方法,介绍了Hough变换基本原理、Hough变换的特点,指出了Hough变换在航迹起始中存在的问题。
2.研究与分析了标准Hough变换、修正Hough变换和序列Hough变换三种典型航迹起始算法。通过仿真分析,总结出每种算法的适用环境。
Hough变换用于航迹起始具有以下特点:
(1)将量测空间中的检测问题转换到参数空间进行,具有很强的抗干扰能力,对随机噪声具有一定的鲁棒性;
(2)量测中的每一个点都参加“投票”,所以它特别适合并行处理;
(3)一种变换方程只对某一种特定的曲线进行检测,针对性强;
(4)不受空间和曲线形状的影响:广义Hough变换可以检测任意形状的曲线,三维空间Hough变换可以检测空间曲线。
Hough变换用于航迹起始具有以下优点:
(1)Hough变换可以检测任意已知形状的曲线,从而能够起始某类特定航迹,作为先验信息,特定航迹的选定提高了信号相干累积的效率,避免了大量杂波引起的虚假航迹问题;
(2)Hough变换不要求曲线连续或可导,并且对局部缺损和随机噪声鲁棒,适于低检测率和低量测精度下的起始;
(3)Hough变换用于航迹起始不需要目标状态初值,可实现全自动起始。
本文通过大量仿真实验体会到Hough变换航迹起始算法存在若干问题,严重地影响这航迹起始的性能,具体体现在:
(1)标准Hough变换的计算量庞大,并且需要很大的存储空间,在低信噪比环境下表现得特别明显,延长了航迹起始时间,达不到快速性起始的要求。
(2)Hough变换航迹起始算法在提取航迹参数时一般使用阈值法,这就不可避免的出现航迹簇拥现象,即一个目标产生了参数近似的多条轨迹。如何选择峰值提取方法既能准确地提取峰值,同时又能有效地解决航迹簇拥现象,是亟待解决的问题。
(3)Hough变换航迹起始算法应用于工程实际带来了诸多问题,如:实际系统中涉及参数众多,如何对这些参数进行全面有效地利用,是急需解决地问题;针对不同地起始环境应该研究不同地专用算法与之相匹配;实际系统中,很多参数地选取都不能由理论公式推导得出,而要通过大量得仿真实验得出。
📚2 运行结果
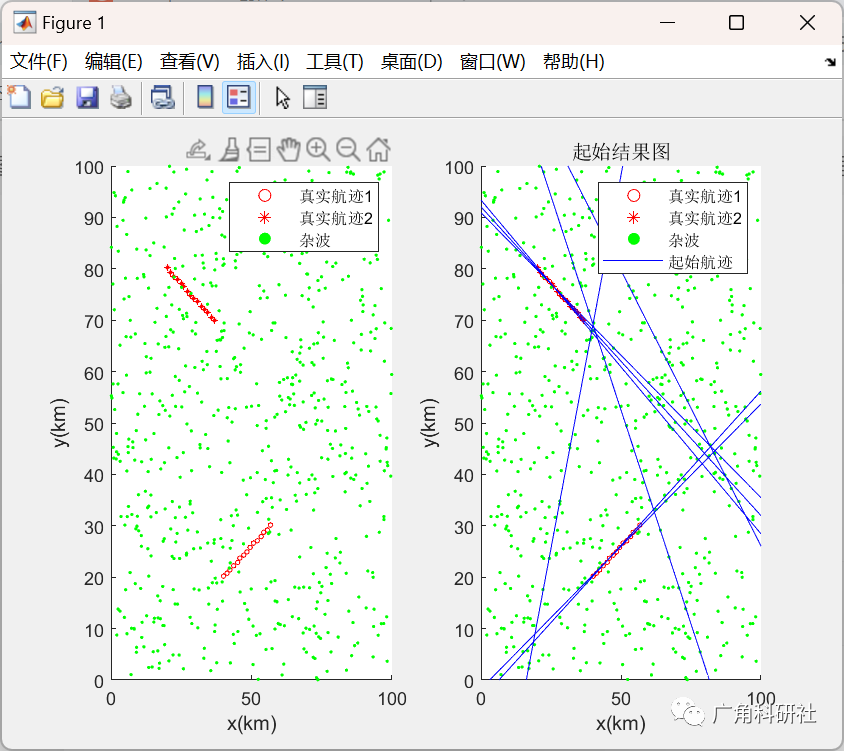
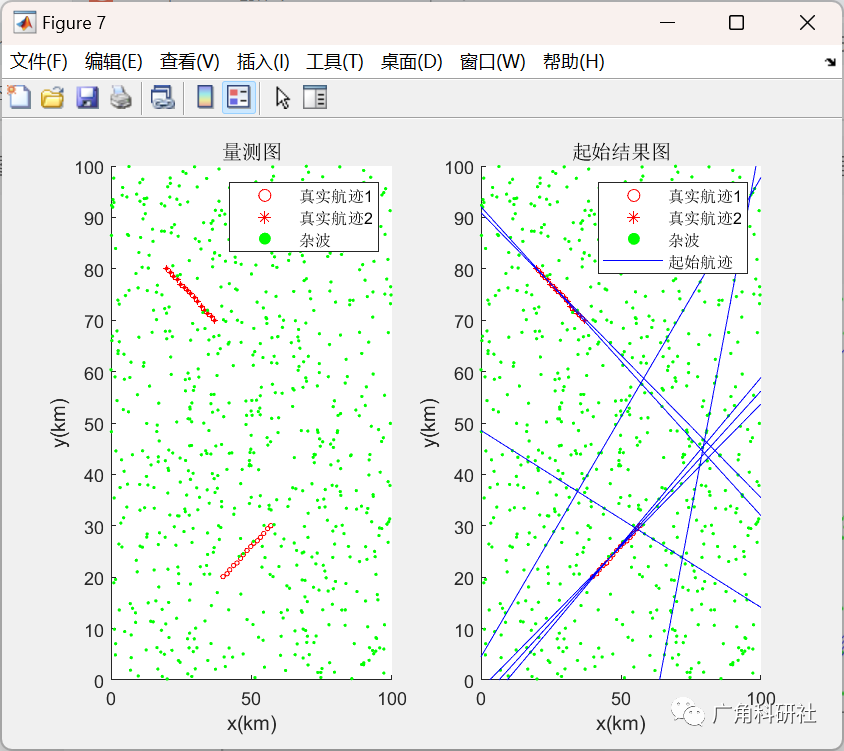
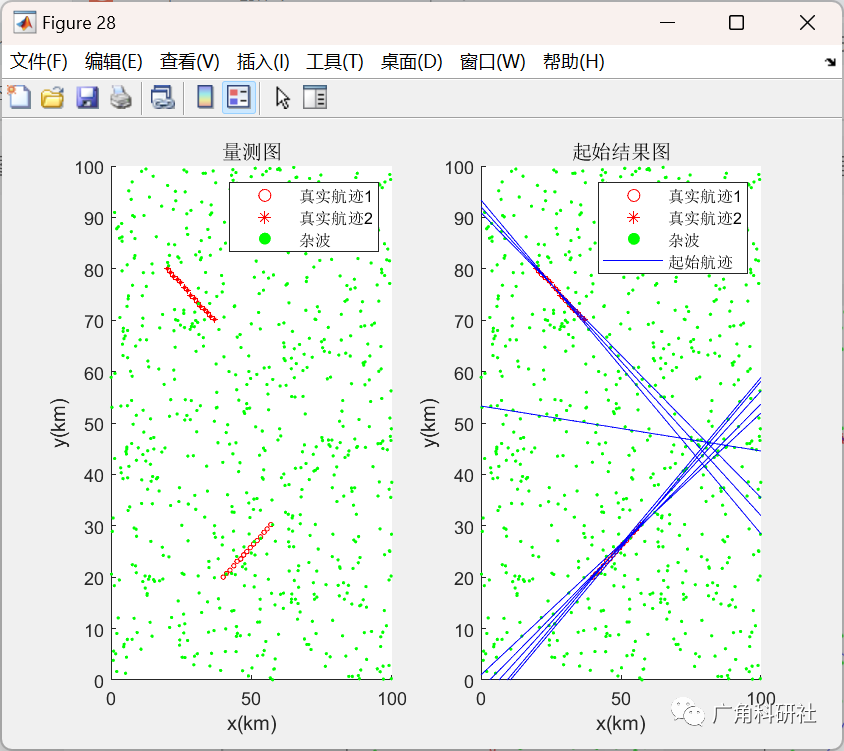
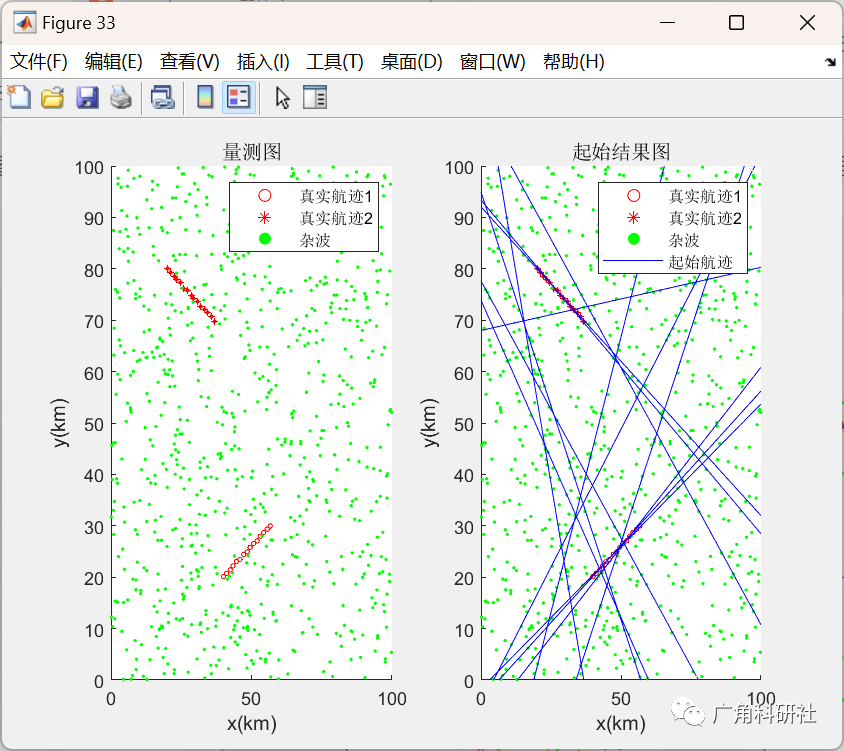

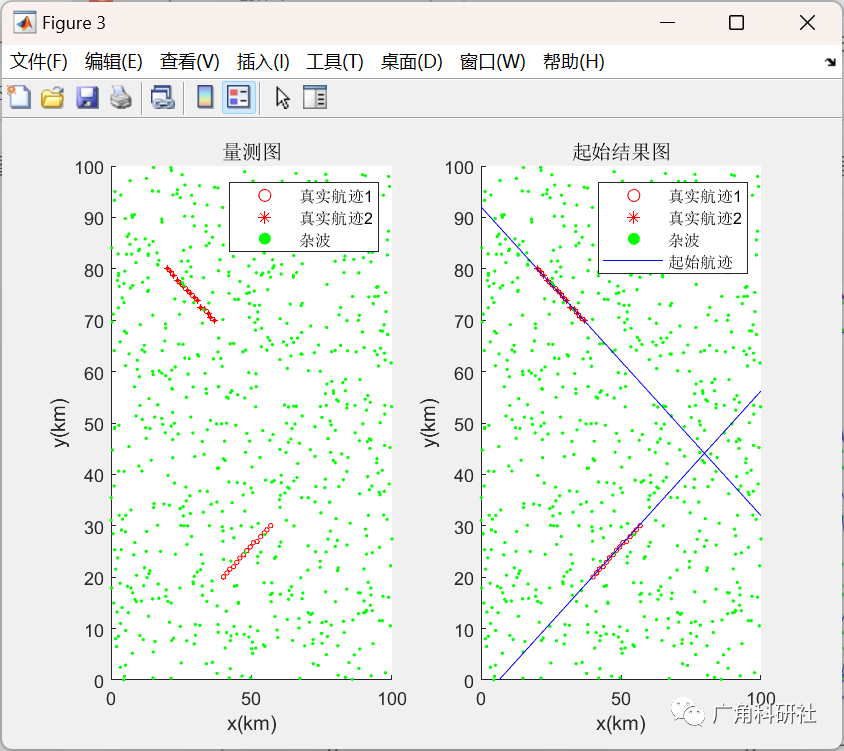
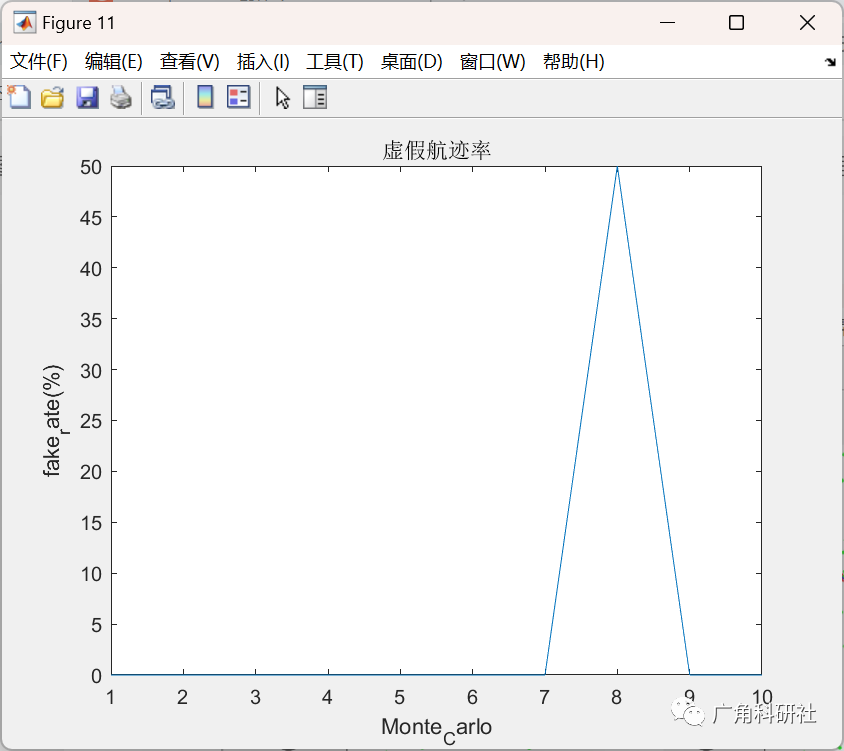
主函数部分代码:
%标准Hough变换 %Author:Shen Baoyin %Time:2018/8/1 close all clear all target=2;%目标数 n=15;%起始拍数 k=90;%sig分的个数 m=500;%p分的个数 Monte_Carlo=100;%Monte_Carlo仿真次数 L=150;%雷达量测距离 Pd=1;%检测概率 %目标起始坐标及速度 x1=40;y1=20;vx1=0.3;vy1=0.18;%单位km,km/s x2=20;y2=80;vx2=0.3;vy2=-0.18; Ts=4;%采样周期,单位s success=zeros(Monte_Carlo,target);%目标航迹成功起始矩阵 fake(1:Monte_Carlo)=0;%目标航迹虚假起始矩阵 track_number(1:Monte_Carlo)=0;%总航迹起始数 N=0:n-1; X1_init=x1+Ts*N*vx1;%真实航迹1 Y1_init=y1+Ts*N*vy1; Y1_0=y1-vy1*x1/vx1; offset(1)=Y1_0*cos(atan(abs(vy1)/abs(vx1)));%航迹1真实垂距 X2_init=x2+Ts*N*vx2;%真实航迹2 Y2_init=y2+Ts*N*vy2; Y2_0=y2-vy2*x2/vx2; offset(2)=Y2_0*cos(atan(abs(vy2)/abs(vx2)));%航迹2真实垂距 Np=1:k; dNp=pi/k;%参数空间角度间隔 angle=(Np-1/2)*dNp; dMp=6*0.1;%%参数空间垂距间隔 for monte=1:Monte_Carloclear R Rn A0 P0 R X_za Y_za noisex noiseyR = poissrnd(50,1,n);%每拍杂波个数,服从泊松分布Rn=R(1);X_za=unifrnd (0, 100, 1, R(1));%随机产生(x,y)坐标,服从0-100的均匀分布Y_za=unifrnd (0, 100, 1, R(1));for i=2:nX_za(Rn+1:Rn+R(i))=unifrnd (0, 100, 1, R(i));Y_za(Rn+1:Rn+R(i))=unifrnd (0, 100, 1, R(i));Rn=Rn+R(i);end noisex=normrnd(0,0.1,1,n);%x量测噪声noisey=normrnd(0,0.1,1,n); X1=X1_init+noisex;X2=X2_init+noisex;%实际量测Y1=Y1_init+noisey;Y2=Y2_init+noisey; A=zeros(k,2*m);%积累矩阵 %航迹1 Hough变换for i=1:nfor j=1:kP(i,j)=X1(i)*cos(angle(j))+Y1(i)*sin(angle(j));endend%航迹2 Hough变换for i=(n+1):(2*n)for j=1:kP(i,j)=X2(i-n)*cos(angle(j))+Y2(i-n)*sin(angle(j));endend %杂波的Hough变换for i=2*n+1:(2*n+Rn)for j=1:kP(i,j)=X_za(i-2*n)*cos(angle(j))+Y_za(i-2*n)*sin(angle(j));endend %对积累矩阵投票for i=1:kfor j=1:2*ma=-L+(j-1)*dMp;b=-L+j*dMp;for h=1:2*n+Rnif (P(h,i)>=a && P(h,i)<b) A(i,j)=A(i,j)+1;endendendend
🎉3 参考文献
[1]高国琴,李明.基于K-means算法的温室移动机器人导航路径识别[J].农业工程学报,2014,30(07):25-33.
部分理论引用网络文献,若有侵权联系博主删除。
相关文章:

基于霍夫变换的航迹起始算法研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 一、设计内容 利用Hough变换处理量测得到的含杂波的二维坐标,解决多目标航迹起始问题。使用Matlab进行仿真&#x…...
快速分割成8列并按顺序排列)
如何使用Excel公式将(d:1,a:4,c:2,b:3)快速分割成8列并按顺序排列
Excel是一款功能强大的电子表格软件,可以帮助我们处理各种数据。在处理数据时,有时候需要将一列数据按照特定的格式进行分割和重新排列。本文将介绍如何使用Excel公式将"(d:1,a:4,c:2,b:3)"快速分割成8列,并按照指定顺序排列为&quo…...

遥控泊车系统技术规范
目 录 1. 版本履历... 3 2. 文档使用范围... 3 3. 术语缩写... 3 4. 系统架构... 4 5. 功能需求... 4 5.1 功能清单... 4 6.2 功能关系描述(如有)... 4 5.3 功能1. 4 5.3.1 功能总体状态动态说…...

qt 线程状态机实现并发自动任务
一、状态机类 头文件 MyStateMachine.h#ifndef MYSTATEMACHINE_H #define MYSTATEMACHINE_H#include <QStateMachine> #include "ActionTask.h" #include...

社交机器人培育
论文: 自我繁殖的假新闻:机器人和人工智能使印度冲突地区的社会两极分化永久化 Self-Breeding Fake News: Bots and Artificial Intelligence Perpetuate Social Polarization in India’s Conflict Zones 论文链接:https://jps.library.ut…...
CUnit在ARM平台上的离线搭建(让CUnit编译安装成功之后的可执行文件.so变成ARM下的—ARM aarch64)(实用篇)
前言:1 CUint-2.1-3.tar.bz2压缩安装包下载并解压2 进入CUint-2.1-3目录并且通过指令./bootstrap*产生configure *执行文件3 执行./configure*命令4 make编译5 make install 安装 前言: 在X86架构上的Linux操作系统上面进行cmake编译(Cyclon…...
整数序列(山东大学考研机试题)
水仙花数(中南考研机试题) 链接:3644. 水仙花数 - AcWing题库 /* 暴力枚举罢了 */ #include<iostream> using namespace std; const int N1e3100; int book[N]; int pow3(int k){return k*k*k; } int main() {int m,n;for(int i100;i<999;i){int t1,t2,t3;t1 i%10;t…...
k8s集群安装
目录 一 主机准备 1.1 设备配置 ⚠️注意1 ⚠️注意2 1.2 环境准备 1.3docker安装 二 安装kubeadm、kubectl、kubelet 2.1 添加镜像源 2.2 安装 三 master节点部署 四 node节点加入集群 五 CNI网络插件calico 六 其他节点使用kubectl 1.拷贝文件 2.添加到环境变量…...

【webrtc】ProcessThreadAttached
RegisterModule 调用所在的线程指针传递给ProcessThreadAttached ProcessThreadAttached 调用不是在worker thread 而是在 registers/deregister 这个module或者 start stop 这个module的时候 ** ** pacedsender是一个moudle -实现了...
Orange pi3初调试
因为树莓派沦为理财产品1年前出手殆尽后,现在唯一一个B性能不足一直没动力调试,沦为吃灰工具。 偶然之间多多给推了个orange产品预售,看了下pi3的参数,这不和赚了差价的3B一个性能吗?果断定了个预售款,在差…...

手机里的视频怎么转换成MP4格式?简单的转换方法分享
MP4格式是一种广泛使用的视频格式,几乎所有设备和操作系统都支持MP4格式的视频播放。无论是使用 iPhone、iPad、安卓手机、电视等各种设备,都可以播放 MP4 格式的视频。这种广泛的兼容性使得 MP4 成为一种非常方便的视频格式,我们可以随时随地…...
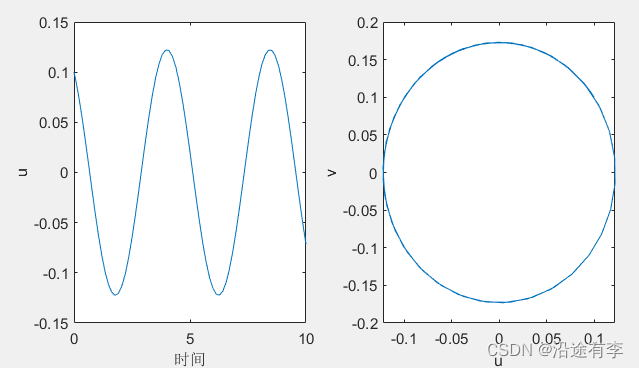
Matlab数学建模实战——(Lokta-Volterra掠食者-猎物方程)
1.题目 问题1 该数学建模的第一问和第二问主要是用Matlab求解微分方程组,直接编程即可。 求解 Step1改写 y(1)ry(2)f Step2得y的导数 y(1).2y(1)-ay(1)*y(2)y(2).-y(2)a*y(1)*y(2) Step3编程 clear; a0.01; F(t,y)[2*y(1)-a*y(1)*y(2);-y(2)a*y(1)*y(2)]; […...

windows下软件推荐
起源与目的 选择任何一个系统作为主力系统都是要好好考虑的。 在去年新买了一块1T的SSD后,就好好想了想这个问题。 Arch Linux, Ubuntu, Windows, macOS, deepin都是在考虑范围的。 不过我考虑到使用体验,最终还是选择了windows。 不选择macOS主要是不喜…...

SQlite数据库
SQlite数据库 1.SQLite简介 轻量化,易用的嵌入式数据库,用于设备端的数据管理,可以理解成单点的数据库。传统服务器型数据库用于管理多端设备,更加复杂 SQLite是一个无服务器的数据库,是自包含的。这也称为嵌入式数…...

Doris-问题
1.启动BE报错 设置系统最大打开文件句柄数(注意这里的*不要去掉) 重启生效!!!重启生效!!!重启生效!!! sudo vim /etc/security/limits.conf * soft nofile 65536 * hard nofile 65536 * soft nproc 131072 * hard nproc 131072 重启生效...

什么是OA系统,什么是工单系统,有啥区别?
一、OA系统与工单系统介绍 1、什么是OA系统 OA系统全称为Office Automation,即办公自动化系统。它是一种专门为企业和机构的日常办公工作提供服务的综合性软件平台,具有信息管理、流程管理、知识管理(档案和业务管理)、协同办公…...

DDoS攻击:网络安全的威胁
什么是DDoS攻击? DDoS(分布式拒绝服务)攻击是一种恶意网络攻击,目的是通过发送大量的请求或占用目标系统的资源,使其无法正常运行。在DDoS攻击中,攻击者使用分布在多个地理位置的多台计算机(也称…...

docker版jxTMS使用指南:device的调整
本文讲解4.2版jxTMS对device的调整,整个系列的文章请查看:docker版jxTMS使用指南:4.2版升级内容 docker版本的使用,请参考docker版jxTMS使用指南 4.0版jxTMS的说明,请查看:4.0版升级内容 为了适应拉取模…...

AI智能语音机器人的功能和作用都有哪些?
智能语音机器人是一种能够使用自然语言处理技术和人工智能算法,通过声音与用户进行交互的机器人。它可以回答用户提出的问题、处理用户的投诉、提供产品或服务的相关信息等等。 实现一个智能语音机器人需要涉及多个技术领域,包括自然语言处理、语音识别…...
vue3+vite+Ts 基于Antv/x6 绘制流程图
需求效果: 需求: 实现一个流程图,双击可对相应的组件进行一些功能操作; 工具栈: 这里使用antv/x6, 基于vue3vitets进行开发 官网地址: https://x6.antv.antgroup.com/examples/showcase/pra…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
