【数据挖掘】时间序列教程【九】
第5章 状态空间模型和卡尔曼滤波
状态空间模型通常试图描述具有两个特征的现象
-
有一个底层系统具有时变的动态关系,因此系统在时间上的“状态”t 与系统在时间的状态t−1有关 .如果我们知道系统在时间上的状态t−1 ,那么我们就有了我们需要知道的一切,以便对当时的状态进行推断或预测t .
-
我们无法观察到系统的真实底层状态,而是观察它的嘈杂版本。
这两个特征导致我们指定状态方程,它描述了系统如何从一个时间点演变到下一个时间点,以及观察方程,它描述了底层状态如何转换(添加噪声)为我们直接测量的东西。
假设有一个初始状态 .为t=1,2,... 我们希望能够估计后续状态
在每个时间点,我们都会观察到一些数据
我们希望将这些数据纳入我们的估计中
.
在最简单的情况下,我们可以提出一个观察方程
这里 和状态方程
这里 .参数θ τ 和σ 假设是已知的(您可以将它们视为调整参数),并且我们希望生成一个估计值
对于所有人t 感兴趣。回想一下,我们唯一观察到的是序列
状态空间模型可能最有意义的设置是动态设置,在该设置中,我们尝试估计状态值在“实时”中,不知道未来会发生什么。例如,在航天器的制导和导航应用中,我们想知道航天器在太空中行驶时的位置和速度,同时考虑到牛顿运动定律。根据我们对航天器位置和速度的估计,我们需要决定下一步该做什么。这种情况要求我们整合所有可用的信息,以产生最佳的估计。
5.1 示例:一个简单的航天器
假设我们乘坐宇宙飞船前往月球,我们刚刚点燃完引擎,让我们继续前进。当我们在太空中“航行”时,我们想知道我们离地球有多远,我们会定期看到恒星以估计我们的位置。
我们的“状态” 是我们的航天器与地球的径向距离。除非有任何加速度,如果航天器在时间
的位置是
,其速度是
,那么牛顿定律告诉我们它在时间 t 的位置是
是时间点之间经过的时间间隙,
表示一些噪声或轻微扰动(例如
。在某些情况下,我们可能会假设
。因此,这里的状态方程体现了“运动中的物体保持运动”的想法。
我们可以写这个方程,稍微不同,使用向量和矩阵作为
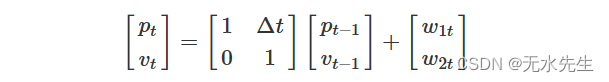
如果实际上没有加速度,我们知道速度不会随时间\(t-1\)到时间\(t\)而变化(也许除了一些轻微的扰动)。如果我们让
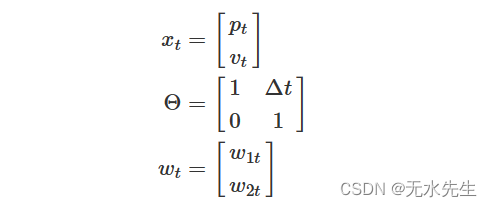
那么我们的状态方程就是
![]()
在这一点上,我们还没有讨论数据,但是如果没有对系统的任何观察,我们将不得不假设系统根据状态方程演变。因此,如果我们知道初始状态 ,我们对后续状态的最佳猜测将是
![]()
等等。这些与其说是“估计”(因为没有数据),不如说是基于我们对系统潜在动态的了解,对下一个状态应该是什么的预测。
那么问题是,如果我们在时间\观察数据
,我们应该怎么做?我们期望在时间 t 观察到什么?第二个问题可能是我们需要多久进行一次测量才能很好地估计我们的状态?
现在假设我们偶尔通过在航天器上进行的测量来观察我们的位置,并且在时间 我们观察到我们的位置
,即
所以 是我们真实位置的噪声测量(i.e
)。我们同样可以使用我们的状态向量将其完整形式编写为
如果我们让
然后我们有 ,我们的观察方程。一旦我们观察
\ ,我们对
的知识会如何变化?答案由卡尔曼滤波器给出。
5.2 卡尔曼滤波
有趣的事实:卡尔曼滤波器是由鲁道夫·卡尔曼在马里兰州巴尔的摩高等研究所工作时开发的。
为了介绍卡尔曼滤波器,让我们采用一个简单的模型,有时称为“局部水平”模型,其状态方程为
和观察方程
其中我们假设和
。基本的一维卡尔曼滤波算法如下。我们从初始状态
和初始方差
开始。从这里我们计算
作为我们对 和
的最佳猜测,给定我们当前状态。鉴于我们的新观察结果
,我们可以根据这个新信息更新我们的猜测,得到
这里:
对于一般情况,我们希望生成一个新的估计值 ,并且我们有当前状态
和方差
。
鉴于新的信息 ,然后我们可以更新我们的估计以获
这里:
是卡尔曼增益系数。 如果我们看一下卡尔曼增益的公式,很明显,如果测量噪声很高,那么 σ 2 很大,那么卡尔曼增益会更接近 0 ,以及新数据点的影响 y t 会很小。如果 σ 2 很小,那么过滤后的值 将会朝着以下方向进行更多调整
。在针对特定应用调整卡尔曼滤波算法时,记住这一点很重要。总体思路是

5.3 推导一维情况
有多种方法可以驱动卡尔曼滤波方程,但对于统计学家来说,最简单的方法可能是用正态分布来考虑一切。请记住,我们通常不会相信数据是按正态分布的,但我们可以将正态分布视为一种工作模型。我们将继续使用上面描述的局部模型
这里:和
让我们从 t = 1 我们将观察的地方 。假设我们有初始状态
。首先,我们想要得到边际分布
, IE。
。因为没有
我们还不能以任何观察到的信息为条件。我们可以计算
作为
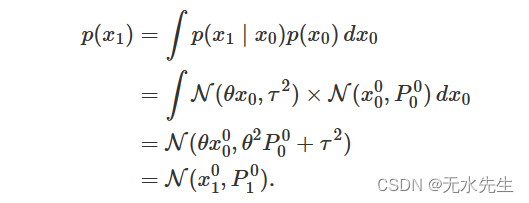
请注意,我们已经定义了 ;
。我们可以想到
这是我们根据我们对系统的了解而不是任何数据可以做出的最佳预测。 鉴于新的观察
我们想用这些信息来估计
。为此我们需要条件分布
,称为过滤密度。我们可以用贝叶斯法则来解决这个问题:
从观测方程我们知道 我们刚刚计算了
在上面。因此,利用正态分布的基本属性,我们有
这里:
是卡尔曼增益系数。那么对于 t = 1 我们有了新的估计
和
所以过滤密度为
现在让我们迭代一下这个过程 t = 2 我们现在将有一个新的观察结果 。我们想要计算新的过滤器密度
上面的陈述隐含的是 不依赖于
以价值为条件
。新的过滤密度
是观测数据历史的函数,是观测密度的乘积
和预测密度
。 在这种情况下,观测密度就是
。预测密度可以通过增加
与之前的状态值
在积分内部,我们有状态方程密度和滤波器密度的乘积 ,我们刚刚计算出
。状态方程密度为
过滤密度为
。将这些积分出来,我们得到
将我们刚刚计算的预测密度与观测密度相结合,我们得到
这里:
是新的卡尔曼增益系数。如果我们定义 和
那么我们就有了
。 我们怎么办
只是为了好玩?给出一个新的观察结果
,我们想要新的过滤器密度
使用与之前相同的想法,我们知道观察密度 预测密度为
现在新的过滤器密度是
此处:
总结一下,对于每个 t = 1 , 2 , 3 , …… 的估计 X t 是过滤密度的平均值 过滤密度是观测密度和预测密度的乘积,即
卡尔曼滤波算法的好处是我们递归地计算每个估计,因此不需要“保存”先前迭代的信息。每次迭代都内置了先前迭代的所有信息。
相关文章:
【数据挖掘】时间序列教程【九】
第5章 状态空间模型和卡尔曼滤波 状态空间模型通常试图描述具有两个特征的现象 有一个底层系统具有时变的动态关系,因此系统在时间上的“状态”t 与系统在时间的状态t−1有关 .如果我们知道系统在时间上的状态t−1 ,那么我们就有了我们需要知道的一切&am…...

数据结构---特殊矩阵和广义表
🌞欢迎来到机器学习的世界 🌈博客主页:卿云阁 💌欢迎关注🎉点赞👍收藏⭐️留言📝 🌟本文由卿云阁原创! 🙏作者水平很有限,如果发现错误ÿ…...

mysql数据库的定时备份脚本(docker环境和非docker环境)
一、非docker安装的MySQL MySQL作为一种常用的数据库管理系统,拥有着众多的优秀特性,如高性能、高可靠性、高可扩展性等。然而,在数据备份上,也需要我们进行一定的处理,这样才能保证数据的安全性。因此,在这里我们将介绍如何定时备份MySQL数据库。 我们可以通过MySQL自…...

【微信小程序】使用 wx.request 方法进行异步网络请求
在微信小程序中,你可以使用 wx.request 方法进行异步网络请求,并将获取到的列表数据渲染到 UI 上。 首先,在页面的 data 中定义一个数组变量,用于存储获取到的列表数据,例如: Page({data: {listData: [] …...
: You have an error in your SQL syntax;)
MySQL 8 修改root密码ERROR 1064 (42000): You have an error in your SQL syntax;
root先利用原密码登陆 mysql -u root -p Enter password: ******* Welcome to the MySQL monitor. Commands end with ; or \g. Your MySQL connection id is 9 Server version: 8.0.26 MySQL Community Server - GPLCopyright (c) 2000, 2021, Oracle and/or its affiliate…...
SpringCloud——分布式请求链路跟踪Sleuth
安装运行zipkin SpringCloud从F版已不需要自己构建Zipkin Server,只需要调用jar包即可 https://dl.bintray.com/oenzipkin/maven/io/zipkin/java/zipkin-server/ 下载:zipkin-server-2.12.9-exec.jar 运行:java -jar zipkin-server-2.12.9-e…...
【2 beego学习 - 项目导入与项目知识点】
0 项目导入 1 在英文路径下新建一个同名的项目,拷贝其他数据到这个文件 bee new 同名项目名 cd 同名项目名 go mod tidy go get -u -v github.com/astaxie/beego go get 同名项目名/models2 拷贝部分的项目文件到新目录 bee run 运行的其他错误,按照提示安装文件 1 后端获取…...
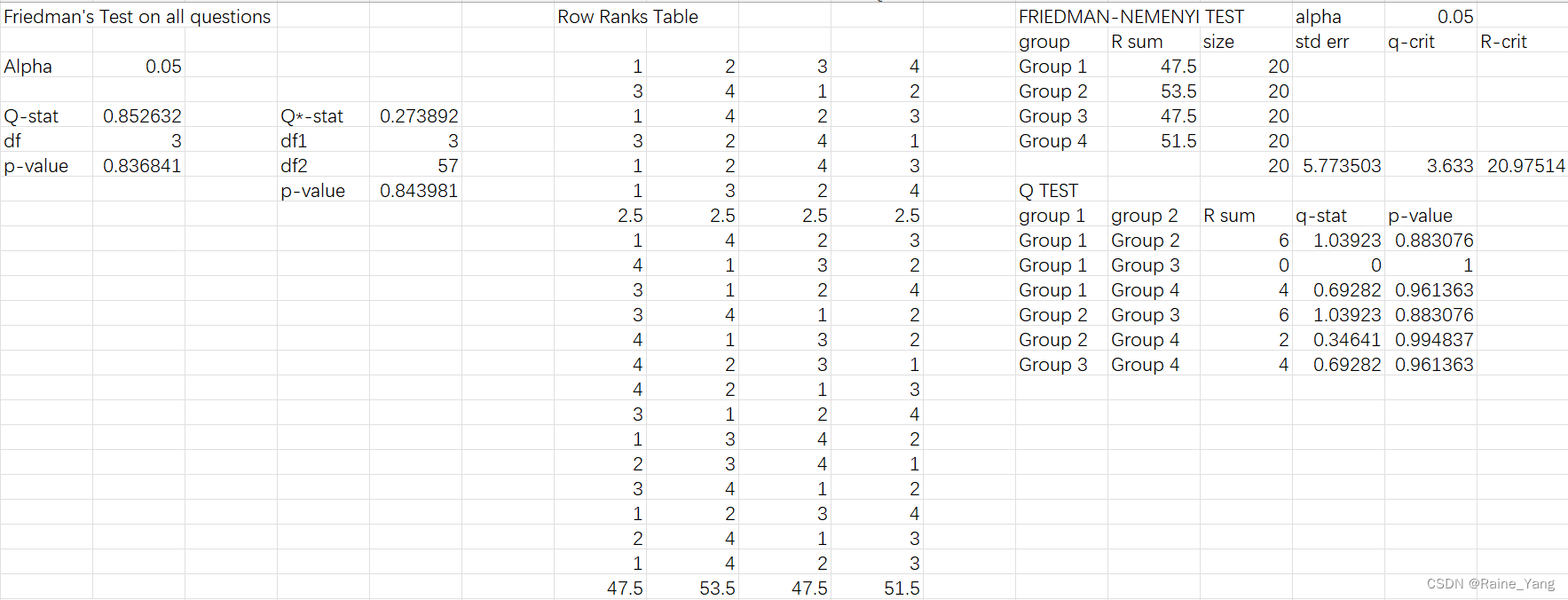
Langchain-ChatGLM配置文件参数测试
1 已知可能影响对话效果的参数(位于configs/model_config.py文件): # 文本分句长度 SENTENCE_SIZE 100# 匹配后单段上下文长度 CHUNK_SIZE 250 # 传入LLM的历史记录长度 LLM_HISTORY_LEN 3 # 知识库检索时返回的匹配内容条数 VECTO…...
和互斥锁(QReadWriteLock )的执行效率)
测试QT读写锁(QReadWriteLock )和互斥锁(QReadWriteLock )的执行效率
上代码: #include <QCoreApplication> #include <QElapsedTimer> #include <QtConcurrent> #include <QDebug>int main(int argc, char *argv[]) {QCoreApplication a(argc, argv);qSetMessagePattern("(%{time hh:mm:ss.zzz} %{thre…...
如何在 Windows 中免费合并 PDF 文件 [在线和离线]
PDF是一种广泛使用的文件格式,具有兼容性好、安全性高、易于打印、方便浏览等众多优点。在工作和学习过程中,经常需要将同一类型的PDF文件合并起来,以方便传输和查看,使得合并PDF文件成为一种重要的数据整合方法。 如果您想知道如…...
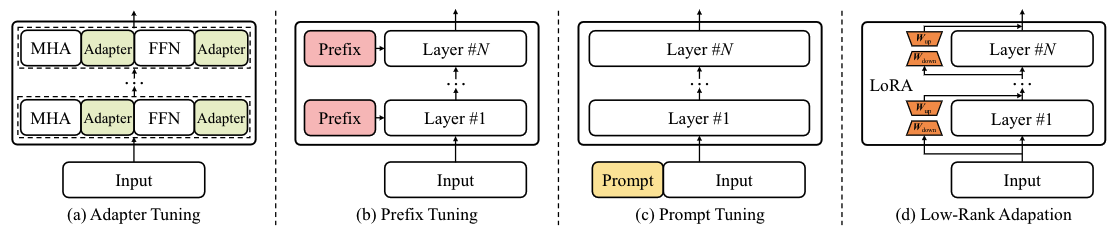
【LLM】金融大模型场景和大模型Lora微调实战
文章目录 一、金融大模型背景二、大模型的研究问题三、大模型技术路线四、LLaMA家族模型五、Lora模型微调的原理六、大模型Lora微调实战Reference 一、金融大模型背景 金融行业需要垂直领域LLM,因为存在金融安全和数据大多数存储在本地,在风控、精度、实…...
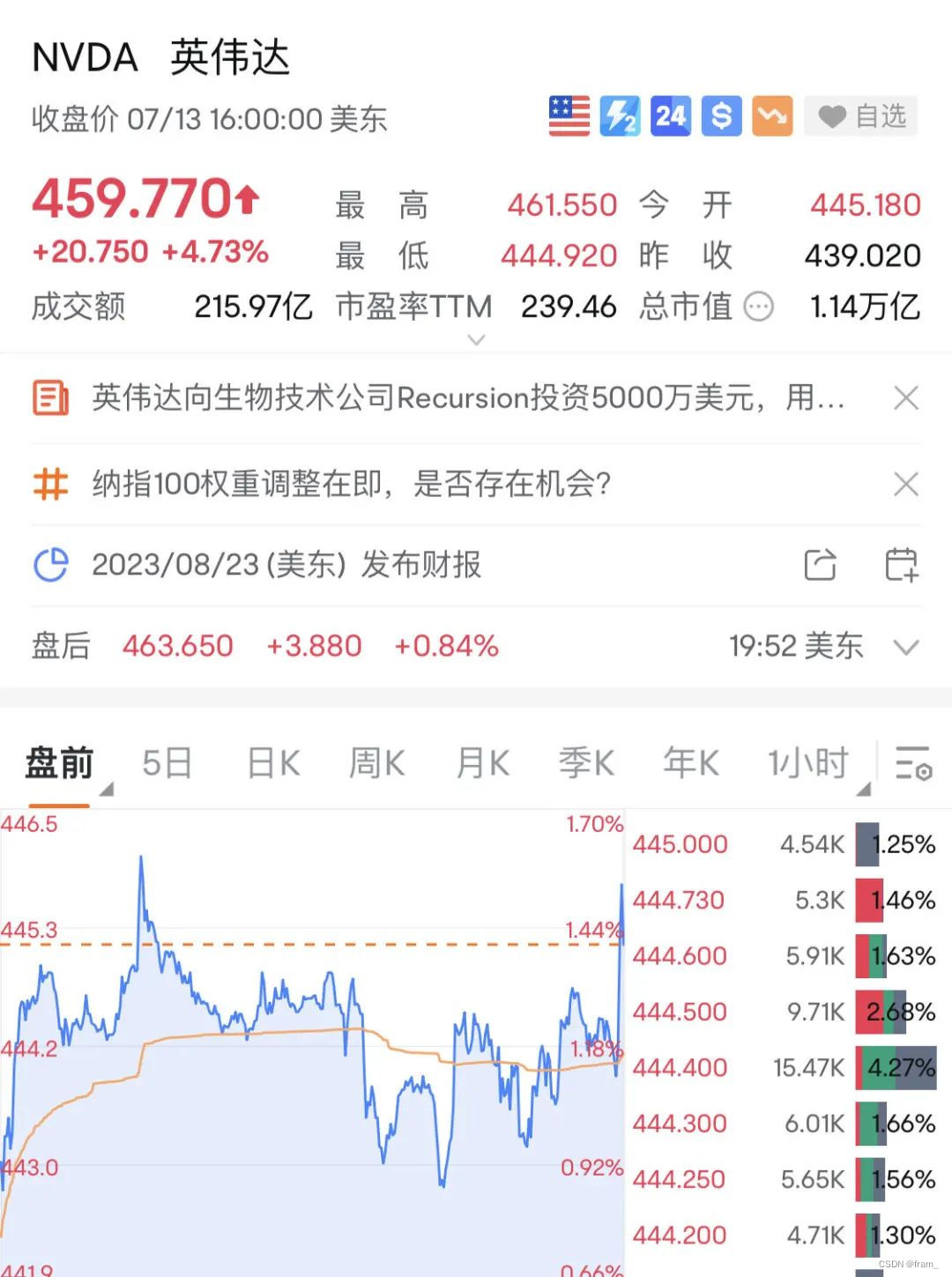
途乐证券股市资讯-英伟达,又创历史新高!美股全线上涨
当地时间13日,美股三大股指集体收涨,纳指、标普500指数双双改写2022年4月以来的新高。到收盘,道指涨0.14%,报34395.14点;纳指涨1.58%,报14138.57点;标普500指数涨0.85%,报4510.04点。…...

MySQL表聚合函数
前言 哈喽,各位小伙伴大家好,本篇文章为大家介绍几个MySQL中常用的聚合函数,什么是聚合函数,相信第一次看到这个名词的小伙伴是比较懵的,举个例子,比如说统计表中数据的个数,就可以使用MySQL中提…...
JavaWeb 速通XML
目录 一、XML快速入门 1.基本介绍 : 2.入门案例 : 二、XML语法 0.文件结构 : 1.文档声明 : 2. 元素 : 3.属性 : 4.注释 : 5.CDATA节 : PS : XML转义符 : 三、Dom4j 1.关于XML解析技术 : 2 Dom4j介绍 : 3.Dom4j使用 : 1 获取Document对象的三种方式 2 …...
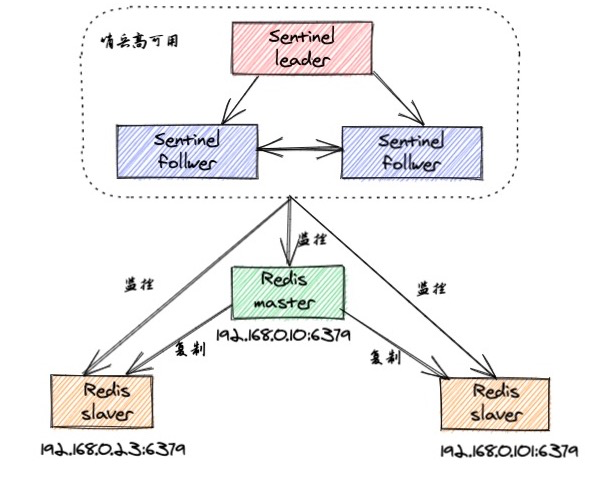
redis浅析
一 什么是NoSQL? Nosql not only sql(不仅仅是SQL) 关系型数据库:列行,同一个表下数据的结构是一样的。 非关系型数据库:数据存储没有固定的格式,并且可以进行横向扩展。 NoSQL泛指非关系…...

四种缓存的避坑总结
背景 分布式、缓存、异步和多线程被称为互联网开发的四大法宝。今天我总结一下项目开发中常接触的四种缓存实际项目中遇到过的问题。 JVM堆内缓存 JVM堆内缓存因为可以避免memcache、redis等集中式缓存网络通信故障问题,目前还在项目中广泛使用。 堆内缓存需要注…...

flutter开发实战-flutter二维码条形码扫一扫功能实现
flutter开发实战-flutter二维码条形码扫一扫功能实现 flutter开发实战-flutter二维码扫一扫功能实现,要使用到摄像头的原生的功能,使用的是插件:scan 效果图如下 一、扫一扫插件scan # 扫一扫scan: ^1.6.01.1 iOS权限设置 <key>NSCa…...

一篇文章了解Redis分布式锁
Redis分布式锁 什么是分布式锁? redis分布式锁是一种基于redis实现的锁机制,它用于在多并发分布式环境下控制并发访问共享资源。在多个应用程序或是进程访问共享资源时,分布式锁可以确保只有一个进程可以访问该资源,不会发生…...

记录第一次组装电脑遇到的坑
京东装机大师配置清单如下: 主板cpu安装 本次安装拆了两次主板 原因1.主板侧面有个金属板需要从内部安装 2.cpu风扇有个板需要装在主板底下 显卡比较大个要最后装,要不然可能要拆好几次 装系统时候 u盘启动认不出来,他妈的是因为机箱上的usb…...
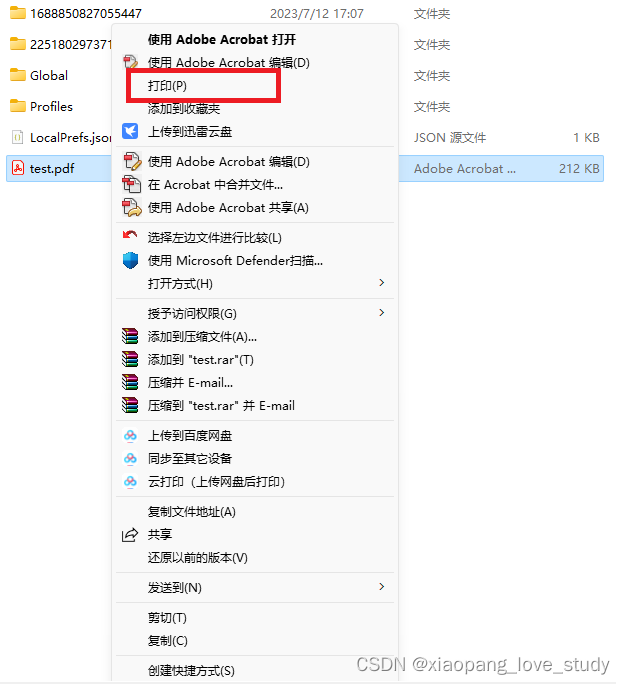
右键pdf文件没有打印
问题描述 右键点pdf文件,弹出的菜单找不到打印选项。网上找了很多办法,然并卵啊。还是得靠自己慢慢摸索。 原因分析 新安装的win11系统,pdf文件默认可以用windows自带的edge浏览器打开。但是edge浏览器没有能力提供右键打印功能。 解决办法…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
