最大连续子列和
给定一个数组,求它的最大连续子列和。
这个问题有四种解法。
1、暴力循环(O(n^3))
分析这个问题,既然是子列,那么它最长为n,最短为1。要想求和我们一般需要知道这个子列的左端下标和右端下标,再求这个子列的和。最简单的办法就是用暴力循环来求和。
首先我们需要定义左端下标i,每次循环i++。接下来是右端下标j,j的初值为i,因为右端下标总是大于等于左端下标,每次循环j++。知道了左端下标i和右端下标j之后,再从i到j循环求和就行了。
#include <iostream>
#include <algorithm>using namespace std;const int N=1*10^6;int main()
{int n;cin>>n;int a[N];int sum=0,maxsum=0;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++){for(int j=i;j<n;j++){sum=0;for(int k=i;k<=j;k++) sum+=a[k];if(sum>maxsum) maxsum=sum;}}cout<<maxsum;return 0;
} 2、暴力循环的改进(O(n^2))
第一种算法显然时间复杂度太高了,可以进行改进,减少一层循环。
当左端下标i和右端下标j确定时,知道a[i]~a[j]的和,如果要求a[i]~a[j+1],按照第一种算法,需要重新遍历一遍a[i]~a[j]的数组,再把a[j+1]加上。思考后,我们发现,如果已知a[i]~a[j]的和sum,我们只需要让sum+a[j+1]就可以得到a[i]~a[[j+1]的和。因此我们就可以使用两层循环就可以解决这个问题。
#include <iostream>
#include <algorithm>using namespace std;const int N=1*10^6;int main()
{int n;cin>>n;int a[N];int sum=0,maxsum=0;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++){sum=0;for(int j=i;j<n;j++){sum+=a[j];if(sum>maxsum) maxsum=sum;}}cout<<maxsum;return 0;
}值得注意的是,第一个算法中sum重置为0是在第二个循环里,第二个sum重置为0是在第一层循环里。原因是第一个算法的第三层循环是循环累加求值,所以每次循环前要重置为0,而第二个算法简化后,左端i确定后,利用累加的方法记录以左端i为首长度为1~n-i+1的各子列的和,所以在第一重循环确定新的左端i后,就要重置sum。
3、分治(O(n*logn))
当我们看到一个算法的时间复杂度是O(n^2)的时候,我们就可以思考这个算法能不能经过改进将时间复杂度降为O(n*logn)
这个问题也可以用分治的方法来解决。(有时候想想这些算法题真操蛋,万物可分治可二分可递归了^_^)
分治是将大的问题划分成小的问题,最后整合结果的方法。分是划分,治是整合结果。
怎么分治呢?我们考虑到,把整个数列从中间切开,最大子列和=max(左边数列最大子列和,右边数列子列和,跨越边界的子列和),跨越边界的子列和就是左右两边的数都包含的情况。利用这个办法,不断地将子列切片,进行分治,最终就能求得整个数列的最大子列和。
代码有点复杂,回头有空再写吧^_^4、在线处理!(O(n))!
这是对于最大子列和最好最快的算法。
这个算法的思想是,从左到右累加每个数得到sum,如果sum>maxsum,更新maxsum=sum,如果sum<0,将sum重置为0。输出最后的sum值。
为什么这个算法是正确的呢?如果任意一个子列和小于0,那么这个子列一定不会位于和最大子列的左侧,因为一个负数对于整个数列的和是没有贡献的。
#include <iostream>
#include <algorithm>using namespace std;const int N=1*10^6;int main()
{int n;cin>>n;int a[N];int sum=0,maxsum=-1*10^6;for(int i=0;i<n;i++){cin>>a[i];sum+=a[i];if(sum<0) sum=0;if(sum>maxsum) maxsum=sum;}cout<<maxsum;return 0;
}为什么,我把maxsum设为负数呢,因为有的算法题给的数据实在变态,你必须考虑符合题意的每一种极端情况。把maxusm设置为负数,我是考虑到,只有一个元素且为负数的情况。
为什么它叫在线处理呢?因为它可以边输入边计算,只需要一个循环。而算法复杂度只能这么小了,毕竟输入数据的算法也需要O(n)。
这四种算法思想均来自中国大学mooc陈越老师的数据结构课。
md,真爽,还有啥比ac更爽的?!纠结这么久终于找到bug,解决这道题了。
相关文章:

最大连续子列和
给定一个数组,求它的最大连续子列和。这个问题有四种解法。 1、暴力循环(O(n^3))分析这个问题,既然是子列,那么它最长为n,最短为1。要想求和我们一般需要知道这个子列的左端下标和右端下标,再求这个子列的和。最简单的…...
线性基 学习笔记
什么是线性基? 先来回顾一下向量空间中的基。这个基代表着空间的一个极大线性无关子集,组中向量线性无关,且空间中的任意一个向量都可以唯一地由基中的向量来表示 那么回到线性基,它其实就类似于是一个向量空间的基 我们考虑一…...

算法-回溯算法-组合问题
77. 组合https://leetcode.cn/problems/combinations/ 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,…...

ABAP中的Null值与space 以及 BW中ADSO的Key值
写出来怪丢人,到现在还没搞懂这个。 在BW中创建ADSO,定义Key字段。可以看到ADSO表的定义中,所有的Key和Data属性如下: 所有的key会有关键字key打头,所有字段都有not null. 但是并不是有个字段是blank空的就不能更新进…...

JavaScript库之Lodash常用方法
Lodash 中文文档https://www.lodashjs.com/docs/lodash.omit/以下总结了在项目中常用的方法,其他的慢慢更新语言:cloneDeep这个方法类似_.clone,除了它会递归拷贝 value。(注:也叫深拷贝)参数value (*): 要…...
Kotlin新手教程二(Kotlin基本数据类型及基础语法)
一、基本数据类型 1.数字 由于Kotlin支持类型推断,所以在使用时若超出Int的范围则会被认定为其它类型;若需要显式指定Long型值,则需要在值后添加L后缀。 2.浮点数 3.比较两个数( 和 ) Kotlin 中没有基础数据类型&a…...
git idea创建新分支,获取/合并主支代码的2个方法
其他sql格式也在更新中,可直接查看这个系列,要是没有你需要的格式,可在评论或私信我 个人目录 获取主支代码的2个方法1,创建一个分支,获取主支的所有代码(场景:我需要一个自己的分支进行编写模…...

CF1714A Everyone Loves to Sleep 题解
CF1714A Everyone Loves to Sleep 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例解释题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1代码实现题目 链接 https://www.luogu.com.cn/problem/CF1714A 字面描述 题面翻译 题目描述 Vlad和其他人一样&am…...
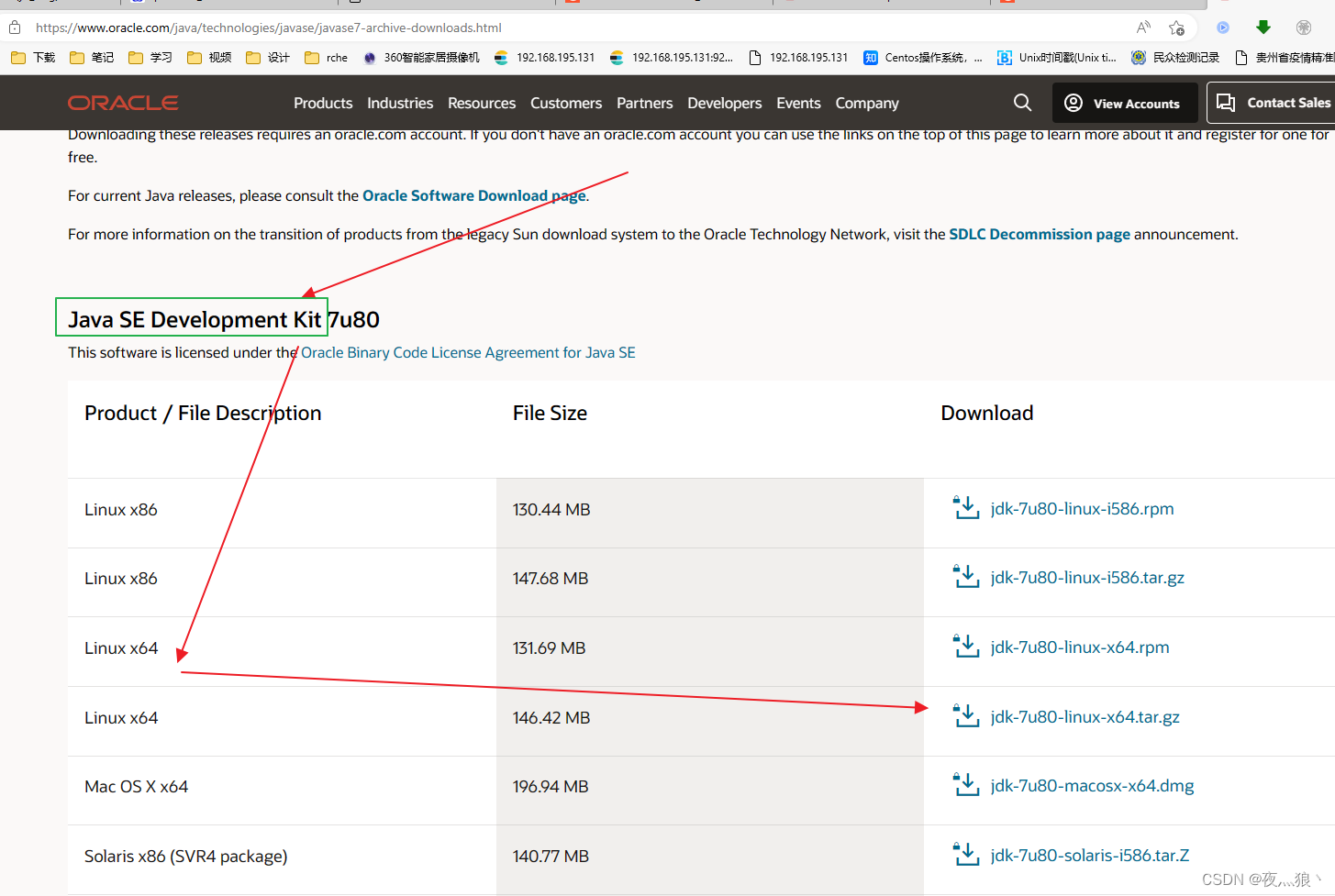
oracle官方下载历史版本JDK版本
背景 日常工作中由于一些特殊原因,我们需要下载指定系统指定位数指定版本的jdk,这个时候去网上搜索下载就会遇到各种坑,病毒、诱导连接、诱导关注/注册、付费、错误版本等,所以最好的办法是去官网下载,下面列举两种方式…...

双击-jar包无法运行解决方法
我自己是通过探索出来的方法解决的,网上的方法适合普通问题 网络流传方法 那种-jar和run.bat的就是曲解了问题意思,问题不是如何运行,而是如何双击jar包就可以直接运行。 普通小问题就是修改注册表,将java路径写进去后面加个 %1…...
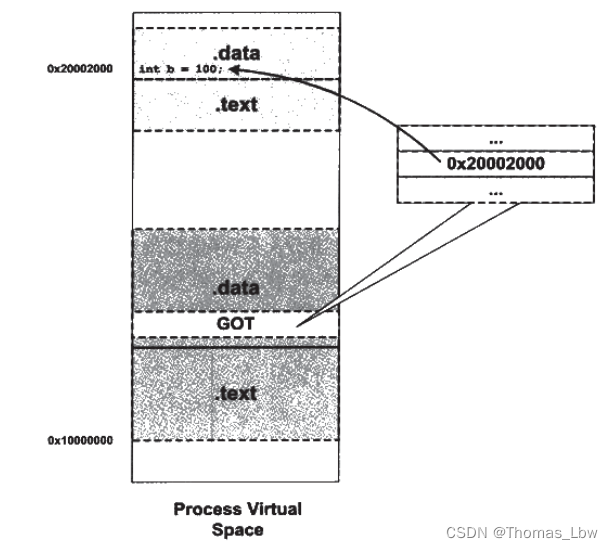
程序员的自我修养第七章——动态链接 (下)
接上一篇。 7.3 地址无关代码 对于现代机器来说,引入地址无关代码并不麻烦,我们展示下各种模型的地址引用方式: 1. 模块内部函数调用 2. 模块内部的数据访问,如全局变量、静态变量。 3. 模块外部的函数调用,跳转。 4.…...
蓝桥杯刷题——基础篇(二)
这部分题目,主要面向有志参加ACM与蓝桥杯竞赛的同学而准备的,蓝桥杯与ACM考察内容甚至评测标准基本都一样,因此本训练计划提供完整的刷题顺序,循序渐进,提高代码量,巩固基础。因竞赛支持C语言、C、Java甚至…...
)
PTA L1-049 天梯赛座位分配(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: 天梯赛每年有大量参赛队员,要保证同一所学校的所有队员都不能相邻,分配座位就成为一件比较麻烦的事情。为此我们制定如下策…...

Linux部分参数作用讲解
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

Java kafka
JAVA面试题--Kafka(最新最全) 目录概述需求:设计思路实现思路分析1.URL管理2.网页下载器3.爬虫调度器4.网页解析器5.数据处理器拓展实现性能参数测试:参考资料和推荐阅读)Survive by day and develop by night. talk for import b…...

DBA之路---Stream数据共享同步机制与配置方法
oracle的Stream解析–数据共享 在g版本常用,如果是c版本项目一般都会选择goldengate,比stream靠谱多了 Oracle中的stream是消息队列一种应用形式,原理如下: 收集oracle中的事件,将事件保存在队列里,然后将…...

CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1790E 字面描述 题面翻译 共有 ttt 组数据。 每组数据你会得到一个正整数 xxx&…...

漏洞预警|Apache Kafka Connect JNDI注入漏洞
棱镜七彩安全预警 近日网上有关于开源项目Apache Kafka Connect JNDI注入漏洞,棱镜七彩威胁情报团队第一时间探测到,经分析研判,向全社会发起开源漏洞预警公告,提醒相关安全团队及时响应。 项目介绍 Karaf是Apache旗下的一个开…...

企业小程序开发步骤【教你创建小程序】
随着移动互联网的兴起,微信已经成为了很多企业和商家必备的平台,而其中,微信小程序是一个非常重要的工具。本文将为大家介绍小程序开发步骤,教你创建小程序。 步骤一、注册小程序账号 先准备一个小程序账号,在微信公…...

刚性电路板的特点及与柔性电路板的区别
打开市场上的任何一个电子产品,会发现里面都有一块或多块电路板。电路板是电子产品运行的核心,之前沐渥小编已经给大家介绍了柔性电路板,下面给大家介绍刚性电路板的基础知识。 刚性电路板俗称硬板,是由不容易变形的刚性基材制成的…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
