【Python机器学习】实验01 Numpy以及可视化回顾
文章目录
- 一、Numpy的基础知识
- 实验1 生成由随机数组成的三通道图片,分别显示每个维度图片,并将三个通道的像素四周进行填充,分别从上下左右各填充若干数据。
- 二、Numpy的线性代数运算
- 实验2 请准备一张图片,按照上面的过程进行矩阵奇异分解,要求保存前50个特征值进行压缩。
一、Numpy的基础知识
- 创建列表
import numpy as np
np.array([1,2,3])
array([1, 2, 3])
np.array([[1,2],[2,3]])
array([[1, 2],[2, 3]])
- 快捷方式创建列表
np.arange(1,10),np.arange(10,1,-1)
(array([1, 2, 3, 4, 5, 6, 7, 8, 9]),array([10, 9, 8, 7, 6, 5, 4, 3, 2]))
range(10,1,-1)
range(10, 1, -1)
np.linspace(1,10,5)
array([ 1. , 3.25, 5.5 , 7.75, 10. ])
np.zeros((2,2))
array([[0., 0.],[0., 0.]])
np.ones((1,1))
array([[1.]])
np.diag([1,2])
array([[1, 0],[0, 2]])
- 采用随机数生成数组
import numpy.random as rd
rd.uniform(2,3,[3,4])
array([[2.00870568, 2.84081335, 2.56773483, 2.31232497],[2.4091653 , 2.22513678, 2.62473312, 2.20786884],[2.8608431 , 2.04426497, 2.73712184, 2.73669482]])
rd.random((1,3))
array([[0.33035627, 0.1179577 , 0.68061576]])
rd.normal(2,6,(2,4))
array([[ 5.6250594 , 8.07709039, 1.92724817, -4.75702484],[-1.71722434, 2.69880337, -6.20162398, -0.62033363]])
- 利用随机数生成图片
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt
plt.figure(figsize=(2,2))
img=rd.randint(0,255,(10,10))
plt.imshow(img)
<matplotlib.image.AxesImage at 0x243604a2250>
arr1=rd.randn(1,3)
arr1.astype("float32")
array([[ 0.47883075, -0.5455359 , -1.2719026 ]], dtype=float32)
- 数组常见属性
arr1.shape,arr1.T,arr1.dtype,arr1.ndim
((1, 3),array([[ 0.47883076],[-0.54553593],[-1.27190261]]),dtype('float64'),2)
- 数组的访问
arr=np.arange(1,10).reshape(3,3)
arr
array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
plt.figure(figsize=(2,2))
plt.imshow(arr)
<matplotlib.image.AxesImage at 0x24360c1ed00>
arr[:2,:2]
array([[1, 2],[4, 5]])
arr[[0,2],:2]
array([[1, 2],[7, 8]])
arr.T
plt.figure(figsize=(2,2))
plt.imshow(arr.T)
<matplotlib.image.AxesImage at 0x24360c78af0>

arr[::-1,]
plt.figure(figsize=(2,2))
plt.imshow(arr[::-1,])
<matplotlib.image.AxesImage at 0x24360ccdd30>
arr[::-1,].T
plt.figure(figsize=(2,2))
plt.imshow(arr[::-1,].T)
<matplotlib.image.AxesImage at 0x24360d24e20>
arr.T[::-1,]
plt.figure(figsize=(2,2))
plt.imshow(arr.T[::-1,])
<matplotlib.image.AxesImage at 0x24360d78a30>

arr.T[::,::-1]
plt.figure(figsize=(2,2))
plt.imshow(arr.T[::,::-1])
<matplotlib.image.AxesImage at 0x24360dcc730>
- 可视化2*2像素的一张图
import matplotlib.pyplot as plt
plt.figure(figsize=(2,2))
plt.imshow([[0,1],[1,0]])
<matplotlib.image.AxesImage at 0x24360e24340>
- 数组的应用np.insert,np.concatenate,np.stack,np.tile
from scipy import misc
plt.figure(figsize=(2,2))
img = misc.face()
plt.imshow(img)
<matplotlib.image.AxesImage at 0x24360ef4be0>

img.shape
(768, 1024, 3)
plt.figure(figsize=(2,2))
plt.imshow(img[:,:512,:])
<matplotlib.image.AxesImage at 0x24361197ca0>

plt.figure(figsize=(2,2))
plt.imshow(img[:384,:,:])
<matplotlib.image.AxesImage at 0x2436131cd00>

plt.figure(figsize=(2,2))
plt.imshow(img[:,:,2])
<matplotlib.image.AxesImage at 0x2436149bcd0>

img_r=img[:,:,2]
plt.figure(figsize=(2,2))
plt.imshow(img_r[::-1,:])
<matplotlib.image.AxesImage at 0x243614f7250>

img_r=img[:,:,2]
plt.figure(figsize=(2,2))
plt.imshow(img_r[::,::-1])
<matplotlib.image.AxesImage at 0x2436154b4c0>

img_new=np.insert(img_r,0,img_r[:50],axis=0)
plt.figure(figsize=(2,2))
plt.imshow(img_new)
<matplotlib.image.AxesImage at 0x2436159b790>

img_new=np.insert(img_r,0,img_r[:,:100].T,axis=1)
plt.figure(figsize=(2,2))
plt.imshow(img_new)
<matplotlib.image.AxesImage at 0x243615f0f40>
plt.figure(figsize=(2,2))
plt.imshow(np.concatenate([img_r,img_r],axis=1))
<matplotlib.image.AxesImage at 0x24362a74c10>

plt.figure(figsize=(2,2))
plt.imshow(np.concatenate([img_r,img_r],axis=0))
<matplotlib.image.AxesImage at 0x243628f9be0>

plt.figure(figsize=(2,2))
plt.imshow(np.stack([img_r,img_r],axis=0)[0])
<matplotlib.image.AxesImage at 0x2436294cdf0>

实验1 生成由随机数组成的三通道图片,分别显示每个维度图片,并将三个通道的像素四周进行填充,分别从上下左右各填充若干数据。
程序设计
#利用随机数生成图片
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(4,4))#四张子图
ax1=fig.add_subplot(221)
ax2=fig.add_subplot(222)
ax3=fig.add_subplot(223)
ax4=fig.add_subplot(224)#用随机数数组填充子图
img=rd.randint(0,255,(10,10))
ax1.imshow(img)
ax2.imshow(img)
ax3.imshow(img)
ax4.imshow(img) #从上方填充
img1=np.insert(img,0,img[0,:],axis=0)
ax1.imshow(img1)#从下面填充
img2=np.insert(img,-1,img[-1,:],axis=0)
ax2.imshow(img2)#从左边填充
img3=np.insert(img,0,img[:,0],axis=1)
ax3.imshow(img3)#从右边填充
img4=np.insert(img,-1,img[:,-1],axis=1)
ax4.imshow(img4)plt.tight_layout()
plt.show()
具体分析
这段代码是利用随机数生成图片,并在将图片填充到四个子图中展示。以下是代码的具体分析:
- 导入numpy库,用于生成随机数和操作数组;导入matplotlib库,用于绘制图像。
- 创建一个大小为4x4的Figure对象,即一个包含4个子图的画布。
- 使用add_subplot()函数创建四个子图对象ax1、ax2、ax3和ax4。
- 使用randint()函数生成一个10x10的随机数数组img,并将其作为参数传递给imshow()函数并分别绘制到四个子图上。
- 从上方填充子图1(ax1):使用insert()函数在数组img的第一行之前插入第一行,并将结果赋给img1。然后使用imshow()函数在子图1上展示img1。
- 从下方填充子图2(ax2):使用insert()函数在数组img的倒数第一行之前插入最后一行,并将结果赋给img2。然后使用imshow()函数在子图2上展示img2。
- 从左边填充子图3(ax3):使用insert()函数在数组img的第一列之前插入第一列,并将结果赋给img3。然后使用imshow()函数在子图3上展示img3。
- 从右边填充子图4(ax4):使用insert()函数在数组img的倒数第一列之前插入最后一列,并将结果赋给img4。然后使用imshow()函数在子图4上展示img4。
- 使用tight_layout()函数调整子图的布局,使其适应画布。
- 使用show()函数显示画布和子图。
二、Numpy的线性代数运算
import numpy.linalg as la
arr1=np.arange(1,5).reshape(2,2)
arr1
array([[1, 2],[3, 4]])
la.det(arr1)
-2.0000000000000004
la.inv(arr1)
array([[-2. , 1. ],[ 1.5, -0.5]])
arr1@la.inv(arr1)
array([[1.00000000e+00, 1.11022302e-16],[0.00000000e+00, 1.00000000e+00]])
np.dot(arr1,la.inv(arr1))
array([[1.00000000e+00, 1.11022302e-16],[0.00000000e+00, 1.00000000e+00]])
#矩阵奇异分解
U,s,V=la.svd(arr1)
U,s,V
(array([[-0.40455358, -0.9145143 ],[-0.9145143 , 0.40455358]]),array([5.4649857 , 0.36596619]),array([[-0.57604844, -0.81741556],[ 0.81741556, -0.57604844]]))
注意, s是个对角方阵,这里用一维数组做了简写。
np.diag(s) 是其本该有的样子。
#重构矩阵
U@np.diag(s)@V
array([[1., 2.],[3., 4.]])
plt.figure(figsize=(2,2))
plt.imshow(img_r,cmap="hot")
<matplotlib.image.AxesImage at 0x24362cde2b0>

U,s,V=la.svd(img_r)
U.shape,s.shape,V.shape
((768, 768), (768,), (1024, 1024))
#重构图像
S=np.zeros((U.shape[1],V.shape[0]))
np.fill_diagonal(S,s)
S.shape
(768, 1024)
plt.imshow(U@S@V)
<matplotlib.image.AxesImage at 0x24362d45160>

#只用一部分来重构图像
k=500
appro_imag=U@S[:,:20]@V[:20,:]
plt.imshow(appro_imag)
<matplotlib.image.AxesImage at 0x2436554cdc0>

结论: 使用奇异值分解可以获得图像的近似表示。此技术可以用于图像压缩或者,图像的主成分分析。
appro_imag.shape
(768, 1024)
实验2 请准备一张图片,按照上面的过程进行矩阵奇异分解,要求保存前50个特征值进行压缩。
程序设计
from PIL import Image
image = misc.ascent()
plt.imshow(image)
<matplotlib.image.AxesImage at 0x243661b3340>

U,s,V=la.svd(image)
U.shape,s.shape,V.shape
S=np.zeros((U.shape[1],V.shape[0]))
np.fill_diagonal(S,s)
k=50
appro_imag=U@S[:,:k]@V[:k,:]
plt.imshow(appro_imag)
<matplotlib.image.AxesImage at 0x2436348dc10>

具体分析
这段代码使用了PIL库中的Image模块,通过其ascent()函数生成了一个图像。然后使用numpy和scipy的线性代数函数对图像进行奇异值分解(SVD)处理。以下是代码的具体分析:
- 导入PIL库中的Image模块。
- 使用ascent()函数生成一个图像image。
- 使用numpy的线性代数函数la.svd()对图像进行奇异值分解,将结果分别赋给U、s和V三个变量。
- 使用U.shape、s.shape和V.shape分别获得U、s和V的形状(维度)信息,并输出。
- 创建一个全零矩阵S,其行数为U的列数,列数为V的行数。
- 使用numpy的fill_diagonal()函数将s数组中的元素按对角线方向填充到S矩阵之中,通过对角线填充的方式将奇异值转化为奇异值矩阵。
- 设置一个参数k为50,表示提取前k个奇异值和对应的奇异向量。
- 使用U、S和V的切片操作,分别选取前k列的奇异向量和前k行的奇异值矩阵,并通过矩阵乘法运算得到近似图像。
- 使用plt的imshow()函数将近似图像显示出来。
总体而言,这段代码是对图像进行奇异值分解,并根据提取到的奇异值和奇异向量重构了一个近似图像,并将其显示出来。
相关文章:

【Python机器学习】实验01 Numpy以及可视化回顾
文章目录 一、Numpy的基础知识实验1 生成由随机数组成的三通道图片,分别显示每个维度图片,并将三个通道的像素四周进行填充,分别从上下左右各填充若干数据。 二、Numpy的线性代数运算实验2 请准备一张图片,按照上面的过程进行矩阵…...
vue3-组件中的变化
1. 路由 1. 安装指令:npm i vue-routernext 2. 创建路由:createRouter2. 异步组件(defineAsyncComponent) defineAsyncComponent 是用于定义异步组件的函数。defineAsyncComponent 接受一个工厂函数作为参数,这个工厂…...
认识主被动无人机遥感数据、预处理无人机遥感数据、定量估算农林植被关键性状、期刊论文插图精细制作与Appdesigner应用开发
目录 第一章、认识主被动无人机遥感数据 第二章、预处理无人机遥感数据 第三章、定量估算农林植被关键性状 第四章、期刊论文插图精细制作与Appdesigner应用开发 更多推荐 遥感技术作为一种空间大数据手段,能够从多时、多维、多地等角度,获取大量的…...

数学建模的六个步骤
一、模型准备 了解问题的实际背景,明确其实际意义,掌握对象的各种信息,以数学思路来解释问题的精髓,数学思路贯彻问题的全过程,进而用数学语言来描述问题。要求符合数学理论,符合数学习惯,清晰…...
【计算机组成原理】24王道考研笔记——第二章 数据的表示和运算
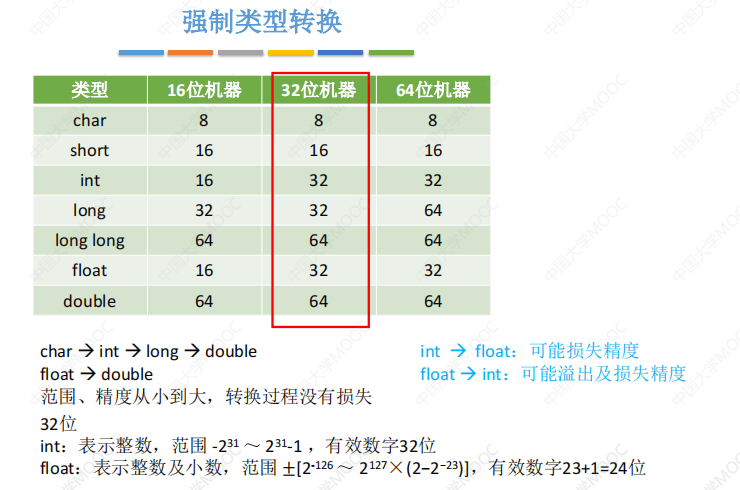
第二章 数据的表示和运算 一、数值与编码 1.1 进制转换 任意进制->十进制: 二进制<->八进制、十六进制: 各种进制的常见书写方式: 十进制->任意进制:(用拼凑法最快) 真值:符合人…...

JQ-6 Bootstrap入门到实战;Bootstrap的(优缺点、安装、响应式容器原理、网格系统、响应式工具类、Bootstrap组件);小项目实践
目录 1_认识Bootstrap1.1_概念1.2_起源和历史1.3_Bootstrap优缺点 2_Bootstrap4的安装2.1_方式一 CDN2.2_方式二 : 下载源码引入2.3_方式三 : npm安装 3_Bootstrap初体验4_响应式容器原理4.1_屏幕尺寸的分割点(Breakpoints)4.2_响应式容器Containers 5_网…...
如何用3D格式转换工具HOOPS Exchange读取颜色和材料信息?
作为应用程序开发人员,非常希望导入部件的图形表示与它们在创作软件中的外观尽可能接近。外观可以在每个B-Rep面的基础上指定,而且,通过装配层次结构的特定路径可以在视觉外观上赋予父/子覆盖。HOOPS ExchangeHOOPS Exchange可捕获有关来自各…...

[Ubuntu 22.04] 安装docker,并设置镜像加速
for pkg in docker.io docker-doc docker-compose podman-docker containerd runc; do sudo apt-get remove $pkg; doneapt install -y curl vim wget gnupg dpkg apt-transport-https lsb-release ca-certificates# 添加Docker的GPG公钥和apt源 #curl -sSL https://download.d…...
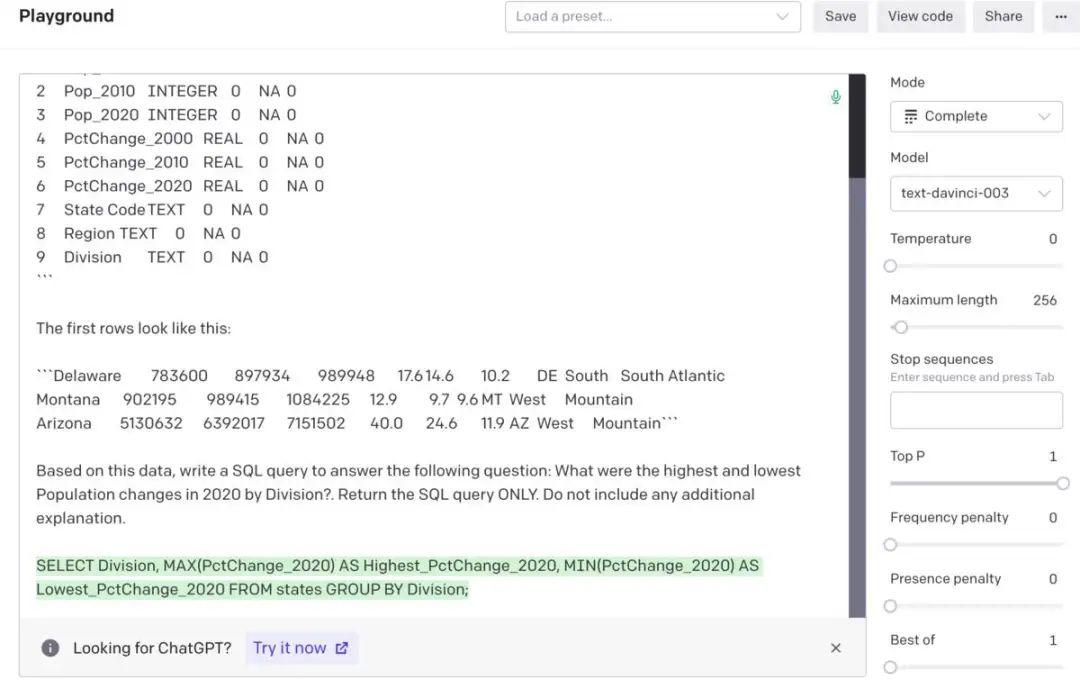
如何使用GPT作为SQL查询引擎的自然语言
生成的AI输出并不总是可靠的,但是下面我会讲述如何改进你的代码和查询的方法,以及防止发送敏感数据的方法。与大多数生成式AI一样,OpenAI的API的结果仍然不完美,这意味着我们不能完全信任它们。幸运的是,现在我们可以…...

Servlet3.0上传文件
页面: <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>文件上传</title> </head> <body> <form action"fileup" enctype"multipart/form-data" method"…...

【ARM Cache 系列文章 6 番外篇 – MMU, MPU, SMMU, PMU 差异与关系】
文章目录 MMU 与 MPU 之间的关系MMU 与 SMMU 之间的关系MMU 与 PMU 之间的关系 上篇文章:ARM Cache 系列文章 5 – 内存屏障ISB/DSB/DMB MMU 与 MPU 之间的关系 MMU(Memory Management Unit)和MPU(Memory Protection Unit&#…...

NetSuite ERP顾问的进阶之路
目录 1.修养篇 1.1“道”是什么?“器”是什么? 1.2 读书这件事儿 1.3 十年计划的力量 1.3.1 一日三省 1.3.2 顾问损益表 1.3.3 阶段课题 2.行为篇 2.1协作 2.2交流 2.3文档管理 2.4时间管理 3.成长篇 3.1概念能力 3.1.1顾问的知识结构 …...
js 新浏览器打开页面
博主gzh:“程序员野区”,回复“加群”,可进博主web前端微信群 效果如下 setTimeout(()>{var url "https://blog.csdn.net/xuelang532777032?typeblog"; //要打开的网页地址var features "height500, width800, top100, left100, …...
jmeter软件测试实验(附源码以及配置)
jmeter介绍 JMeter是一个开源的性能测试工具,由Apache软件基金会开发和维护。它主要用于对Web应用程序、Web服务、数据库和其他类型的服务进行性能测试。JMeter最初是为测试Web应用程序而设计的,但现在已经扩展到支持更广泛的应用场景。 JMeter 可对服务…...
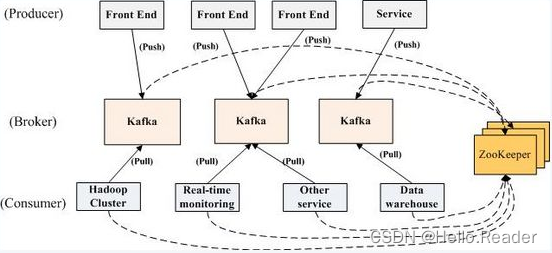
ZooKeeper原理剖析
1.ZooKeeper简介 ZooKeeper是一个分布式、高可用性的协调服务。在大数据产品中主要提供两个功能: 帮助系统避免单点故障,建立可靠的应用程序。提供分布式协作服务和维护配置信息。 2.ZooKeeper结构 ZooKeeper集群中的节点分为三种角色:Le…...

【算组合数】CF1833 F
少见地秒了这道1700,要是以后都这样就好了.... Problem - F - Codeforces 题意: 给定一个数列,让你在这个数列里找一个大小为M的子集,使得极差不超过M 思路: 子集,不是子序列,说明和顺序无…...
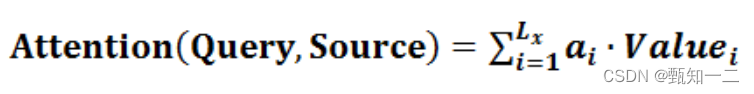
Attention详解(自用)
encoder-decoder 分心模型:没有引入注意力的模型在输入句子比较短的时候问题不大,但是如果输入句子比较长,此时所有语义完全通过一个中间语义向量来表示,单词自身的信息已经消失,可想而知会丢失很多细节信息࿰…...

pptx转pdf工具类
引入依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>5.0.0</version></dependency><dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxm…...

2023华为OD统一考试(B卷)题库清单(持续收录中)以及考点说明
目录 专栏导读2023 B卷 “新加题”(100分值)2023Q2 100分2023Q2 200分2023Q1 100分2023Q1 200分2022Q4 100分2022Q4 200分牛客练习题 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷)》。 刷的越多&…...
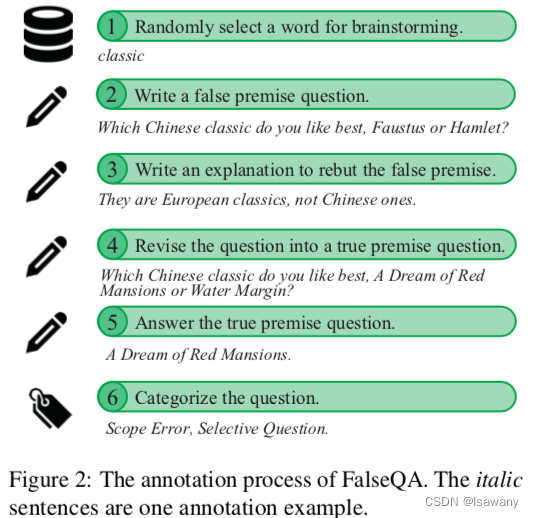
论文笔记--Won’t Get Fooled Again: Answering Questions with False Premises
论文笔记--Won’t Get Fooled Again: Answering Questions with False Premises 1. 文章简介2. 文章概括3 文章重点技术3.1 大模型面对FPQs的表现3.2 False QAs数据集3.3 训练和评估 4. 文章亮点5. 原文传送门 1. 文章简介 标题:Won’t Get Fooled Again: Answerin…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
