C—数据的储存(下)
文章目录
- 前言
- 🌟一、练习一下
- 🌏1.例一
- 🌏2.例二
- 🌏3.例三
- 🌏4.例四
- 🌟二、浮点型在内存中的储存
- 🌏1.浮点数
- 🌏2.浮点数存储
- 💫(1).二进制浮点数
- 💫(2).浮点数的存储规定
- 💫(3).浮点数的取出规定
- 🌏3.例题
- 😽总结
前言
👧个人主页:@小沈熬夜秃头中୧⍤⃝❅
😚小编介绍:欢迎来到我的乱七八糟小星球🌝
📋专栏:C语言学习
🔑本章内容:C-数据的储存(下)
送给各位💌:学无止境
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~
🌟一、练习一下
🌏1.例一
看过C语言学习第十五弹后我们一起来做一下下面这道例一
#include<stdio.h>
#include<windows.h>
int main()
{unsigned int i;for (i = 9; i >= 0; i--){printf("%u\n", i);Sleep(1000);//单位毫秒}return 0;
}
答案:死循环
解析:因为这是一个无符号int 类型的i所以当i=0再- -时,成为-1,但是无符号整形中没有符号位所以就变成了一个很大的数一直打印这个条件恒成立,所以就死循环了

🌏2.例二
看过例一我们来做一下例二:
#include<stdio.h>
#include<windows.h>
int main()
{unsigned int i;for (i = 9; i >= 0; i--){printf("%d\n", i);Sleep(1000);//单位毫秒}return 0;
}
答案:死循环
解析:虽然这是一个无符号整形i,但是打印的时候用的%d(打印有符号整形的),所以它是由符号位的,但有人可能要问了-1不就不满足i>=0吗?别忘了i是一个我无符号整型只不过打印用的%d但这并不影响i是一个无符号整型所以判断的时候i>=0是根据无符号数判断的

🌏3.例三
#include<stdio.h>
int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d", strlen(a));return 0;
}
答案:255
解析:经过循环a[i]里面存的是-1 -2 -3…-127 -128但是char 类型所以不存在-129 -130…-1000,-128减去1,就变成了127 依次往后127 126 125…3 2 1 0,这才是256个数字了,所以接着循环3 2 1 0…-128 -127-126…127 …3 2 1 0直到数组填满但是strlen是求字符串的长度,找的是\0,\0的ASCII码值是0所以到第一次为0的时候就找到了长度是255.


🌏4.例四
#include<stdio.h>
unsigned char i = 0;
int main()
{for (i = 0; i <= 255; i++){printf("hello world\n");}return 0;
}
答案:死循环
解析:
因为无符号char的范围是0~255;所以当i=255是再++不会变成256因为会发生截断再次变成0由此造成死循环。下面是256的二进制位可以看到截断后二进制是00000000所以不会出现266,条件恒成立。


🌟二、浮点型在内存中的储存
🌏1.浮点数
浮点数的家族包括:float, double ,long double
浮点数表示范围:float.h中定义
🌏2.浮点数存储
💫(1).二进制浮点数
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数v可以表示成下面的形式:
(1). (-1)^S* M* 2^E
(2).(-1)^S表示符号位,当S=0,V为正数;当S1,为负数。M表示有效数字,大于等于1,小于2’。
(3).2^E表示指数位。
v = (-1)^ s * 2^E * M
举例来说:根据上述公式,5.5 怎么写呢?
解析:1111.1111,我们都知道二进制位每位都有权重,小数点前面的1权重是0依次往前就是0 1 2 3…;小数点后面的权重则是-1依次往后-1 -2 -3…;所以5.5的二进制可以写成101.1,小数点往前移可以写成1.011*2^2,前面的第一个2代表二进制而第二个2代表移动了两位;加上正负号,因为5.5是正数所以S=0,最终可以写成V=(-1) ^ 0 * 2 ^2 1.011.所以S=0;M=1.011;E=2
举例来说:那么5.0和-5.0怎么写呢?
解析:十进制的5.0,写成二进制是101.0,相当于1.01×2^2。那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是-101.0,相当于-1.01x2^2。那么,S=1,M=1.01,E=2。
举例来说:那么5.3怎写呢?
解析:十进制的5.3 写成二进制是不能精准由后面的数凑出来所以说不能精准保存
举例来说:那么0.5怎么写呢?
十进制的0.5,写成二进制是0.1(小数点后的第一位权重是-1所以相当于2^(-1)),也就是0.5,相当于1.0*2 ^(-1)。那么,按照上面V的格式,可以得出S=0,M=1.0,E=-1。
💫(2).浮点数的存储规定
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过,1<M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)这意味着,如果E为8位,它的取值范围为O~255;如果E为11位,它的取值范围为0-2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
float 32位的浮点型
double 64位的浮点型

也就是:例如5.5的存法
二进制:101.1
(-1)^ 01.011 * 2^2根据规定float类型E+127就变成了129;129的二进制序列10000001(E);M存的小数点后面的也就是(01100000000000000000000)再加上S中存储的0就变成了01000000101100000000000000000000转换成十六进制(四个二进制转换成一个十六进制位4 0 b 0 0 0 0 0

💫(3).浮点数的取出规定
然后,指数E从内存中取出还可以再分成三种情况:
(1).E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),有效数字M前加上第一位的1。
比如:
0.5 (1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2N(-1),其阶码为-1+127=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000
(2).E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示(±)0,以及接近于0的很小的数字。
(3).E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
🌏3.例题

解析:
以整数的视角,存放整型的数字
00000000000000000000000000001001-9的原反补相同;9(%d打印整形)
浮点数存储:
0(S) 00000000(E) 0000000000000000001001(M);E为全0,浮点数的指数E等于1-127(或者1-1023)即为真实值;E=1-127=-126;有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数M=0.0000000000000000001001
(-1)^ 0 * 0.00000000000000000010012^(-126)所以浮点数打印出来是0.000000
以浮点数的视角,存放浮点型的数字
二进制:1001.0
1.0012^3
(-1)^ 0 * 1.001 * 2^3
S=0;E=3;M=1.001*
01000001000100000000000000000000-正数原码反码补码相同%d打印出来是1091567616
😽总结
😽Ending,今天的C—数据的储存(下)内容就到此结束啦~,如果后续想了解更多,就请关注我吧,一键三连哦 ~
相关文章:

C—数据的储存(下)
文章目录 前言🌟一、练习一下🌏1.例一🌏2.例二🌏3.例三🌏4.例四 🌟二、浮点型在内存中的储存🌏1.浮点数🌏2.浮点数存储💫(1).二进制浮点数&#x…...

「软件测试面试干货」2023年软件测试面试题大全(持续更新)附答案..
先卖个关子,如果你是面试官,你希望招一个什么样的人进来? 如果这个问题搞明白了,那么可以说测试岗位的面试,就变得非常轻松了。 按照一般的惯例,面试官都会让你自我介绍,介绍你的项目经验&…...
YOLOv2论文对比总结
1、高分辨率图片效果提升 2、Anchor 3、Loss函数 4、小目标友好...
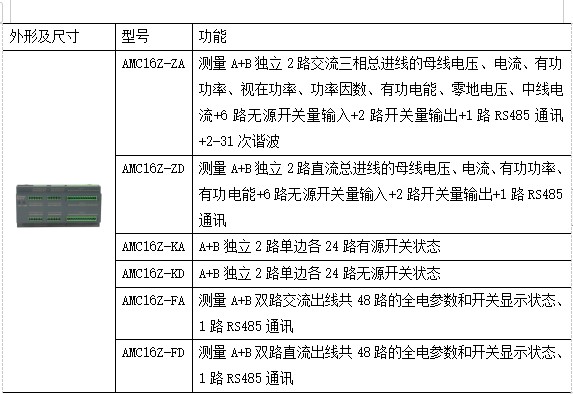
数据中心机房机柜配电新模式的探讨与选型
安科瑞 华楠 摘 要:对数据中心机房列头柜配电方式特征和问题进行深入研究,分析机房末端配电安全性及可用性,主要阐述了数据中心机房机柜配电新模式。 关键词:数据中心;机房机柜;配电模式 1 原始配电方案 …...

Redis未授权访问漏洞
前言 传统数据库都是持久化存储到硬盘中,所以执行某些业务时传统数据库并不是很理想。redis等数据存储在内存中的数据库就应允而生了。基于内存的Redis读速度是110000次/s,写速度是81000次/s 。但是基于内存的缺点就是断电即失,如果服务器产生了意外…...

Python 各种进制转换
def binary_to_decimal(binary_number):#2进制转换成10进制return int(binary_number, 2) def hex_to_decimal(binary_number):#hexadecimal #16进制转换成10进制return int(binary_number, 16) def octal_to_decimal(binary_number):#8进制转换成10进制return int(binary_numb…...
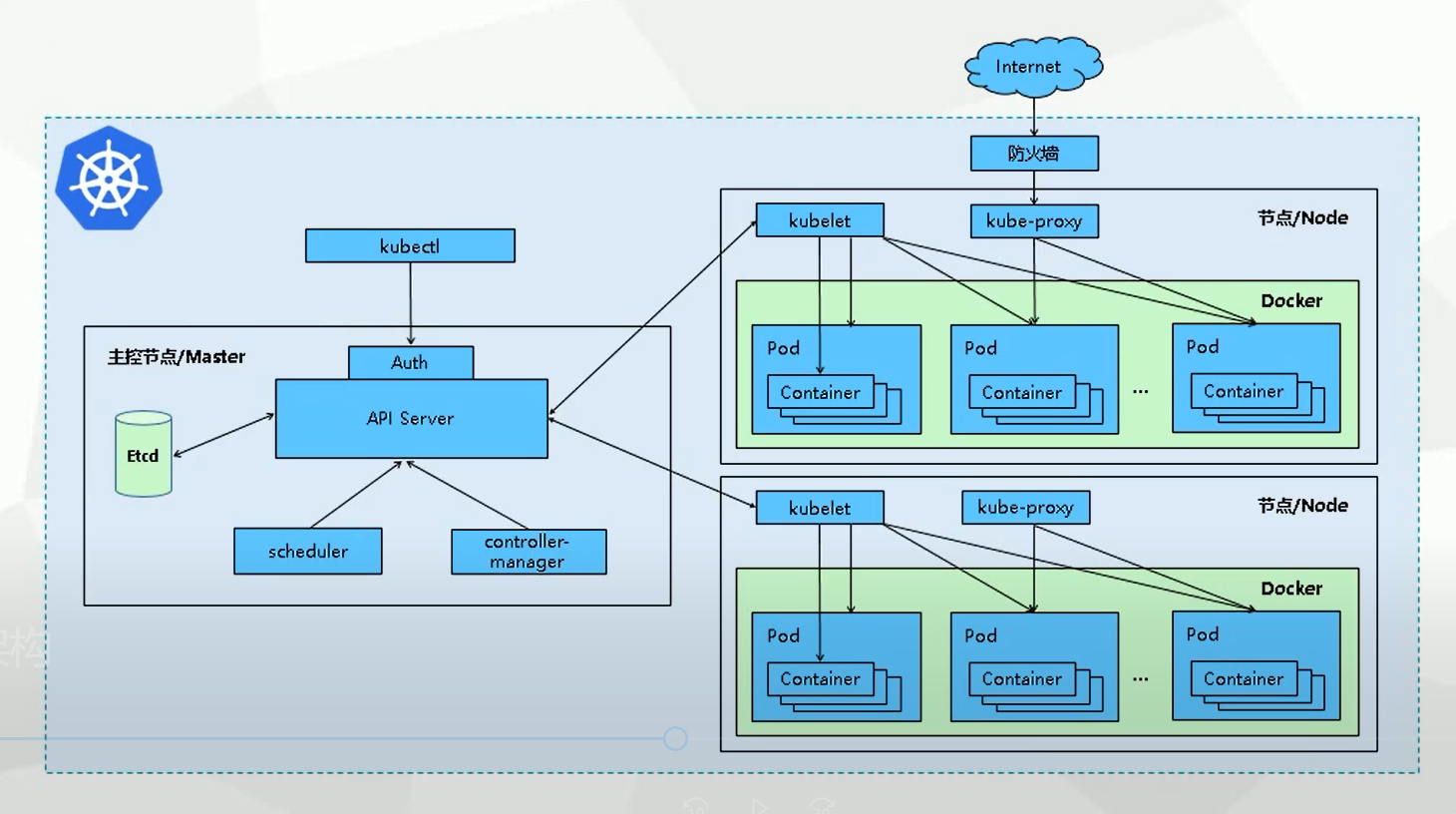
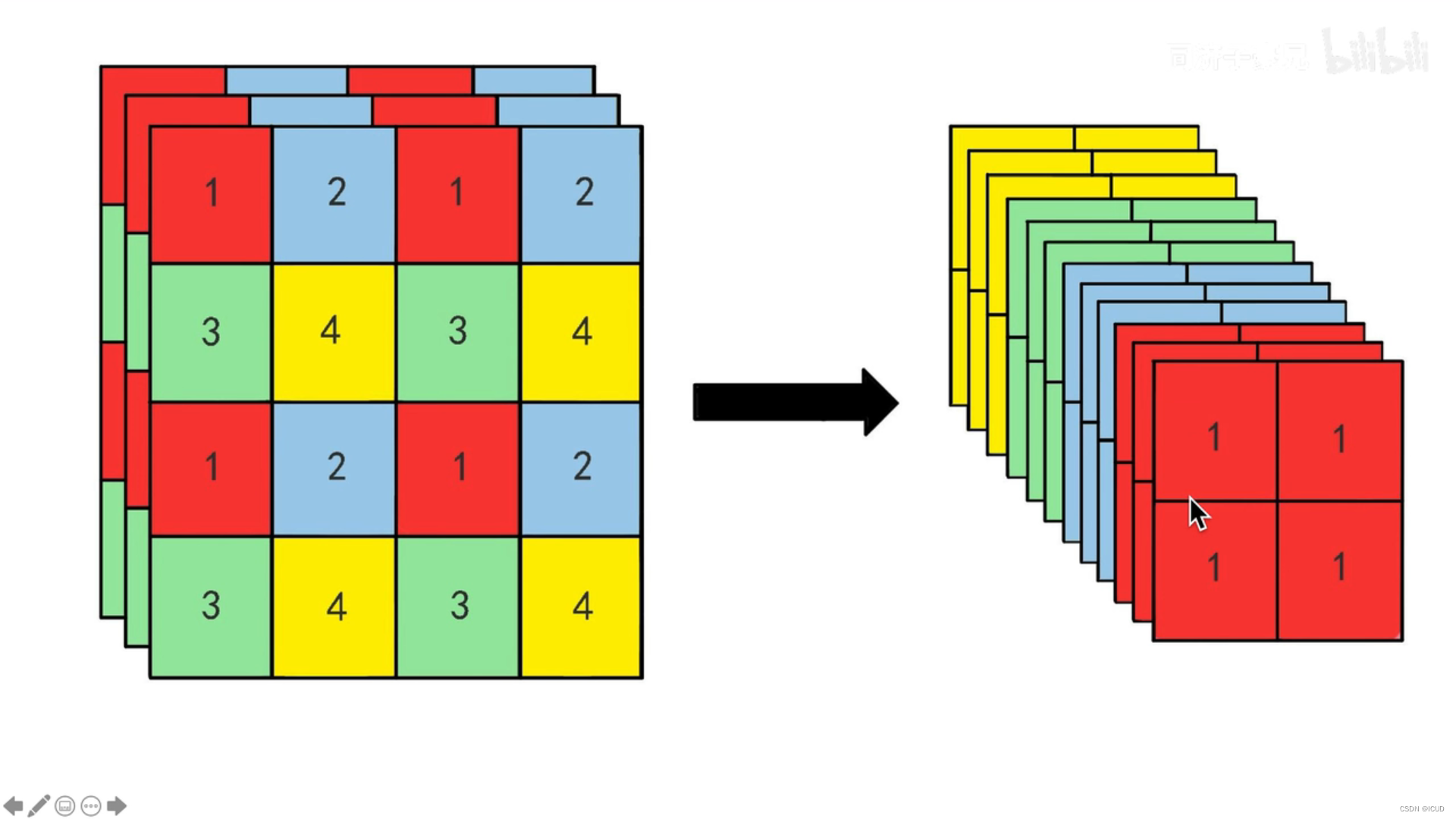
关于K8s的Pod的详解(一)
关于K8s的Pod的详解(一) Pod和API server的通信加快Pod启动更改Pod的资源Pod 的持久卷的单个访问模式Pod 拓扑分布约束Pod 拓扑分布中的最小域数 Pod 作为k8s创建,调度,管理的基本单位。由上级的Controller对Node上安装的Kubelet发…...

Vue3通透教程【十六】TS编译配置
文章目录 🌟 写在前面🌟 初始化配置文件⭐ target⭐ module⭐ lib⭐ types/node⭐ include⭐ outDir🌟 写在最后 🌟 写在前面 专栏介绍: 凉哥作为 Vue 的忠实 粉丝输出过大量的 Vue 文章,应粉丝要求开始更…...

OpenCV系列__chapter2
这里写目录标题 1 图像加减乘除位运算1.1 加法 img cv2.add(img1, img2)1.2 减法 img cv2.subtract(img1, img2)1.3 乘法 img cv2.multiply(img1, img2)1.4 除法 img cv2.divide(img1, img2)1.5 位运算 cv2.bitwise_and() 2 图像增强2.1 线性变换2.2 非线性变换 3 图像几何…...

Chat GPT是什么,初学者怎么使用Chat GPT,需要注意些什么
目录 Chat GPT是什么 初学者怎么使用Chat GPT 使用Chat GPT需要注意什么 一些简单的prompt示例 Chat GPT是什么 Chat GPT是由OpenAI开发的一种大型语言模型,它基于GPT(Generative Pre-trained Transformer)架构。GPT是一种基于深度学习的…...
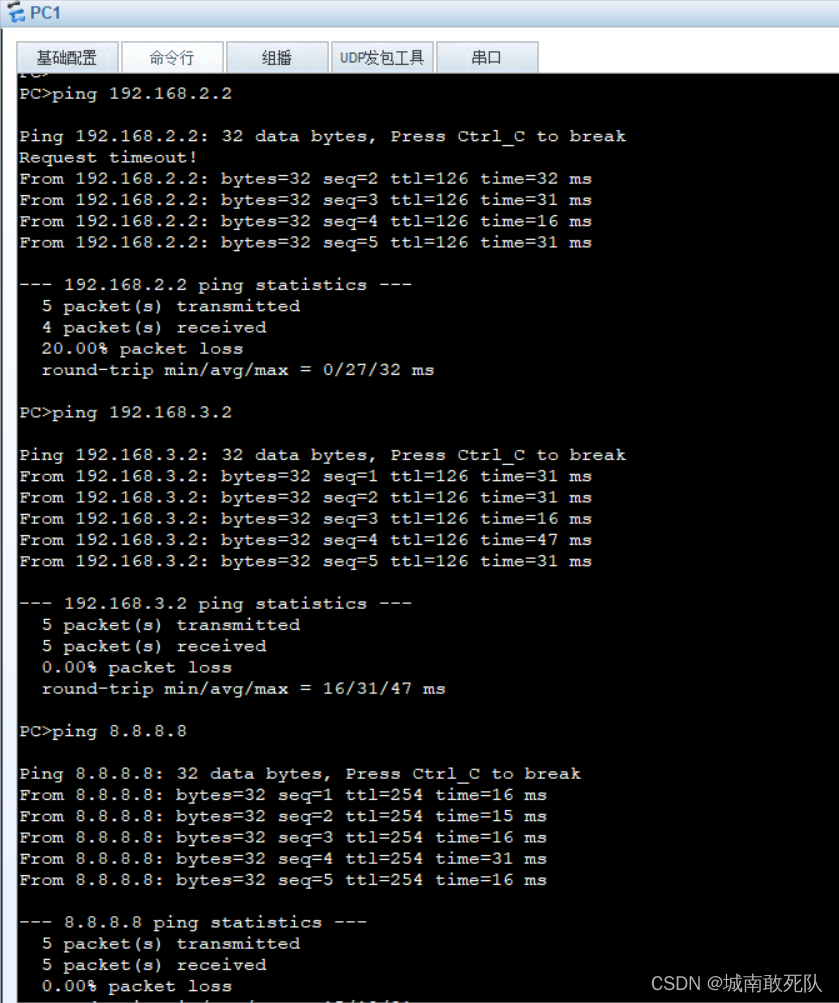
hcip mgre与rip实验
要求: 1.toop搭建 2.IP地址规划 R1g 0/0/1 192.168.1.1 24 s 4/0/0 188.0.0.2 24 t:10.0.0.1 24R2 s 4/0/0 188.0.0.1 24 s 4/0/1 188.0.1.1 24 s 3/0/0 188.0.2.1 24 loop0 8.8.8.8 24 t:10.0.0.2 24 R3g…...

骨传导耳机对身体有没有别的危害?骨传导耳机有什么好处?
骨传导耳机对身体有没有别的危害? 在此之前,我们先了解一下骨传导的原理:骨传导就跟它的名字一样通过骨头传声,主要是借助头部颅骨传递到听觉中枢,这种传播方式省略了直接接触耳道和耳膜。打个比方,就是我们…...

c++11/c++98动态规划入门第5课,经典DP问题 --- 区间
第1题 取数问题 查看测评数据信息 有一排N个数,你和小明2个人玩游戏,每个人轮流从2端取数,每次可以从左或右取,不能从中间取。你取的所有的数的和是你的得分,小明取的所有的数的和是小明的得分。如果你先取&#x…...
vue中重新获取数据导致页面加长,要求在页面更新之后浏览器滚动条滚动到之前浏览记录的位置。以及获取当前页面中是哪个元素产生滚动条的方法。
目前的页面样式为: 代码是: <section id"detailSection"><el-tableref"multipleTable":data"logDetailList"style"width: 650px;margin:20px auto;"id"dialogDetail":show-header"fals…...
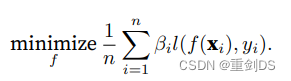
【深度学习】日常笔记14
对神经网络模型参数的初始化方案对保持数值稳定性有很重要的作用。初始化⽅案的选择可以与⾮线性激活函数的选择有趣的结合在⼀起。 突然有感触:做习题和模拟考研就分别是训练集和验证集,考研不就是最后的测试集() p168的↓的解释…...
[JAVAee]synchronized关键字
目录 1.synchronized的特性 ①互斥性 ②可重入性 2.synchronized的使用示例 ①修饰普通方法 ②修饰静态方法 ③修饰代码块 1.synchronized的特性 ①互斥性 互斥性,就像是给门上锁了一样. 当A线程使用了被synchronized修饰的代码块并对其上锁,其他线程(B线程,C线程)想要使…...

Unity游戏源码分享-3d机器人推箱子游戏
Unity游戏源码分享-3d机器人推箱子游戏 一个非常意思的3D游戏 工程地址:https://download.csdn.net/download/Highning0007/88098014...

SAAS部署模式
SAAS(Software as a Service)顾名思义,软件即服务的产品。 常见部署模式: 公有云:SAAS产品部署在公有云平台上,由SAAS提供商管理整个基础架构和应用程序。客户通过互联网访问和使用SAAS产品,无…...
11、PHP面向对象1
1、PHP的面向对象与其他语言类似,但也有不同。 PHP访问成员变量时,需要用“->”,而不能用“.”,访问成员函数时,需要用“->”,而不能用“.”。操作符“::”可以在没有任何声明实例的情况下访问类中的…...
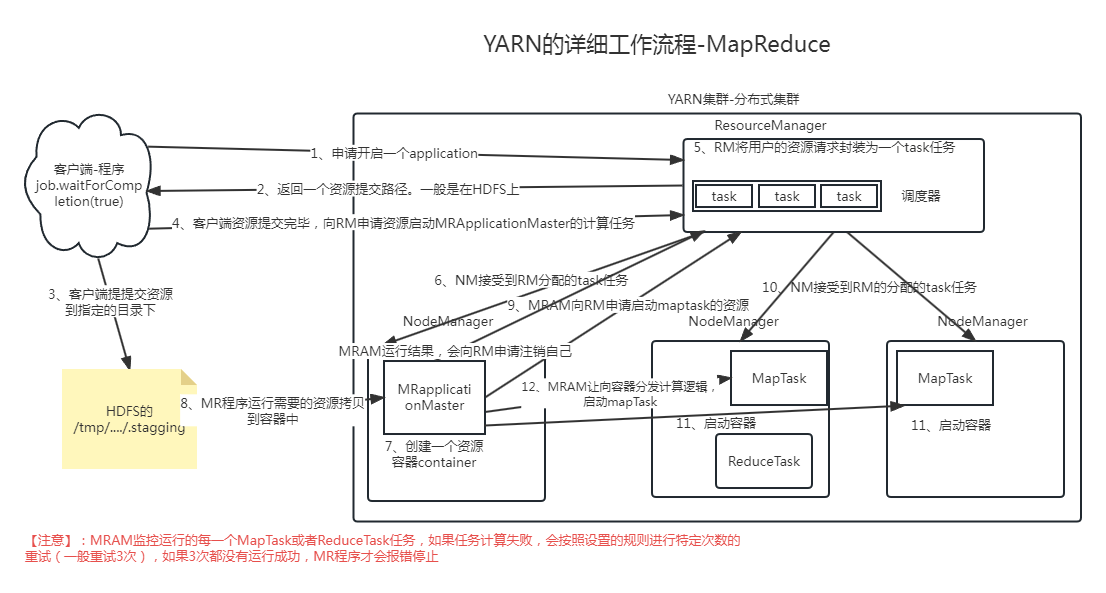
实训笔记7.25
实训笔记7.25 7.25笔记一、MapReduce的特殊使用场景1.1 通过MapReduce程序实现多文件Join操作1.1.1 通过在Reduce端实现join操作1.1.2 通过在Map端实现join操作 1.2 MapReduce中的计数器的使用1.2.1 计数器使用两种方式 1.3 MapReduce实现数据清洗 二、MapReduce的OutputFormat…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

