B/B+树算法
B树
基本概述
B树又称多路平衡搜索树。一棵m阶B树,要么是空树,要么满足以下特性:
- 每个节点最多有m棵子树
- 根节点至少有两棵子树
- 内部节点(除根和叶子节点以外的节点)至少有⌈m/2⌉棵子树
- 关键字个数比子树个数少1
- 终端节点(叶子节点)在同一层上,且不带任何信息(是空节点),通常称为失败节点
基本概念
B树的阶数为m,树高为h,关键字个数为k,节点个数为n。

阶是B树中,所有节点的子节点个数最大的那个数。如上图所示的树,其阶数为4。
树高是指树有几层,如上图,这个树就有2层,树高也就为2。
关键字个数,如上图,关键字个数为11
节点个数,如上图,节点个数为5
每个关键字头部指向所有比它小的关键字,尾部指向所有比它大的关键字
B树的排序
B树是有排序的,对应一个排序数组。
在具有k个关键字的B树中,查找失败有k+1种情况,且均为叶子节点。
最小树高和最小节点数
要让树高最小,那么每层的节点个数就要最大,即每个节点的子节点个数要最大,而m阶B树,其子节点的个数最大为m,那么我们让每个节点的子节点个数都为m,这样就能推导出最小树高。
| 第X层 | 节点个数 |
|---|---|
| 0 | 1 |
| 1 | m |
| 2 | m^2 |
| 3 | m^3 |
| … | … |
| h - 1 | m^(h-1) |
| h | m^h |
失败节点个数为mh,则mh = k + 1
即:
h >= log(k + 1)
最小节点数:
n = k / (m - 1)
最大树高与最大节点数
与上面最小类似,最大只有让每个节点的子节点个数最小就好。
| 第X层 | 节点个数 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 2⌈m / 2⌉ |
| 3 | 2⌈m / 2⌉^2 |
| … | … |
| h - 1 | 2⌈m / 2⌉^(h-2) |
| h | 2⌈m / 2⌉^(h-1) |
2⌈m / 2⌉^(h-1) = k + 1
所以:
h≤log_⌈m/2⌉ ((k+1)/2)+1
根节点最少可以只有1个关键字,而其他节点最少需要⌈m/2⌉-1个关键字。考虑根节点补齐到⌈m/2⌉-1个关键字,则总关键字个数k需要增加⌈m/2⌉-2个。因此最大节点数为:
n≤(k+⌈m/2⌉-2)/(⌈m/2⌉-1)
B+树
B树中,每个节点都存有key-value,为了节省存储空间,可以采用B+树,在每个节点中,仅存储key即可。
B树有两种结构:

其中第2中结构比第一种结构更节省空间,且与B树更相似,因此也主要以第2种结构为主。第2种结构B+树的特征与B树相似,差别为:最后一层非叶子节点包含了全部的关键字,且节点间按升序顺序连接。
相关文章:

B/B+树算法
B树 基本概述 B树又称多路平衡搜索树。一棵m阶B树,要么是空树,要么满足以下特性: 每个节点最多有m棵子树根节点至少有两棵子树内部节点(除根和叶子节点以外的节点)至少有⌈m/2⌉棵子树关键字个数比子树个数少1终端节…...
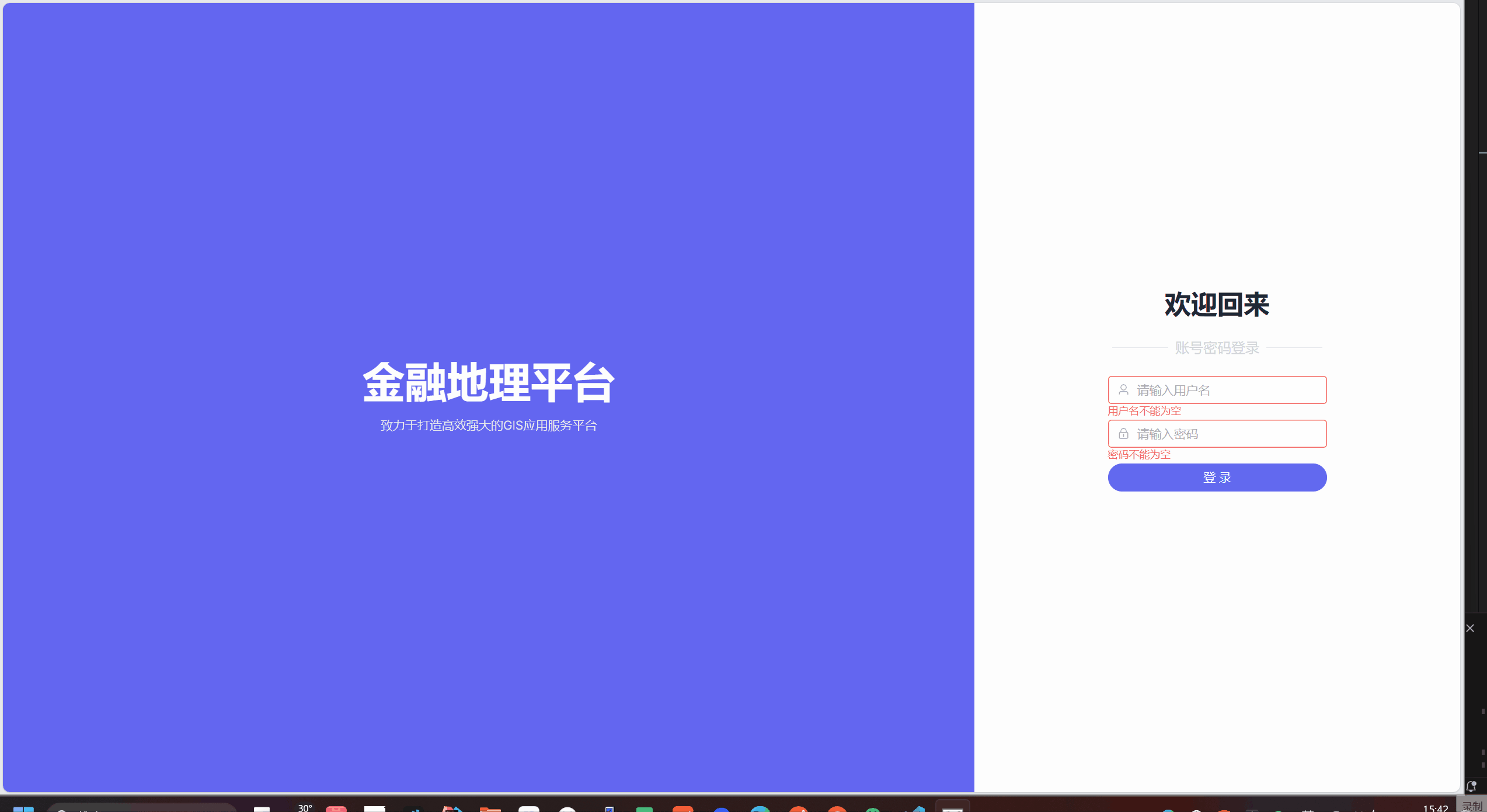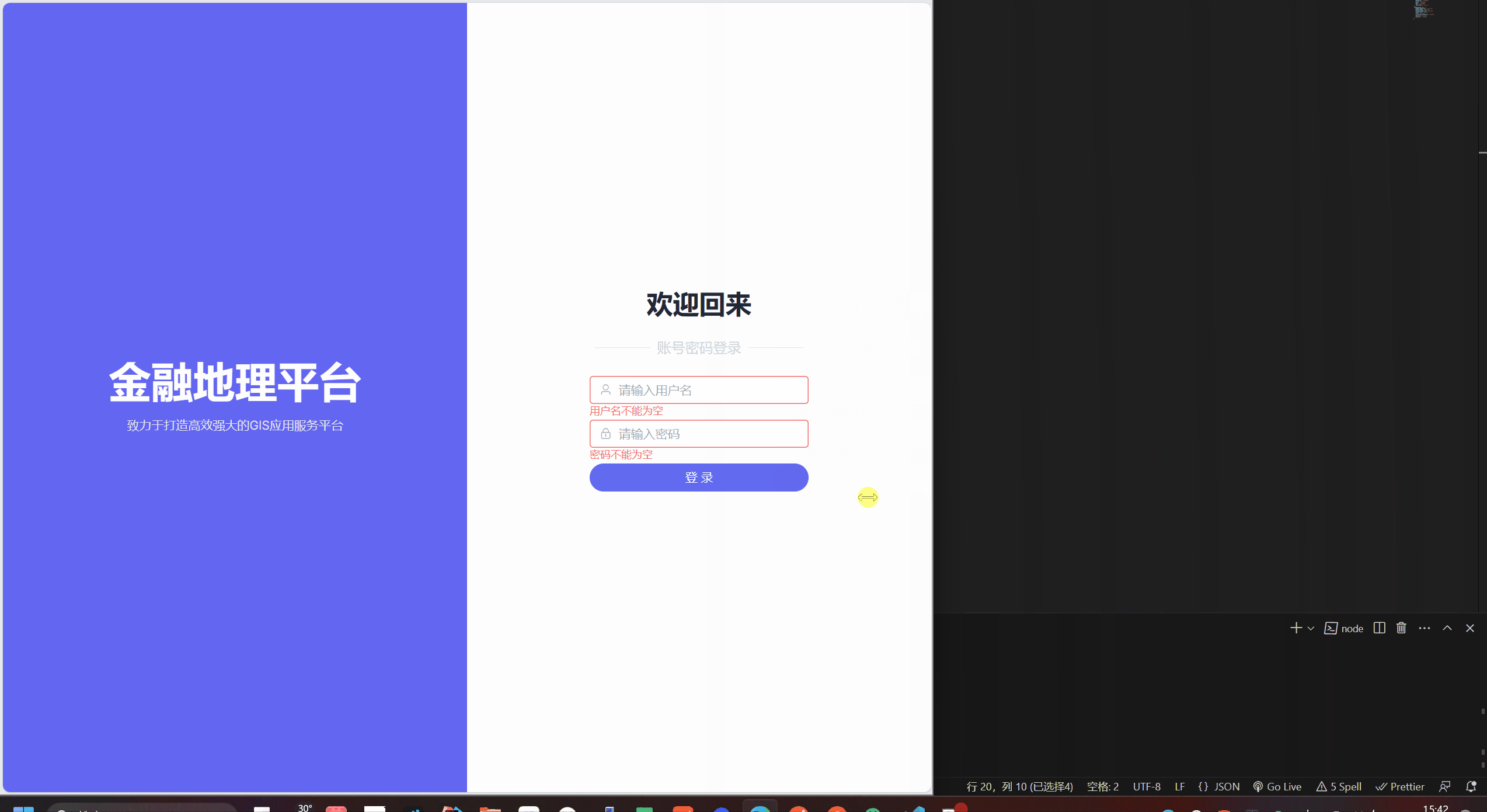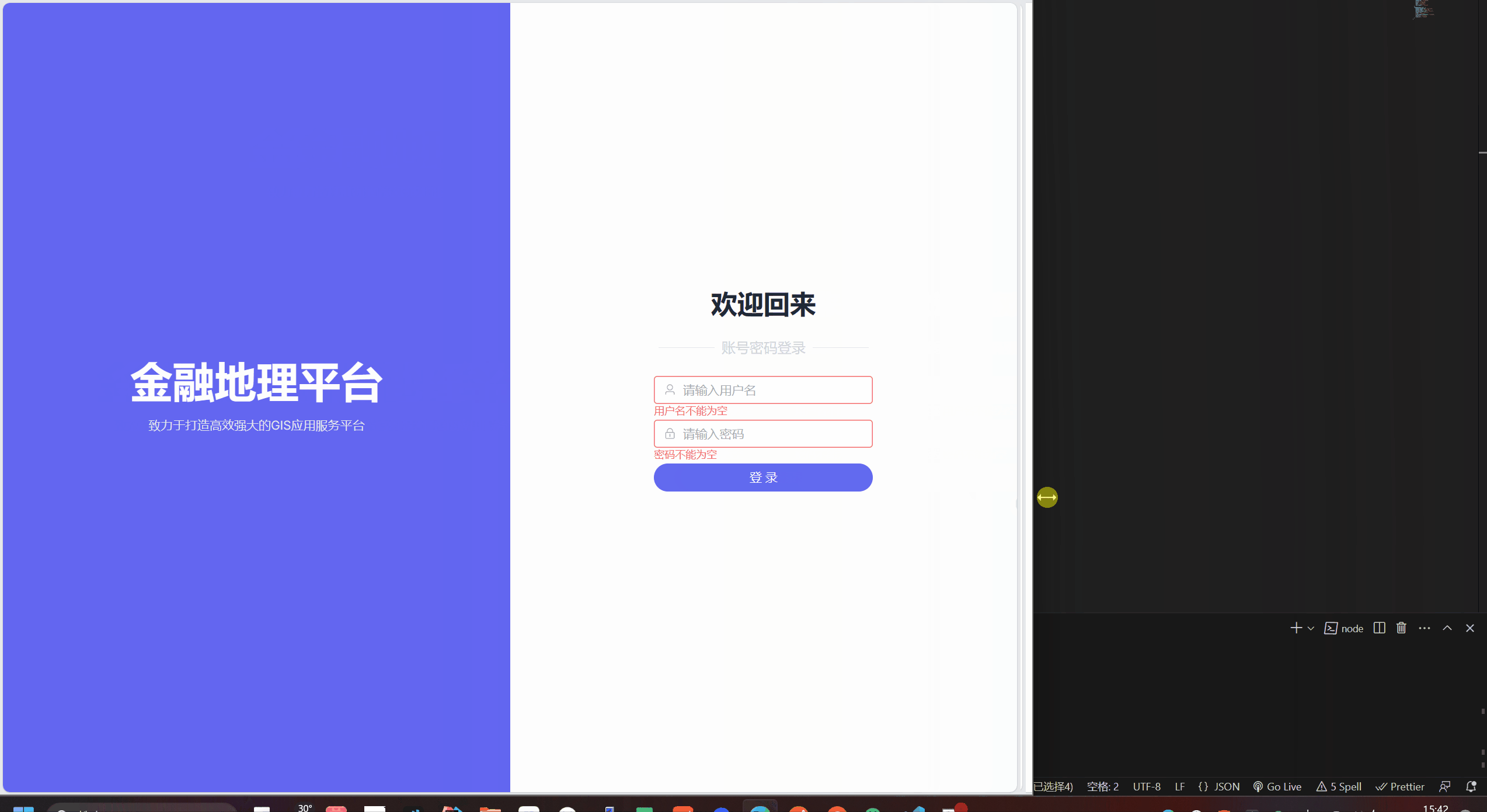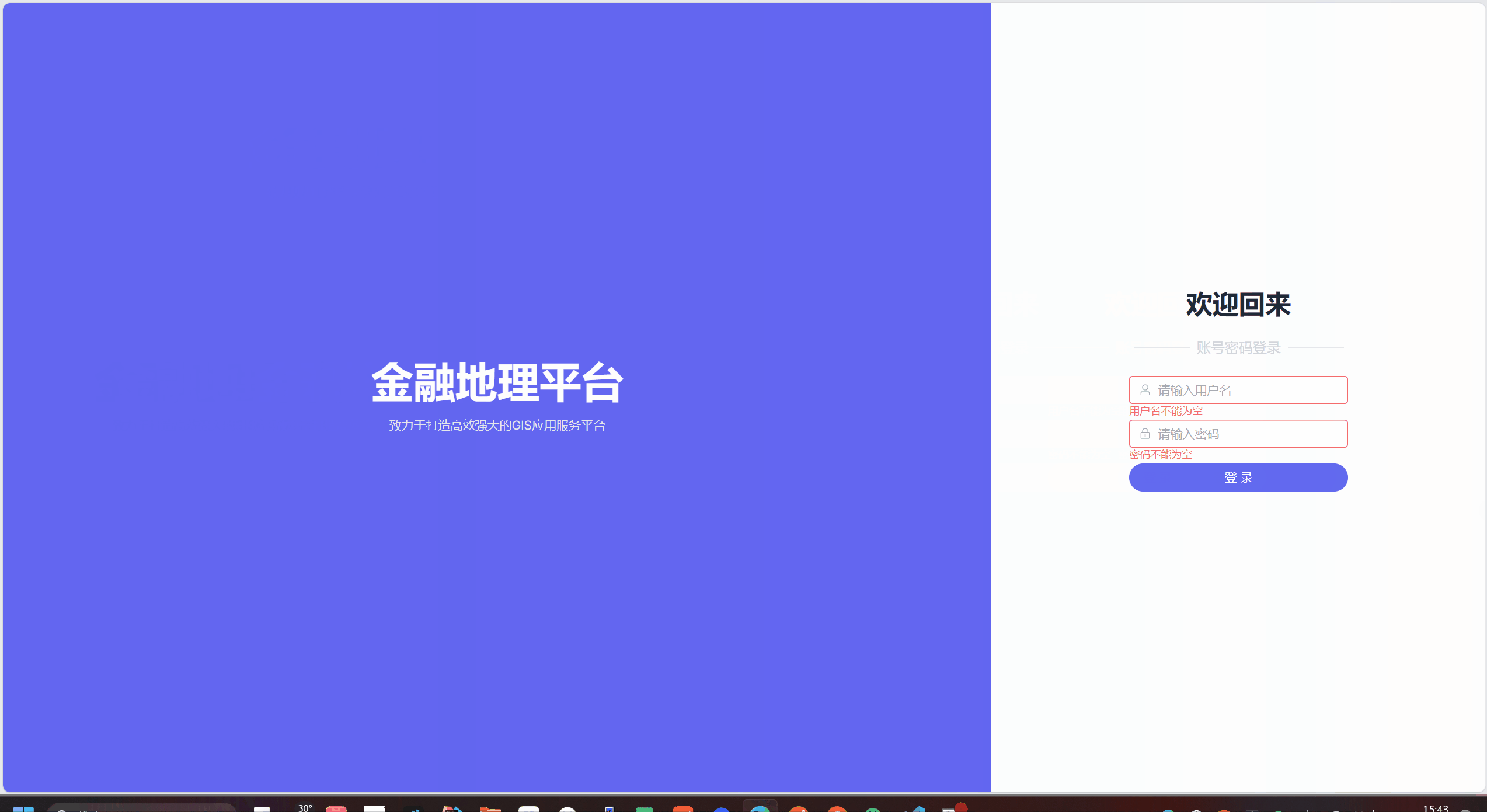
vue3.2 + elementPlus + Windi CSS + ts创建一个好用的可兼容不同宽高的login页面
1.效果预览 2. 代码准备 导入windiCSS: npm i -D vite-plugin-windicss windicss windiCSS官网: https://cn.windicss.org/integrations/vite.html 使用vite创建好你的vue工程 sass版本为: 1.49.9 3.Windi CSS在页面中使用 apply 二次定义类名…...
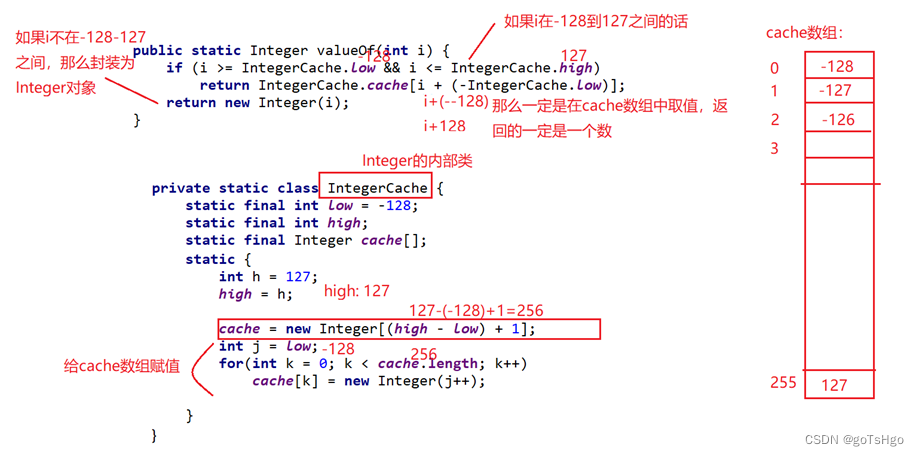
Integer包装类详解加部分源码
【1】Java.lang直接使用,无需导包: 【2】类的继承关系: 【3】实现接口: Serializable,Comparable<Integer> 【4】这个类被final修饰,那么这个类不能有子类,不能被继承: 【5】…...

如何给侧边栏添加 Badge 计数标记
一、需求功能 给侧边菜单栏或及子菜单栏添加计数标记 el-badge 效果如下: 二、实现思路 结合 icon 图标渲染的思路,通过在layout 的 item.vue 中使用 vnodes.push 方法实现对 <el-badge /> 的渲染。在通过 Vuex 的状态管理将菜单栏需要的数据转…...

插槽slot复习
1.认识插槽 ◼ 在开发中,我们会经常封装一个个可复用的组件: 前面我们会通过props传递给组件一些数据,让组件来进行展示; 但是为了让这个组件具备更强的通用性,我们不能将组件中的内容限制为固定的div、span等等…...

【C++STL标准库】序列容器之deuqe与、orwa_list与list
基本概念这里就不再浪费时间去解释,这里给出deuqe与、orwa_list、list的基本使用方法: deque队列: #include <iostream> #include <deque>template <typename T> void print(T Begin, T End);int main() {std::deque<…...
-功能特性-消息发送重试和流控机制)
RocketMQ教程-(5)-功能特性-消息发送重试和流控机制
本文为您介绍 Apache RocketMQ 的消息发送重试机制和消息流控机制。 背景信息 消息发送重试 Apache RocketM Q的消息发送重试机制主要为您解答如下问题: 部分节点异常是否影响消息发送? 请求重试是否会阻塞业务调用? 请求重试会带来什…...

OpenCV笔记
opencv读取视频操作 import cv2video cv2.VideoCapture("./1.mp4")if video.isOpened():# video.read() 一帧一帧地读取# open 得到的是一个布尔值,就是 True 或者 False# frame 得到当前这一帧的图像open, frame video.read() else:open Falsewhile …...

Mysql基础(下)之函数,约束,多表查询,事务
👂 回到夏天(我多想回到那个夏天) - 傲七爷/小田音乐社 - 单曲 - 网易云音乐 截图自 劈里啪啦 -- 黑马Mysql,仅学习使用 👇原地址 47. 基础-多表查询-表子查询_哔哩哔哩_bilibili 目录 🦂函数 dz…...

Android 屏幕适配各种宽高比的手机
由于android 手机的屏幕宽高比样式太多了,在设计UI时,很多时候,会因为宽高比,分辨率不同会有展示上的差异。 我是这样解决的 在activity的onCreate方法前,调用: fun screenFit(context: Context) {val me…...
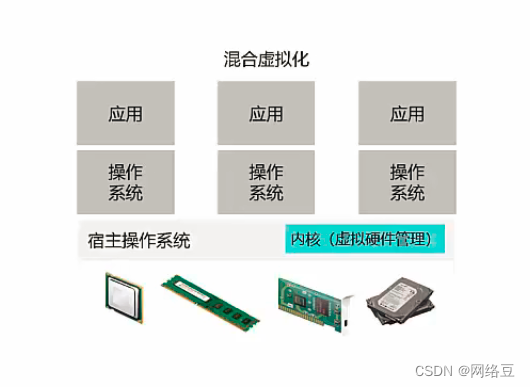
云计算——云计算与虚拟化的关系
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.虚拟化 1.什么是虚拟化 2.虚拟化技术作用 二.云计算与虚拟化的关系 三.虚…...

手机变局2023:一场瞄准产品和技术的“思维革命”
以折叠屏冲高端,已成为中国手机厂商们的共识。 在这个苹果未涉足的领域,国产手机厂商们加快脚步迭代推新,积极抢占机遇。但平心而论,虽然国产折叠屏机型众多,但市场上始终缺乏一款突破性的产品作为标杆,为…...
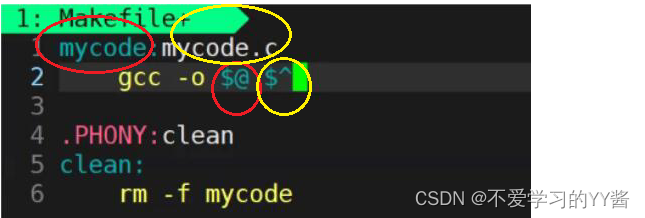
【Linux】自动化构建工具-make/Makefile详解
前言 大家好吖,欢迎来到 YY 滴 Linux系列 ,热烈欢迎!本章主要内容面向接触过Linux的老铁,主要内容含 欢迎订阅 YY 滴Linux专栏!更多干货持续更新!以下是传送门! 订阅专栏阅读:YY的《…...

1 js嵌入html使用
1.1 直接在html内部使用js代码 使用script标签,在前后标签内部写的代码即为js代码。 <body><p id"p1">初始段落</p> <!--id是为了定位需要更改内容的标签--><button type"button" onclick"showNum()">…...

总结RoctetMQ
RoctetMQ 定义优缺点场景使用方式消息顺序问题死信幂等性可视化面板 定义 优缺点 场景 使用方式 消息顺序问题 死信 幂等性 可视化面板...

命名约定~
1.变量的命名约定 JavaScript 变量名称是区分大小写的,大写和小写字母是不同的。比如: let DogName Scooby-Doo; let dogName Droopy; let DOGNAME Odie; console.log(DogName); // "Scooby-Doo" console.log(dogName); // "Dro…...
和元组(tuple))
Python基础-列表(list)和元组(tuple)
Python包含6种内建的序列:列表,元组,字符串,Unicode字符串,buffer对象,xrange对象,本文讨论列表和元组。 1.列表可以修改,元组则不能修改。 2.几乎在所有的情况下,列表…...

Dubbo介绍及使用
🍓 简介:java系列技术分享(👉持续更新中…🔥) 🍓 初衷:一起学习、一起进步、坚持不懈 🍓 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正🙏 🍓 希望这篇文章对你有所帮助,欢…...

初阶C语言-分支和循环语句(下)
“花会沿途盛开,以后的路也是。” 今天我们一起来继续学完分支语句和循环语句。 分支和循环 3.循环语句3.4 do...while()循环3.4.1 do语句的用法 3.5关于循环的一些练习3.6 goto语句 3.循环语句 3.4 do…while()循环 3.4.1 do语句的用法 do循环语句;//当循环语句…...

pytorch工具——pytorch中的autograd
目录 关于torch.tensor关于tensor的操作关于梯度gradients 关于torch.tensor 关于tensor的操作 x1torch.ones(3,3) xtorch.ones(2,2,requires_gradTrue) print(x1,\n,x)yx2 print(y) print(x.grad_fn) print(y.grad_fn)zy*y*3 outz.mean() print(z,out)注意 atorch.randn(2,…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
