【图论】二分图
二分图,即可以将图中的所有顶点分层两个点集,每个点集内部没有边
判定图为二分图的充要条件:有向连通图不含奇数环
1、染色法
可以解决二分图判断的问题
步骤与基本思路
遍历图中每一个点,若该点未被染色,则遍历该点所相邻的点,相邻的点中未被染色的进行染色操作,已被染色的判断颜色是否合法,合法继续遍历,不合法退出
染色法板子
bool flag = true;
for (int i = 1; i <= n; i ++ )
{if (!color[i]) // 未被染色则开始遍历{if (!dfs(i, 1)){flag = false;break;}}
}bool dfs(int u, int c)
{color[u] = c; // 对该点进行染色for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (!color[j]) // 未被染色的点进行染色{if (!dfs(j, 3 - c)) return false;}else if (color[j] == c) return false; // 已染色的点判断是否合法}return true;
}2、匈牙利算法
可以解决最大匹配数的问题,也就是二分图的两个点集可以连多少条一一对应的边
步骤与基本思路
(1)遍历第一个点集的所有点,每个点遍历之前要记得把第二个点集的状态清空
(2)依次遍历这些点相邻的点,若该点未被遍历过,则判断该点是否满足未与前面的点匹配过或前面与它匹配的点有其他的匹配方案,若满足任意条件则让现在的两点匹配,不满足则说明当前第一个点集的这个点没有匹配对象
匈牙利算法板子
for (int i = 1; i <= n1; i ++ )
{memset(st, false, sizeof st); // 清空第二个点集的状态if (find(i)) res ++ ;
}bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]) // 若该点未被遍历过{st[j] = true;// 该点是否满足 未被匹配过 or 匹配的第一个点集的点有其他成功匹配方案if (match[j] == 0 || find(match[j])){match[j] = x; // 匹配现在的这两点return true;}}}return false;
}相关文章:

【图论】二分图
二分图,即可以将图中的所有顶点分层两个点集,每个点集内部没有边 判定图为二分图的充要条件:有向连通图不含奇数环 1、染色法 可以解决二分图判断的问题 步骤与基本思路 遍历图中每一个点,若该点未被染色,则遍历该…...
数据结构——(一)绪论
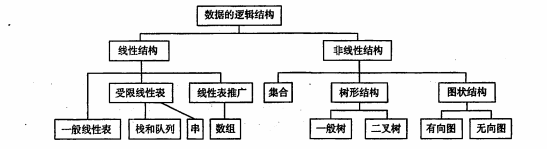
👉数据元素整体思维导图 欢迎补充 一、基本概念❤️ 1.1基本术语⭐️ (1)数据 客观事务属性的数字、字符。 (2)数据元素 数据元素是数据的基本单位,一个数据元素可由若干数据项组成,数据项是…...
[ 华为云 ] 云计算中Region、VPC、AZ 是什么,他们又是什么关系,应该如何抉择
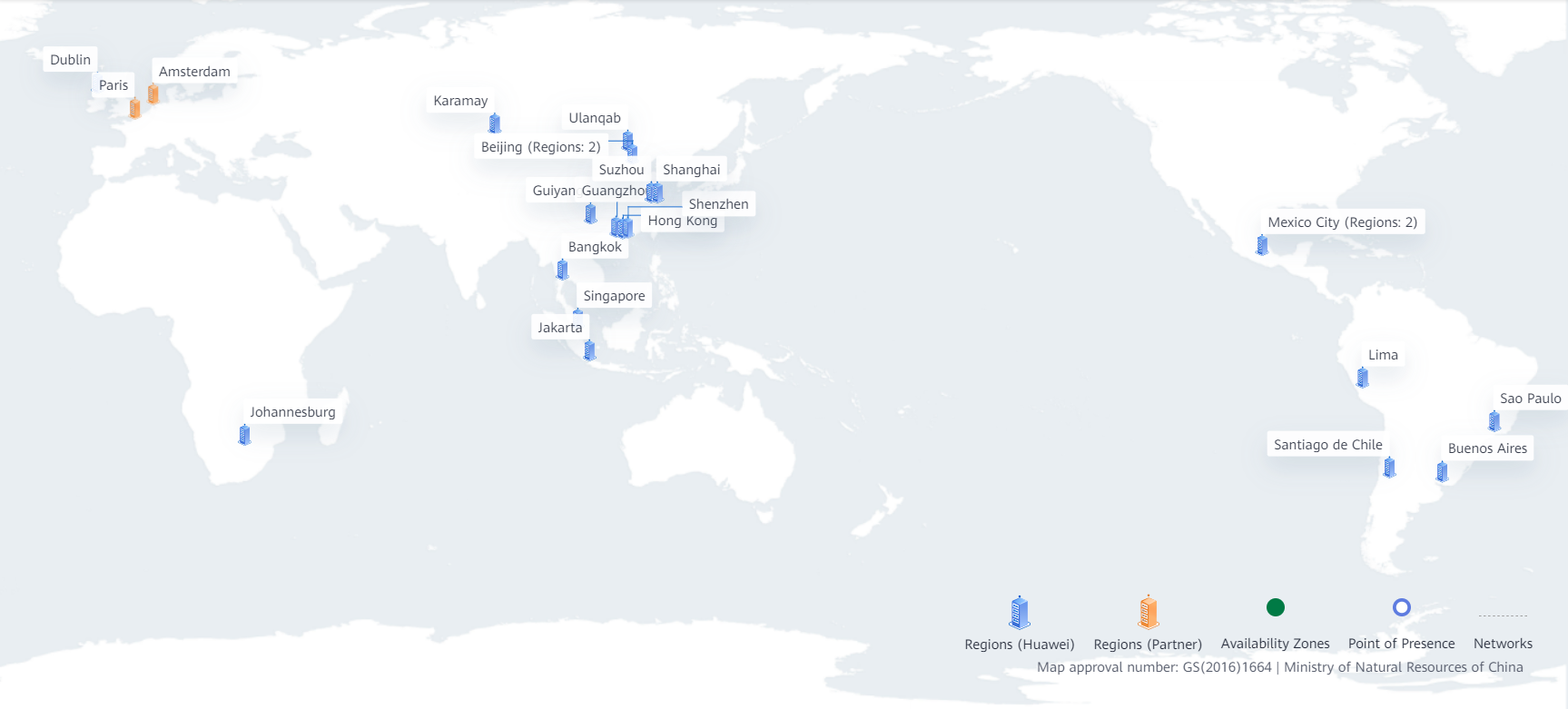
前几天看到一个问答帖,我回答完了才发现这个帖子居然是去年的也没人回复,其中他问了一些华为云的问题,对于其中的一些概念,这里来总结讲解一下,希望对学习华为云的小伙伴有所帮助。 文章目录 区域(Region&a…...

表单验证:输入的字符串以回车分隔并验证是否有
公司项目开发时,有一个需求,需要对输入的字符串按回车分隔并验证是否有重复项,效果如下: 表单代码: <el-form-item label"IP地址条目:" prop"ipAddressEntry"><el-inputtype&…...

智能财务分析-亿发财务报表管理系统,赋能中小企业财务数字化转型
对于许多中小企业来说,企业重要部门往往是财务和业务部门。业务负责创收,财务负责控制成本,降低税收风险。但因管理机制和公司运行制度的原因,中小企业往往面临着业务与财务割裂的问题,财务数据不清晰,无法…...

图为科技T501赋能工业机器人 革新传统工业流程
工业机器人已成为一个国家制造技术与科技水平的重要衡量标准,在2019年,中国工业机器人的组装量与产量均位居了全球首位。 当前,工业机器人被广泛用于电子、物流、化工等多个领域之中,是一种通过电子科技和机械关节制作出来的智能机…...
安全狗深度参与编写的《云原生安全配置基线规范》正式发布!
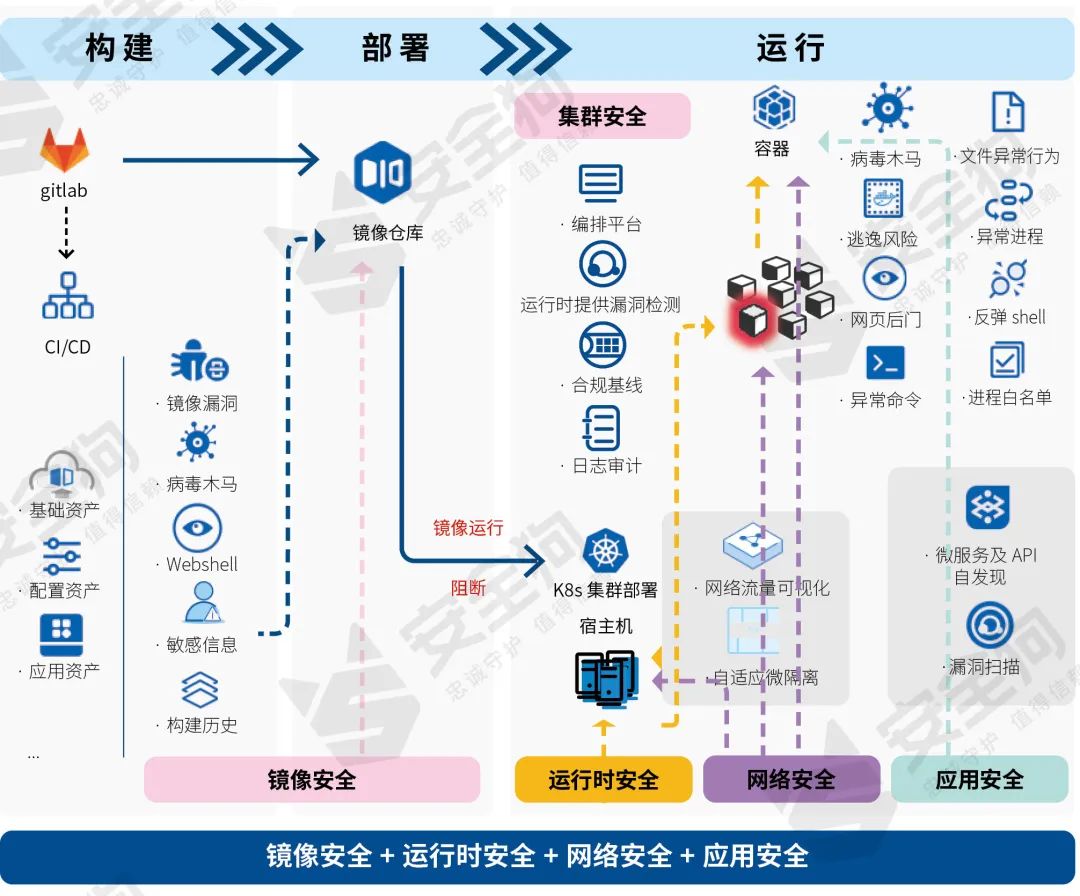
7月25日,由中国信息通信研究院、中国通信标准化协会主办的2023可信云大会在北京顺利开幕。 作为国内云原生安全领导厂商,安全狗受邀出席此次活动。 厦门服云信息科技有限公司(品牌名:安全狗)成立于2013年,…...
如何在3ds max中创建可用于真人场景的巨型机器人:第 2 部分
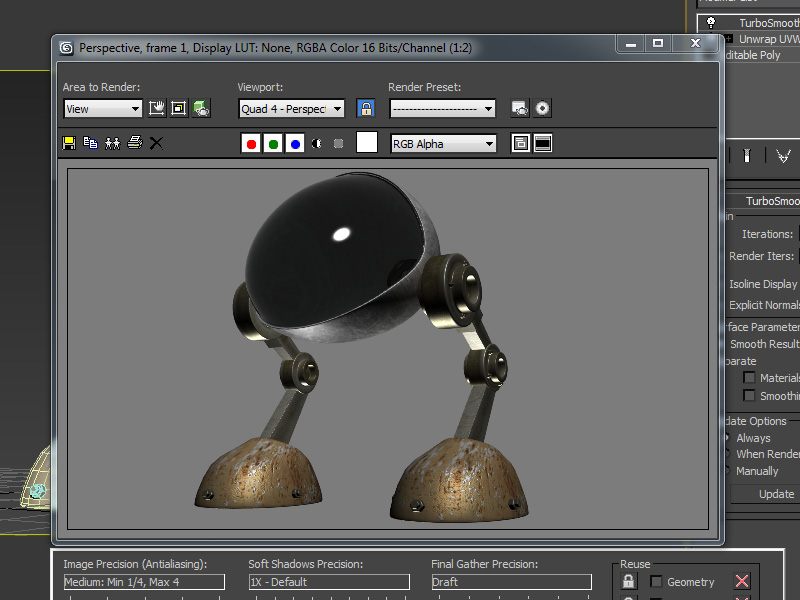
推荐: NSDT场景编辑器助你快速搭建可二次开发的3D应用场景 1. 创建主体 步骤 1 打开 3ds Max。选择机器人头部后,二次单击鼠标并选择隐藏未选中。机器人的其他部分 除了头部之外,将被隐藏。 打开 3ds Max 步骤 2 在人脸选择模式下&#x…...
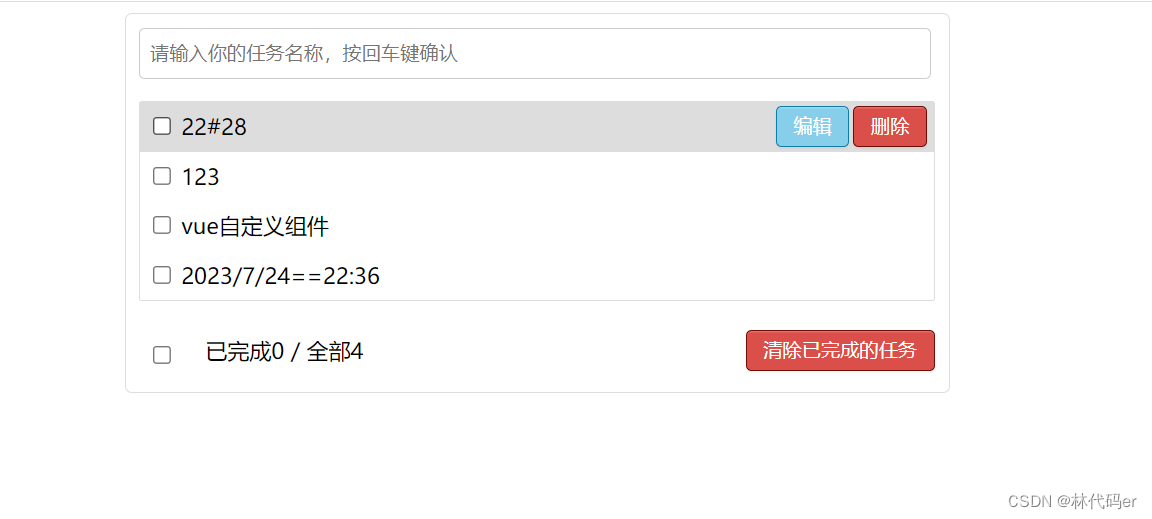
Vue中TodoList案例_编辑
nextTick: MyItem.vue 加一个编辑按钮,input框:blur失去焦点时触发事件handleBlur,ref获取真实dom: <inputtype"text"v-show"todo.isEdit":value"todo.title"blur"handleBlur(todo,$even…...
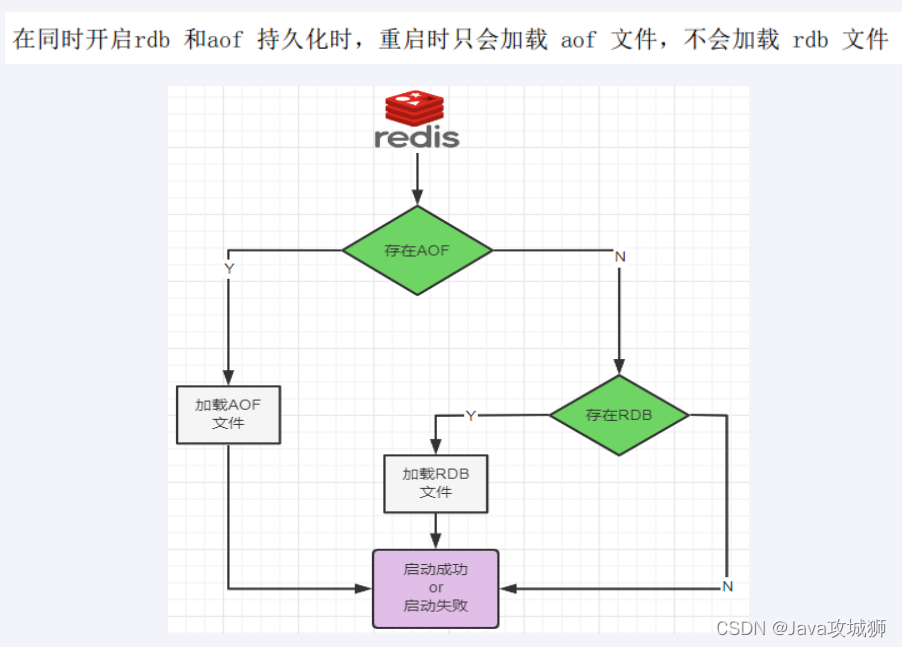
什么是Redis?
什么是Redis 什么是Redis一、特性1. 支持多种数据结构2. 读/写速度快,性能高。3. 支持持久化。4. 实现高可用主从复制,主节点做数据副本。5. 实现分布式集群和高可用。 二、基本数据类型string(字符串)list(双向链表)set(集合)zse…...

深入浅出理解vue2/vue3响应式原理
一、简介 当谈论Vue 2和Vue 3的响应式原理时,我们主要关注的是其数据双向绑定的机制。数据双向绑定是指当数据发生变化时,视图会自动更新;反之,当视图发生变化时,数据也会相应地更新。这种特性让我们在前端开发中更加…...

ssh连接服务器配置
平常每次都是 ssh root111.111.111.111 然后再输入密码 很事麻烦 总结 首先本地生成密钥和公钥 ssh-keygen -t rsa -C "XXX" ~/.ssh id_rsa.pub 将公钥加入远程服务器中的authorized_keys中 用户可以手动编辑该文件,把公钥粘贴进去,也可…...

el-table 表头设置渐变色
<el-table :data"tableData" stripe><el-table-column prop"name" label"测试" align"left"></el-table-column><el-table-column prop"code" label"测试1" align"left"></…...

GB/T 25000.51解读——软件产品的易用性怎么测?
GB/T 25000.51-2016《软件产品质量要求和测试细则》是申请软件检测CNAS认可一定会用到的一部国家标准。在前面的文章中,我们为大家整体介绍了GB/T 25000.51-2016《软件产品质量要求和测试细则》国家标准的结构和所涵盖的内容以及对软件产品的八大质量特性中的功能性…...
)
408复试day2(7大排序算法)
数据结构 7大排序算法总结: 首先排序分为内排序和外排序: 内排序是指待排序的记录放置在内存,而外排序是指排序的过程中需要对内存进行访问。其中稳定的排序有“插冒归”,即插入排序、冒泡排序、归并排序。 1.冒泡排序 算法原理&a…...
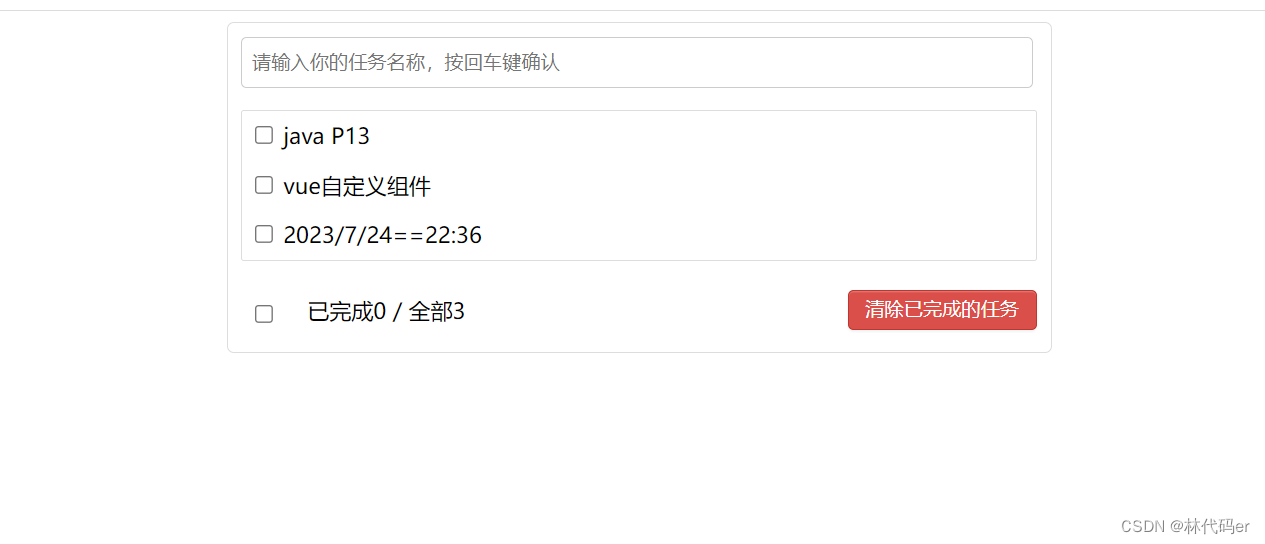
Vue消息订阅与发布
引入第三方库pubsub.js: npm i pubsub-js Student.vue import pubsub from pubsub-jsmethods:{sendStudentName(){// this.$bus.$emit(hello,this.name)pubsub.publish(hello,666)}}, School.vue import pubsub from pubsub-jsmounted() {// console.log("school&quo…...

MySQL学习笔记 ------ 分组查询
#进阶5:分组查询 /* 语法: select 分组函数,列(要求出现在group by的后面) from 表 【where 筛选条件】 group by 分组的列表 【order by 排序的字段】; 注意:查询列表必须特殊,要求是分组函…...

Matlab 点云平面特征提取
文章目录 一、简介二、实现代码2.1基于k个邻近点2.2基于邻近半径参考资料一、简介 点云中存在这各种各样的几何特征,这里基于每个点的邻域协方差来获取该点的所具有的基础几何特征(如下图所示),这样的做法虽然不能很好的提取出点云中的各个部分,但却是可以作为一种数据预处…...
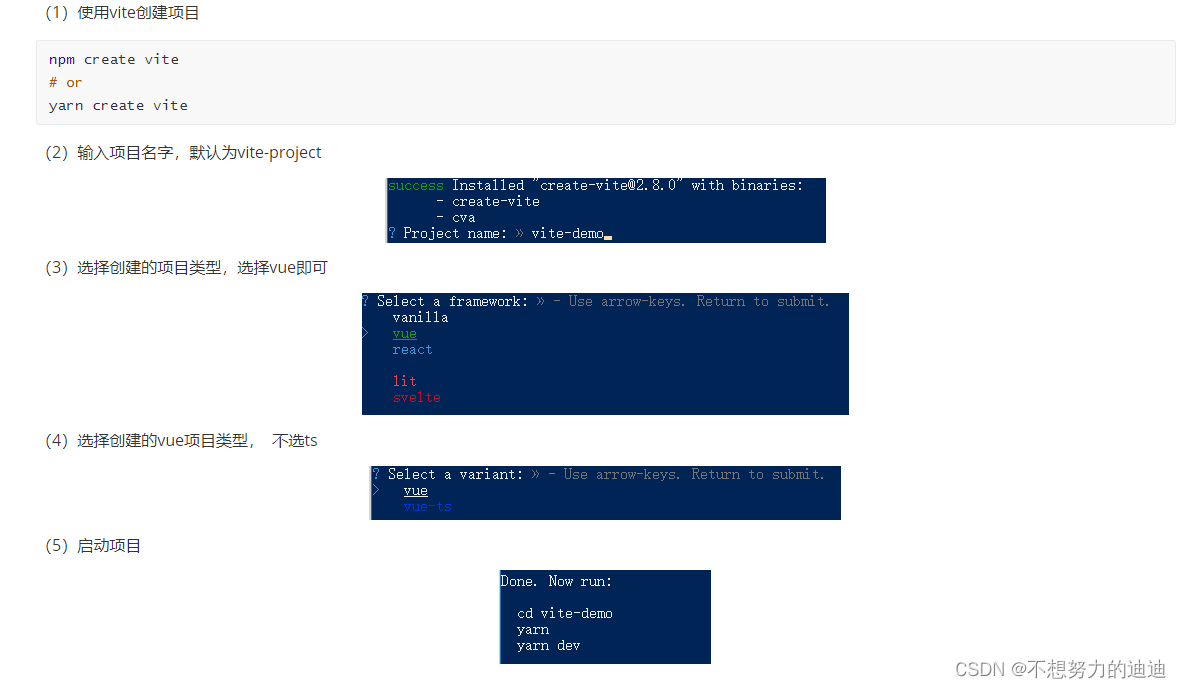
vite的介绍
Vite(法语意为 "快速的",发音 /vit/,发音同 "veet")是一种新型前端构建工具 优势 💡 极速的服务启动,使用原生 ESM 文件,无需打包 ⚡️ 轻量快速的热重载,始终极快的模块…...

裁员 10%,暴跌 14%,这家 IT 独角兽正在被抛弃!
流量一跌再跌,Stack Overflow 简直被狠狠地上了一课! 3 月份 Stack Overflow 的流量下降了近 14%。该公司的 CEO 压力空前,甚至昨天决定裁员 10%! 平均每月下降6%,上月直接跌了近14% 开发人员越来越多地从 AI 聊天机器…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
