《脱离“一支笔、一双手、一道力扣”困境的秘诀》:突破LeetCode难题的五个关键步骤

导言: 在解决LeetCode等编程题时,不少人会陷入“一支笔、一双手、一道力扣(LeetCode)做一宿”的困境。尽管已经掌握了相关知识和算法,但在实际挑战中却无从下手。本文将分享如何摆脱这一困境的秘诀,让你在面对LeetCode难题时能够游刃有余。
第一步:理解问题和限制条件 在开始解决任何问题之前,首先要仔细阅读题目,确保对问题的理解与要求一致。了解问题的限制条件对解决方案的设计和实现也至关重要。在分析问题时,可以绘制示意图或做一些简单的示例分析,帮助自己更好地理解问题。
第二步:找出问题的解决方案 LeetCode题库中的问题涵盖了许多不同类型的算法和数据结构。在解决问题之前,需要确定问题所属的类型,并了解常见的解决方案。可以借助书籍、网上教程或其他资源来学习和掌握相关算法和数据结构。了解解决方案的优劣势,并能灵活选择和应用它们。
第三步:编写伪代码 在开始编写实际代码之前,可以先编写一份伪代码。伪代码是一种简化的代码表示形式,它帮助你将解决方案转化为更具体和可执行的步骤。编写伪代码时,可以使用自然语言或编程语言的部分语法,但不需要太过于细致和精确。伪代码有助于整理思路,确保解决方案的合理性。
第四步:实现代码 通过前面的准备工作,我们现在可以着手实现真正的代码了。在编写代码时,可以按照伪代码的步骤来进行,逐步实现解决方案。尽量保持代码的简洁和可读性,注重命名规范和代码风格。如果遇到bug或问题,可以通过调试和测试来找出原因,并及时进行修复。
第五步:测试和优化 完成代码实现后,需要进行充分的测试来验证解决方案的正确性。可以使用LeetCode的测试用例,或者自行设计一些边界条件的测试数据。通过测试,找出可能存在的问题和潜在的性能瓶颈,并进行优化。优化可以包括算法的改进、数据结构的优化或代码的重构等方面。
总结: 在解决LeetCode难题时,脱离“一支笔、一双手、一道力扣”的困境,需要经过以下关键步骤:理解问题和限制条件、找出解决方案、编写伪代码、实现代码,最后进行测试和优化。这些步骤有助于整理思路、提高解题效率,并更好地应对各种编程挑战。
希望本文的经验和建议能够帮助到你,让你在解决LeetCode难题时更加从容和有效。相信只要你坚持学习和实践,不断积累经验,就能够逐渐脱离困境,成为一个优秀的程序员。加油!
相关文章:

《脱离“一支笔、一双手、一道力扣”困境的秘诀》:突破LeetCode难题的五个关键步骤
导言: 在解决LeetCode等编程题时,不少人会陷入“一支笔、一双手、一道力扣(LeetCode)做一宿”的困境。尽管已经掌握了相关知识和算法,但在实际挑战中却无从下手。本文将分享如何摆脱这一困境的秘诀,让你在面…...
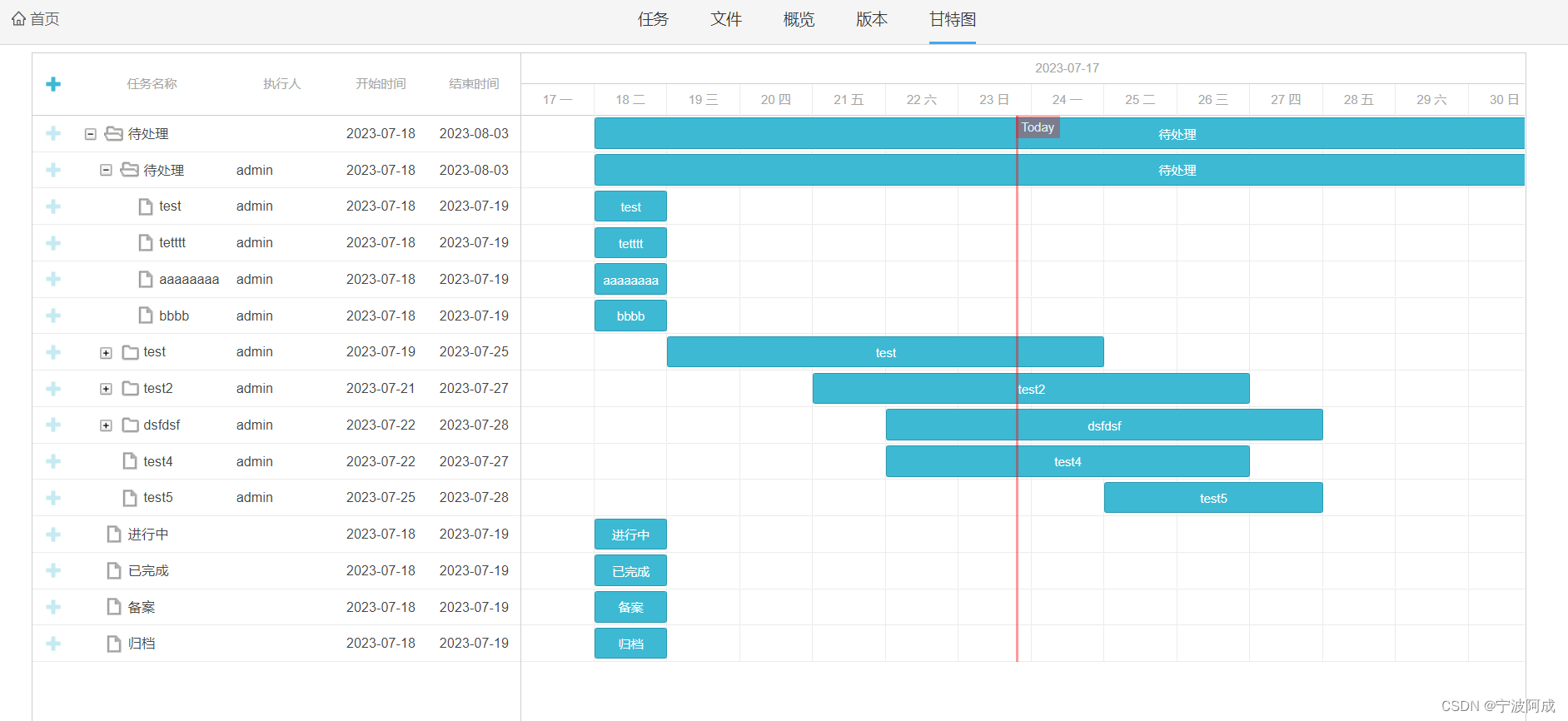
基于jeecg-boot的任务甘特图显示
更多功能看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/nbcio-boot 前端代码:https://gitee.com/nbacheng/nbcio-vue.git 在线演示(包括H5) : http://122.227.135.243:9888 基于项目的任务显…...

docker export,import后无法运行,如java命令找不到,运行后容器内编码有问题
为什么用docker export呢,😔~由于客户环境太恶心了,测试一次更是麻烦,所以什么都得在本地调试完成,争取每次测试上线一次通过才行,说多了都是泪。 由于踩坑几次了,每次都忘记,且每次…...
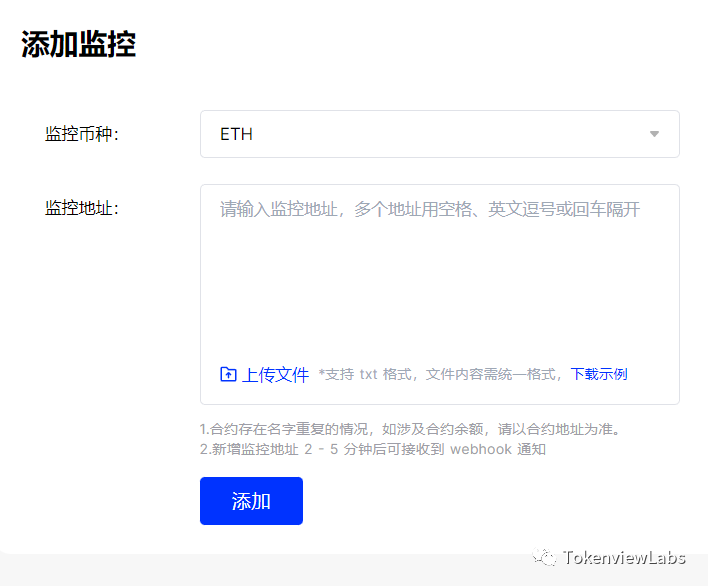
Web3教程| 什么是地址监控?如何使用地址监控追踪黑客地址?
在当今Web3世界里,保护个人资产安全至关重要。据报道在2023年上半年,Web3领域因黑客攻击事件造成的损失高达4.794亿美元。 此外,10多个公链遭受黑客攻击,其中以太坊链遭受的损失最多,约为2.87亿美元。这些黑客的存在迫…...
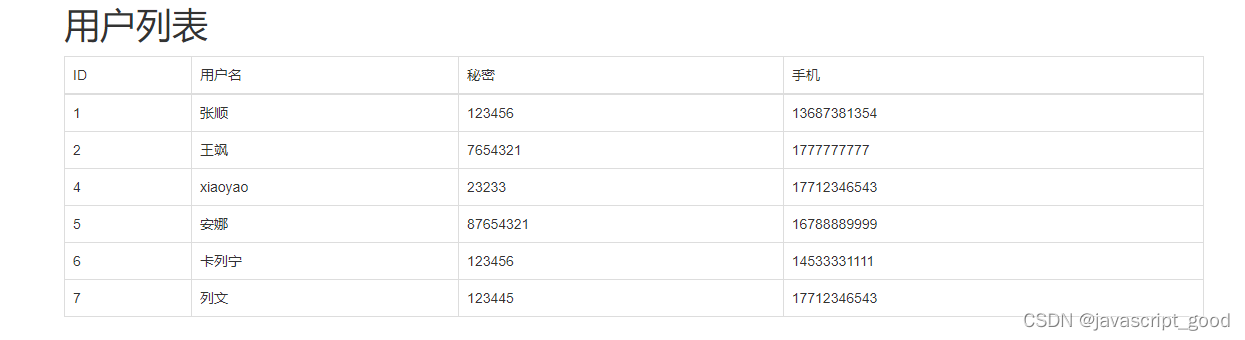
flask结合mysql实现用户的添加和获取
1、数据库准备 已经安装好数据库,并且创建数据库和表 create database unicom DEFAULT CHARSET utf8 COLLATE utf8_general_ci; CREATE TABLE admin( id int not null auto_increment primary key, username VARCHAR(16) not null, password VARCHAR(64) not null…...
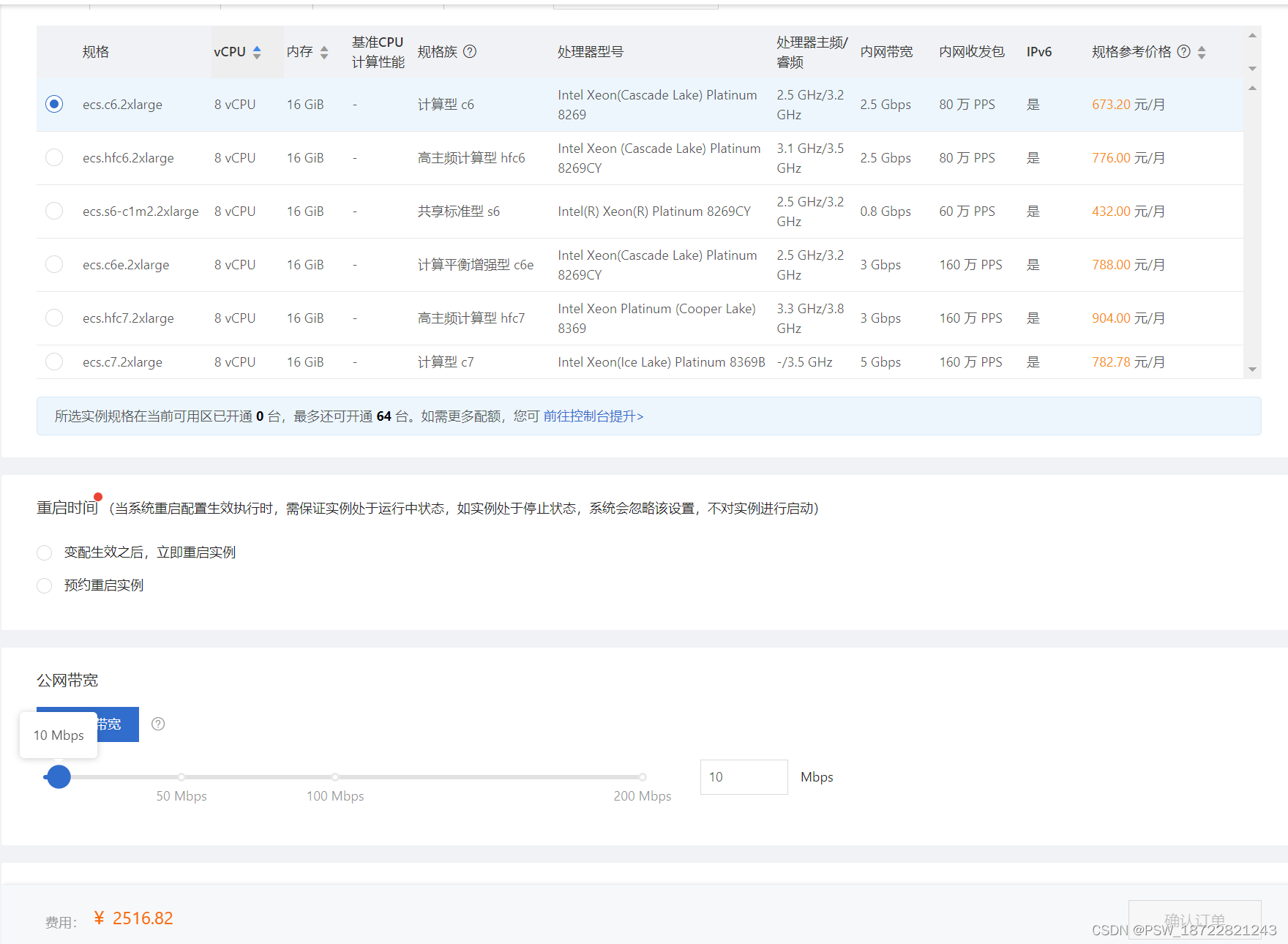
阿里云服务器配置 内存,cpu等等
实例升配,https://help.aliyun.com/document_detail/25438.html?spma2c4g.11174283.6.780.2cbf4c070oeino#title-a5t-gg2-...

PHP注册、登陆、6套主页-带Thinkphp目录解析-【强撸项目】
强撸项目系列总目录在000集 PHP要怎么学–【思维导图知识范围】 文章目录 本系列校训本项目使用技术 上效果图主页注册,登陆 phpStudy 设置导数据库项目目录如图:代码部分:控制器前台的首页 其它配套页面展示直接给第二套方案的页面吧第三套…...

android Activity设置背景为半透明的时候会显示上一个activity的内容
在弹出PopupWindow时将当前Activity设置成了半透明: WindowManager.LayoutParams lp = this.activity.getWindow().getAttributes();lp.alpha = 0.5f; //0.0-1.0this...
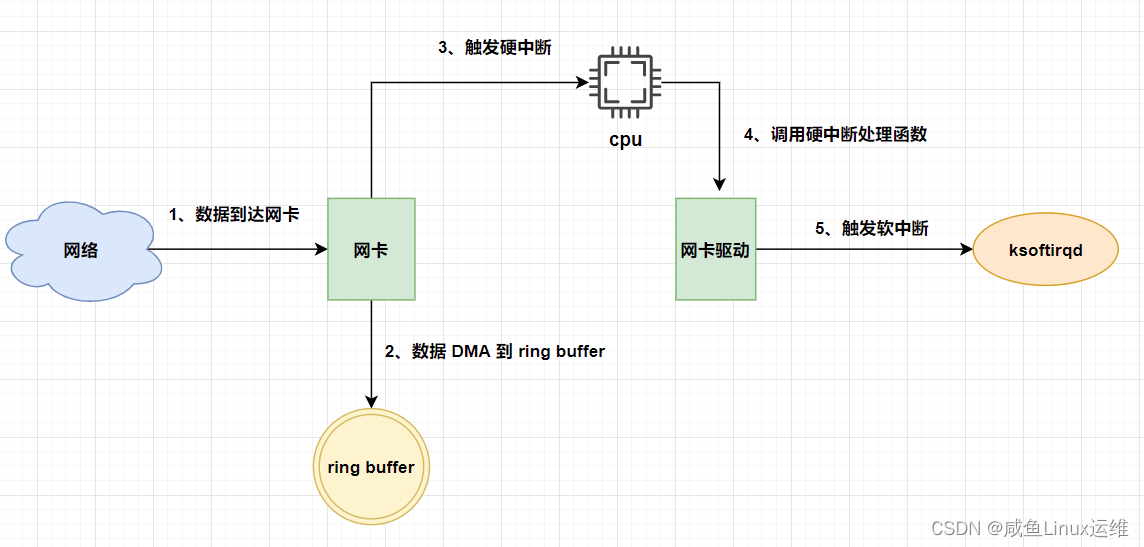
Linux 网络收包流程
哈喽大家好,我是咸鱼 我们在跟别人网上聊天的时候,有没有想过你发送的信息是怎么传到对方的电脑上的 又或者我们在上网冲浪的时候,有没有想过 HTML 页面是怎么显示在我们的电脑屏幕上的 无论是我们跟别人聊天还是上网冲浪,其实…...

flex: 0 0 273px的意思
flex: 0 0 273px; 是一条CSS属性,用于设置flexible box布局(flexbox)中的flex子项的灵活性和尺寸。 这条属性包含三个值,分别是: flex-grow: 表示弹性增长因子,指定当有多余空间时,子项能够增长…...
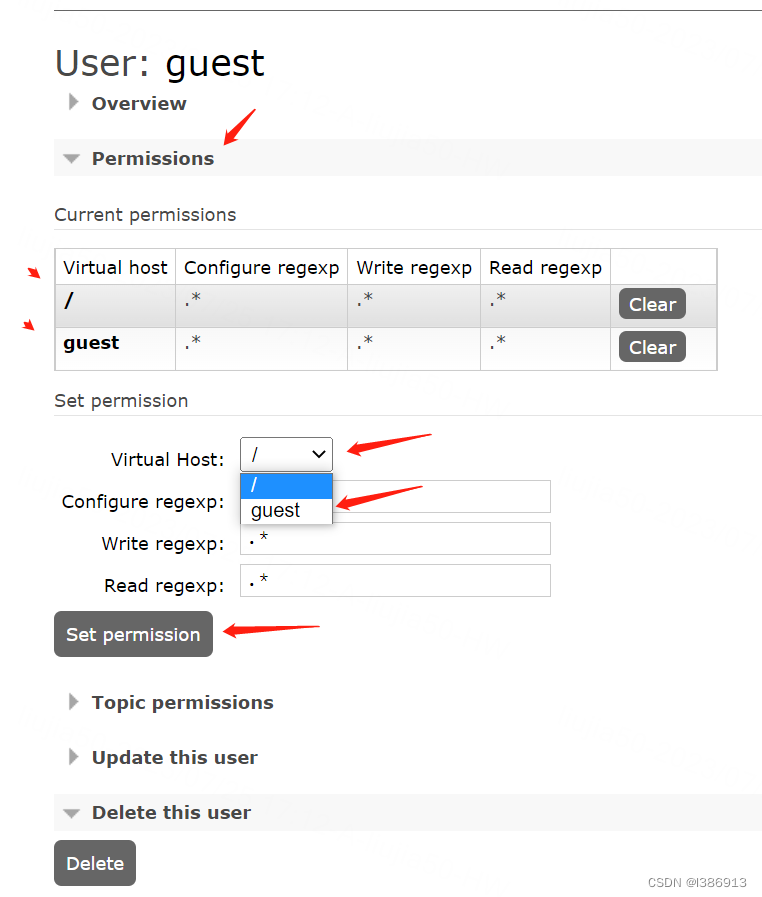
helm部署rabbitmq
1.添加rabbitmq仓库并下载包 helm repo add bitnami https://charts.bitnami.com/bitnami helm pull bitnami/rabbitmq --version 10.1.4 tar -zxvf rabbitmq-10.1.4.tgz mv values.yaml values.yaml.back grep -v "#" values.yaml.back > values.yaml2.helm部署…...
Java版Spring Cloud+Spring Boot+Mybatis+uniapp知识付费平台讲解
提供私有化部署,免费售后,专业技术指导,支持PC、APP、H5、小程序多终端同步,支持二次开发定制,源码交付。 Java版知识付费-轻松拥有知识付费平台 多种直播形式,全面满足直播场景需求 公开课、小班课、独…...

编程之舞:流程控制乐章
流程控制语句 1. 复合语句 2. 条件语句2.1 if条件语句2.2 switch多分支语句 3. 循环语句3.1 while循环语句3.2 do...while循环语句3.3 for循环语句 4. 循环控制4.1 break语句4.2 continue语句 5. 实践与练习 1. 复合语句 复合语句是由一对花括号括起来的语句块,可以…...

ChatGPT是否能够进行情感融合和语气调整?
ChatGPT是一种预训练的通用语言模型,具有很强的文本生成和理解能力。在情感融合和语气调整方面,ChatGPT可以通过特定的技术和训练方法实现一定程度的情感表达和语气调整。下面将详细探讨ChatGPT在情感融合和语气调整方面的应用方法和潜力。 1. **情感融…...

C++--动态规划路径问题
1.不同路径 力扣 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从…...
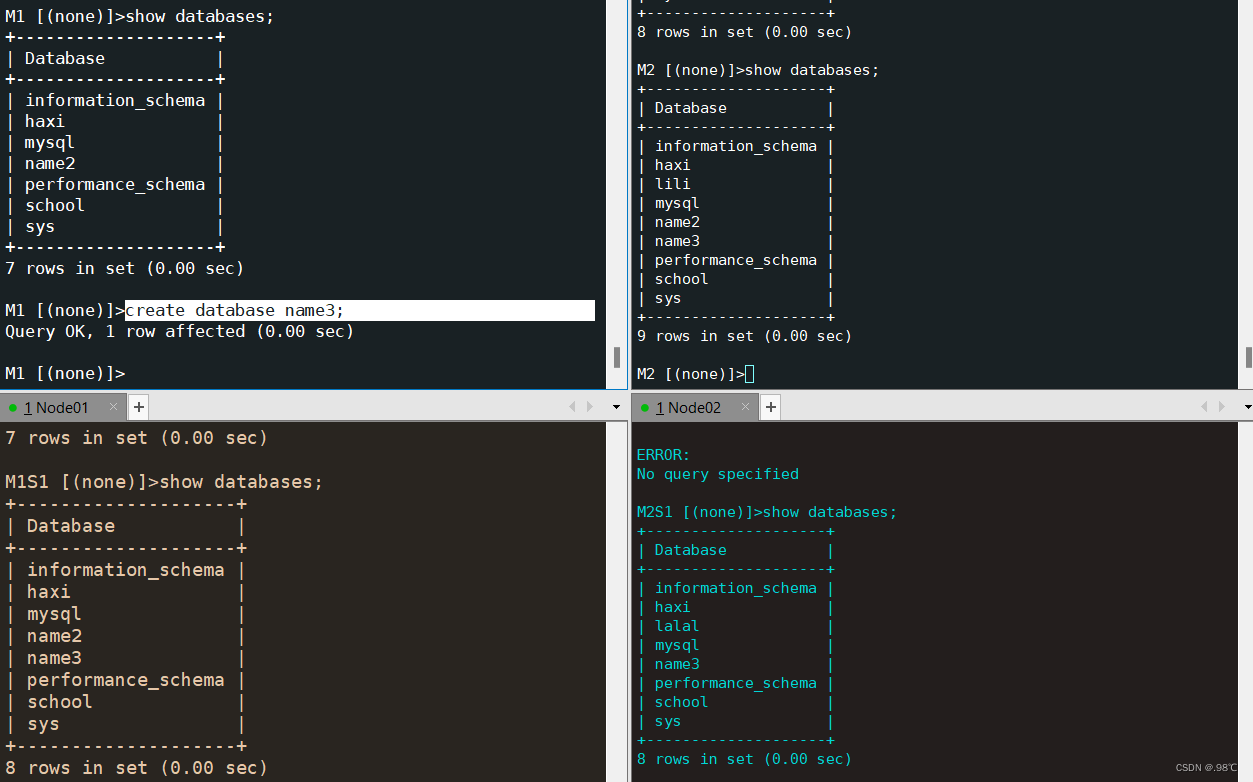
从实践彻底掌握MySQL的主从复制
目录 一、本次所用结构如图---一主多从级联: 二、IP。 三、配置M1: 四、从库M1S1: 五、从库M2配置: 六、 从库M2S1: 一、本次所用结构如图--- 一主多从级联: 二、IP。这里M1S1和M1S2一样的࿰…...

机器学习深度学习——线性回归的基本元素
回归用来表示输入输出之间的关系。 用实际例子来解释一下线性回归:根据房屋的面积、房龄来估算房屋价格。为了实现这个预测放假的模型,需要收集一个真实的数据集,该数据集包括了房屋的销售价格、面积和房龄。 在机器学习中,这个数…...
K8S初级入门系列之八-网络
一、前言 本章节我们将了解K8S的相关网络概念,包括K8S的网络通讯原理,以及Service以及相关的概念,包括Endpoint,EndpointSlice,Headless service,Ingress等。 二、网络通讯原理和实现 同一K8S集群&…...

分段@Transactional 坑及失效问题
Transactional 背景:在某些情况下,我们需要分段transaction,在最外面没有transaction,里面分成几个transaction,保证分段是成功的。 问题代码: Service public Order getOrder1(String id) {Optional<Or…...
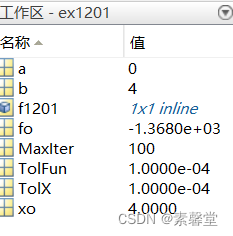
25、matlab里面的10中优化方法介绍——Opt_Golden法(matlab程序)
1.简述 基本思想 黄金分割法也称为 0.618 法,其基本思想是通过取试探点和进行函数值比较,使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。 公式推导 设有定义在[ a , b ] [a,b][a,b]上的单谷函数 φ ( …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
