Java 贪心算法经典问题解决
文章目录
- 分金条
- 题目
- 思路
- 代码实现
- 测试用例以及结果输出
- 花费资金做项目最大收益
- 题目
- 思路
- 代码实现
- 测试用例以及结果输出
- 预定会议室
- 题目
- 思路
- 代码实现
- 测试用例以及结果输出
- 取中位数
- 题目
- 思路
- 代码实现
- 测试用例以及结果输出
- 最低字典序
- 题目
- 思路
- 代码实现
- 测试用例以及结果输出
- 结语
分金条
题目
一块金条切成两半,是需要花费和长度数值一样的铜板的。比如 长度为20的 金条,不管切成长度多大的两半,都要花费20个铜 板。一群人想整分整块金 条,怎么分最省铜板?
例如,给定数组{10,20,30},代表一共三个人,整块金条长度为 10+20+30=60. 金条要分成10,20,30三个部分。 如果, 先把长 度60的金条分成10和50,花费60 再把长度50的金条分成20和30, 花费50 一共花费110铜板。 但是如果, 先把长度60的金条分成30和30,花费60 再把长度30 金条分成10和20,花费30 一共花费90铜板。
输入一个数组,返回分割的最小代价。
思路
哈夫曼树带权路径计算问题,更多了解可参考:哈夫曼树及其应用
- 先将给定数组进行排序,这里可以使用优先级队列处理【优先级堆结构】,将数组依次丢入优先级队列中;
- 每次从优先级队列中取出较小的值相加,记录计算结果,同时将结果重新丢入到队列中,直到队列中没有元素;
- 将过程中的所有计算结果相加,结果即为分割最小代价;
代码实现
private static int lessMoney(int[] aar) {PriorityQueue<Integer> pQ = new PriorityQueue<>();for (int i = 0; i < aar.length; i++) {pQ.add(aar[i]);}int result = 0;int cur = 0;while (pQ.size() > 1) {cur = pQ.poll() + pQ.poll();result += cur;pQ.add(result);}return result;}
测试用例以及结果输出
public static void main(String[] args) {int[] aar = new int[]{30, 10, 20};System.out.println(lessMoney(aar));}
输出结果:
90
花费资金做项目最大收益
题目
输入:
参数1,正数数组costs
参数2,正数数组profits
参数3, 正数k
参数4,正数m
其中,costs[i]表示i号项目的花费;profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润);
k表示你不能并行、只能串行的最多做k个项目;
m表示你初始的资金;
说明:你每做完一个项目,马上获得的收益,可以支持你去做下一个 项目。
输出:你最后获得的最大钱数。
思路
基本原则:结合生活中的实际生产,每次选花费最小收益最高的项目去做,最终得到的收益肯定是最大的;
- 新定义Node类,包含每个项目对应的花费以及收益;
- 分别定义两个优先级队列,按照最小花费和最大收益优先级取元素;
- 将根据花费以及收益数组生成的Node数组丢入到最小花费优先级队列中;
- 进行K次遍历【最多可以做K个项目】,不断从最小花费优先级队列中取出项目,丢入到最大收益优先级队列中【注意资金问题】,在根据最大收益去做项目【即从最大收益队列中取项目做】,计算过程中获取的收益之和;
代码实现
/*** 计算最大收益** @param k 表示能做K个项目* @param m 表示启动资金* @param profits 表示做每个项目去除花费后的利润* @param costs 表示做每个项目对应的花费* @return*/private static int getMaxProfit(int k, int m, int[] profits, int[] costs) {//将项目对应花费以及收益包装成Node类,添加到Node[]数组中Node[] nodes = new Node[costs.length];for (int i = 0; i < costs.length; i++) {nodes[i] = new Node(costs[i], profits[i]);}// 最小花费优先级队列PriorityQueue<Node> minConstQ = new PriorityQueue<>(new MinComparator());// 最大收益优先级队列PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxComparator());//添加到最小花费优先级队列中for (int i = 0; i < nodes.length; i++) {minConstQ.add(nodes[i]);}// k表示最多可以做k个项目for (int i = 0; i < k; i++) {//只要花费不超过启动资金,按照最小花费不断从队列中取,丢入到收益队列中while (!minConstQ.isEmpty() && minConstQ.peek().cost <= m) {maxProfitQ.add(minConstQ.poll());}//如果收益队列为空,就返回最终资金,否则每次从收益队列中取最大收益的项目去做;if (maxProfitQ.isEmpty()) {return m;}m = m + maxProfitQ.poll().profit;}return m;}private static class Node {/*** 花费*/public int cost;/*** 利润*/public int profit;public Node(int cost, int profit) {this.cost = cost;this.profit = profit;}}/*** 花费最小排序*/private static class MinComparator implements Comparator<Node> {@Overridepublic int compare(Node o1, Node o2) {return o1.cost - o2.cost; //>0表示o1>o2}}/*** 利润最大排序*/private static class MaxComparator implements Comparator<Node> {@Overridepublic int compare(Node o1, Node o2) {return o2.profit - o1.profit; // >0 表示o2>o1}}
测试用例以及结果输出
public static void main(String[] args) {int k = 3;int m = 5;int[] profits = new int[]{1, 3, 4, 6, 8};int[] costs = new int[]{3, 6, 4, 2, 6};System.out.println(getMaxProfit(k, m, profits, costs));}输出结果:
23
预定会议室
题目
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。
给你每一个项目开始的时间和结束的时间(给你一个数组,里面是一个个具体的项目),你来安排宣讲的日程,
要求会议室进行的宣讲的场次最多,返回这个最多的宣讲场次。
思路
优先做最早结束的项目,保证开始时间小于或等于要做项目的开始时间即可;
代码实现
private static int getMaxProgram(Program[] program, int start) {Arrays.sort(program, new ProgramComparator());int result = 0;for (int i = 0; i < program.length; i++) {if (start <= program[i].start) {result++;start = program[i].end;}}return result;}/*** 定义项目会议 包含开始和结束时间*/private static class Program {public int start;public int end;public Program(int start, int end) {this.start = start;this.end = end;}}/*** 按哪个项目先结束排序*/private static class ProgramComparator implements Comparator<Program> {@Overridepublic int compare(Program o1, Program o2) {return o1.end - o2.end;}}
测试用例以及结果输出
public static void main(String[] args) {Program p1 = new Program(6, 10);Program p2 = new Program(7, 8);Program p3 = new Program(11, 13);Program p4 = new Program(13, 15);Program[] programs = new Program[]{p1, p2, p3, p4};System.out.println(getMaxProgram(programs, 6));}
输出结果:
3
取中位数
题目
一个数据流中,随时可以取得中位数;
思路
分别定义大根堆和小根堆,以下述逻辑进行存放和调整;
- 当大根堆为空时,元素直接添加到大根堆中;
- 当大根堆不为空时,如果元素小于或等于大根堆堆顶元素,则添加到大根堆中,否则添加到小根堆中;
- 当大根堆和小根堆元素个数相差为2时,需要进行堆调整,将元素个数多的堆堆顶元素放入元素个数少的堆中;
- 计算中位数,当大根堆和小根堆元素个数相等,则中位数为取两个堆的堆顶元素之和除以2,如果元素个数不相等,则中位数为元素个数多的堆的堆顶元素;
下面以以图进行举例说明,这里简单以队列表示大小根堆:
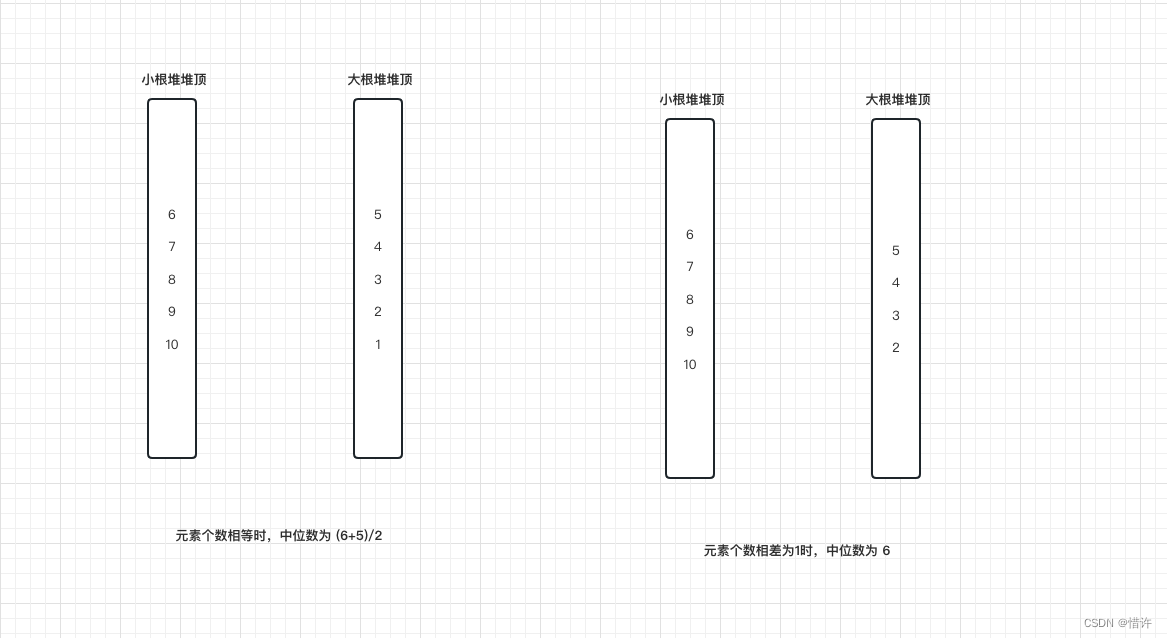
可以理解成通过堆对元素进行排序,只不过利用大小根队的性质,保证中位数可以通过堆顶数据进行计算得出,也避免了每次添加元素时进行排序问题,时间复杂度更低;
代码实现
private static class MedianHelper {private PriorityQueue<Integer> minQ = new PriorityQueue<>(new MinComparator());private PriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxComparator());public int getMedian() {int maxQSize = maxQ.size();int minQSize = minQ.size();if (maxQSize == 0) {return 0;}//元素个数相等,取两者堆顶元素/2if (maxQSize == minQSize) {return (maxQ.peek() + minQ.peek()) / 2;}//元素个数不相等,取元素多的堆顶元素return maxQSize > minQSize ? maxQ.peek() : minQ.peek();}//插入元素public void addNum(int num) {if (maxQ.isEmpty()) {maxQ.add(num);} else {if (maxQ.peek() >= num) {maxQ.add(num);} else {minQ.add(num);}}modifyQSize();}/*** 调整两个堆的大小 一旦发现两个堆数据个数相差为2,则取多的丢到少的里面*/private void modifyQSize() {int minQSize = minQ.size();int maxQSize = maxQ.size();if (minQSize - maxQSize == 2) {maxQ.add(minQ.poll());}if (maxQSize - minQSize == 2) {minQ.add(maxQ.poll());}}}
测试用例以及结果输出
public static void main(String[] args) {int[] aar = new int[]{8, 6, 13, 10, 11, 19};MedianHelper helper = new MedianHelper();for (int i : aar) {helper.addNum(i);}System.out.println(helper.getMedian());}
输出结果:
10
最低字典序
题目
给定一个字符串类型的数组strs,找到一种拼接方式,使得把所有字符串拼起来之后形成的字符串具有最低的字典序。
思路
保证每次拼接后的字符串都是最低字典序的即可;
代码实现
private static String lowestString(String[] strs) {if (strs == null || strs.length == 0) {return "";}Arrays.sort(strs, new LowestComparator());StringBuilder result = new StringBuilder();for (int i = 0; i < strs.length; i++) {result.append(strs[i]);}return result.toString();}/*** 定义两个字符拼接最小字典序比较器*/private static class LowestComparator implements Comparator<String> {@Overridepublic int compare(String o1, String o2) {return (o1 + o2).compareTo(o2 + o1);}}
测试用例以及结果输出
public static void main(String[] args) {String[] strs2 = {"b", "ab", "ac"};System.out.println(lowestString(strs2));}
结果输出:
abacb
结语
如果以上文章对您有一点点帮助,希望您不要吝啬的点个赞加个关注,您每一次小小的举动都是我坚持写作的不懈动力!ღ( ´・ᴗ・` )
相关文章:

Java 贪心算法经典问题解决
文章目录 分金条题目思路代码实现测试用例以及结果输出 花费资金做项目最大收益题目思路代码实现测试用例以及结果输出 预定会议室题目思路代码实现测试用例以及结果输出 取中位数题目思路代码实现测试用例以及结果输出 最低字典序题目思路代码实现测试用例以及结果输出 结语 分…...
所有docker命令无效,解决办法
目录 ■前言 今天使用docker时,所有命令无效 ■解决办法如下 1.停止docker服务 2.查看状态 3.删除之前的docker相关的文件 4.再次查看状态 5.使用相关命令 (好用了) 6.重新下载镜像 ■前言 今天使用docker时,所有命令无…...

系列一、创建者模式
一、概述 创建者模式的主要关注点是"怎样创建对象?",它的主要特点是"将对象的创建与使用分离"。这样可以降低系统的耦合度,使用者不需要关注对象的创建细节。 二、分类 单例模式工厂方法模式抽象工厂模式原型模式建造者模式...
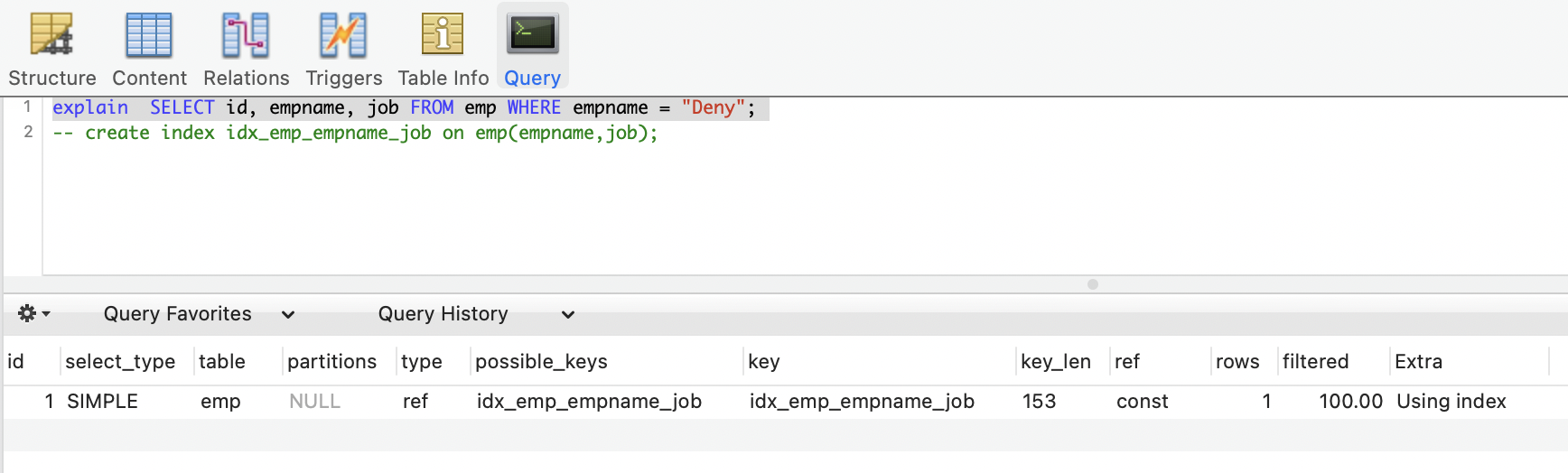
数据库系列:覆盖索引和规避回表
1 介绍 在MySQL数据库查询过程中,索引覆盖和避免不必要的回表,是减少检索步骤,提高执行效率的有效手段。下面从这两个角度分析如何进行MySQL检索提效。 2 数据准备 模拟一个500w数据容量的部门表 emp,表结构如下,并…...
java Spring Boot上线运维 启动jar时控制台调整零时变量
前面的文章 java 打包Spring Boot项目,并运行在windows系统中和将Spring Boot项目打包部署到阿里云linux服务器讲述了Spring Boot项目打包部署的过程 但是 这里 我们可能会遇到一种情况 此时 我们服务器 java项目占用了 80端口 但我们需要放上去一个更重要的东西&am…...

java后端校验
Java 后端数据校验 一、概述 当我们想提供可靠的 API 接口,对参数的校验,以保证最终数据入库的正确性,是 必不可少 的活。比如下图就是 我们一个项目里 新增一个菜单校验 参数的函数,写了一大堆的 if else 进行校验,…...
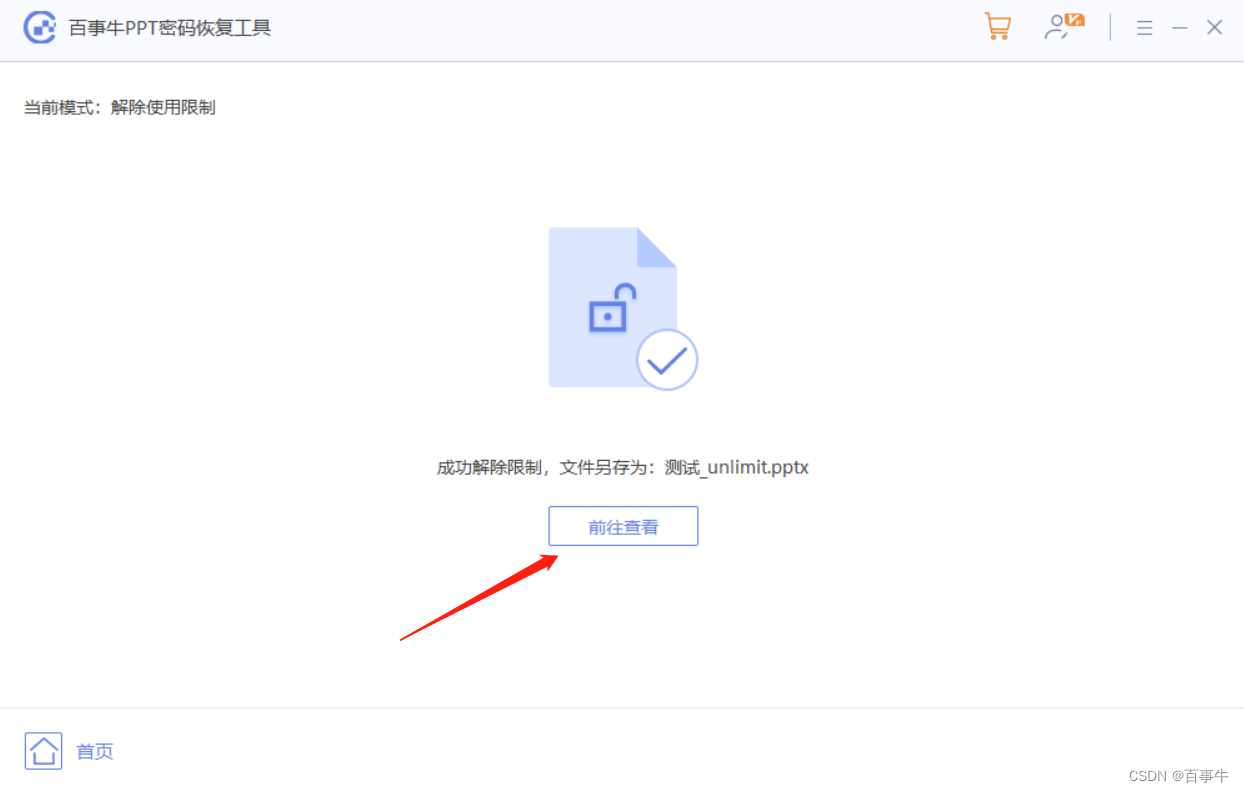
PowerPoint如何修改“默认保存路径”?
很多时候,我们做好PPT后都要保存,一般会保存在创建PPT的文件夹里,或者另外设置保存的路径。 如果经常需要制作PPT,又不想每次都要重新选择保存位置,我们可以创建或修改“默认保存路径”,这样每次关闭PPT后…...

【PMP】有没有项目经理能看得懂这九张图?求挑战
这九张图,全是圈圈我的肺腑之言啊!谁痛谁知道! 做技术时,就想着30岁就转管理,管理岗位赚得多,结果发现全是烟雾弹。 做技术和代码打交道,做管理跟人打交道。天天开不完的会、说不完的话…...

ES6学习记录—自己记录一直更新版
1. 什么是ECMA 全称:European computer manufacturers association欧洲计算机制造联合会; 2、它的标准名单中的:ECMA — 262脚本语言的规范:规范化脚本语言,叫ECMAScript ( 一定要记住);像ES5 ES6就是这样来的…...

linux操作gpio的一些记录
在linux里面使用GPIO的一些知识点记录如下: 一、驱动里面操作GPIO 在linux内核里面如果 pinctrl 子系统将一个 PIN 复用为 GPIO 的话,那么就可以用gpio 子系统提供的 API 函数操做gpio,比如设置 GPIO为输入输出,读取 GPIO 的值等…...

目前新能源汽车充电桩的发展受到哪些不利因素的影响?
目前新能源汽车充电桩的发展受到哪些不利因素的影响? 一是安装难,很多老旧小区没有充电桩配套施工规范,充电桩建设比较难,受到充电容量不足电表箱供电等局限性的制约,同时缺乏充电桩配套设施的统一规划,小区内只能安装…...
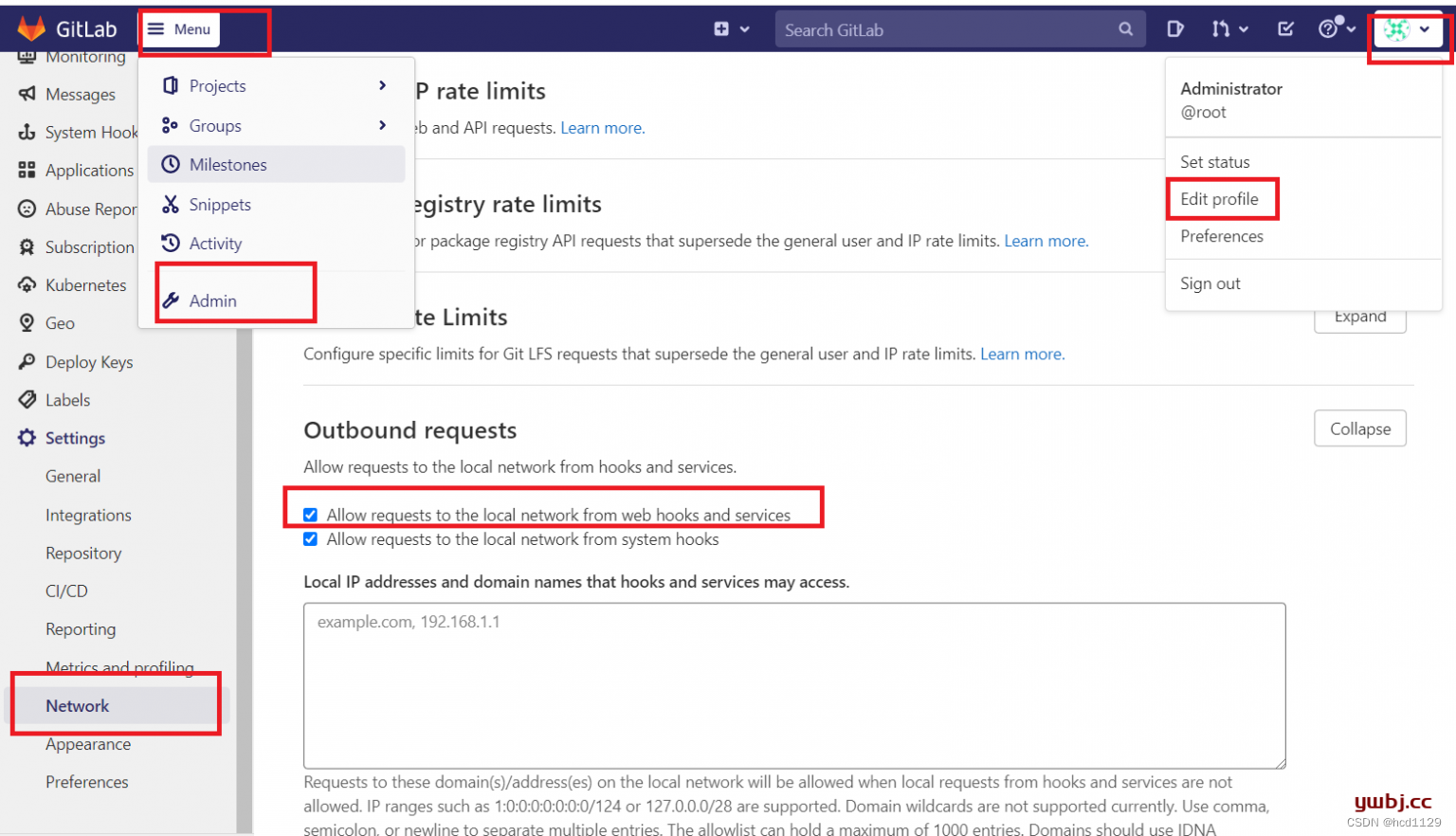
jenkins
Gitlab添加钩子 测试钩子 添加完成后,下面会出现钩子选择。点击test中的,push event。 出现successful,既添加成功。 如果添加失败,报错,更改Network...

基于深度学习的图像分割技术探究
导言: 图像分割是计算机视觉领域的重要任务,旨在将图像划分为不同的语义区域,实现对图像中感兴趣物体的定位和提取。深度学习作为图像分割的新兴技术,通过卷积神经网络(CNN)等模型,取得了显著的…...

【c++】vector的使用与模拟实现
🚀write in front🚀 📜所属专栏:初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对…...

记录安装stable diffusion webui时,出现的gfpgan安装卡住的问题
参考链接:(145条消息) 使用stable diffusion webui时,安装gfpgan失败的解决方案(windows下的操作)_新时代原始人的博客-CSDN博客...
【开发环境】Windows下搭建TVM编译器
关于搭建TVM编译器的官方文档:Install from Source — tvm 0.14.dev0 documentation (apache.org) 1. 安装Anaconda 首先我们需要安装Anaconda,因为其中包含着我们所需要的各类依赖: 进入Anaconda官网https://www.anaconda.com/products/d…...
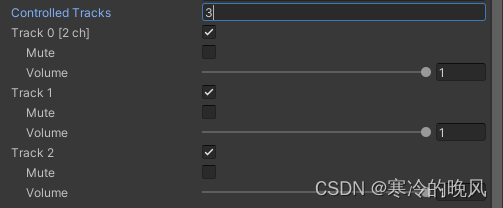
了解Unity编辑器之组件篇Video(二)
Video Player组件:用于在游戏中播放视频的组件。它提供了一系列属性来控制视频的播放、显示和交互。 1.Source(视频源):用于指定视频的来源。可以选择两种不同的视频源类型: (1)Vieo Clip&#…...

安全杂记 - 状态码,DNS,编码
目录 1.状态码2.DNS解析过程3.URL编码4.HTML实体编码5.FORM表单 1.状态码 200 - 请求成功 301 - 资源(网页等)被永久转移到其它URL 302 - 临时移动。与301类似。但资源只是临时被移动。客户端应继续使用原有URI 304 - 未修改。所请求的资源未修改&#…...
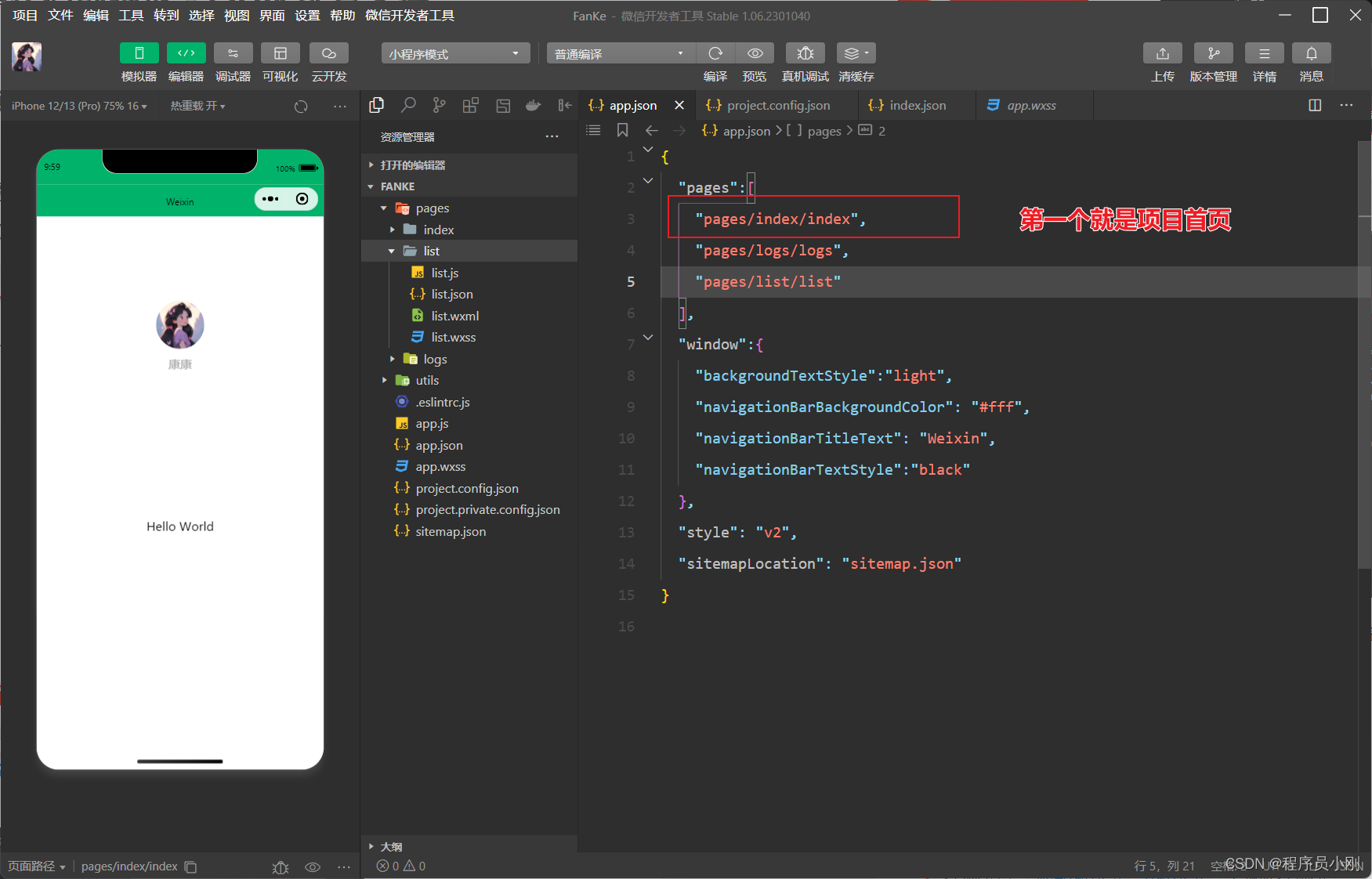
微信小程序 Page页面
新建页面只需要在app.json配置好路径,编译器自动新增了页面 项目首页,在app.json哪个页面是第一位,哪个页面就是小程序首页...

C语言实现基于Linux,epoll和多线程的WebServer服务器
代码结构: Server.h 头文件,对函数进行了声明 #pragma once #include<stdio.h> // 新建一个用于TCP监听的socket文件描述符,并返回 int initListenFd(unsigned short port);// 启动epoll int epollRun(int lfd);// accept建立连接 vo…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
