线性代数(主题篇):第三章:向量组 、第四章:方程组
文章目录
- 第3章 n维向量
- 1.概念
- (1)n维单位列向量
- 2.向量、向量组的的线性关系(线性相关性)
- (1)线性表示 :AX=β
- (2)线性相关、线性无关: AX=0
- ①线性相关
- ②线性无关
- ③线性相关性7大定理
- 3.极大线性无关组、等价向量组、向量组的秩
- 1.极大线性无关组
- 2.等价向量组
- 3.向量组的秩
- 4.向量空间
- (1)向量空间的概念
- (2)基
- (3)基变换的过渡矩阵
- (4)向量在基下的坐标
- 第4章 线性方程组
- (一)具体型线性方程组
- 1.齐次线性方程组 Ax=0
- (1)有解的条件:齐次线性方程组解的判别
- (2)解的性质:齐次解的性质
- 解的叠加性:解的线性组合也是解
- (3)基础解系、通解的结构
- ①基础解系
- ②通解的结构
- ③自由变量
- (4)求解方法和步骤
- 2.非齐次线性方程组 Ax=β
- (1)有解的条件:非齐次线性方程组解的判别
- (2)解的性质:非齐次解的性质
- (3)求解方法和步骤
- (4)非齐次线性方程组的几何意义:3个方程代表3个平面,交点代表解的个数
- (二)抽象型线性方程组
- (三)方程组的公共解、同解方程组
- 1.方程组的公共解
- 2.同解方程组
第3章 n维向量
1.概念
§ 3 §3 §3 向量组 { ①部分相关,整体相关 ②整体无关,部分无关 ③低维无关,高维无关 ④高维相关,低维相关 \begin{cases} ①部分相关,整体相关\\ ②整体无关,部分无关\\ ③低维无关,高维无关\\ ④高维相关,低维相关 \end{cases} ⎩ ⎨ ⎧①部分相关,整体相关②整体无关,部分无关③低维无关,高维无关④高维相关,低维相关
(1)n维单位列向量
α = ( a 1 a 2 a 3 . . . a n ) , α T = ( a 1 , a 2 , a 3 , . . . , a n ) α=\left(\begin{array}{c} a_1 \\ a_2 \\ a_3 \\ ...\\ a_n \end{array}\right),α^T=(a_1,a_2,a_3,...,a_n) α= a1a2a3...an ,αT=(a1,a2,a3,...,an)
性质:若α是n维列向量,则
1.
①一列乘一行,是矩阵: α α T αα^T ααT 是 n × n n×n n×n阶方阵
②一行乘一列,是一个数: α T α = ∣ ∣ α ∣ ∣ 2 α^Tα=||α||^2 αTα=∣∣α∣∣2
2. t r ( α α T ) = α T α tr(αα^T)=α^Tα tr(ααT)=αTα
3. r ( α α T ) = 1 r(αα^T)=1 r(ααT)=1
4. ( α α T ) T = α α T , ∴ α ⋅ α T (αα^T)^T=αα^T,∴α·α^T (ααT)T=ααT,∴α⋅αT是n阶实对称方阵,可以相似对角化,
α ⋅ α T ∼ ( 1 0 . . . 0 ) α·α^T\sim\left(\begin{array}{cc} 1 & & \\ & 0 & \\ & & ...\\ & & & 0 \end{array}\right) α⋅αT∼ 10...0
例题1:17年5.

分析:不可逆,即|A|=λ₁λ₂λ₃…=0,即有0特征值
α α T ∼ ( 1 0 . . . 0 ) αα^T\sim\left(\begin{array}{cc} 1 & & \\ & 0 & \\ & & ...\\ & & & 0 \end{array}\right) ααT∼ 10...0 ,显然 E − α α T E-αα^T E−ααT有零特征值,不可逆
答案:A
2.向量、向量组的的线性关系(线性相关性)
(1)线性表示 :AX=β
若存在常数 k 1 , k 2 , . . . , k s , k_1,k_2,...,k_s, k1,k2,...,ks,使得 α = k 1 β 1 + k 2 β 2 + . . . + k s β s , α = k_1β_1+ k_2β_2+...+ k_sβ_s, α=k1β1+k2β2+...+ksβs,则称向量 α α α是向量组 β 1 , β 2 , . . . , β s β_1,β_2,...,β_s β1,β2,...,βs的线性组合,或称向量 α α α可被向量组 β 1 , β 2 , . . . , β s β_1,β_2,...,β_s β1,β2,...,βs线性表示(线性表出)
哪个向量前面的系数不为0,这个向量就可以被其余向量线性表示
例题1:03年10.
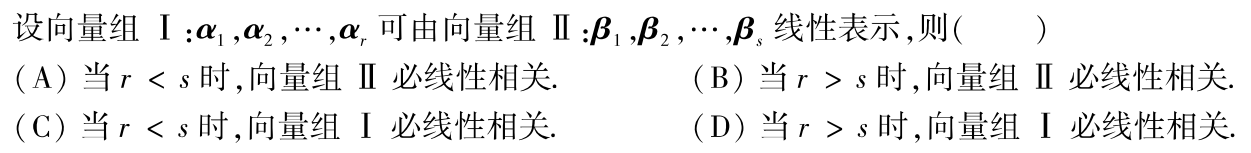
答案:D
例题2:数二 21年9. 线性表示

分析:

答案:D
例题3:20年6. 直线的点向式方程→直线的参数方程→直线参数方程的向量形式 + 线性表示

分析:

答案:C
(2)线性相关、线性无关: AX=0
①线性相关
1.定义:设向量组α1,α2,…,αs,若存在不全为0的数k1,k2,…,ks,使 k 1 α 1 + k 2 α 2 + . . . + k s α s = 0 k_1α_1+k_2α_2+...+k_sα_s=0 k1α1+k2α2+...+ksαs=0,则称向量组α1,α2,…,αs线性相关
2.线性相关的充要条件:α1,α2,…,αs中至少有一个向量可以被其他向量线性表示
线性相关的向量组中,系数不为0的向量,可由其他向量线性表示
3.线性相关的等价条件:
⇦⇨ 至少有一个向量可由其余n-1个向量线性表出

4.通过初等变换,无关 可变 相关,但 已相关 不可回 无关

5.含有零向量或成比例向量的向量组,必线性相关
显然,若向量组中有零向量,则向量组线性相关。(可取零向量α0的系数k0为任意非零常数,破坏了线性无关的定义。)
即含有零向量的向量组线性相关。
本来线性无关的向量组,加入一个零向量,它们就线性相关了。可见零向量就是一个润滑剂
②线性无关
1.定义:设向量组α1,α2,…,αs,若不存在不全为0(仅存在全为0)的数k1,k2,…,ks,使k1α1+k2α2+…+ksαs=0,则称向量组α1,α2,…,αs线性无关
2.推论:设向量组α1,α2,…,αs线性无关,但向量组α1,α2,…,αs,β线性相关。则向量β可由向量组α1,α2,…,αs线性表示,且表示法唯一。
3.线性无关的等价条件:
①行列式|A|≠0
②A可逆
③满秩:r(A)=n
④AX=0仅有零解
⑤向量组不成比例
③线性相关性7大定理
1.线性相关 ⇦⇨ 至少有一个向量可由其余n-1向量线性表出
线性无关 ⇦⇨ 任一向量均不能由其余n-1个向量线性表出


2.原来无关,加一个相关,则新加的可被原向量组 唯一线性表示
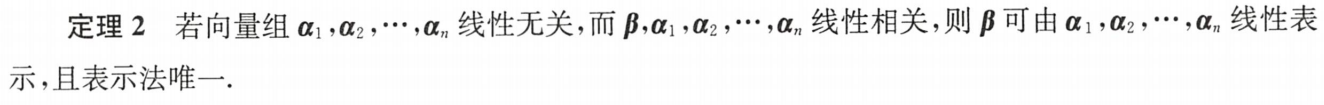
证明:


非0不可由0表示:若向量α第k行非0,其他向量第k行均为0,则α不可由其他向量线性表示
0向量可由非0向量表示:零向量 = 0×非零向量
3.以少表多,多的相关、秩多的可以表示秩少的
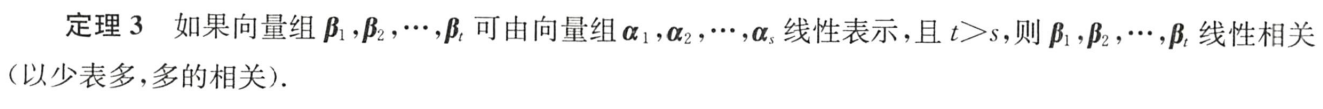
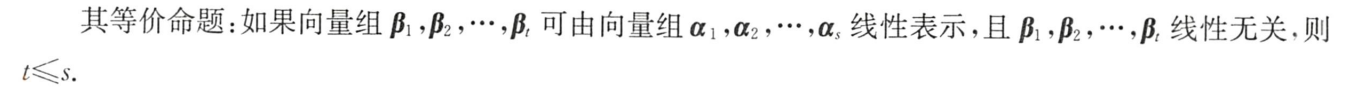
高维空间可表示低维空间,反之不可 【秩多的可以表示秩少的】
4.Ax=0 仅有零解,A线性无关;有非零解,A线性相关


①n<m:必相关
方程个数<未知数个数,即维数<个数,则线性相关。
n维向量空间,若向量组线性无关,最多只能有n个向量。即维数≥个数。

②n=m:看行列式

③n>m:见定理6、7 + 方程组结论
5.①β可由向量组α₁,α₂,…,αm线性表出 ⇦⇨ An×mx = β 有解 ⇦⇨ r(A)=r(A,β)
②β不可由向量组α₁,α₂,…,αm线性表出 ⇦⇨ An×mx = β 无解 ⇦⇨ r(A)≠r(A,β)

6.向量个数的增减:
①部分相关,整体相关。
②整体无关,部分无关。
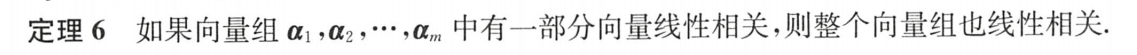

7.维数的增减:
①原来无关,延长必无关 【低维无关,高维无关】
②原来相关,缩短必相关 【高维相关,低维相关】

例题0:张宇30讲 例题3.6 抽象型向量组的线性相关性,用定义法

答案:


例题1:12年05.
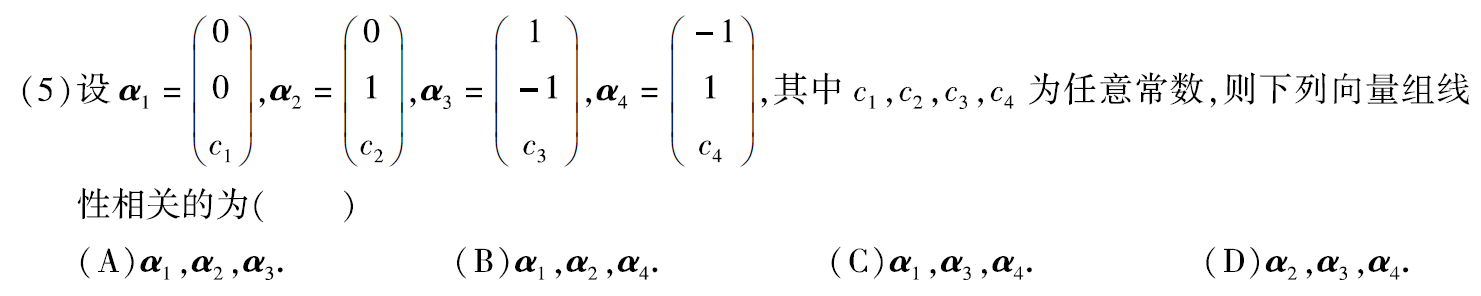
分析:
法一:线性相关的充要条件:线性相关⇦⇨行列式=0
∵|α1,α3,α4|=0,∴α1、α3、α4线性相关
法二:线性相关的充分条件:线性相关⇨成比例
∵α3+α4=(0,0,c3+c4)T,与α1成比例,∴α1、α3、α4线性相关
答案:C
例题2:06年11.

分析:
若已经相关了,则初等变换后依然相关,不能再变回无关了。(若变换后是无关,则变换前肯定也得是无关)
若本来无关,通过变换可能相关。
答案:A
例题3:06年11.真题的变式

答案:C
例题4:14年6. 线性无关、必要性与充分性

分析:
①必要性成立,是必要条件

②充分性不成立,是非充分条件(若向量组中有一个零向量,则该向量组线性相关)

答案:A
3.极大线性无关组、等价向量组、向量组的秩
1.极大线性无关组
(1)概念
①线性无关
②向量组中任意向量均可由极大线性无关组线性表出
(2)性质
①极大线性无关组一般不唯一,但其成员个数是唯一的。极大线性无关组是该向量组的最简小组
②向量组的秩:①极大线性无关组中成员的个数 ②向量组中线性无关的向量个数 ③秩为该向量组所张成的向量空间的维数

(3)找极大线性无关组的步骤
①将列向量们组成矩阵A,作初等行变换化为行阶梯形矩阵,确定r(A)
②按列找出其中一个秩为r(A)的子矩阵,即为一个极大线性无关组
2.等价向量组
1.矩阵等价:①同型 ②秩等:r(A)=r(B)
向量组等价:①同维 ②r(A)=r(B)=r(A,B) ,即两个向量组可以相互线性表出
2.初等行变换:行向量组等价
初等列变换:列向量组等价

等价矩阵和等价向量组

例题1:23李林四(一)5. 向量组等价:型同、秩等、相互表出

分析:

答案:B
例题2:13年5.

答案:B
例题3:00年9.

分析:

答案:D
3.向量组的秩
1.向量组的秩的概念:
①向量组 α 1 , α 2 , . . . , α s α_1,α_2,...,α_s α1,α2,...,αs 的极大线性无关组 α i 1 , α i 2 , . . . , α i r α_{i_1},α_{i_2},...,α_{i_r} αi1,αi2,...,αir 中所含向量的个数r 为 向量组的秩,记作 r ( α 1 , α 2 , . . . , α s ) = r r(α_1,α_2,...,α_s)=r r(α1,α2,...,αs)=r
②向量组中线性无关的向量个数
③秩为该向量组所张成的向量空间的维数
2.性质:
①矩阵的秩 = 行秩 = 列秩 (三秩相等)
②秩大的表示秩小的,可被线性表出的秩小

4.向量空间
(1)向量空间的概念
过渡矩阵、坐标、基、维数
①维数: R n {\rm R}^n Rn 指n维向量空间,由n个线性无关的n维向量张成
②基:证明向量组为R3的基,只需要证明向量组中各向量线性无关
③过渡矩阵: A P = B AP=B AP=B,则 过渡矩阵 P = A − 1 B P=A^{-1}B P=A−1B
④坐标:向量 = 坐标·基

基变换、过渡矩阵

坐标变换

(2)基
向量空间的基的2个必要条件:设V为向量空间,若r个向量α1,α2,…,αr∈V,且满足
(1)α1,α2,…,αr线性无关 【证明向量组为R3的基,只需要证明向量组中各向量线性无关】
(2)V中任意向量都可由α1,α2,…,αr线性表示
则向量组α1,α2,…,αr称为向量空间V的一个基,r称为向量空间V的维数,并称V为r维向量空间
基的概念类似极大线性无关组、基础解系
若把向量空间V看作向量组,则由极大线性无关组的等价定义可知,V的基就是向量组的极大无关组,V的维数就是向量组的秩。
例题:15年20(1)
(3)基变换的过渡矩阵
求A基到B基的过渡矩阵:(右乘列变换)
AP=B,则过渡矩阵 P=A-1B

例题1:03年4.

分析: A P = B ∴ P = A − 1 B AP=B ∴P=A^{-1}B AP=B∴P=A−1B。注意二阶求逆时,先求A*,还要除以|A|。这里|A|=-1
答案: ( 2 3 − 1 − 2 ) \left(\begin{array}{cc} 2 & 3 \\ -1 & -2 \end{array}\right) (2−13−2)
例题2:19年20.

分析:
(2)①证明3个向量是R3的基,只需证明它们线性无关 [向量的基线性无关]
②求A基到B基的过渡矩阵:
AP=B,则过渡矩阵 P=A-1B
答案:

(4)向量在基下的坐标
向量 = 坐标·基
例题0:

例题1:23李林四(二)15.
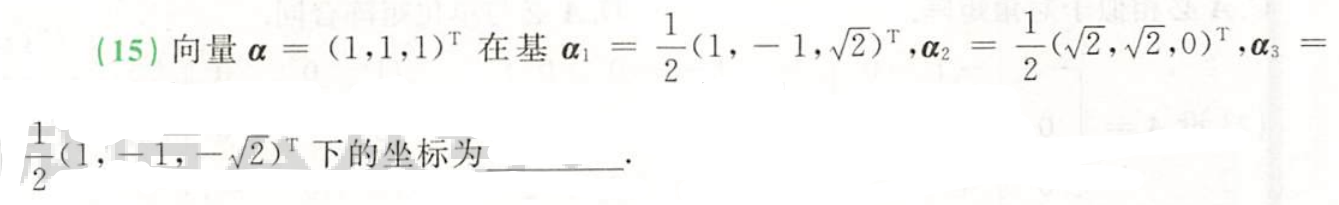
分析:

答案: ( 2 2 , 2 , − 2 2 ) (\dfrac{\sqrt{2}}{2},\sqrt{2},-\dfrac{\sqrt{2}}{2}) (22,2,−22)
例题2:15年20.

分析:
(1)证明向量组是R3的一个基,只需要证明向量组线性无关
(2)坐标
第4章 线性方程组

(一)具体型线性方程组

1.齐次线性方程组 Ax=0
齐次线性方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0
m为所给方程个数,n为未知数个数。m<n时就有自由变量
例题:18年20.(1)
(1)有解的条件:齐次线性方程组解的判别
AX=0,齐次必然有解。
① r ( A ) = n r(A)=n r(A)=n ( α 1 , α 2 , . . . , α n α_1,α_2,...,α_n α1,α2,...,αn线性无关):唯一零解。
② r ( A ) < n r(A)<n r(A)<n ( α 1 , α 2 , . . . , α n α_1,α_2,...,α_n α1,α2,...,αn线性相关):无穷多个非零解 和零解 。且有n-r个线性无关解 (用这n-r个线性无关解,来表示这无穷多个解)

A x = 0 Ax=0 Ax=0的无穷多解是一个“解空间”,用 k 1 ξ 1 + k 2 ξ 2 + . . . , k n − r ξ n − r k_1ξ_1+k_2ξ_2+...,k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...,kn−rξn−r表示(s=n-r)
(2)解的性质:齐次解的性质
解的叠加性:解的线性组合也是解
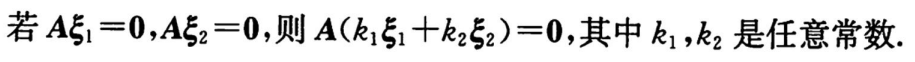
(3)基础解系、通解的结构
①基础解系
1.基础解系的定义:
设 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r满足
①是方程组 A x = 0 Ax=0 Ax=0的解
②线性无关
③有s=n-r个。方程组 A x = 0 Ax=0 Ax=0的任一解向量均可由 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r线性表出
则称 ξ 1 , ξ 2 , . . . , ξ n − r ξ_1,ξ_2,...,ξ_{n-r} ξ1,ξ2,...,ξn−r 为 A x = 0 Ax=0 Ax=0 的基础解系。
基础解系是齐次方程组 A x = 0 Ax=0 Ax=0 的解向量集合的极大线性无关组。
2.基础解系的求法:见(4)求解方法与步骤的前三步
②通解的结构
(1)齐次
①先求出 n − r ( A ) n-r(A) n−r(A)个线性无关的基础解系
②每一个基础解系前面加一个 k i k_i ki,基础解系的线性组合即为齐次线性方程组的通解。
则齐次方程组的通解为: X = k 1 ξ 1 + k 2 ξ 2 + k 3 ξ 3 + . . . k n − r ξ n − r X=k_1ξ_1+k_2ξ_2+k_3ξ_3+...k_{n-r}ξ_{n-r} X=k1ξ1+k2ξ2+k3ξ3+...kn−rξn−r
(2)非齐次
若非齐次方程组 A X = β AX=β AX=β的特解为 β β β,则非齐次方程组的通解为: X = k 1 ξ 1 + k 2 ξ 2 + k 3 ξ 3 + . . . + . . . + k n − r ξ n − r + β X=k_1ξ_1+k_2ξ_2+k_3ξ_3+...+...+k_{n-r}ξ_{n-r}+β X=k1ξ1+k2ξ2+k3ξ3+...+...+kn−rξn−r+β
通解形成“s维解空间”,s=n-r
③自由变量
(1)谁是自由变量:化行阶梯/行最简矩阵时,不在直角边上的 x i x_i xi为自由变量
(2)自由变量/线性无关的解向量的个数: n − r ( A ) n-r(A) n−r(A)
(3)自由变量的设置:
①1个自由变量:1
②2个自由变量: ( 1 0 ) , ( 0 1 ) \binom{1}{0},\binom{0}{1} (01),(10)
③3个自由变量: ( 1 0 0 ) \left(\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right) 100 , ( 0 1 0 ) \left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right) 010 , ( 0 0 1 ) \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right) 001
例题1:14年20

分析:
(2)A3×4B4×3=E3×3
由于A和B都不是方阵,故AB都不可逆,更没有行列式。
考虑拆分,B=(b1,b2,b3),E=(e1,e2,e3)。则AB=E被拆成Ab1=e1,Ab2=e2,Ab3=e3
bi=kiξ+特解,k为任意常数
(4)求解方法和步骤
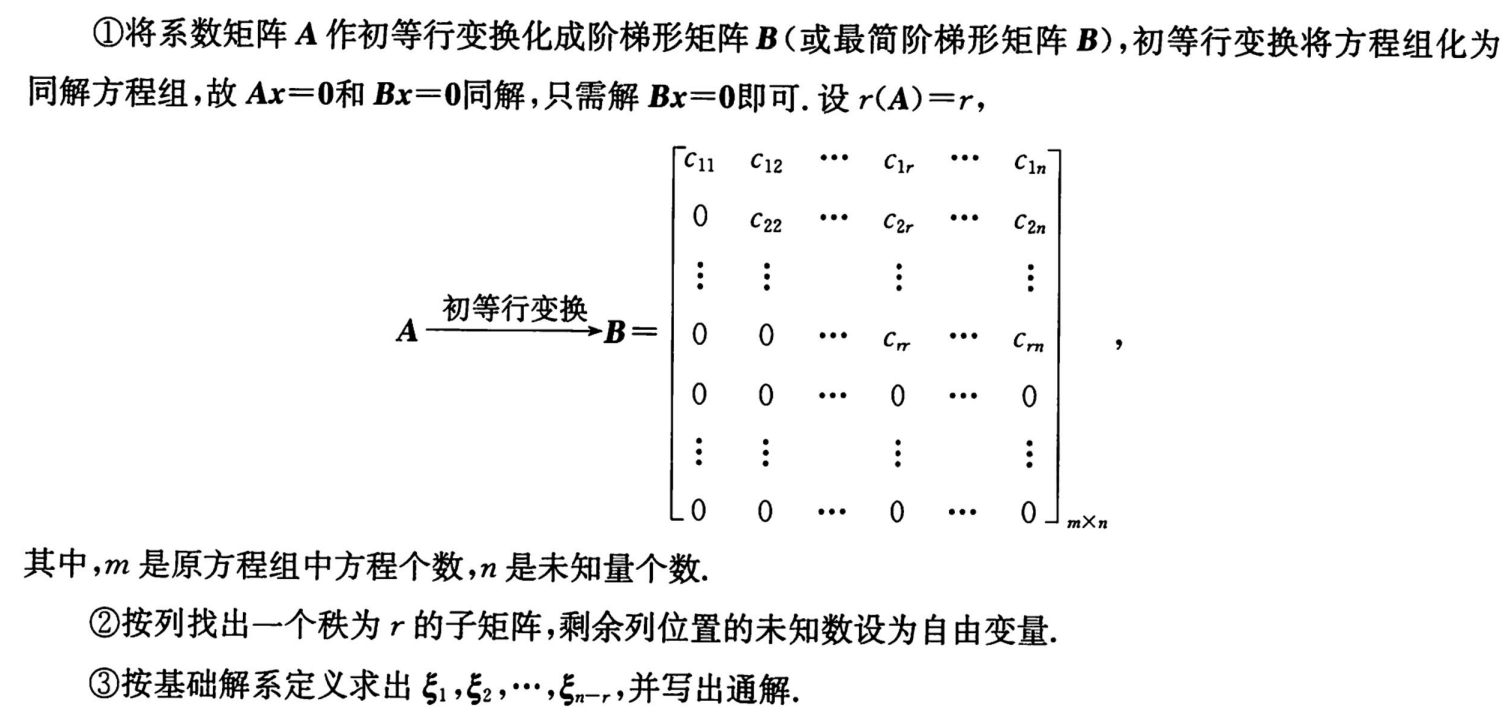
2.基础解系(前3步)、通解求法:
①把A化为行阶梯/行最简矩阵 (方程组经初等行变换转化为同解方程组)
②找出一个秩为r=r(A)的子矩阵,基础解系为s=n-r个,把n-r(A)个 x i x_i xi设为自由变量。(有同阶的才能设为自由变量)
(例如n=5,r(A)=3,s=n-r=5-3=2,基础解系有2个成员 ξ 1 , ξ 2 ξ_1,ξ_2 ξ1,ξ2
设 x 4 , x 5 x_4,x_5 x4,x5为自由变量,则 ξ 1 , ξ 2 ξ_1,ξ_2 ξ1,ξ2的最后两维:(1,0) (0,1),即 ξ 1 = ( , , 1 , 0 ) T , ξ 2 = ( , , 0 , 1 ) T ξ_1=( , , 1,0)^T,ξ_2=( , , 0,1 )^T ξ1=(,,1,0)T,ξ2=(,,0,1)T。
③根据行阶梯/行最简矩阵,由最后一行倒着开始求其余变量的值,直至第一行,求出一个解向量 ξ 1 ξ_1 ξ1;再从最后一行开始求,得到第二个解向量 ξ 2 ξ_2 ξ2;直至求完所有解向量 ξ n − r ξ_{n-r} ξn−r
④齐次线性方程组的通解为: k 1 ξ 1 + k 2 ξ 2 + . . . + k n − r ξ n − r k_1ξ_1+k_2ξ_2+...+k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...+kn−rξn−r

例题1:19年13.
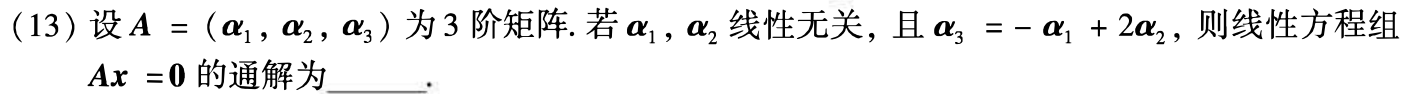
分析:

答案: X = k ( 1 − 2 1 ) X=k\left(\begin{array}{c} 1 \\ -2 \\ 1 \end{array}\right) X=k 1−21 ,k为任意常数
2.非齐次线性方程组 Ax=β
非齐次线性方程组 Am×nx=β,可组合成AX=B
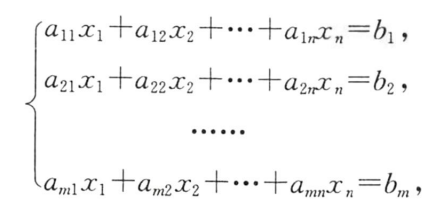
①方程组形式: A X = β AX=β AX=β
②向量形式: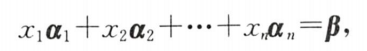
①方程组的解 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn,就是向量与向量之间的表示系数
②齐次线性方程组Ax=0,称为非齐次线性方程组Ax=β的导出组
(1)有解的条件:非齐次线性方程组解的判别
① r ( A ) ≠ r ( A , β ) r(A)≠r(A,β) r(A)=r(A,β) (即 r(A)+1=r(A,β),β不能由α₁,α₂,α₃线性表示):非齐次线性方程组无解,
② r ( A ) = r ( A , β ) r(A)=r(A,β) r(A)=r(A,β) (β可由α₁,α₂,α₃线性表示):非齐次线性方程组 AX=β有解,
③ r ( A ) = r ( A , β ) = n r(A)=r(A,β)=n r(A)=r(A,β)=n (β可由α₁,α₂,…,αn线性表示且表示法唯一):非齐次线性方程组有唯一解,
④ r ( A ) = r ( A , β ) < n r(A)=r(A,β)<n r(A)=r(A,β)<n (β可由α₁,α₂,…,αn线性表示且表示法不唯一):非齐次线性方程组有无穷多解
(2)解的性质:非齐次解的性质
①非齐次特解做差,是齐次特解
②非齐次通解:齐次通解 + 非齐次特解

(3)求解方法和步骤
①求齐次方程组的基础解系,进而求齐次方程组的通解 k 1 ξ 1 + k 2 ξ 2 + . . . k n − r ξ n − r k_1ξ_1+k_2ξ_2+...k_{n-r}ξ_{n-r} k1ξ1+k2ξ2+...kn−rξn−r 【注意,基础解系是齐次的,等式右边为0】
②求特解 η η η:令自由项均为0,等式右边为自由项 β i β_i βi。从最后一行开始,代入求解,直至第一行
③拼起来,即为非齐通解
例题1:23李林六套卷(二)15.
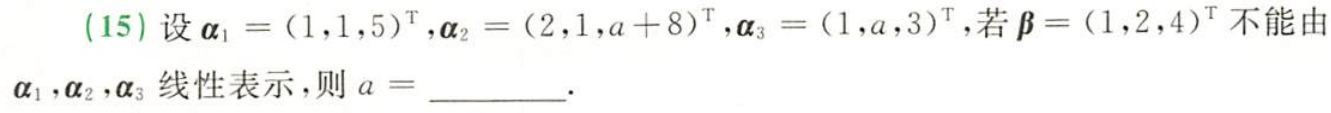
分析:β不能由α₁,α₂,α₃线性表示,即非齐次线性方程组无解, r ( A ) ≠ r ( A , β ) r(A)≠r(A,β) r(A)=r(A,β)

答案:0
例题2:12年20(2)

分析:
(2)Ax=β有无穷多解,则 r ( A ) = r ( A ˉ ) < n r(A)=r(\bar{A})<n r(A)=r(Aˉ)<n,即r(A)<n,即 |A|=0
化为行最简后,先求齐次解Ax=0得基础解系ξ=(1,1,1,1)T。特解即为此时的β’=(0,-1,0,0)T。通解X=kξ+β’=k(1,1,1,1)T+(0,-1,0,0)T,k为任意常数
例题3:13年20.

分析:设 C = ( x 1 x 2 x 3 x 4 ) C=\left(\begin{array}{cc} x_1 & x_2 \\ x_3 & x_4 \end{array}\right) C=(x1x3x2x4),由AC-CA=B得出含x的方程组,写为系数矩阵D的增广矩阵 D ˉ \bar{D} Dˉ,化为行最简矩阵。这时就可以通过非齐次线性方程组解的判别条件 r ( D ) = r ( D ˉ ) r(D)=r(\bar{D}) r(D)=r(Dˉ)来求a,b的值了。求出后把a,b代入 D ˉ \bar{D} Dˉ,求出齐次方程组的基础解析 ξ 1 = ( 1 − 1 1 0 ) ξ_1=\left(\begin{array}{c} 1 \\ -1 \\ 1 \\ 0 \end{array}\right) ξ1= 1−110 , ξ 2 = ( 1 0 0 1 ) ξ_2=\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 1 \end{array}\right) ξ2= 1001 ,非齐次通解X= ( x 1 x 2 x 3 x 4 ) = k 1 ξ 1 + k 2 ξ 2 + ( 1 0 0 0 ) \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right)=k_1ξ_1+k_2ξ_2+\left(\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\right) x1x2x3x4 =k1ξ1+k2ξ2+ 1000
∴ C = ( x 1 x 2 x 3 x 4 ) C=\left(\begin{array}{cc} x_1 & x_2 \\ x_3 & x_4 \end{array}\right) C=(x1x3x2x4)=…
(4)非齐次线性方程组的几何意义:3个方程代表3个平面,交点代表解的个数
方程组有3个方程,每个方程代表一个平面。3个平面的交点个数代表方程组的解的个数。
若三个平面相交于同一条直线,则 r ( A ) = r ( A ˉ ) = 2 r(A)=r(\bar{A})=2 r(A)=r(Aˉ)=2

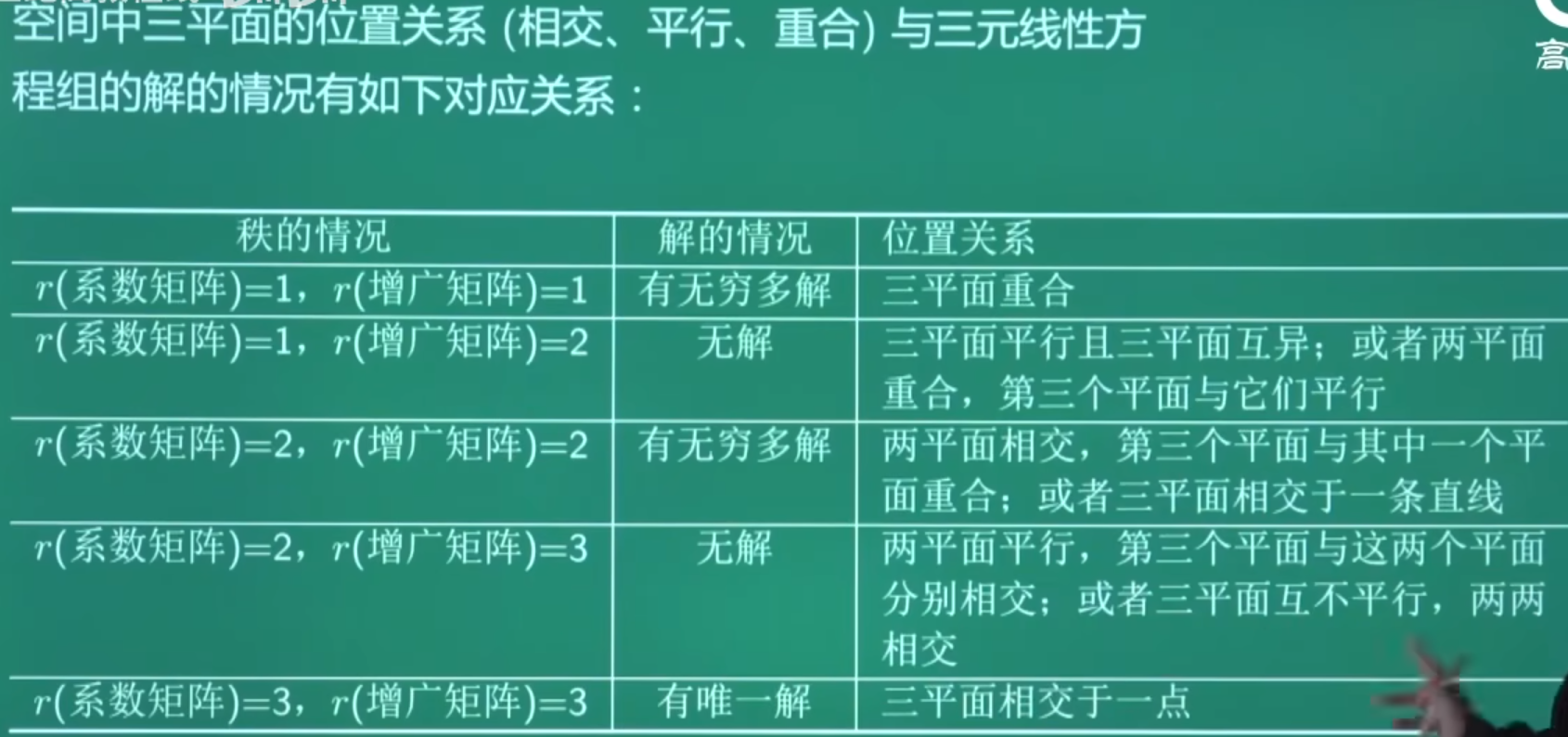
例题1:23李林六套卷(三)7.

分析:3个平面相较于一条直线,则有无穷多个交点,则 r ( A ) = r ( A ˉ ) < 3 r(A)=r(\bar{A})<3 r(A)=r(Aˉ)<3
A ˉ = ( 1 1 b ∣ 3 2 a + 1 b + 1 ∣ 7 0 1 − a 2 b − 1 ∣ 0 ) \bar{A}=\left(\begin{array}{cc} 1 & 1 & b &| \ 3 \\ 2 & a+1 & b+1 &| \ 7 \\ 0 & 1-a & 2b-1 &| \ 0\\ \end{array}\right) Aˉ= 1201a+11−abb+12b−1∣ 3∣ 7∣ 0
显然,第三行要为全0,则a=1,b=1/2
答案:B
例题2:02年10. 系数矩阵秩、增广矩阵秩 用空间中的平面表示
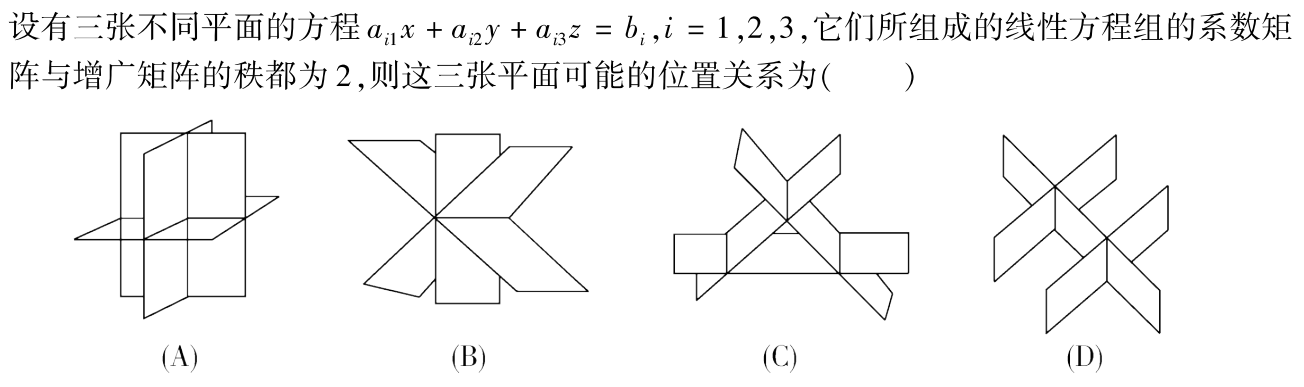
分析:
A.三个平面只有一个交点,方程组有唯一解, r ( A ) = r ( A ˉ ) = 3 r(A)=r(\bar{A})=3 r(A)=r(Aˉ)=3。A❌
B.三个平面相较于同一条直线,即方程组有无穷多个解, r ( A ) = r ( A ˉ ) = 2 < 3 r(A)=r(\bar{A})=2<3 r(A)=r(Aˉ)=2<3。B✔
C.两两相交,互不平行: r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3。 C❌
D.两平面平行,第三个平面与这两个平行平面分别相交: r ( A ) = 2 , r ( A ˉ ) = 3 r(A)=2,r(\bar{A})=3 r(A)=2,r(Aˉ)=3。D❌
答案:B
例题3:19年6.

答案:A
(二)抽象型线性方程组



4.解就是系数

例题1:基础30讲线代分册 求非齐次线性方程组的通解、解的性质

分析:
①非齐通的解结构:非齐通 = 齐通 + 非齐特
②解的性质:i. η 1 − η 2 η_1-η_2 η1−η2为齐次特解 ii. 1 2 ( η 1 + η 2 ) \dfrac{1}{2}(η_1+η_2) 21(η1+η2)为非齐次特解, 1 3 ( η 3 + 2 η 2 ) \dfrac{1}{3}(η_3+2η_2) 31(η3+2η2)为非齐次特解 iii. 1 2 ( η 1 + η 2 ) − 1 3 ( η 3 + 2 η 2 ) \dfrac{1}{2}(η_1+η_2)-\dfrac{1}{3}(η_3+2η_2) 21(η1+η2)−31(η3+2η2)也为齐次通解,乘6倍后 3 ( η 1 + η 2 ) − 2 ( η 3 + 2 η 2 ) 3(η_1+η_2)-2(η_3+2η_2) 3(η1+η2)−2(η3+2η2)仍为齐次通解
本题不必求出 η 1 , η 2 , η 3 η_1,η_2,η_3 η1,η2,η3各自的值
答案:
例题2:
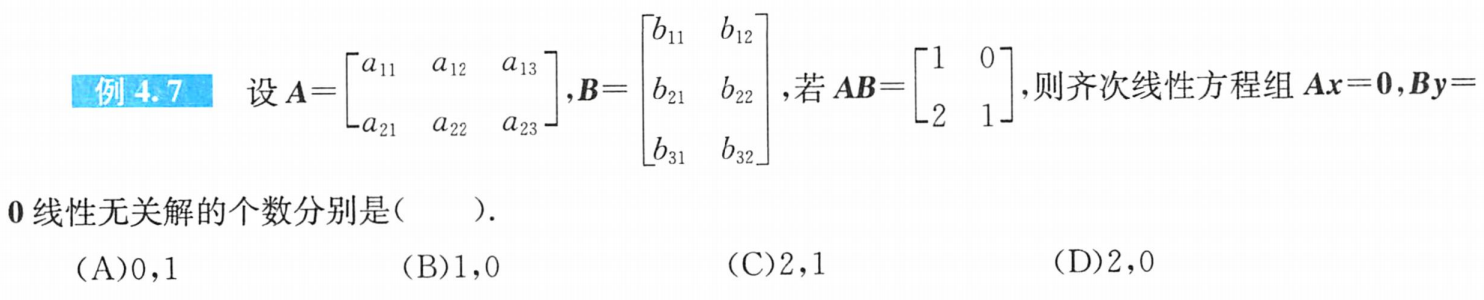
分析:
① r ( A B ) ≤ m i n { r ( A ) , r ( B ) } r(AB)≤min\{ r(A),r(B)\} r(AB)≤min{r(A),r(B)}:由题得r(AB)=2≤min{ r(A),r(B} ∴r(A)≥2,r(B)≥2
又∵秩=行秩=列秩≤min{m,n},∴r(A)≤2,r(B)≤2
故r(A)=r(B)=2
②线性无关解的个数 s = n − r s=n-r s=n−r
s A = n A − r ( A ) = 3 − 2 = 1 s_A=n_A-r(A)=3-2=1 sA=nA−r(A)=3−2=1
s B = n B − r ( B ) = 2 − 2 = 0 s_B=n_B-r(B)=2-2=0 sB=nB−r(B)=2−2=0
答案:B
例题3:

分析:
①s=n-r(A)=1 ∴r(A)=3 ∴r(A*)=1 ∴s*=n-r(A*)=3 排除AB
②(1,0,1,0)T是Ax=0的一个基础解系(其中A=(α₁,α₂,α₃,α₄)),即α₁+α₃=0,即α₁与α₃能相互线性表示,线性相关。故A*x=0的基础解系只能选 124或234。选D
答案:D
例题4:

答案:

(三)方程组的公共解、同解方程组
1.方程组的公共解
①齐次线性方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0和 B m × n x = 0 B_{m×n}x=0 Bm×nx=0的公共解,是满足方程组 [ A B ] x = 0 \left[\begin{array}{ccc}A\\B\end{array}\right]x=0 [AB]x=0的解,即联立求解
②增加约束,使其相等:令 k 1 ξ 1 + k 2 ξ 2 = l 1 η 1 + l 2 η 2 k_1ξ_1+k_2ξ_2=l_1η_1+l_2η_2 k1ξ1+k2ξ2=l1η1+l2η2,找到k1k2关系,将二维解空间化为一维解空间
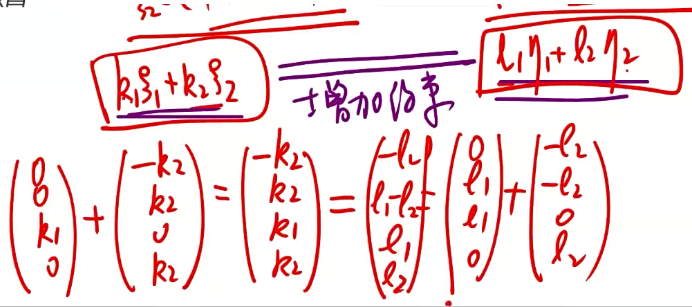

2.同解方程组
1.定义/概念:两个方程组 A m × n x = 0 A_{m×n}x=0 Am×nx=0 和 B m × n x = 0 B_{m×n}x=0 Bm×nx=0 有完全相同的解,则称它们为同解方程组
2.性质:
A x = 0 Ax=0 Ax=0 与 B x = 0 Bx=0 Bx=0 为同解方程组
⇦⇨解完全相同:即Ax=0的解满足Bx=0,且Bx=0的解满足Ax=0 (互相把解代入,求出结果即可)
⇦⇨A与B的行向量组为等价向量组
⇦⇨ r ( A ) = r ( B ) = r ( A B ) r(A)=r(B)=r\dbinom{A}{B} r(A)=r(B)=r(BA)

例题1:

例题2:设Am×n,证明r(A)=r(ATA)

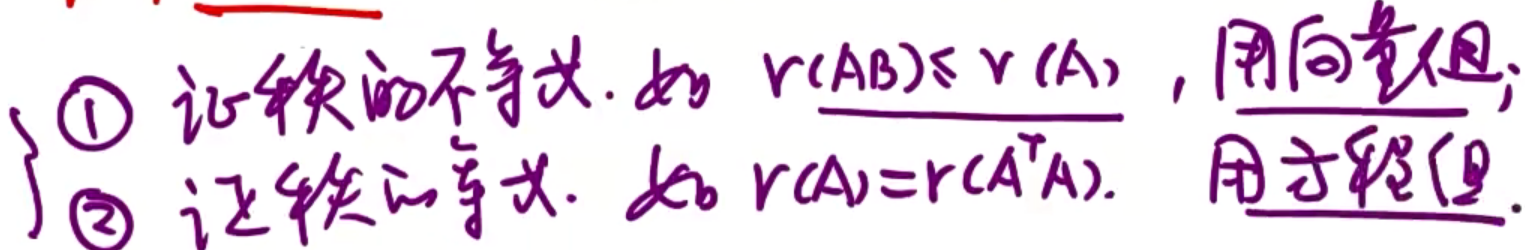
证明:

∴r(A)=r(AT)=r(ATA)=r(AAT),对任意Am×n均成立
例题3:22年6.

分析:
①仅有零解 ⇦⇨ 系数矩阵满秩
②齐次方程组的同解变形 ⇦⇨ 矩阵的初等行变换

答案:C
相关文章:

线性代数(主题篇):第三章:向量组 、第四章:方程组
文章目录 第3章 n维向量1.概念(1)n维单位列向量 2.向量、向量组的的线性关系(线性相关性)(1)线性表示 :AXβ(2)线性相关、线性无关: AX0①线性相关②线性无关③线性相关性7大定理 3.极大线性无关组、等价向量组、向量组的秩1.极大线性无关组2.等价向量组…...

大数据课程C4——ZooKeeper结构运行机制
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Zookeeper的特点和节点信息; ⚪ 掌握Zookeeper的完全分布式安装 ⚪ 掌握Zookeeper的选举机制、ZAB协议、AVRO; 一、Zookeeper-简介 1. 特点…...

解决伪类元素‘after‘或者‘before‘遮挡父元素,导致鼠标移入或点击等事件不生效的问题
第一种调整css的index值 如果对显示没有影响的话,可以这么做 第二种设置css属性:pointer-event:none 原理是: 对一个元素设置 pointer-events: none,能让浏览器在处理鼠标操作时,忽视掉这个元素的存在&a…...

电动汽车市场的减速,正在让小鹏汽车付出代价
来源:猛兽财经 作者:猛兽财经 总结: (1)由于价格压力上升、竞争加剧和需求减弱,小鹏汽车的交付量出现了明显下滑,6月份的交付量已经同比下降了43%。 (2)小鹏汽车对2023年…...

Yarn上Streaming流自动调节资源设计
Streaming流自动调节资源 自动资源调节简单来说就是根据数据的输入速率和数据的消费速率来判断是否应该调节资源。如果输入速率大于消费速率,并且在输入速率还在攀升,则将该Job停止并调高Job的资源等级然后重启。如果消费速率大于输入速率,并…...

微信小程序的个人博客--【小程序花园】
微信目录集链接在此: 详细解析黑马微信小程序视频–【思维导图知识范围】难度★✰✰✰✰ 不会导入/打开小程序的看这里:参考 让别人的小程序长成自己的样子-更换window上下颜色–【浅入深出系列001】 文章目录 本系列校训啥是个人博客项目里的理论知识…...

智慧园区楼宇合集 | 图扑数字孪生管控系统
智慧园区是指将物联网、大数据、人工智能等技术应用于传统建筑和基础设施,以实现对园区的全面监控、管理和服务的一种建筑形态。通过将园区内设备、设施和系统联网,实现数据的传输、共享和响应,提高园区的管理效率和运营效益,为居…...
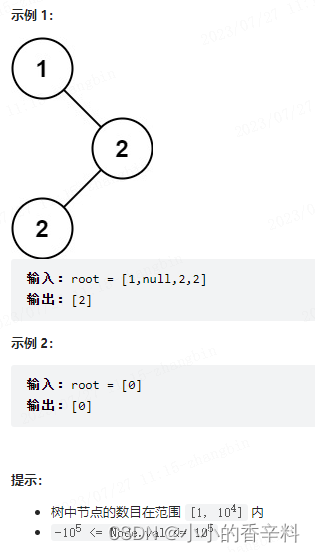
【代码随想录day21】二叉搜索树中的众数
题目 给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 如果树中有不止一个众数,可以按 任意顺序 返回。 假定 BST 满足如下定义&am…...
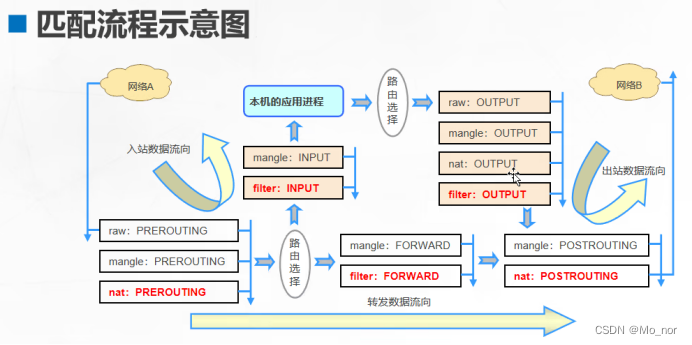
【防火墙】iptables防火墙(一)
防火墙具有隔离功能 主要部署在网络边缘或者主机边缘,防火墙的主要作用是决定哪些数据可以被外网访问,哪些数据可以进入内网访问 网络层(路由器):数据的转发 安全技术 1.入侵监测系统:在检测到威胁&…...

微信小程序之富文本特殊处理
文章目录 前言一、video的处理二、img的处理总结 前言 小程序中使用富文本编辑器,由于rich-text受限 部分富文本内容无法渲染或排版错乱。以img和video为例,处理起来让人头疼。网上各种长篇大论,实际上没有任何帮助。接下来我们就一起聊聊im…...
react-draft-wysiwyg富文本编辑器
在React项目中使用 yarn add react-draft-wysiwyg draft-js or npm i react-draft-wysiwyg draft-js推荐在项目中单独创建一个富文本编辑器组件 import { Editor } from "react-draft-wysiwyg"; import { EditorState, convertToRaw, ContentState } from draft-js…...

P5721 【深基4.例6】数字直角三角形
【深基4.例6】数字直角三角形 题目描述 给出 n n n,请输出一个直角边长度是 n n n 的数字直角三角形。所有数字都是 2 2 2 位组成的,如果没有 2 2 2 位则加上前导 0 0 0。 输入格式 输入一个正整数 n n n。 输出格式 输出如题目要求的数字直…...

【电子设计大赛】2023 年全国大学生电子设计竞赛 仪器和主要元器件清单
2023 年全国大学生电子设计竞赛仪器设备和主要元器件及器材清单 [本科组] 1. 仪器设备清单 直流稳压电源(具有恒流/恒压模式自动切换功能,0~30V/3A,双路) 数字示波器(100MHz, 双通道) 函数发…...
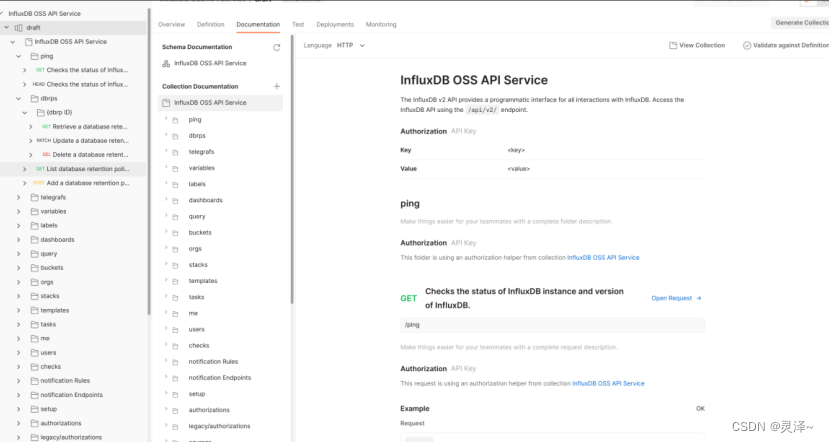
(八九)如何与InfluxDB交互InfluxDB HTTP API
以下内容来自 尚硅谷,写这一系列的文章,主要是为了方便后续自己的查看,不用带着个PDF找来找去的,太麻烦! 第 8 章 前言:如何与InfluxDB交互 1、InfluxDB启动后,会向外提供一套HTTP API。外部程…...
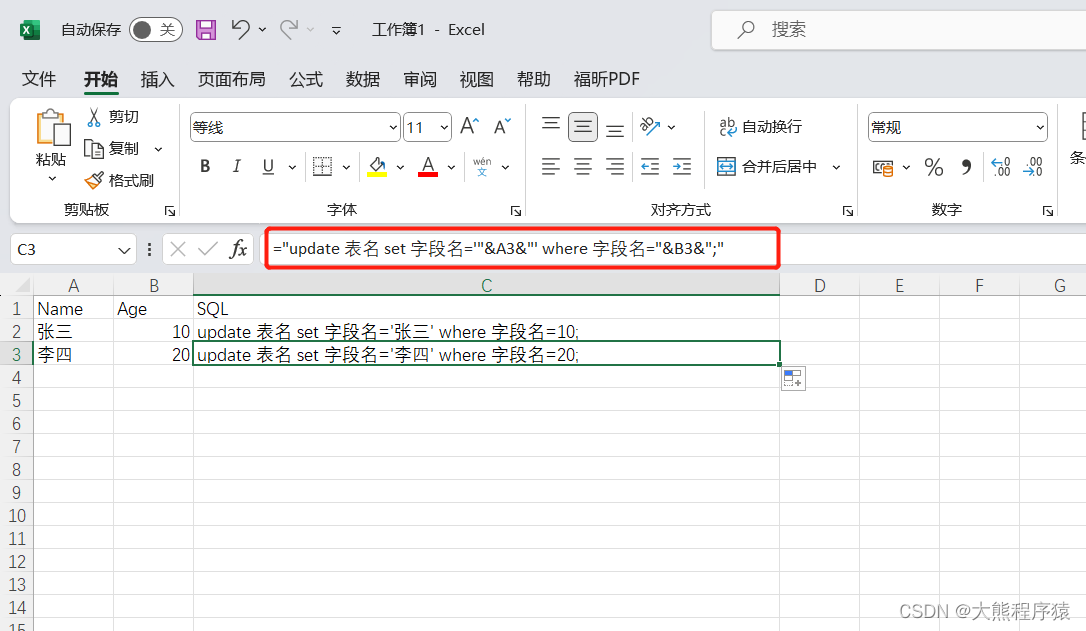
excel 生成sql技巧
"update 表名 set 字段名"&A2&" where 字段名"&B2&";"...
)
2023牛客暑期多校训练营2(D/E/F/H/I/K)
目录 D.The Game of Eating E.Square F.Link with Chess Game H.0 and 1 in BIT I.Link with Gomoku K.Box D.The Game of Eating 思路:倒着贪心。因为正着贪会导致一种局面:我选了当前喜爱值最大的菜,但是就算我不选这个菜࿰…...

Ubuntu搭建Samba服务-学习记录
文章目录 Ubuntu安装Samba流程Samba配置文件Samba添加账户配置文件修改Samba服务控制设置开机自动启动通过systemctl 启动服务通过 rc.local 启动 Windows访问参考链接 当前文章仅用于记录,在 Ubuntu中安装使用Samba,在Windows访问 系统环境:…...
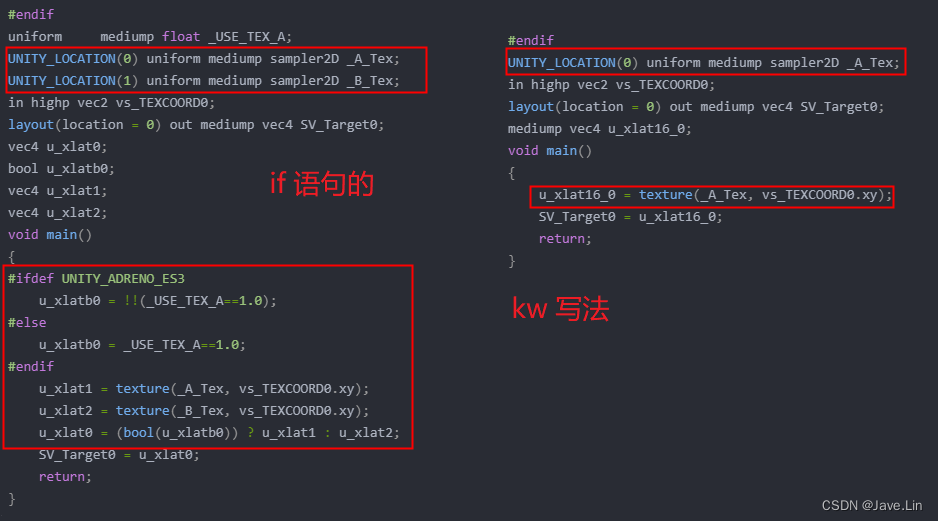
Unity Shader - if 和 keyword 的指令比较
文章目录 环境TestingIf4Sampleunity shaderlab 中的 TestingIf4Sample.shadergraphics analyzer 中的 TestingIf4Sample.glsl TestingKW4Sampleunity shaderlab 中的 TestingKW4Sample.shadergraphics analyzer 中的 TestingKW4Sample.glsl 比较 环境 Unity : 2020.3.37f1 Pi…...
【C++入门到精通】C++入门 —— 类和对象(了解类和对象)
目录 一、类和对象的历史由来 二、面向过程和面向对象的初步认识 三、类 1.引子 2.类的定义 3.类的访问限定符及封装 ⭕访问限定符 🚩访问限定符解释说明 🚩struct 与 class 的区别 1. 默认访问级别: 2. 继承权限(默认的…...
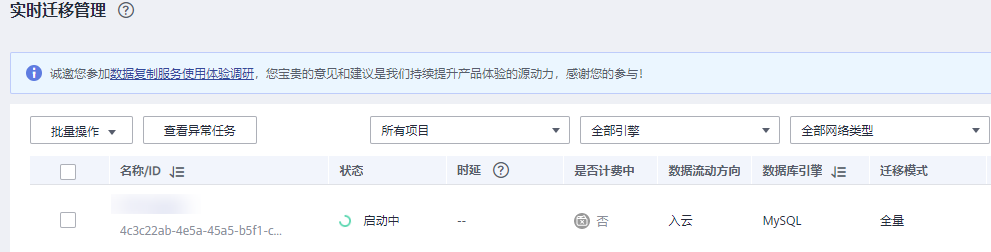
DRS 迁移本地mysql 到华为云
准备工作: 源端的IP地址(公网),用户明和密码。如果通过公网迁移,需要在安全组放通drs访问源端数据库的3306端口。目标端的IP地址,用户名和密码。 创建DRS迁移任务 创建迁移任务 登录华为云控制台。单击管…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...