【动态规划刷题 1 】 第N个泰波那契数 三步问题
第N个泰波那契数
链接: 第N个泰波那契数
1137 . 第 N 个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
示例 2:
输入:n = 25
输出:1389537
1.状态表示
dp[i] 表示的是第 i 个泰波那契数的值。
2.状态转移方程
动态规划题,我们需要学会依靠经验和题目解析去猜测他们的状态转移方程。
这一题题目已经告诉我们了。
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
3. 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因为dp[i-2] 或 dp[i-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将0, 1, 2 位置的值初始化。题⽬中已经告诉我们
dp[0] = 0, dp[1] = dp[2] = 1 。
4. 填表顺序
按照数组下标的顺序,从左往右。
5. 返回值
应该返回 dp[n] 的值。
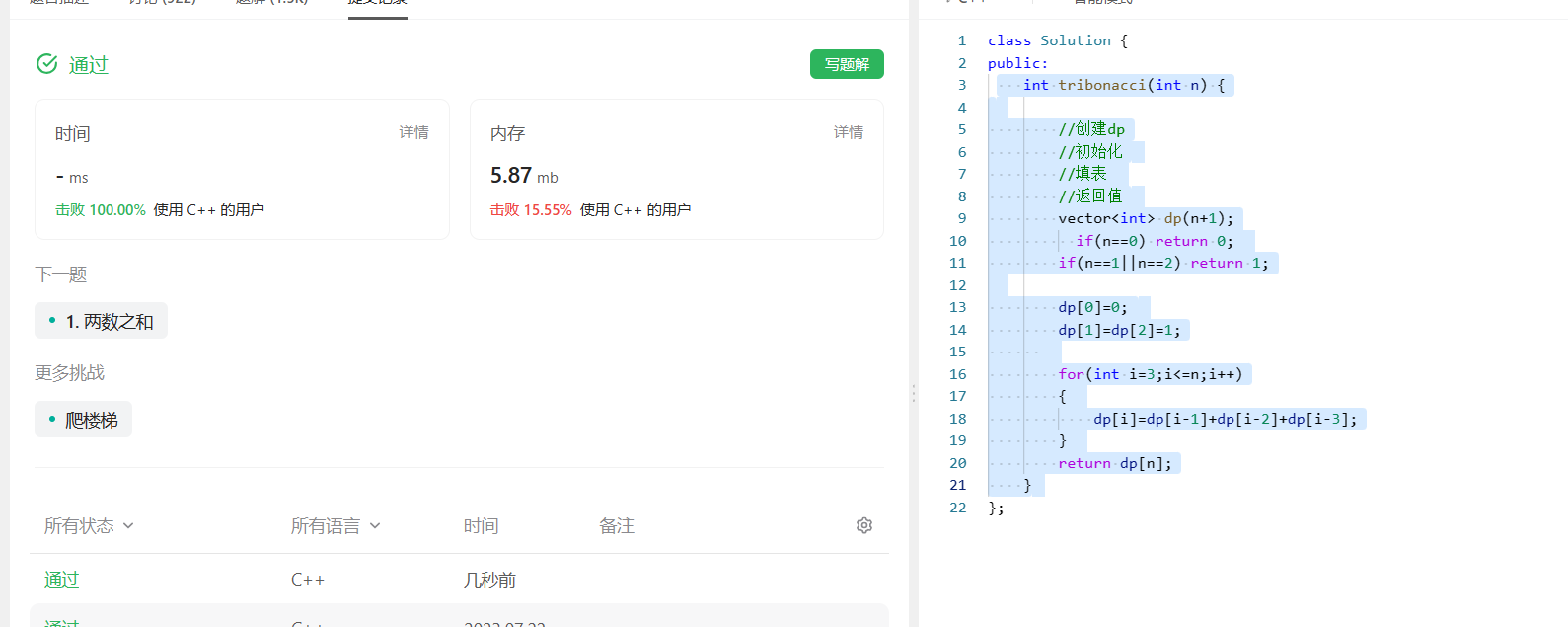
代码:
在写代码时按照此顺序:
- 创建dp
- 初始化
- 填表
- 返回值
int tribonacci(int n) {vector<int> dp(n+1);if(n==0) return 0;if(n==1||n==2) return 1;dp[0]=0;dp[1]=dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
三步问题
链接: 三步问题
面试题 08.01. 三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
1.状态表示
dp[i] 表示的是以 i 阶楼梯为结尾,小孩跳动到此处的方式数。
2.状态转移方程
以i位置状态的最近的⼀步,来分情况讨论:
如果 dp[i] 表⽰⼩孩上第 i 阶楼梯的所有⽅式,那么它应该等于所有上⼀步的⽅式之和:
- 从 i-1 处跳⼀级台阶, dp[i] += dp[i - 1] ;
- 从 i-2 处跳两级台阶, dp[i] += dp[i - 2] ;
- 从 i-3 处跳三级台阶, dp[i] += dp[i - 3] ;
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
3. 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因为dp[i-2] 或 dp[i-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将0, 1, 2 位置的值初始化。我们可知
dp[1] = 1, dp[2] = 2,dp[3]=4;
4. 填表顺序
按照数组下标的顺序,从左往右。
5. 返回值
应该返回 dp[n] 的值。
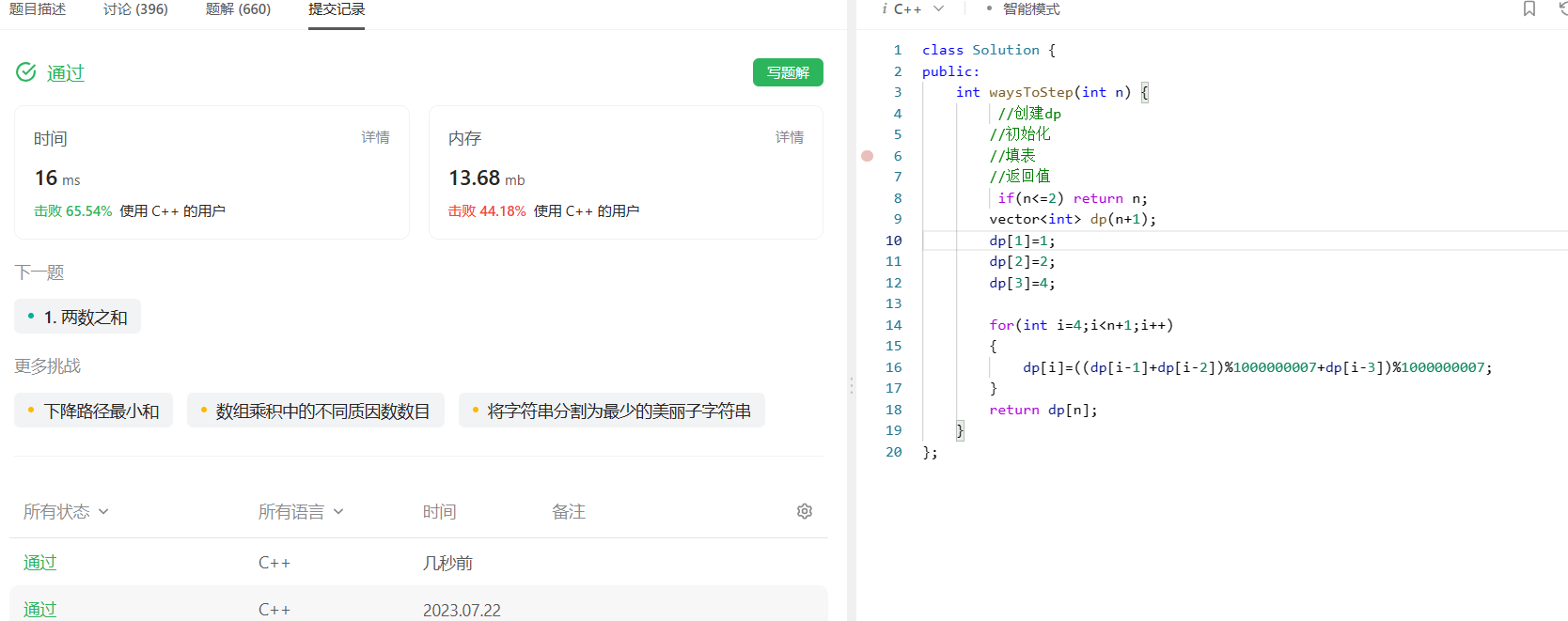
代码
此题会存在数据溢出的问题,需要取模处理:
int waysToStep(int n) {//创建dp//初始化//填表//返回值if(n<=2) return n;vector<int> dp(n+1);dp[1]=1;dp[2]=2;dp[3]=4;for(int i=4;i<n+1;i++){//取模dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;}return dp[n];}
相关文章:

【动态规划刷题 1 】 第N个泰波那契数 三步问题
第N个泰波那契数 链接: 第N个泰波那契数 1137 . 第 N 个泰波那契数 泰波那契序列 Tn 定义如下: T0 0, T1 1, T2 1, 且在 n > 0 的条件下 Tn3 Tn Tn1 Tn2 给你整数 n,请返回第 n 个泰波那契数 Tn 的值。 示例 1: 输入:…...

【踩坑】三种方式解决 Homebrew failing to install - fatal: not in a git directory
问题描述 解决方法一 添加安全目录,没有测试。 git config --global --add safe.directory /opt/homebrew/Library/Taps/homebrew/homebrew- git config --global --add safe.directory /opt/homebrew/Library/Taps/homebrew/homebrew-cask 解决方法二 取消挂载这…...

零信任安全解决方案
什么是零信任 零信任网络架构 (ZTNA) 或零信任安全是一种新的组织网络安全方法。它旨在修复传统基于边界的安全性中的缺陷并简化网络设计。 它以“永不信任,始终验证”的原则运作。这意味着,无论用户或设备位于何处,…...

如何创建高级 CSS 下拉菜单
效果展示 实现思路及部分代码 1、定义整体页面结构 从上述的效果展示图可以看出,页面的整体结构应该需要一个总菜单容器来装载父级菜单项,并且对应的父级菜单项应该有对应的菜单子项。子菜单是分类的话,我们还需要额外在扩展对应的容器来装…...
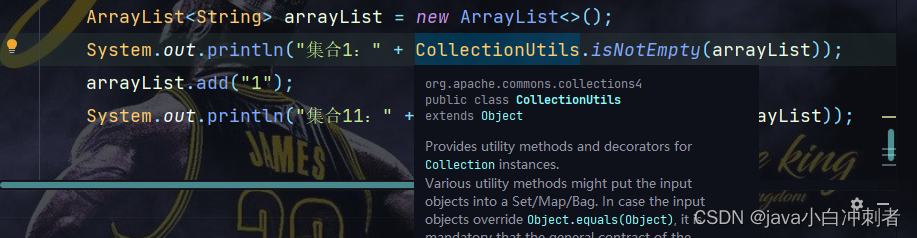
java中判断list是否为空
java中判断list是否为空是日常代码中经常遇到的问题。最近发现一个Utils提供的方法可以一步判断。 废话不多说,直接上代码! ArrayList<String> arrayList new ArrayList<>(); System.out.println("集合1:" Collecti…...

龙芯3A5000板卡在高性能工作站的应用方案-迅为电子
将龙芯3A5000应用于高性能工作站时,可以考虑以下方案: 多核计算能力:龙芯3A5000拥有多核心处理器,具备强大的计算能力。在高性能工作站中,可以利用多核心的处理能力来支持复杂的工程设计、科学计算和数据处理任务。…...

WebSocket心跳机制
WebSocket是HTML5开始提供的一种浏览器与服务器进行全双工通讯的网络技术,属于应用层协议。 WebSocket 使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。 1、创建webSocket // Create WebSocket connection. const sock…...
Form Generator 扩展子表单组件之表单校验(超详细)
一、form-generator是什么?✨ ⭐️ 🌟 form-generator的作者是这样介绍的:Element UI表单设计及代码生成器,可将生成的代码直接运行在基于Element的vue项目中;也可导出JSON表单,使用配套的解析器将JSON解析成真实的表单。 但目前它提供的组件并不能满足我们在项目中的…...
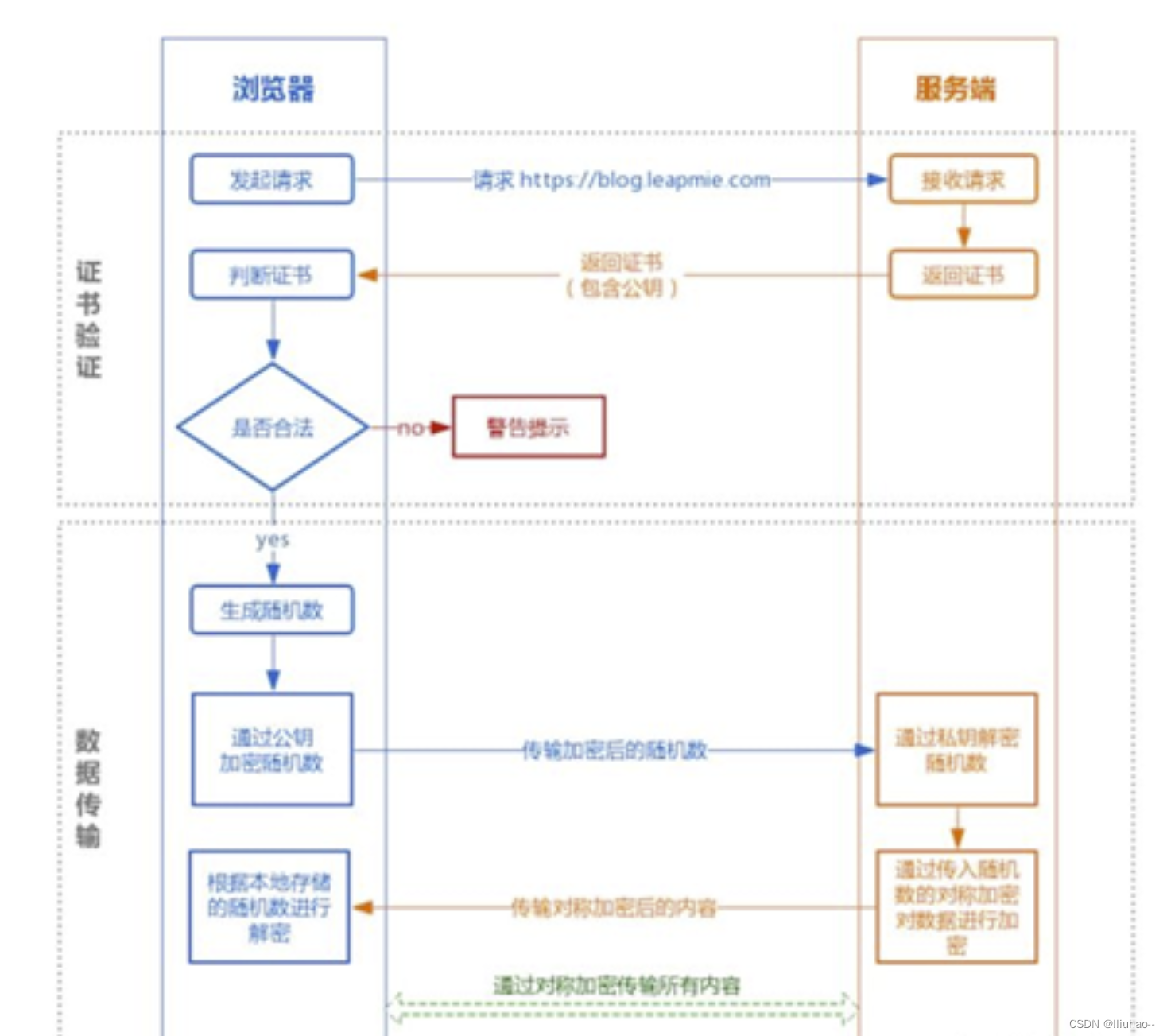
HTTPS安全套接字层超文本传输协议
HTTPS安全套接字层超文本传输协议 HTTPS简介HTTPS和HTTP的主要区别客户端在使用HTTPS方式与Web服务器通信时的步骤SSL/TLS协议的加密(握手)过程为什么数据传输阶段使用对称加密HTTPS 的优点HTTPS 的缺点HTTPS 的优化证书优化会话复用 HTTPS简介 HTTP协议…...

Jenkins发送的邮箱中没有带配置的压缩附件
【问题描述】:Jenkins中明明配置了邮箱发送时要带压缩附件,收到的邮箱中却没有附件内容 【问题定位】:压缩附件没有放在Jenkins工作空间下,所以发送的邮件并未发送附件 【解决办法】: 1)把压缩附件放到J…...

VU3-02
1.一些小点 1.1 npm i -D less (安装less) -D 安装依赖到开发环境中 只在开发中生效 正式打包的时候没有它,只在开发时有效 1.2 父子组件传参 (1)子组件中定义自己的参数和事件 父传子:const props defineProps(["item&quo…...
Linux新手小程序——进度条
前言 目录 前言 需要先了解 1.\r和\n 2.缓冲区 一.理解字符的含义: 学习c语言时,我们可以粗略把字符分为可显字符和控制字符. 在按回车换到下一行开始的操作时,实际上是进行了两个操作:1.让光标跳到下一行(只…...
会点C++还需要再学Python吗?
提到的C、数据结构与算法、操作系统、计算机网络和数据库技术等确实是计算机科学中非常重要的基础知识领域,对于软件开发和计算机工程师来说,它们是必备的核心知识。掌握这些知识对于开发高性能、可靠和安全的应用程序非常重要。Python作为一种脚本语言&…...
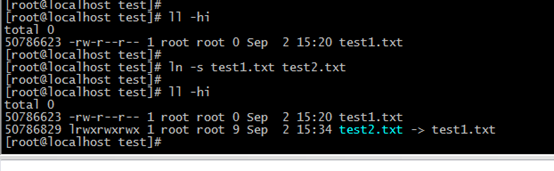
Ceph入门到精通- Linux 磁盘管理(block 与 inode)
1 硬盘 block 与 inode 详解 1.1 Sector(扇区)与 Block(块) 1) 硬盘的最小存储单位:sector(扇区),每个扇区储存 512 字节;操作系统会一次性连续读取多个…...

安全DNS,状态码,编码笔记整理
一 DNS DNS(Domain Name System)是互联网中用于将域名转换为IP地址的系统。 DNS的主要功能包括以下几个方面: 域名解析:DNS最主要的功能是将用户输入的域名解析为对应的IP地址。当用户在浏览器中输入一个域名时,操作…...
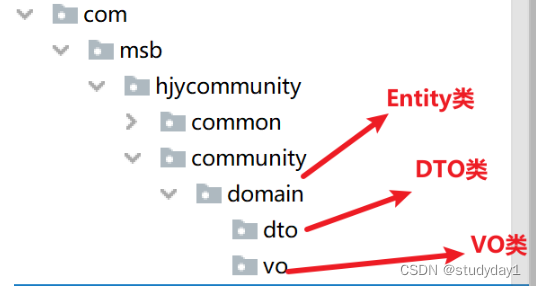
【业务功能篇53】Springboot 数据封装对象
Entity、VO、DTO解释 1)Entity:实体,与数据库的每一行数据打交道的,它的属性对应数据库每个字段 class User{ private Long idCard; private String name; private Date birthday; ...... } 对应数据库的id,name&…...

将Spring Session存储到Redis中实现持久化
文章目录 Session持久化1. 添加依赖2. 配置redis连接信息3. 存储和读取session从Redis Session持久化 1. 添加依赖 在项目中添加session依赖和redis依赖,如下所示: <dependency><groupId>org.springframework.boot</groupId><art…...

Git工作中常用命令
模拟一个git完整命令流程 有一个名为 example.txt 的文本文件 Hello, this is some text.1、做一些修改并查看文件的差异: # 修改 example.txt 文件 echo "Hello, this is some updated text." > example.txt查看文件的差异 git diffgit diff 命令…...
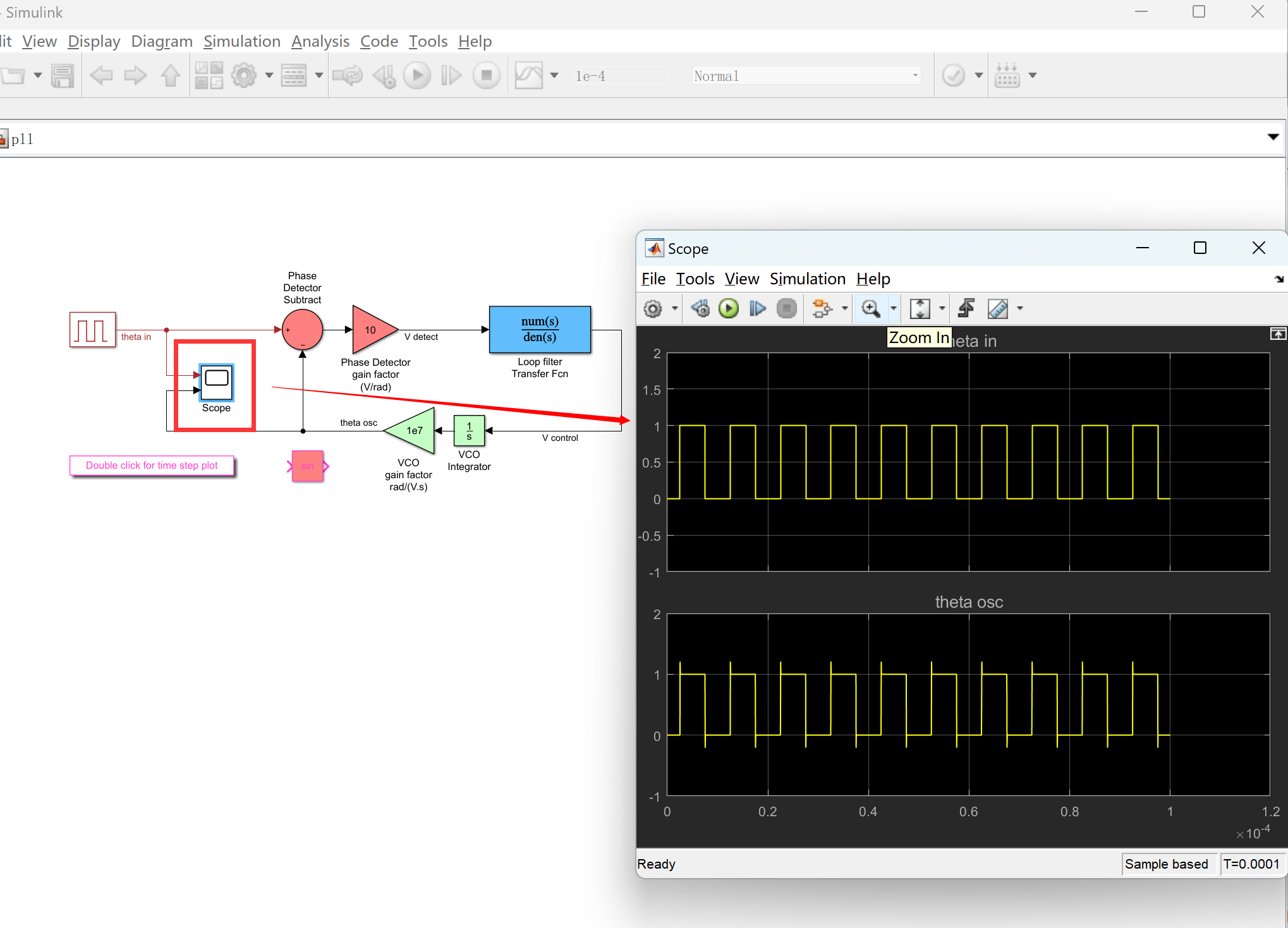
【电路效应】信号处理和通信系统模型中的模拟电路效应研究(SimulinkMatlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、Simulink仿真实现 💥1 概述 在信号处理和通信系统模型中,模拟电路效应研究是指考虑到实际电路的特性对信号进行建模和分析的过程。模拟电路效应…...

Spring 的元注解
一、元注解介绍 1.1.源码引入 1.2.元注解介绍 从上面的图片可知,Spring 有四个【负责注解其他注解】的元注解,分别是: Target:标识该注解可以用于标注哪些程序元素,比如类、方法、字段等。 Retention:标…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
