Git工作中常用命令
模拟一个git完整命令流程
有一个名为 example.txt 的文本文件
Hello, this is some text.
1、做一些修改并查看文件的差异:
# 修改 example.txt 文件
echo "Hello, this is some updated text." > example.txt
查看文件的差异
git diff
git diff 命令将显示你修改的内容,类似于:
diff --git a/example.txt b/example.txt
index 08f1df5..82ea587 100644
--- a/example.txt
+++ b/example.txt
@@ -1 +1 @@
-Hello, this is some text.
+Hello, this is some updated text.
2、暂存修改并再次查看差异
暂存修改单个文件
git add example.txt`暂存修改全部文件命令
git add ./
查看暂存区与最新提交(HEAD)之间的差异
# 查看暂存区与最新提交(HEAD)之间的差异
git diff --staged
显示如下内容:
diff --git a/example.txt b/example.txt
index 08f1df5..82ea587 100644
--- a/example.txt
+++ b/example.txt
@@ -1 +1 @@
-Hello, this is some text.
+Hello, this is some updated text.
3、提交修改并查看提交历史
# 提交修改
git commit -m "Update example.txt with new text"# 查看提交历史
git log --oneline
显示
cfc3e85 (HEAD -> main) Update example.txt with new text
6d68a12 Initial commit
4、git revert 撤回提交
使用 git revert 撤销最新的提交,需要vi编辑撤回的注释
# 使用 git revert 撤销最新的提交
git revert HEAD# 确认撤销后的提交信息,按 i 进入编辑模式,输入撤销提交的注释信息,然后按 Esc,输入 :wq 保存退出。
Git 将创建一个新的提交,该提交会撤销之前的提交。你可以在 git revert 后编辑提交信息,如果不需要更改,默认会使用撤销提交的注释信息。
查看撤销提交后的提交历史和文件内容:
# 查看提交历史
git log --oneline
显示:
81c40b1 (HEAD -> main) Revert "Update example.txt with new text"
cfc3e85 Update example.txt with new text
6d68a12 Initial commit
查看文件
# 查看 example.txt 文件内容
cat example.txt
显示文件已经撤回
Hello, this is some text.
还可以使用 git reset 命令进行撤回,详情介绍在5
5、commit后不需要撤回,直接push
Git push
如果要撤回push的代码
撤销上次提交
git revert HEAD
撤回指定的hash)
git revert e3fa6b3
撤销后,需要重新git push
# 查看提交历史
git log --oneline
查看提交历史,可以看到撤回的记录
6、git reset 撤回销命令
git reset 是不会保留提交历史记录的,git revert是有完整记录的
1、保留修改内容在暂存区
回退到哪个hash
git reset --soft hash值
在 git reset --soft 模式下,
执行 git reset --soft HEAD^
可以撤销上一个 commit,并保留修改内容在暂存区(staging area)。
这意味着之前的 commit 中的修改将回到暂存区,你可以修改这些代码并重新提交,将修改后的代码作为一个新的 commit 提交
2、不保留修改内容在暂存区(git reset 或 git reset --mixed)
在 git reset 或 git reset --mixed 模式下,
执行 git reset HEAD^ 或者简写成 git reset HEAD~1,
可以撤销上一个 commit,并将更改内容退回到工作目录(working directory),不保留在暂存区。这意味着之前的 commit 中的修改将回到工作目录,并不在暂存区,你可以对代码进行修改,并重新选择要暂存的更改,然后使用 git add 将更改添加到暂存区,再次进行 commit。
选择建议:
如果你需要撤销已经推送到远程仓库的提交,并且希望保持仓库的一致性,应该使用 git revert。
如果你需要撤销未推送的提交或者回退到之前的状态,并且明确了操作的影响,可以使用 git reset。
但请注意,git reset 可能会修改历史记录,所以要谨慎操作。
7、git merge
如果确保没有冲突,可以直接使用该命令merge最新代码到对应分支
**注意:**如果有冲突或冲突过多,建议使用可视化文件对比idea工具,进行merge,并在可视化文件对比中进行冲突的解决。
相关文章:

Git工作中常用命令
模拟一个git完整命令流程 有一个名为 example.txt 的文本文件 Hello, this is some text.1、做一些修改并查看文件的差异: # 修改 example.txt 文件 echo "Hello, this is some updated text." > example.txt查看文件的差异 git diffgit diff 命令…...
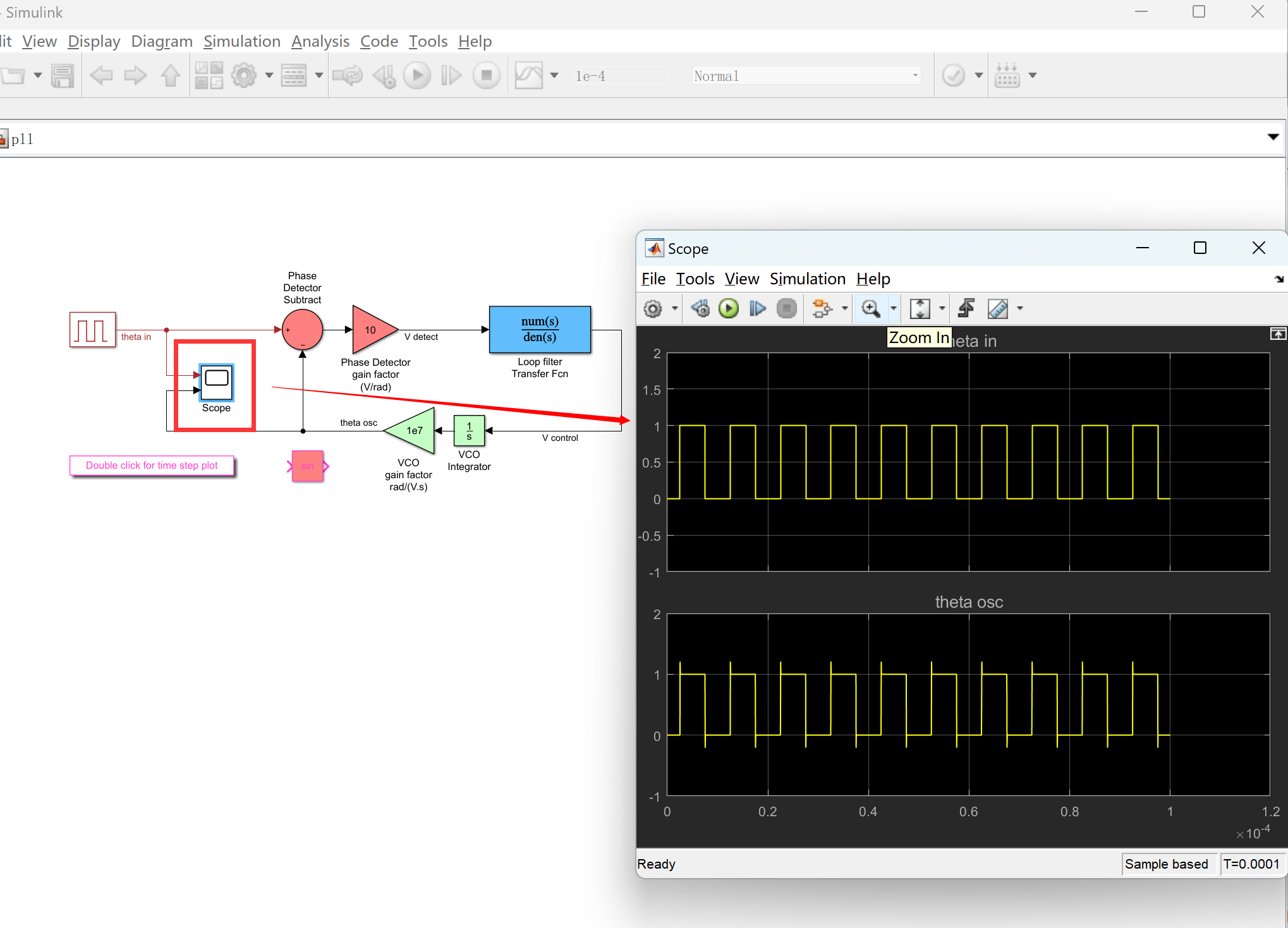
【电路效应】信号处理和通信系统模型中的模拟电路效应研究(SimulinkMatlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、Simulink仿真实现 💥1 概述 在信号处理和通信系统模型中,模拟电路效应研究是指考虑到实际电路的特性对信号进行建模和分析的过程。模拟电路效应…...

Spring 的元注解
一、元注解介绍 1.1.源码引入 1.2.元注解介绍 从上面的图片可知,Spring 有四个【负责注解其他注解】的元注解,分别是: Target:标识该注解可以用于标注哪些程序元素,比如类、方法、字段等。 Retention:标…...

【前缀和】238. 除自身以外数组的乘积
238. 除自身以外数组的乘积 解题思路 前缀与后缀的思路对于给定索引i,将它左边的所有数字乘积乘以右边所有数字的乘积初始化两个数组L R计算L[i] L[i - 1] * nums[i - 1] 也就是左侧所有数字的乘积计算R[i] R[i 1] * nums[i 1] 也就是右侧所有数字的成绩计算L…...
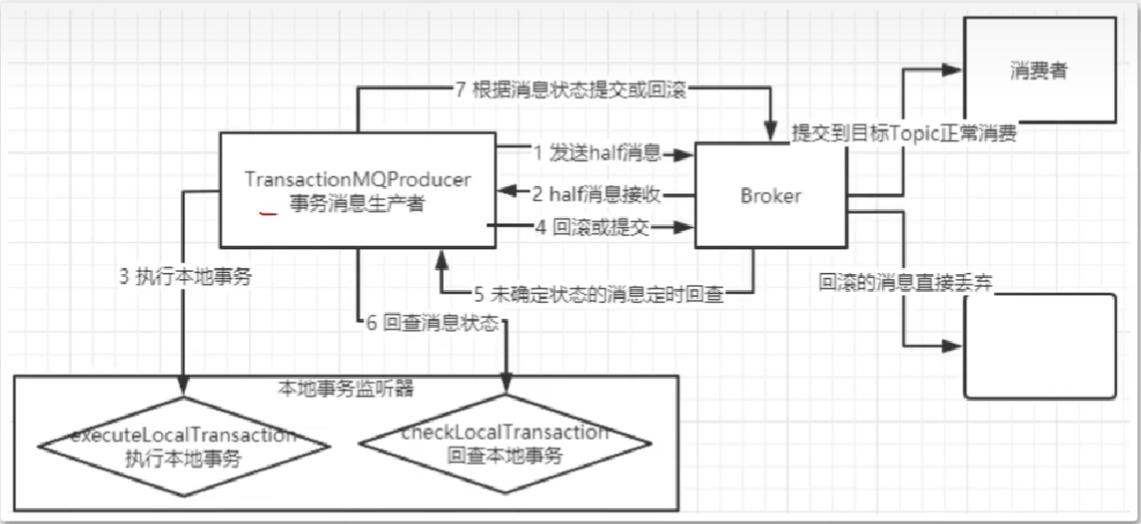
【Java中间件】RocketMQ
RocketMQ 一、MQ概述 Message Queue,是一种提供消息队列服务的中间件。提供了消息生产、存储、消费全过程API的软件系统。 MQ的作用 限流削峰:当用户发送超量请求时,将请求暂存,以便后期慢慢处理。如果不使用MQ暂存直接请求到…...
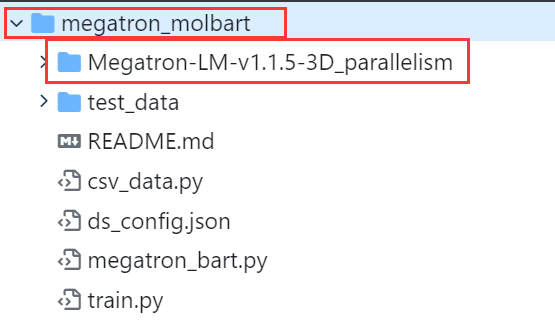
Megatron-LM、NVIDIA NeMo、MegaMolBART 、model_optim_rng.pt 文件是什么?
本文涉及以下几个概念,分别是: Megatron和Megatron-LM-v1.1.5-3D_parallelism NVIDIA NeMo Megatron和Megatron-LM-v1.1.5-3D_parallelism是什么? Megatron是由NVIDIA开发的一种用于训练大规模语言模型的开源框架。它旨在提供高效的分布式…...

2023年信息系统项目管理师如何报名?老司机告诉你
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...

linux ubuntu系统 命令备忘
一、安装软件包的命令 1、验证安装包是否安装 dpkg -s <软件包名> 2、从软件源服务器获取最新的软件信息并缓存到本地 apt update 3、从本地仓库中对比系统中所有已安装的软件,如果有新版本的话则进行升级 apt upgrade 4、列出本地仓库中所有的软件包名…...
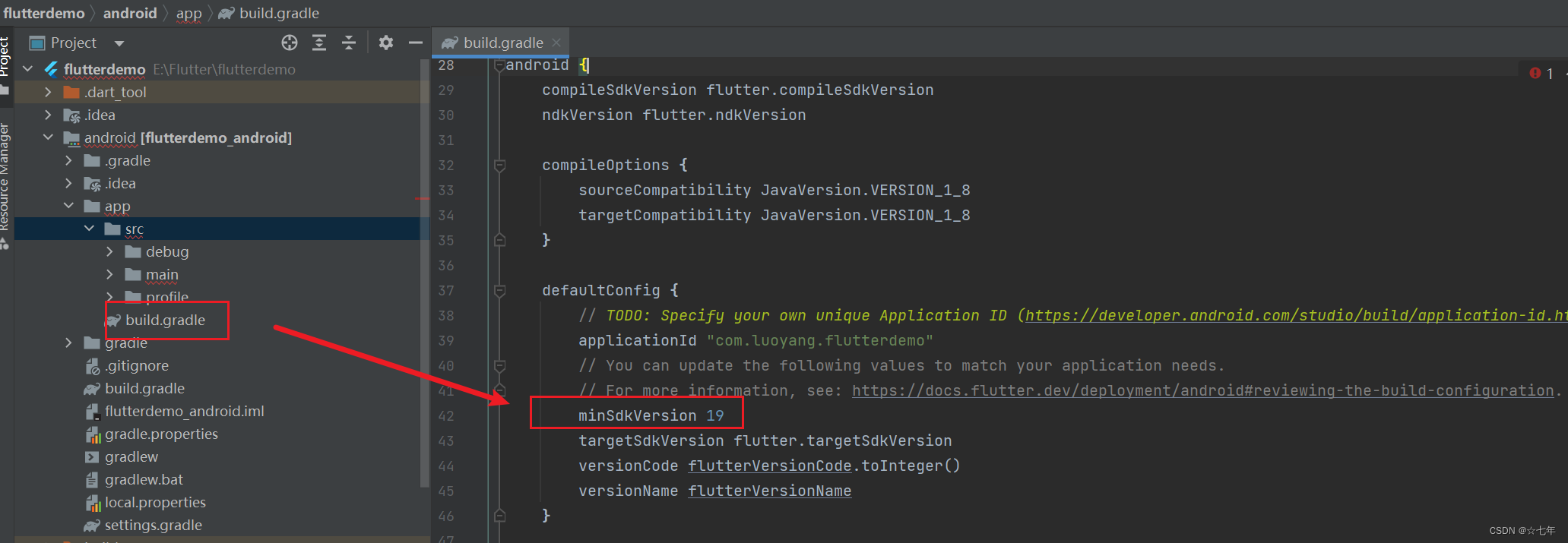
我的第一个flutter项目(Android Webview)
前言:flutter开发环境搭建Flutter的开发环境搭建-图解_☆七年的博客-CSDN博客 第一个flutter简单项目,内容是一个主界面,其中: 1.内容点击数字自增 2.跳转一个空页, 3.跳转一个WebView界面 其中涉及添加主键…...

微信机器人搭建详细教程
确保已安装Python和pip。 在D盘上创建名为wxbot的文件夹,并将你的Python机器人项目文件放在这个目录中。 在D盘的wxbot文件夹中打开命令行工具,并创建一个新的Python虚拟环境(可选): python -m venv venv激活虚拟环…...

opengauss安装
opengauss安装 系统环境 Redhat版本:redhat7.6 虚拟机ip:192.168.5.144 Gauss版本:openGauss-5.0.0-CentOS-64bit-all.tar.gz 企业版 一.准备软硬件环境 1.1 安装依赖包 yum -y install bzip2 python3 libaio-devel flex bis…...
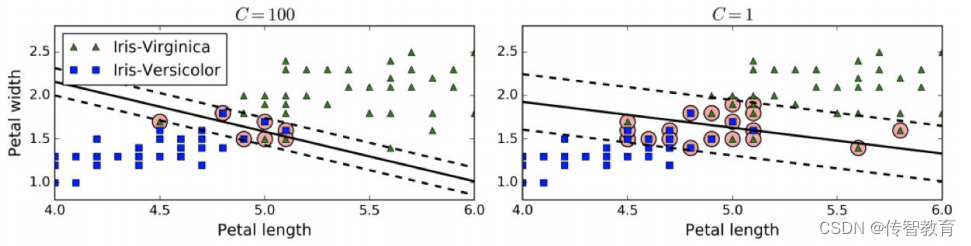
什么是SVM算法?硬间隔和软间隔的分类问题
SVM全称是supported vector machine(支持向量机),即寻找到一个超平面使样本分成两类,并且间隔最大。 SVM能够执行线性或⾮线性分类、回归,甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一。SVM特别适用于中小型复杂数据集的分类。…...

Normalization(BN and LN) in NN
Batch Normalization 称为批标准化。批是指一批数据,通常为 mini-batch;标准化是处理后的数据服从 N ( 0 , 1 ) N(0,1) N(0,1) 的正态分布。在训练过程中,数据需要经过多层的网络,如果数据在前向传播的过程中,尺度发…...
opencv-22 图像几何变换01-缩放-cv2.resize()(图像增强,图像变形,图像拼接)
什么是几何变换? 几何变换是计算机图形学中的一种图像处理技术,用于对图像进行空间上的变换,而不改变图像的内容。这些变换可以通过对图像中的像素位置进行调整来实现。 常见的几何变换包括: 平移(Translation&#x…...

python机器学习(五)逻辑回归、决策边界、代价函数、梯度下降法实现线性和非线性逻辑回归
线性回归所解决的问题是把数据集的特征传入到模型中,预测一个值使得误差最小,预测值无限接近于真实值。比如把房子的其他特征传入到模型中,预测出房价, 房价是一系列连续的数值,线性回归解决的是有监督的学习。有很多场…...
, AsQueryable() ,.ToList(),的区别和用法)
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法
聊聊Linq中.AsEnumerable(), AsQueryable() ,.ToList(),的区别和用法 当使用LINQ查询数据时,我们常常会面临选择使用.AsEnumerable(), .AsQueryable(), 和 .ToList()方法的情况。这些方法在使用时有不同的效果和影响,需要根据具体场景来选择合适的方法。…...

【机器学习】机器学习中的“本体”概念
一、说明 在机器学习中,本体越来越多地用于提供基于相似性分析和场景知识的 ML 模型。 在传统的基于标签的定义中,对象往往是孤立的,可扩展性差,存在重复的可能性,对象之间的关系无法体现。在基于本体的定义中…...

ChatGPT是否能够进行对话中的参考和指代解析?
ChatGPT在对话中的参考和指代解析方面有一定的潜力,但需要针对具体任务和上下文进行定制和优化。参考和指代解析是指理解对话中的代词、名词短语等表达方式所指代的具体对象或信息。在对话中,参考和指代解析对于理解上下文、保持对话连贯性和生成准确回复…...
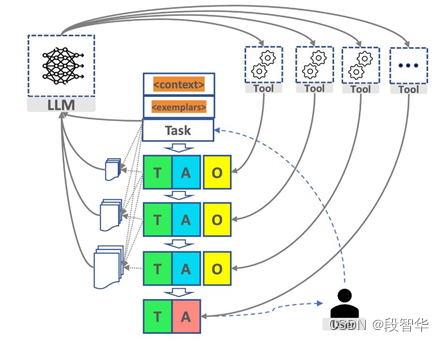
网红项目AutoGPT源码内幕及综合案例实战(三)
AutoGPT on LangChain PromptGenerator等源码解析 本节阅读AutoGPT 的prompt_generator.py源代码,其中定义了一个PromptGenerator类和一个get_prompt函数,用于生成一个提示词信息。PromptGenerator类提供了添加约束、命令、资源和性能评估等内容的方法,_generate_numbered_l…...

第八章:list类
系列文章目录 文章目录 系列文章目录前言list的介绍及使用list的介绍list的使用list的构造函数list的迭代器list的容量list的成员访问list的增删改查 list与vector的对比总结 前言 list是STL的一种链表类,可以在常数范围内在任意位置进行插入和删除的序列式容器。 …...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
