会点C++还需要再学Python吗?
提到的C++、数据结构与算法、操作系统、计算机网络和数据库技术等确实是计算机科学中非常重要的基础知识领域,对于软件开发和计算机工程师来说,它们是必备的核心知识。掌握这些知识对于开发高性能、可靠和安全的应用程序非常重要。
Python作为一种脚本语言,在某些场景下确实可以作为加分项或辅助工具使用。它具有易学易用的特点,并且在数据处理、科学计算、机器学习等领域具有广泛的应用。对于一些快速原型开发、数据分析和自动化脚本等任务,Python可以提高开发效率。
然而,选择学习哪些技术和语言取决于你的个人兴趣、职业目标和所在行业的需求。如果你对C++后台开发感兴趣,并且想在该领域深入发展,那么深入学习C++、数据结构与算法、操作系统等是很重要的。同时,也要根据具体岗位要求和行业趋势来补充其他相关技术,如计算机网络和数据库技术。
面试准备确实需要通过了解面试问题、面试经验和实际工作经验来提升自己的技能。每个人的情况和面试要求都有所不同,因此需要根据自己的实际情况进行有针对性的准备。刚好,我这里有上位机入门,学习线路图,各种项目,需要留个6。不断学习和提升自己的技能,扩展自己的知识广度和深度,对于在面试和工作中更好地展示自己的能力是非常重要的。
相关文章:

会点C++还需要再学Python吗?
提到的C、数据结构与算法、操作系统、计算机网络和数据库技术等确实是计算机科学中非常重要的基础知识领域,对于软件开发和计算机工程师来说,它们是必备的核心知识。掌握这些知识对于开发高性能、可靠和安全的应用程序非常重要。Python作为一种脚本语言&…...
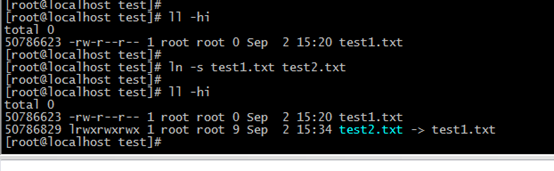
Ceph入门到精通- Linux 磁盘管理(block 与 inode)
1 硬盘 block 与 inode 详解 1.1 Sector(扇区)与 Block(块) 1) 硬盘的最小存储单位:sector(扇区),每个扇区储存 512 字节;操作系统会一次性连续读取多个…...

安全DNS,状态码,编码笔记整理
一 DNS DNS(Domain Name System)是互联网中用于将域名转换为IP地址的系统。 DNS的主要功能包括以下几个方面: 域名解析:DNS最主要的功能是将用户输入的域名解析为对应的IP地址。当用户在浏览器中输入一个域名时,操作…...
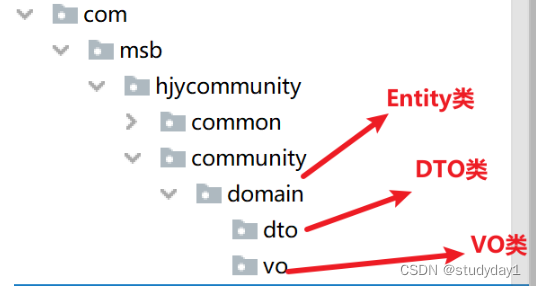
【业务功能篇53】Springboot 数据封装对象
Entity、VO、DTO解释 1)Entity:实体,与数据库的每一行数据打交道的,它的属性对应数据库每个字段 class User{ private Long idCard; private String name; private Date birthday; ...... } 对应数据库的id,name&…...

将Spring Session存储到Redis中实现持久化
文章目录 Session持久化1. 添加依赖2. 配置redis连接信息3. 存储和读取session从Redis Session持久化 1. 添加依赖 在项目中添加session依赖和redis依赖,如下所示: <dependency><groupId>org.springframework.boot</groupId><art…...

Git工作中常用命令
模拟一个git完整命令流程 有一个名为 example.txt 的文本文件 Hello, this is some text.1、做一些修改并查看文件的差异: # 修改 example.txt 文件 echo "Hello, this is some updated text." > example.txt查看文件的差异 git diffgit diff 命令…...
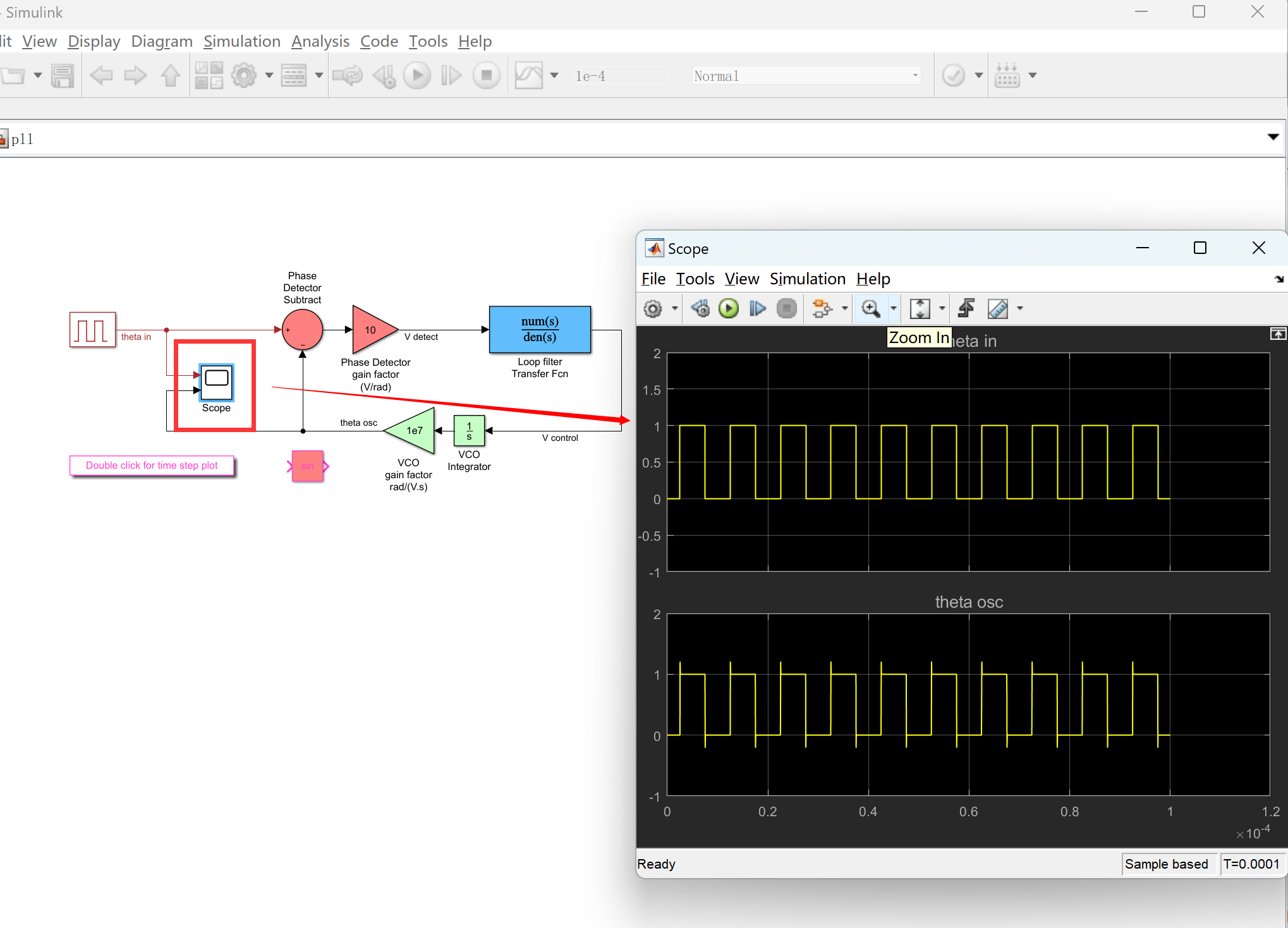
【电路效应】信号处理和通信系统模型中的模拟电路效应研究(SimulinkMatlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码、Simulink仿真实现 💥1 概述 在信号处理和通信系统模型中,模拟电路效应研究是指考虑到实际电路的特性对信号进行建模和分析的过程。模拟电路效应…...

Spring 的元注解
一、元注解介绍 1.1.源码引入 1.2.元注解介绍 从上面的图片可知,Spring 有四个【负责注解其他注解】的元注解,分别是: Target:标识该注解可以用于标注哪些程序元素,比如类、方法、字段等。 Retention:标…...

【前缀和】238. 除自身以外数组的乘积
238. 除自身以外数组的乘积 解题思路 前缀与后缀的思路对于给定索引i,将它左边的所有数字乘积乘以右边所有数字的乘积初始化两个数组L R计算L[i] L[i - 1] * nums[i - 1] 也就是左侧所有数字的乘积计算R[i] R[i 1] * nums[i 1] 也就是右侧所有数字的成绩计算L…...
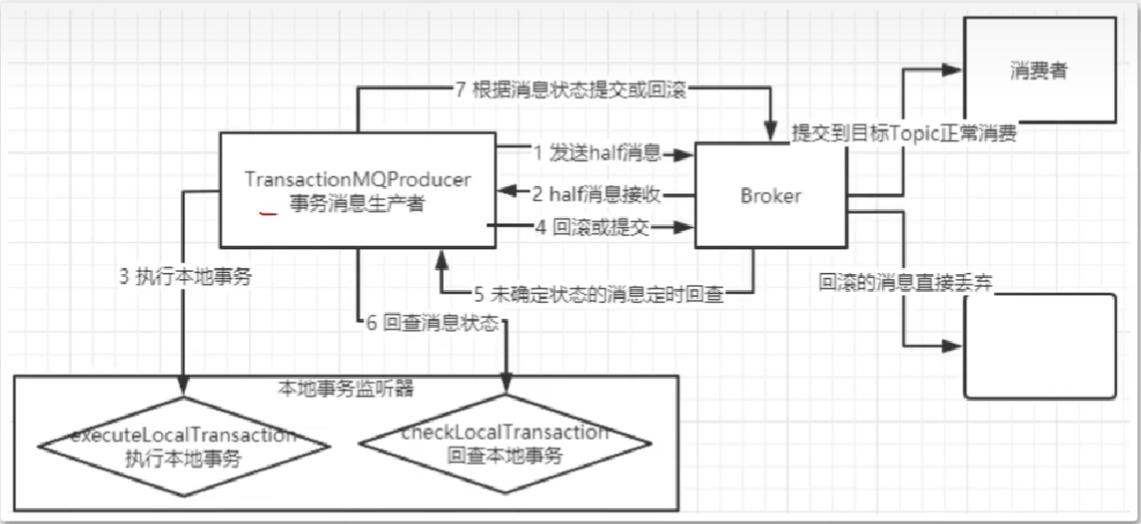
【Java中间件】RocketMQ
RocketMQ 一、MQ概述 Message Queue,是一种提供消息队列服务的中间件。提供了消息生产、存储、消费全过程API的软件系统。 MQ的作用 限流削峰:当用户发送超量请求时,将请求暂存,以便后期慢慢处理。如果不使用MQ暂存直接请求到…...
Megatron-LM、NVIDIA NeMo、MegaMolBART 、model_optim_rng.pt 文件是什么?
本文涉及以下几个概念,分别是: Megatron和Megatron-LM-v1.1.5-3D_parallelism NVIDIA NeMo Megatron和Megatron-LM-v1.1.5-3D_parallelism是什么? Megatron是由NVIDIA开发的一种用于训练大规模语言模型的开源框架。它旨在提供高效的分布式…...

2023年信息系统项目管理师如何报名?老司机告诉你
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...

linux ubuntu系统 命令备忘
一、安装软件包的命令 1、验证安装包是否安装 dpkg -s <软件包名> 2、从软件源服务器获取最新的软件信息并缓存到本地 apt update 3、从本地仓库中对比系统中所有已安装的软件,如果有新版本的话则进行升级 apt upgrade 4、列出本地仓库中所有的软件包名…...
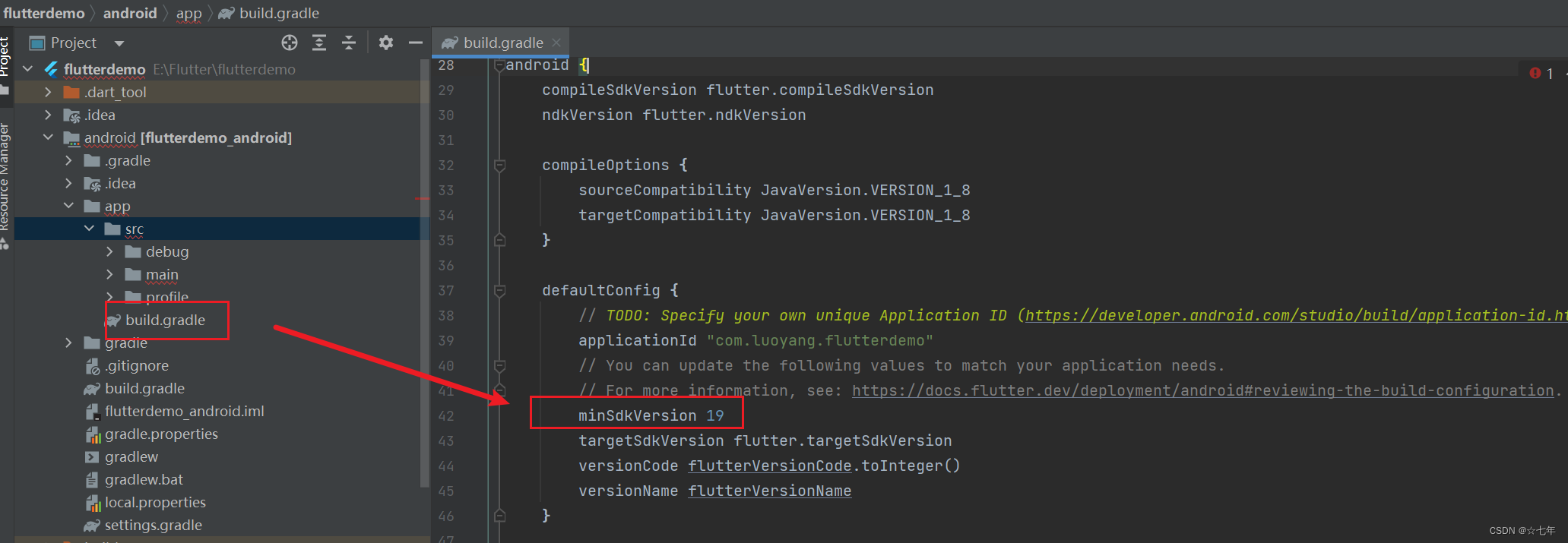
我的第一个flutter项目(Android Webview)
前言:flutter开发环境搭建Flutter的开发环境搭建-图解_☆七年的博客-CSDN博客 第一个flutter简单项目,内容是一个主界面,其中: 1.内容点击数字自增 2.跳转一个空页, 3.跳转一个WebView界面 其中涉及添加主键…...

微信机器人搭建详细教程
确保已安装Python和pip。 在D盘上创建名为wxbot的文件夹,并将你的Python机器人项目文件放在这个目录中。 在D盘的wxbot文件夹中打开命令行工具,并创建一个新的Python虚拟环境(可选): python -m venv venv激活虚拟环…...

opengauss安装
opengauss安装 系统环境 Redhat版本:redhat7.6 虚拟机ip:192.168.5.144 Gauss版本:openGauss-5.0.0-CentOS-64bit-all.tar.gz 企业版 一.准备软硬件环境 1.1 安装依赖包 yum -y install bzip2 python3 libaio-devel flex bis…...
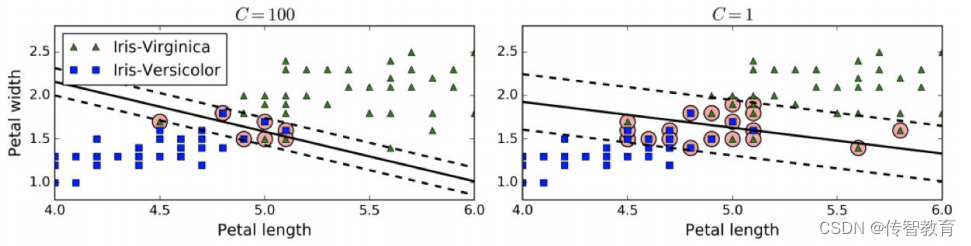
什么是SVM算法?硬间隔和软间隔的分类问题
SVM全称是supported vector machine(支持向量机),即寻找到一个超平面使样本分成两类,并且间隔最大。 SVM能够执行线性或⾮线性分类、回归,甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一。SVM特别适用于中小型复杂数据集的分类。…...

Normalization(BN and LN) in NN
Batch Normalization 称为批标准化。批是指一批数据,通常为 mini-batch;标准化是处理后的数据服从 N ( 0 , 1 ) N(0,1) N(0,1) 的正态分布。在训练过程中,数据需要经过多层的网络,如果数据在前向传播的过程中,尺度发…...
opencv-22 图像几何变换01-缩放-cv2.resize()(图像增强,图像变形,图像拼接)
什么是几何变换? 几何变换是计算机图形学中的一种图像处理技术,用于对图像进行空间上的变换,而不改变图像的内容。这些变换可以通过对图像中的像素位置进行调整来实现。 常见的几何变换包括: 平移(Translation&#x…...

python机器学习(五)逻辑回归、决策边界、代价函数、梯度下降法实现线性和非线性逻辑回归
线性回归所解决的问题是把数据集的特征传入到模型中,预测一个值使得误差最小,预测值无限接近于真实值。比如把房子的其他特征传入到模型中,预测出房价, 房价是一系列连续的数值,线性回归解决的是有监督的学习。有很多场…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
