VAE-根据李宏毅视频总结的最通俗理解
1.VAE的直观理解
先简单了解一下自编码器,也就是常说的Auto-Encoder。Auto-Encoder包括一个编码器(Encoder)和一个解码器(Decoder)。其结构如下:

自编码器是一种先把输入数据压缩为某种编码, 后仅通过该编码重构出原始输入的结构. 从描述来看, AE是一种无监督方法.
AE的结构非常明确, 需要有一个压缩编码的Encoder和就一个相应解码重构的Decoder
那么VAE的目标是什么?为什么VAE呢?
-------VAE作为一个生成模型,其基本思路是很容易理解的:把一堆真实样本通过编码器网络变换成一个理想的数据分布,然后这个数据分布再传递给一个解码器网络,得到一堆生成样本,生成样本与真实样本足够接近的话,就训练出了一个自编码器模型。
为什么要用VAE,原来的Auto Encoder有什么问题呢?那面下面是一个直观的解释。
下图是 AutoEncoder 的简单例子:我们把一张满月的图片 Encoder 后得到 code,这个code被decoder 后又转换为满月图,弦月图也是如此。注意它们直接的一对一关系。图片左边那个问号的意思是当对 AE 中的code进行随机采样时,它介于满月与弦月之间的数据,decoder后可能会输出什么?
-------------可能会输出满月,可能会输出弦月,但是最有可能输出的是奇奇怪怪的图片。
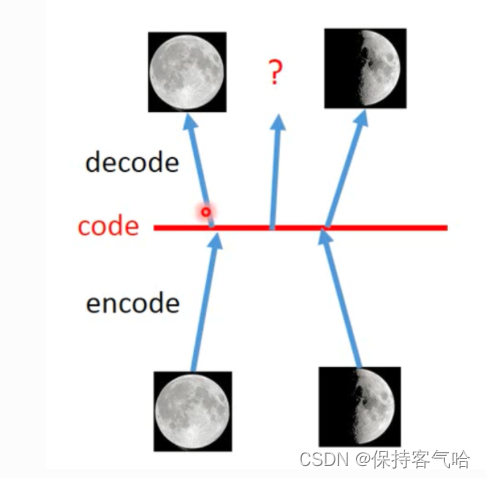
下图是 VAE 的简单例子,我们在 code 中添加一些 noise,这样可以让在满月对应 noise 范围内的code 都可以转换为满月,弦月对应的noise 范围内的code也能转换成弦月。但当我们在不是满月和弦月对应的noise的code中采样时,decoder出来的图片可能是介于满月和弦月之间的图。也就是说,VAE 产生了输入数据中不包含的数据,(可以认为产生了含有某种特定信息的新的数据),而 AE 只能产生尽可能接近或者就是以前的数据(当数据简单时,编码解码损耗少时)。
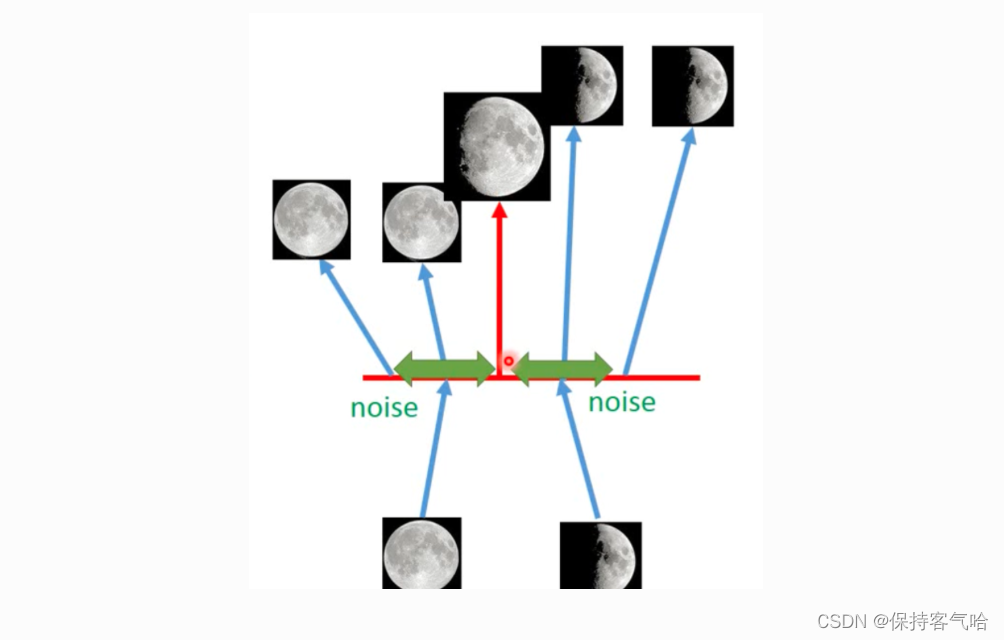
2.VAE的模型直观展示
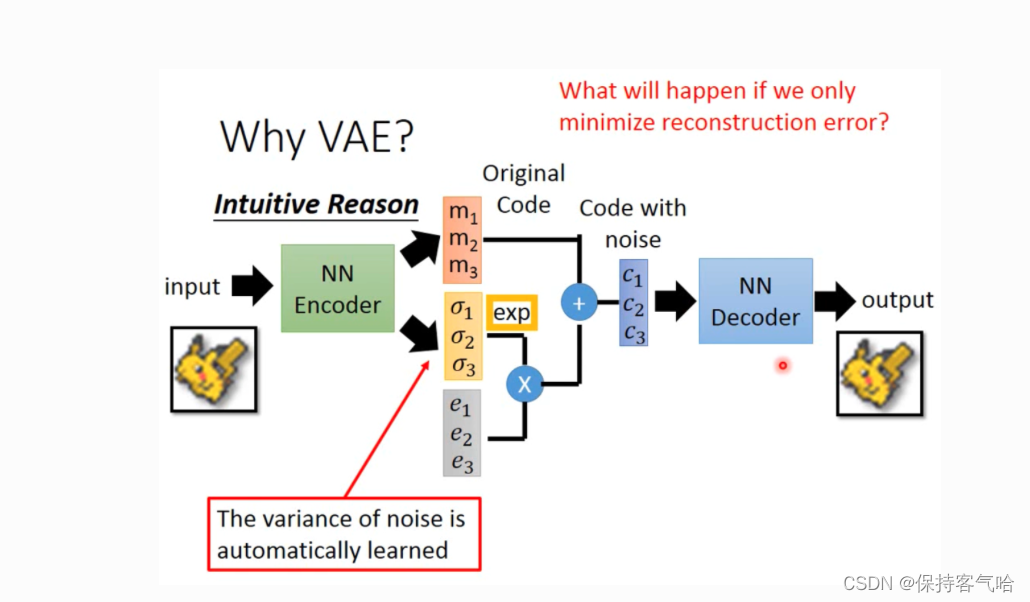
在VAE中,为了给编码添加合适的噪音,编码器会输出两个编码,一个是原有编码 m 1 , m 2 , m 3 m_1,m_2,m_3 m1,m2,m3,另外一个是控制噪音干扰程度的编码 σ 1 , σ 2 , σ 3 \sigma_1,\sigma_2,\sigma_3 σ1,σ2,σ3,第二个编码其实很好理解,就是为随机噪音码 e 1 , e 2 , e 3 e_1,e_2,e_3 e1,e2,e3分配权重,然后加上exp的目的是为了保证这个分配的权重是个正值,最后将原编码与噪音编码相加,就得到了VAE在code层的输出结果 c 1 , c 2 , c 3 c_1,c_2,c_3 c1,c2,c3。
损失函数方面,除了必要的重构损失外,VAE还增添了一个损失函数,这同样是必要的部分,因为如果不加的话,整个模型就会出现问题:为了保证生成图片的质量越高,编码器肯定希望噪音对自身生成图片的干扰越小,于是分配给噪音的权重越小,这样只需要将 σ 1 , σ 2 , σ 3 \sigma_1,\sigma_2,\sigma_3 σ1,σ2,σ3赋为接近负无穷大的值就好了。所以,第二个损失函数就有限制编码器走这样极端路径的作用,这也从直观上就能看出来, e x p ( σ i ) − ( 1 + σ i ) exp(\sigma_i)-(1+\sigma_i) exp(σi)−(1+σi)在x=0处取得最小值,于是 σ 1 , σ 2 , σ 3 \sigma_1,\sigma_2,\sigma_3 σ1,σ2,σ3就会避免被赋值为负无穷大。
3.VAE的基本原理
那先回到我们到底想做什么?我们现在是想要生成图片,就拿下图距离,每张图片可以看做高维空间的一个点,然后这些图片符合一个分布P(x),我们要做的事情就是去预测这个高维空间的概率分布P(x),只要我们知道这个分布我们就可以从中sample然后得到图片。
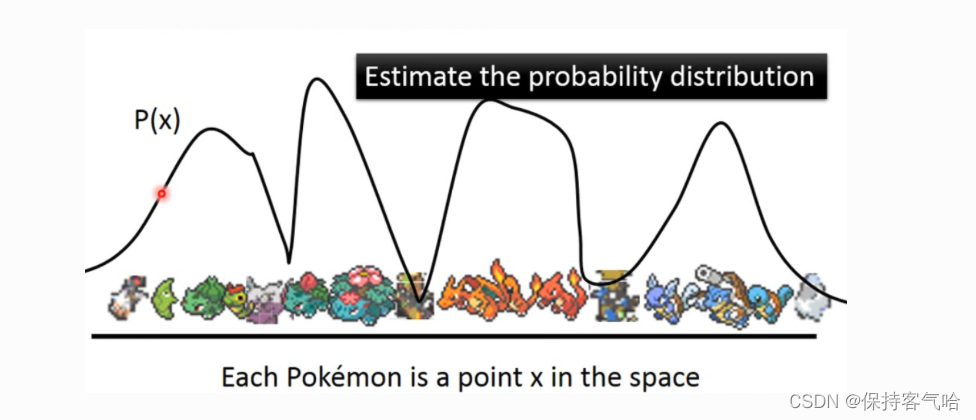
那如何去知道这个分布呢?我们先了解一下什么是高斯混合模型?------------即任何一个数据的分布,都可以看作是若干高斯分布的叠加。
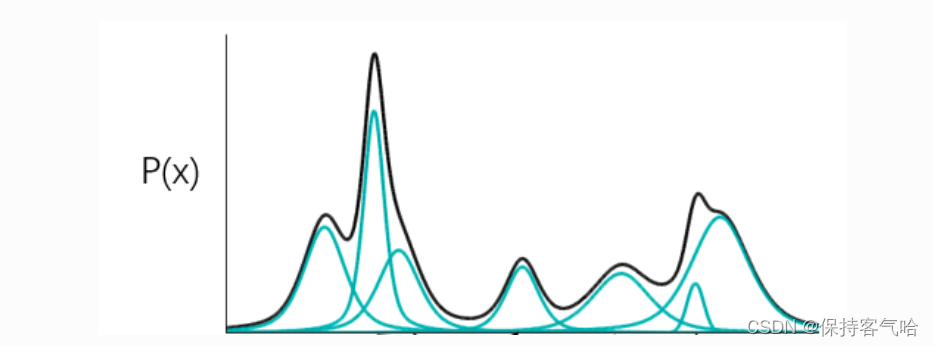
上图中黑色代表的是P(x)分布,蓝色的线都是不同的高斯分布,我们可以用若干个高斯分布去拟合P(x),那如果我们想要从P(x)去sample一个东西,那我们就要去考虑我们是从哪个高斯分布中去sample。然后这个这个过程可以表示为下图

其中最下面的代表的是高斯分布,m代表的是第几个高斯分布,蓝色的柱状图即P(m)代表的是去选择某一个高斯分布(m)的概率,所以P(x)可以表示为黄色标记所示,每个m对应的高斯分布有自己的均值和方差。
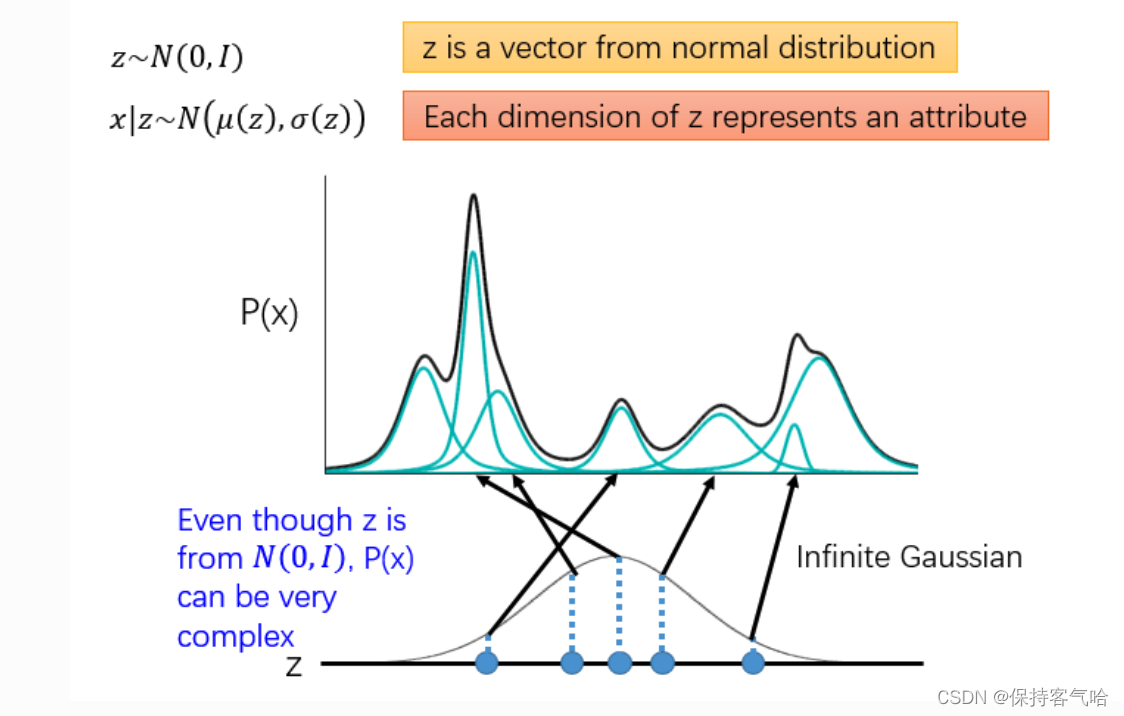
现在我们借助一个变量$ z\sim N(0,I)$ ,(注意z是一个向量,生成自一个高斯分布),找一个映射关系,将向量z映射成这一系列高斯分布的参数向量 μ ( z ) \mu (z) μ(z)和$ \sigma (z)$。有了这一系列高斯分布的参数我们就可以得到叠加后的P(x)的形式。也就是说我们只要知道每个高斯分布的参数,我们就能用它拟合P(x)
那么现在 P ( x ) = ∫ P ( z ) P ( x ∣ z ) d z ( 1 ) P(x) = ∫P(z)P(x∣z)dz \quad(1) P(x)=∫P(z)P(x∣z)dz(1) , 其中 z ∼ N ( 0 , I ) , x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) z \sim N(0,I), \quad x|z \sim N \big(\mu(z), \sigma(z)\big) z∼N(0,I),x∣z∼N(μ(z),σ(z))
接下来就可以求解这个式子。由于P(z)是已知的,P(x|z)未知,而 x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) x|z \sim N \big(\mu(z), \sigma(z)\big) x∣z∼N(μ(z),σ(z)),于是我们真正需要求解的,是 μ ( z ) \mu (z) μ(z)和$ \sigma (z)$两个函数的表达式。很难直接计算积分部分,因为我们很难穷举出所有的向量z用于计算积分,我们需要引入两个神经网络来帮助我们求解。
-
第一个神经网络在VAE叫做Decoder,它求解的 μ ( z ) \mu (z) μ(z)和$ \sigma (z)$和两个函数,这等价于求解P(x|z)。

-
第二个神经网络在VAE叫做Encoder,它求解的结果是 q ( z ∣ x ) , z ∣ x ∼ N ( μ ′ ( x ) , σ ′ ( x ) ) q(z∣x), z|x \sim N\big(\mu^\prime(x), \sigma^\prime(x)\big) q(z∣x),z∣x∼N(μ′(x),σ′(x)),q可以代表任何分布。它主要是用来得到给定一个 x 然后得到对应 z 的 μ ′ ( x ) , σ ′ ( x ) \mu^\prime(x), \sigma^\prime(x) μ′(x),σ′(x)

这儿引入第二个神经网络Encoder的目的是,辅助第一个Decoder求解P(x|z)
现在梳理一下我们的目的,我们需要求P(x),然后P(x)可以表示为:
P ( x ) = ∫ P ( z ) P ( x ∣ z ) d z P(x) = ∫P(z)P(x∣z)dz P(x)=∫P(z)P(x∣z)dz
我们希望P(x)越大越好,等价于求
M a x m i z e L = ∑ x l o g P ( x ) Maxmize L = \sum_x logP(x) MaxmizeL=x∑logP(x)
又因为
log P ( x ) = ∫ z q ( z ∣ x ) log P ( x ) d z \log P(x) = \int_z q(z|x) \log P(x) dz logP(x)=∫zq(z∣x)logP(x)dz
因为 ∫ z q ( z ∣ x ) d z = 1 \int_z q(z|x) dz = 1 ∫zq(z∣x)dz=1
所以
log P ( x ) = ∫ z q ( z ∣ x ) log P ( z , x ) P ( z ∣ x ) d z = ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) q ( z ∣ x ) P ( z ∣ x ) d z = ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) d z + ∫ z q ( z ∣ x ) log q ( z ∣ x ) P ( z ∣ x ) d z = D K L ( q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) ) + ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) d z ≥ ∫ z q ( z ∣ x ) log P ( x ∣ z ) P ( z ) q ( z ∣ x ) d z since D K L ( q ∣ ∣ P ) ≥ 0 \begin{aligned} \log P(x) &= \int_z q(z|x) \log \frac{P(z,x)}{P(z|x)} dz \\ &= \int_z q(z|x) \log \frac{P(z,x)q(z|x)}{q(z|x)P(z|x)} dz \\ &= \int_z q(z|x) \log \frac{P(z,x)}{q(z|x)} dz + \int_z q(z|x) \log \frac{q(z|x)}{P(z|x)} dz \\ &= D_{KL}(q(z|x) || P(z|x)) + \int_z q(z|x) \log \frac{P(z,x)}{q(z|x)} dz \\ &\geq \int_z q(z|x) \log \frac{P(x|z)P(z)}{q(z|x)} dz \quad \text{since } D_{KL}(q||P) \geq 0 \end{aligned} logP(x)=∫zq(z∣x)logP(z∣x)P(z,x)dz=∫zq(z∣x)logq(z∣x)P(z∣x)P(z,x)q(z∣x)dz=∫zq(z∣x)logq(z∣x)P(z,x)dz+∫zq(z∣x)logP(z∣x)q(z∣x)dz=DKL(q(z∣x)∣∣P(z∣x))+∫zq(z∣x)logq(z∣x)P(z,x)dz≥∫zq(z∣x)logq(z∣x)P(x∣z)P(z)dzsince DKL(q∣∣P)≥0
我们将 ∫ z q ( z ∣ x ) log P ( x ∣ z ) P ( z ) q ( z ∣ x ) d z \int_z q(z|x) \log \frac{P(x|z)P(z)}{q(z|x)} dz ∫zq(z∣x)logq(z∣x)P(x∣z)P(z)dz 称为 log P ( x ) \log P(x) logP(x) 的 (variational) lower bound (变分下界),简称为 L b L_b Lb。
即 原式化简为 l o g P ( x ) = L b + K L ( q ( z ∣ x ) ∣ ∣ p ( z ∣ x ) ) log P(x) = L_b + KL(q(z|x)||p(z|x)) logP(x)=Lb+KL(q(z∣x)∣∣p(z∣x))
原本,我们需要求 P ( x ∣ z ) P(x|z) P(x∣z) 使得 l o g P ( x ) log P(x) logP(x) 最大,现在引入了一个 q ( z ∣ x ) q(z|x) q(z∣x),变成了同时求 P ( x ∣ z ) P(x|z) P(x∣z)和 q ( z ∣ x ) q(z|x) q(z∣x)使得 l o g P ( x ) log P(x) logP(x)最大。实际上,因为后验分布 P ( z ∣ x ) P(z|x) P(z∣x) 很难求 (intractable),所以才用 q ( z ∣ x ) q(z|x) q(z∣x) 来逼近这个后验分布。在优化的过程中我们发现,首先 q ( z ∣ x ) q(z|x) q(z∣x) 跟 log P ( x ) \log P(x) logP(x) 是完全没有关系的, log P ( x ) \log P(x) logP(x) 只跟 P ( z ∣ x ) P(z|x) P(z∣x) 有关,调节 q ( z ∣ x ) q(z|x) q(z∣x) 是不会影响似然也就是 log P ( x ) \log P(x) logP(x) 的。所以,当我们固定住 P ( x ∣ z ) P(x|z) P(x∣z) 时,调节 q ( z ∣ x ) q(z|x) q(z∣x) 最大化下界 L b L_b Lb,KL 则越小。当 q ( z ∣ x ) q(z|x) q(z∣x) 逼近后验分布 P ( z ∣ x ) P(z|x) P(z∣x) 时,KL 散度趋于为 0, log P ( x ) \log P(x) logP(x) 就和 L b L_b Lb 等价。所以最大化 log P ( x ) \log P(x) logP(x) 就等价于最大化 L b L_b Lb。
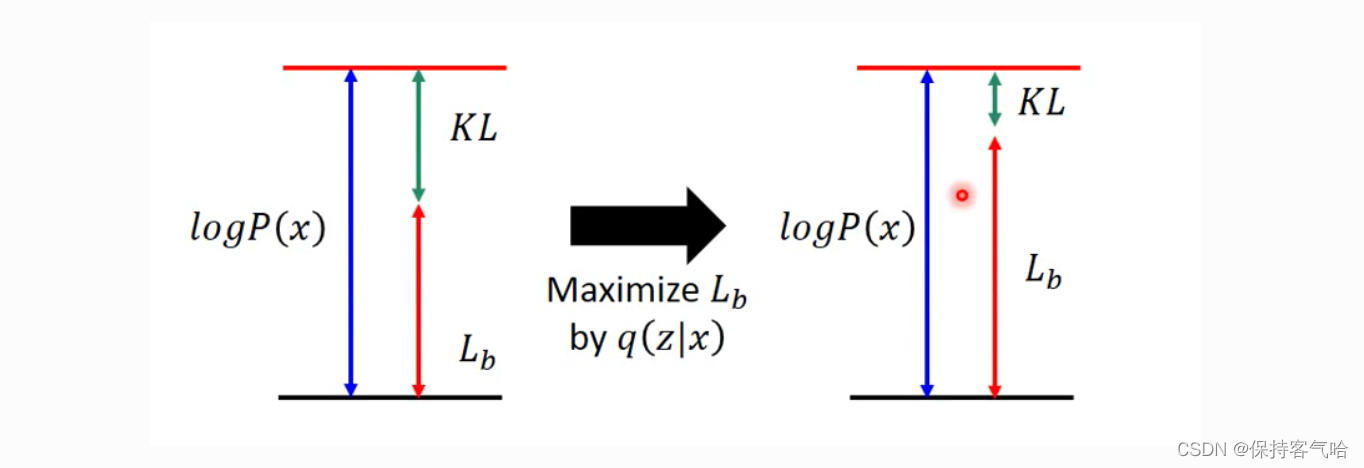
现在我们来求 Maxmize L b L_b Lb
L b = ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) d z = ∫ z q ( z ∣ x ) log P ( x ∣ z ) P ( z ) q ( z ∣ x ) d z = ∫ z q ( z ∣ x ) log P ( z ) q ( z ∣ x ) d z + ∫ z q ( z ∣ x ) log P ( x ∣ z ) d z = − D K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) + E q ( z ∣ x ) [ log P ( x ∣ z ) ] \begin{aligned} L_b &= \int_z q(z|x) \log \frac{P(z,x)}{q(z|x)} dz \\ &= \int_z q(z|x) \log \frac{P(x|z)P(z)}{q(z|x)} dz \\ &= \int_z q(z|x) \log\frac {P(z)}{q(z|x)} dz +\int_z q(z|x) \log P(x|z) dz \\ &= -D_{KL}(q(z|x) || P(z)) + E_{q(z|x)}[\log P(x|z)] \end{aligned} Lb=∫zq(z∣x)logq(z∣x)P(z,x)dz=∫zq(z∣x)logq(z∣x)P(x∣z)P(z)dz=∫zq(z∣x)logq(z∣x)P(z)dz+∫zq(z∣x)logP(x∣z)dz=−DKL(q(z∣x)∣∣P(z))+Eq(z∣x)[logP(x∣z)]
所以,求解 Maxmize L b L_b Lb,等价于求解KL(q(z|x)||P(z))的最小值和==$ E_{q(z|x)}[\log P(x|z)]$的最大值。==
-
我们先来求第一项,其实 − D K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) -D_{KL}(q(z|x) || P(z)) −DKL(q(z∣x)∣∣P(z))的展开式刚好等于: ∑ i = 1 J ( e x p ( σ i ) − ( 1 − σ i ) + ( m i ) 2 ) \sum _{i=1}^J (exp(\sigma_i)-(1-\sigma_i)+(m_i)^2) ∑i=1J(exp(σi)−(1−σi)+(mi)2),于是,第一项式子就是第二节VAE模型架构中第二个损失函数的由来,其实就是去调节NN’使得到的q(z|x)与标准正态分布约接近越好
-
接下来求第二项,注意到Maxmize$ E_{q(z|x)}[\log P(x|z)]$,也就是表明在给定求q(z|x)(编码器输出)的情况下p(x|z)(解码器输出)的值尽可能高,这其实就是一个类似于Auto-Encoder的损失函数(方差忽略不计的话),过程如下图所示:
-

-
我们要想从q(z|x)中sample一个data,就将x输入到NN中,产生 μ ′ ( x ) , σ ′ ( x ) \mu^\prime(x), \sigma^\prime(x) μ′(x),σ′(x),然后产生z,接下来我们要maxmize z产生x的几率,即要想输出maxmize log P(x|z)就需要让NN的输出 μ ( x ) \mu(x) μ(x) 与 x越接近越好
-
相关文章:

VAE-根据李宏毅视频总结的最通俗理解
1.VAE的直观理解 先简单了解一下自编码器,也就是常说的Auto-Encoder。Auto-Encoder包括一个编码器(Encoder)和一个解码器(Decoder)。其结构如下: 自编码器是一种先把输入数据压缩为某种编码, 后仅通过该编…...
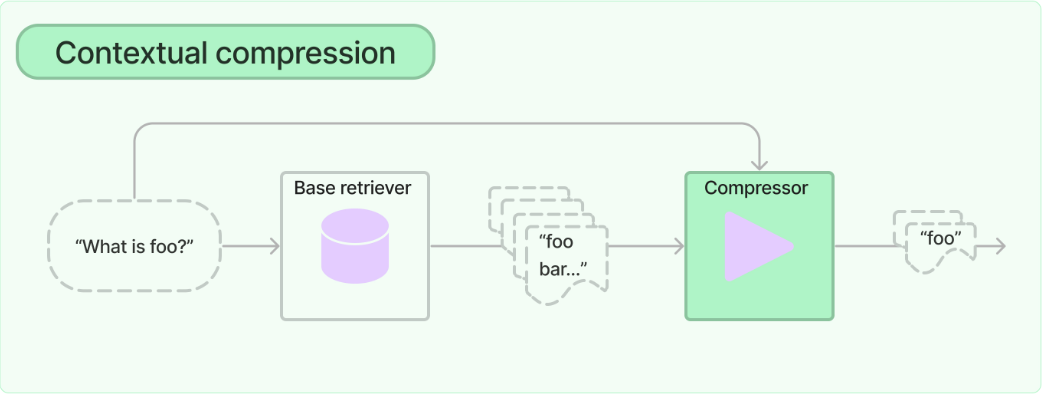
【LangChain】检索器之上下文压缩
LangChain学习文档 【LangChain】检索器(Retrievers)【LangChain】检索器之MultiQueryRetriever【LangChain】检索器之上下文压缩 上下文压缩 LangChain学习文档 概要内容使用普通向量存储检索器使用 LLMChainExtractor 添加上下文压缩(Adding contextual compression with an…...
uniapp 语音文本播报功能
最近uniapp项目上遇到一个需求 就是在接口调用成功的时候加上语音播报 , ‘创建成功’ ‘开始成功’ ‘结束成功’ 之类的。 因为是固定的文本 ,所以我先利用工具生成了 文本语音mp3文件,放入项目中,直接用就好了。 这里用到的工…...

腾讯云高IO型云服务器CPU型号处理器主频性能
腾讯云服务器高IO型CVM实例CPU处理器主频性能说明,高IO型云服务器具有高随机IOPS、高吞吐量、低访问延时等特点,适合对硬盘读写和时延要求高的高性能数据库等I/O密集型应用,腾讯云服务器网分享高IO型云服务器IT5和IT3的CPU处理器说明…...
【数据结构】实验八:树
实验八 树 一、实验目的与要求 1)理解树的定义; 2)掌握树的存储方式及基于存储结构的基本操作实现; 二、 实验内容 题目一:采用树的双亲表示法根据输入实现以下树的存储,并实现输入给定结点的双亲结点…...
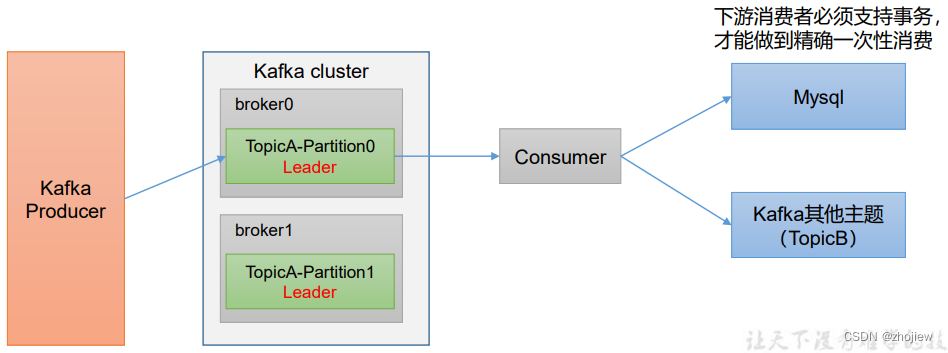
kafka消费者api和分区分配和offset消费
kafka消费者 消费者的消费方式为主动从broker拉取消息,由于消费者的消费速度不同,由broker决定消息发送速度难以适应所有消费者的能力 拉取数据的问题在于,消费者可能会获得空数据 消费者组工作流程 Consumer Group(CG&#x…...
【驱动开发day4作业】
头文件代码 #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t; #define PHY_LED1_ADDR 0X50006000 #define PHY_LED2_ADDR 0X50007000 #…...

Ubuntu 20.04 Ubuntu18.04安装录屏软件Kazam
1.在Ubuntu Software里面输入Kazam,就可以找不到这个软件,直接点击install就可以了 2.使用方法: 选择Screencast(录屏) Fullscreen(全屏)-----Windows(窗口)--------Ar…...

ADC 的初识
ADC介绍 Q: ADC是什么? A: 全称:Analog-to-Digital Converter,指模拟/数字转换器 ADC的性能指标 量程:能测量的电压范围分辨率:ADC能辨别的最小模拟量,通常以输出二进制数的位数表示,比如&am…...

MMdetection框架速成系列 第07部分:数据增强的N种方法
MMdetection框架实现数据增强的N种方法 1 为什么要进行数据增强2 数据增强的常见误区3 常见的六种数据增强方式3.1 随机翻转(RandomFlip)3.2 随机裁剪(RandomCrop)3.3 随机比例裁剪并缩放(RandomResizedCrop࿰…...

基于Kitti数据集的智能驾驶目标检测系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于Kitti数据集的智能驾驶目标检测系统可用于日常生活中检测与定位行人(Pedestrian)、面包车(Van)、坐着的人(Person Sitting)、汽车(Car)、卡车(Truck…...

4.4. 深拷贝 vs 浅拷贝
文章目录 浅拷贝:对基本数据类型进行值传递,对引用数据类型进行引用传递般的拷贝,此为浅拷贝。深拷贝:对基本数据类型进行值传递,对引用数据类型,创建一个新的对象,并复制其内容,此为…...
网络安全(黑客)自学建议笔记
前言 网络安全,顾名思义,无安全,不网络。现如今,安全行业飞速发展,我们呼吁专业化的 就职人员与大学生 ,而你,认为自己有资格当黑客吗? 本文面向所有信息安全领域的初学者和从业人员…...
Linux CentOS快速安装VNC并开启服务
以下是在 CentOS 上安装并开启 VNC 服务的步骤: 安装 VNC 服务器软件包。运行以下命令: sudo yum install tigervnc-server 输出 $ sudo yum install tigervnc-server Loaded plugins: fastestmirror, langpacks Repository epel is missing name i…...
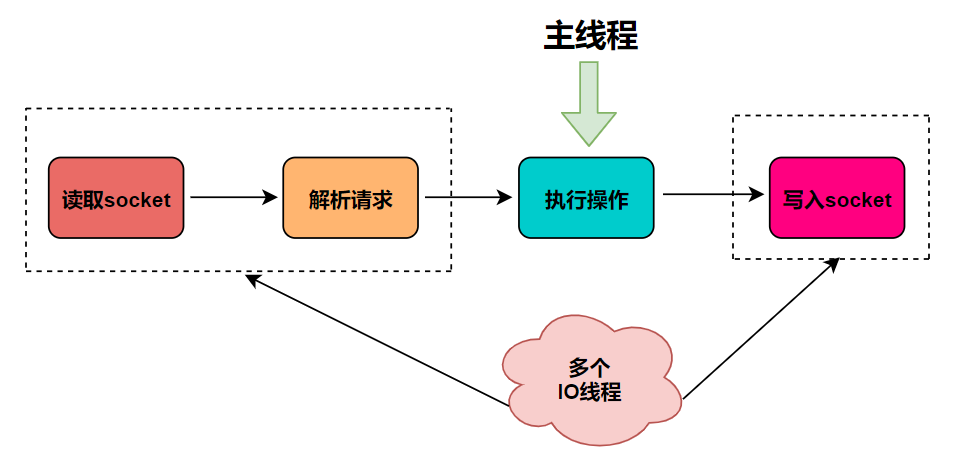
redis到底几个线程?
通常我们说redis是单线程指的是从接收客户端请求->解析请求->读写->响应客户端这整个过程是由一个线程来完成的。这并不意味着redis在任何场景、任何版本下都只有一个线程 为何用单线程处理数据读写? 内存数据储存已经很快了 redis相比于mysql等数据库是…...

mysql修改UUID
mysql修改UUID 问题描述:集群搭建时克隆主服务的镜像导致所有节点的服务UUID都一致,此时在集群中添加节点时会提示UUID冲突报错。 解决方案 1、利用uuid函数生成新的uuid mysql> select uuid(); -------------------------------------- | uuid() …...
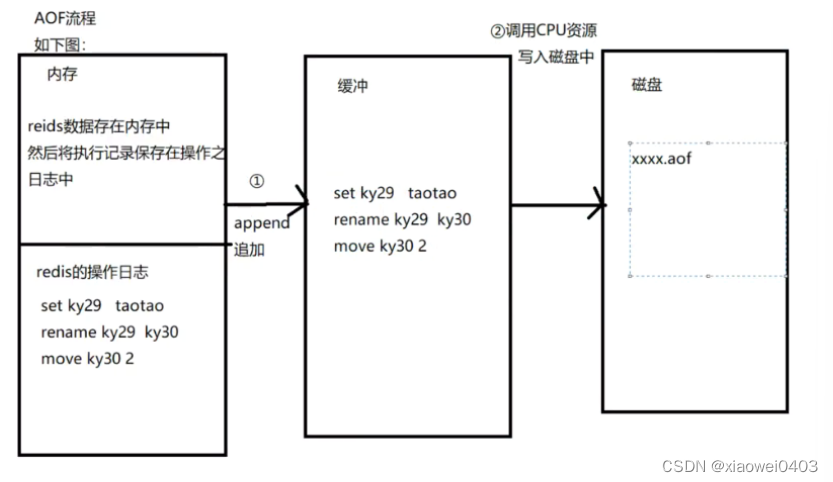
NoSQL之redis配置与优化
NoSQL之redis配置与优化 高可用持久化功能Redis提供两种方式进行持久化1.触发条件手动触发自动触发 执行流程优缺点缺点:优势AOF出发规则: AOF流程AOF缺陷和优点 NoSQL之redis配置与优化 mysql优化 1线程池优化 2硬件优化 3索引优化 4慢查询优化 5内…...

Python单例模式介绍、使用
一、单例模式介绍 概念:单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供访问该实例的全局访问点。 功能:单例模式的主要功能是确保在应用程序中只有一个实例存在。 优势: 节省系统资源:由…...
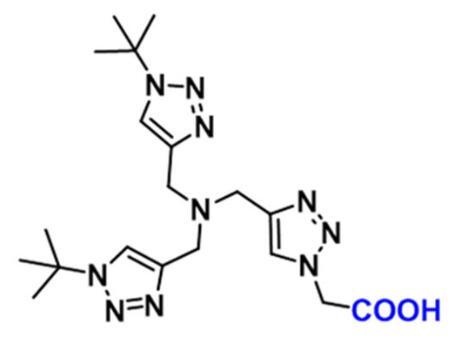
1334179-85-9,BTTAA,是各种化学生物学实验中生物偶联所需
资料编辑|陕西新研博美生物科技有限公司小编MISSwu BTTAA试剂 | 基础知识概述(部分): 中文名称:2-[4-({双[(1-叔丁基-1H-1,2,3-三唑-4-基)甲基]氨基}甲基)-1H-1,2,3-三唑-1-基]乙酸 英文名称:BTTAA CAS号:1334179-8…...

Linux系统中的SQL语句
本节主要学习,SQL语句的语句类型,数据库操作,数据表操作,和数据操作等。 文章目录 一、SQL语句类型 DDL DML DCL DQL 二、数据库操作 1.查看 2.创建 默认字符集 指定字符集 3.进入 4.删除 5.更改 库名称 字符集 6…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

