Boyer-Moore 投票算法
这里先贴题目:
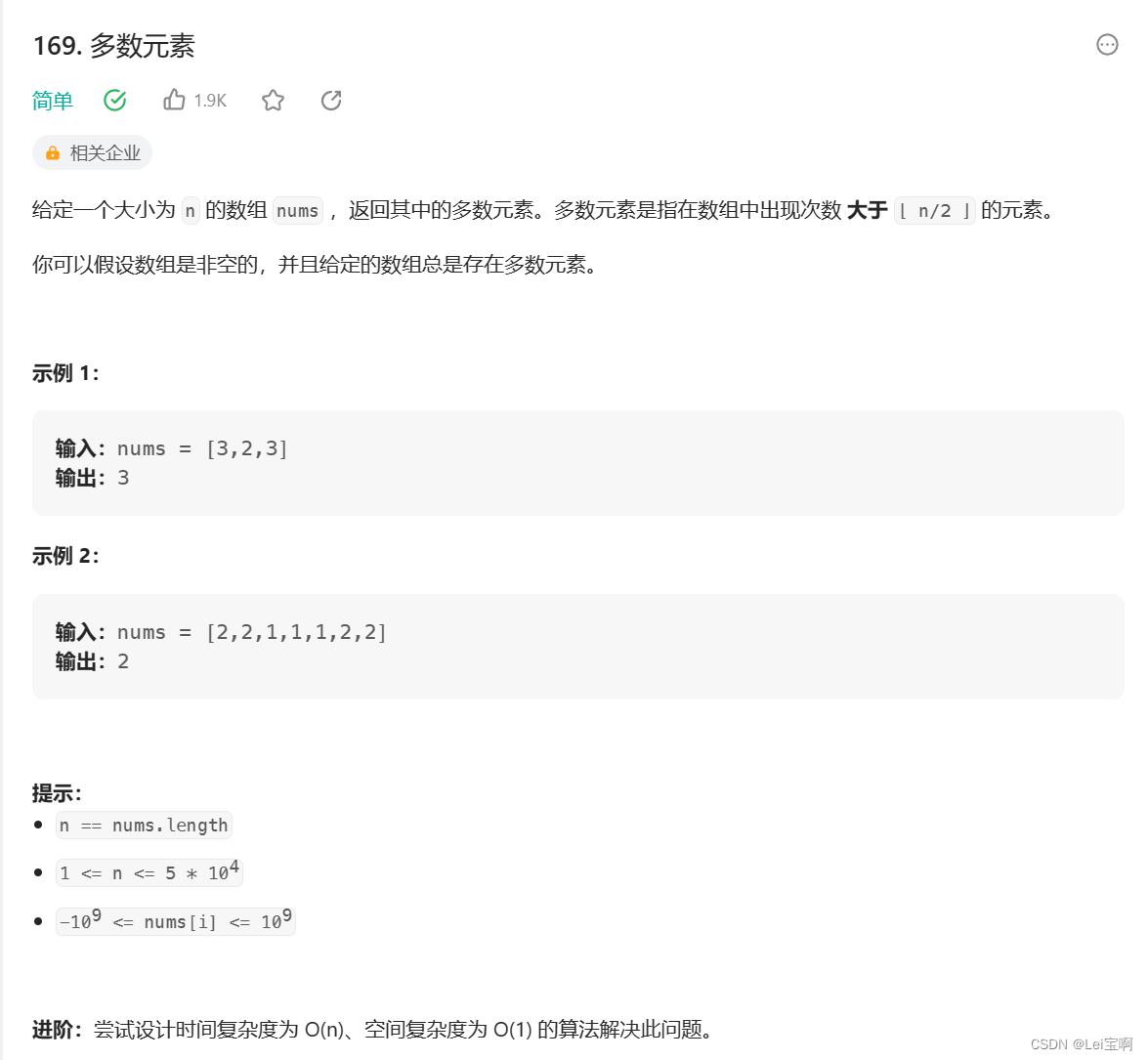
Boyer-Moore 投票算法:
通俗点来讲,就是占领据点,像攻城那样,对消。
当你的据点有人时对消,无人时就占领。
这道题使用该算法可实现时间复杂度为O(n),空间复杂度为O(1),接下来看代码:
int majorityElement(int* nums, int numsSize) {int amzing = nums[0];int count = 0;for (int i = 0; i < numsSize; i++){if (amzing == nums[i])count++;else if (count == 0){amzing = nums[i];count++;}elsecount--;}return amzing;
}我们定义一个amzing先记录数组第一个数字,并且数量为0,然后遍历整个数组,当count不为0时,数字不同时相消,数字相同时增加,当count为0时,amzing换其他数字,再增加数量。
通俗点讲:定义一个士兵,数量为0,遍历所有人,当count不为0,如果数字不同,就是遇到敌人,同归于尽,数字相同,遇到友军就加入。当count等于0,据点无人,哪个数字也可以占领。但是有一个阵营的人数占了大半,无论怎么对拼相消,剩下的一定是那个阵营的,也就是那个大半的数字。
排序:
int cmp(void* p1,void* p2)
{return *(int*)p1 - *(int*)p2;
}int majorityElement(int* nums, int numsSize){qsort(nums,numsSize,4,cmp);return nums[numsSize/2];
}相关文章:

Boyer-Moore 投票算法
这里先贴题目: Boyer-Moore 投票算法: 通俗点来讲,就是占领据点,像攻城那样,对消。 当你的据点有人时对消,无人时就占领。 这道题使用该算法可实现时间复杂度为O(n),空间复杂度为O(1),接下来看…...

C# 翻转二叉树
226 翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1] 示例 2: 输入:root [2,1,3] 输出:…...
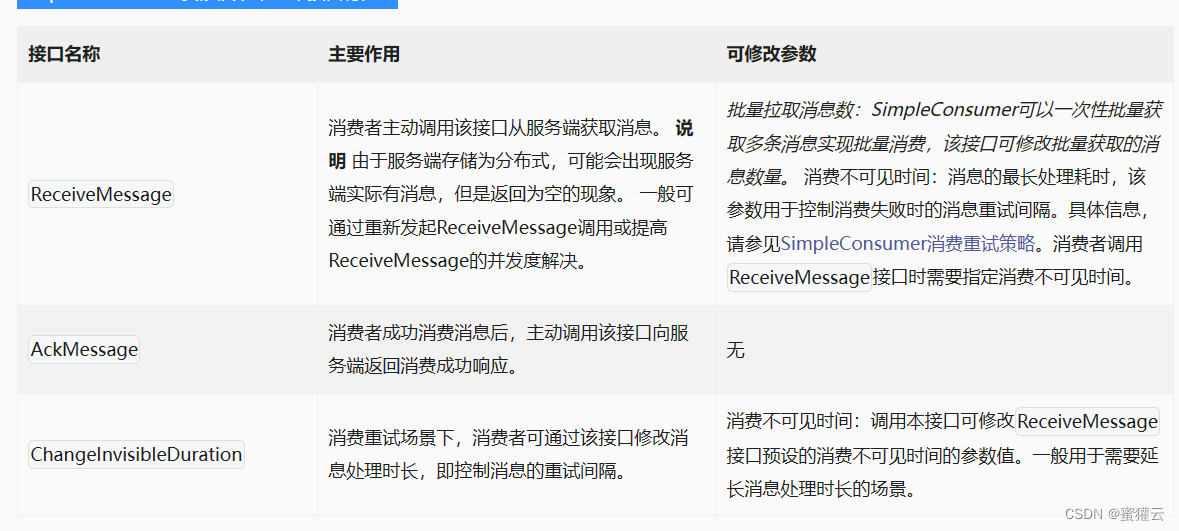
RocketMQ教程-(5)-功能特性-消费者分类
Apache RocketMQ 支持 PushConsumer 、 SimpleConsumer 以及 PullConsumer 这三种类型的消费者,本文分别从使用方式、实现原理、可靠性重试和适用场景等方面为您介绍这三种类型的消费者。 背景信息 Apache RocketMQ 面向不同的业务场景提供了不同消费者类型&…...
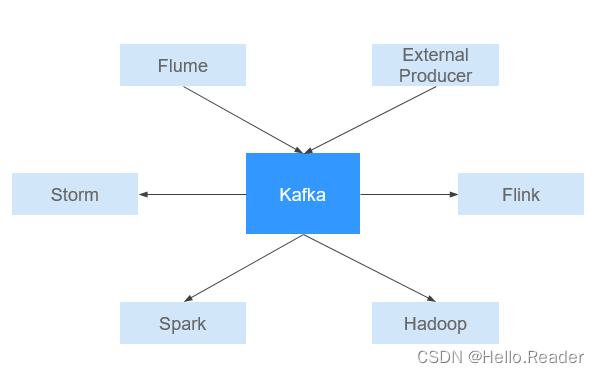
Kafka原理剖析
一、简介 Kafka是一个分布式的、分区的、多副本的消息发布-订阅系统,它提供了类似于JMS的特性,但在设计上完全不同,它具有消息持久化、高吞吐、分布式、多客户端支持、实时等特性,适用于离线和在线的消息消费,如常规的…...
word怎么转换成pdf?分享几种转换方法
word怎么转换成pdf?将Word文档转换成PDF文件有几个好处。首先,PDF文件通常比Word文档更容易在不同设备和操作系统上查看和共享。其次,PDF文件通常比Word文档更难以修改,这使得它们在需要保护文件内容的情况下更加安全可靠。最后&a…...

基于XDMA 中断模式的 PCIE3.0 QT上位机与FPGA数据交互架构 提供工程源码和QT上位机源码
目录 1、前言2、我已有的PCIE方案3、PCIE理论4、总体设计思路和方案图像产生、发送、缓存数据处理XDMA简介XDMA中断模式图像读取、输出、显示QT上位机及其源码 5、vivado工程详解6、上板调试验证7、福利:工程代码的获取 1、前言 PCIE(PCI Express&#…...
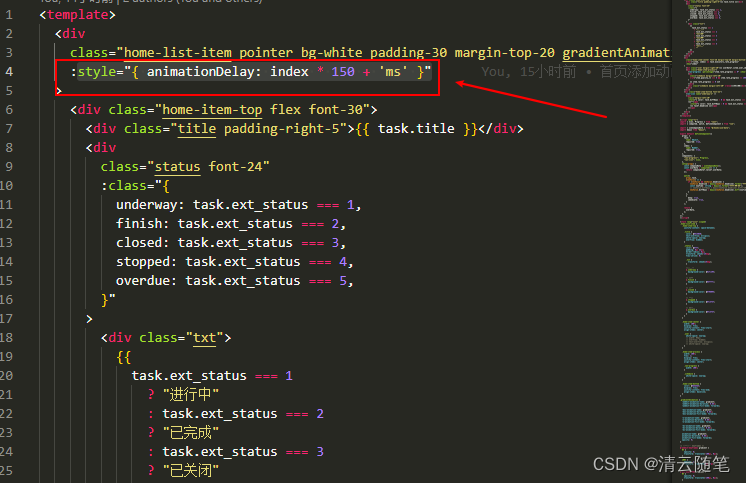
Vue 中通用的 css 列表入场动画效果
css 代码 .gradientAnimation {animation-name: gradient;animation-duration: 0.85s;animation-fill-mode: forwards;opacity: 0; }/* 不带前缀的放到最后 */ keyframes gradient {0% {opacity: 0;transform: translate(-100px, 0px);}100% {opacity: 1;transform: translate…...

微分流形2:流形上的矢量场和张量场
来了来了,切向量,切空间。流形上的所有的线性泛函的集合,注意是函数的集合。然后取流形上的某点p,它的切向量为,线性泛函到实数的映射。没错,是函数到实数的映射,是不是想到了求导。我们要逐渐熟…...
C++数组、向量和列表的练习
运行代码: //C数组、向量和列表的练习 #include"std_lib_facilities.h"int main() try {int ii[10] { 0,1,2,3,4,5,6,7,8,9 };for (int i 0; i < 10; i)//把数组中的每个元素值加2ii[i] 2;vector<int>vv(10);for (int i 0; i < 10; i)vv…...
视频剪辑矩阵分发系统Unable to load FFProbe报错技术处理?
问题一 报错处理 对于视频剪辑矩阵分发系统中出现的“Unable to load FFProbe”报错问题,可以采取以下技术处理措施进行解决。 1.检查系统中是否正确安装了FFProbe工具,并确保其路径正确配置。 2.检查系统环境变量是否正确设置,包括FFPr…...
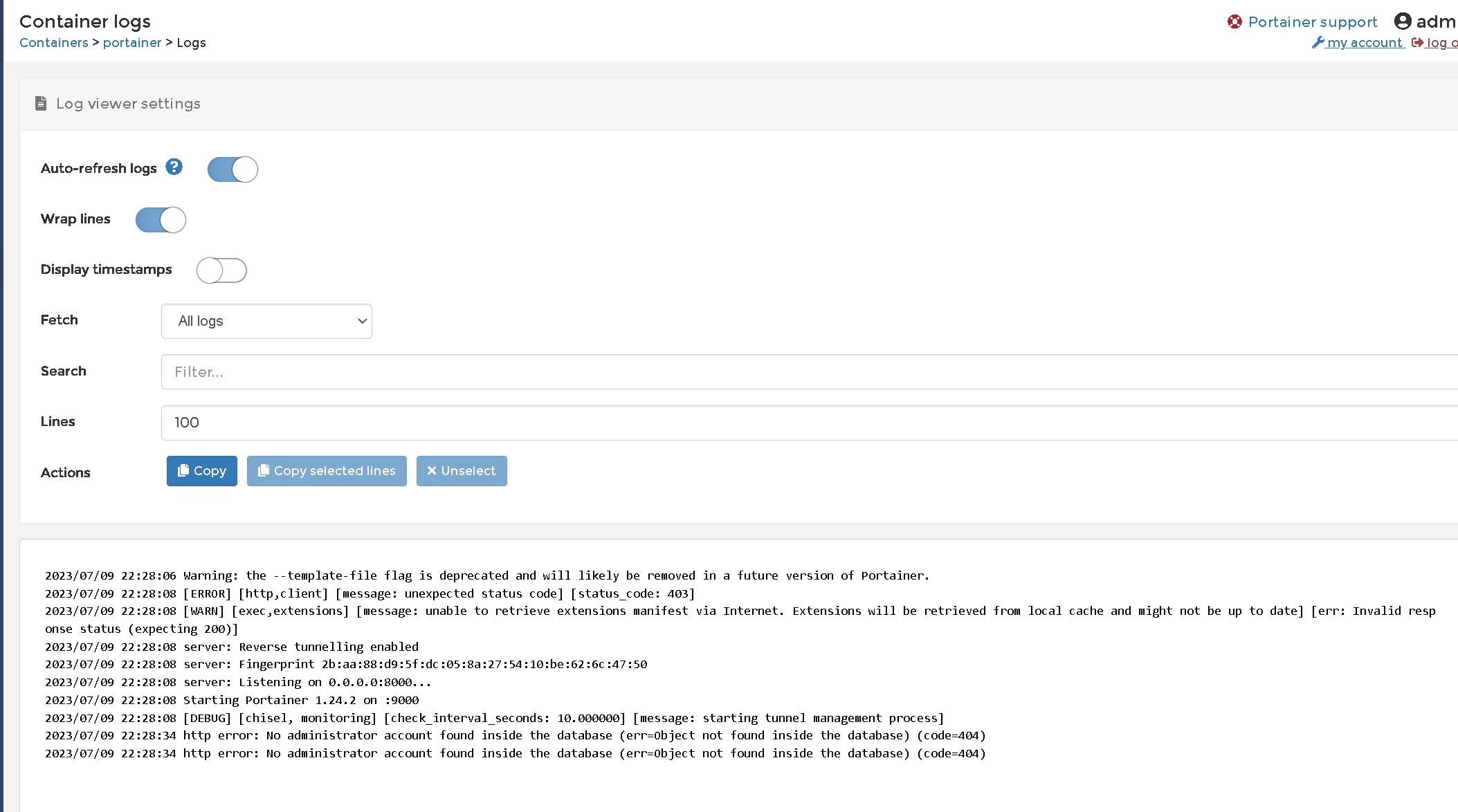
Docker轻量级可视化工具Portainer
Portainer是一个轻量级的管理UI界面,用于管理Docker容器、镜像、卷和网络。它支持端口映射、容器启动、停止、删除、日志查看等功能,同时也提供了可视化的监控和统计功能,可以快速轻松的管理多个Docker主机。Portainer不需要额外安装依赖&…...

功率放大器在电光调制中的应用有哪些
电光调制是一种利用光电效应将电信号转化为光信号的技术。在实现电光调制的过程中,功率放大器作为一个重要的组件,具有对输入电信号进行放大和控制的功能。本文将介绍功率放大器的基本原理、特点以及在电光调制中的应用。 基本原理 功率放大器是一种能够…...

MyBatis入门程序
1.MyBatis 入门程序开发步骤 SqlSession:代表Java程序和数据库之间的会话。(HttpSession是Java程序和浏览器之间的会话) SqlSessionFactory:是“生产”SqlSession的“工厂”。 工厂模式:如果创建某一个对象ÿ…...

C++快速切换 头文件和源文件
有没有一种快速的方法 , 将头文件中的声明 直接在源文件中自动写出来, 毕竟头文件中已经有声明了, 我只需要写具体实现就行了,没有必要把声明的部分再敲一遍在 Visual Studio 中,你可以使用快速生成函数定义的功能来实…...
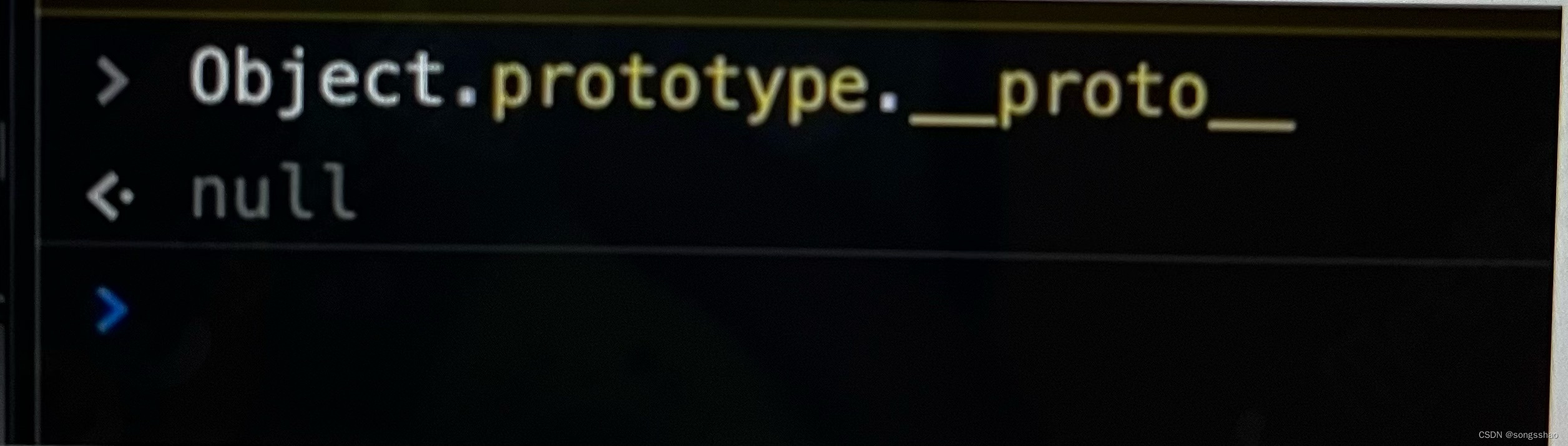
对原型、原型链的理解
在 JavaScript 中是使用构造两数来新建一个对象的,每一个构造函数的内部都有一个 prototype 属性,它的属性值是一个对象,这个对象包含了可以由该构造西数的所有实例共享的属性和方法。当使用构造函数新建一个对象后,在这个对象的内…...

7月26日,每日信息差
1、日本经产省将讨论让消费者负担核电站重启费。若被采用,那么即便是与把源自可再生能源作为卖点的新电力公司签约的消费者,也将负担重启核电站的费用 2、国家发改委:电厂存煤和出力均达历史同期最高水平 3、国家深改委:全国统调…...

git修改已经push后的commit注释
回到倒数第8次提交 git rebase -i HEAD~8修改注释,然后把最前面的pick改成edit 修改注释 git commit --amendrebase确认 git rebase --continue强制提交 git push -f origin master参考:https://blog.csdn.net/qq_16942727/article/details/1260355…...

网络云存储服务器,数据库服务器|PetaExpress
云存储服务器是什么? 云存储服务器是一种在线存储(英语:Cloud storage)该模式是将数据存储在通常由第三方托管的多个虚拟服务器上,而不是独家服务器上。 云存储服务器有几种结构 架构方法分为两类:一类是通过服务进行架构&…...

java语法基础--基本数据类型
一、数据类型概括 1、整数类型 2、浮点型 3、布尔类型 4、字符类型 二、数据类型的使用 1、整数类型的使用 超出类型范围 //1.1 定义一个byte类型的变量,并且设置它超过byte类型范围// 如果定义的数值在byte类型范围内,那么就能正常使用,//…...
uniapp 微信小程序 预览pdf方法
效果图: 1、在小程序中 // #ifdef MP */ 是区分运行的环境,在小程序中可使用如下方法uni.downloadFile({url: item.link,//文件地址success: function (res) {var filePath res.tempFilePath;uni.openDocument({filePath: filePath,showMenu: false…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
