48. 旋转图像
题目介绍
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
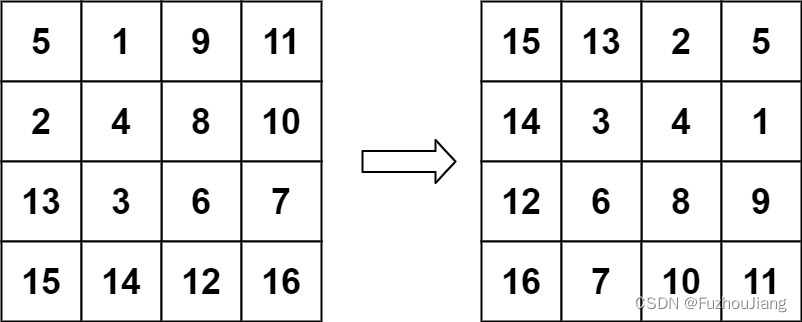
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
解答
class Solution {
public:void rotate(vector<vector<int>>& matrix) {// 先上下交换元素,后对角交换int size = matrix.size();int i = 0, j = size - 1;while(i < j){vector<int> temp = matrix[i];matrix[i] = matrix[j];matrix[j] = temp;i++; j--;}// 对角交换for(int i = 0; i < size; ++i){for(int j = i + 1; j < size; ++j){int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}}
};
相关文章:

48. 旋转图像
题目介绍 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],[4,5,6]…...

“深入解析Spring Boot:从入门到精通的完整指南“
标题:深入解析Spring Boot:从入门到精通的完整指南 摘要:本文将深入解析Spring Boot框架,从入门到精通,为读者提供全面的指南。我们将介绍Spring Boot的基本概念、核心特性以及使用方法,并通过示例代码演示…...

【C++】C++11——包装器
文章目录 1. function包装器1.1 遇到的问题1.2 包装器的定义1.3 解决问题1.4 包装器的其他应用 2. bind2.1 bind的定义2.2 bind包装器绑定固定参数2.3 bind包装器调整传参顺序2.4 bind包装器的意义 1. function包装器 1.1 遇到的问题 我们首先来看一行代码: ret …...
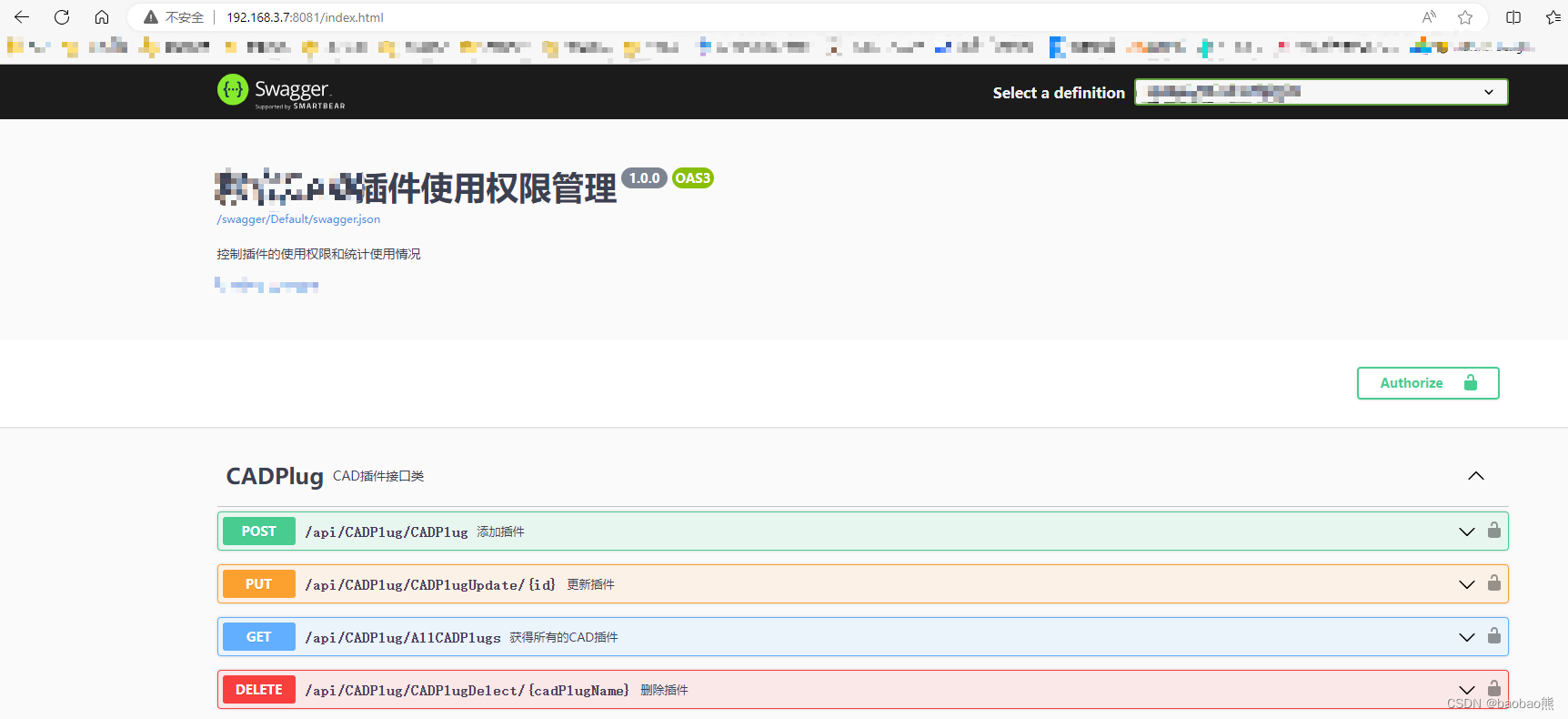
插件使用权限管理软件(三)WebAPI项目IIS部署
前言 前面完成了WebAPI项目的接口服务类编写工作,接下来讲把项目部署到服务器的IIS上,让系统运行起来。 一. 项目发布 右键项目RightsManagementSystems.Web.Entry 选择“发布”选项 弹出发布选项界面,选择“文件夹”,点击下一步…...

[算法很美打卡] 多维数组篇 (打卡第二天)
文章目录 Z形打印边界为1的最大子方阵 Z形打印 package 每日算法学习打卡.算法打卡.七月份.七月二十七号;public class test1 {public static void main(String[] args) {int[][] matrix {{1, 2, 3, 4},{5, 6, 7, 8},{9, 10, 11, 12},};print(matrix);}static void print(int[…...
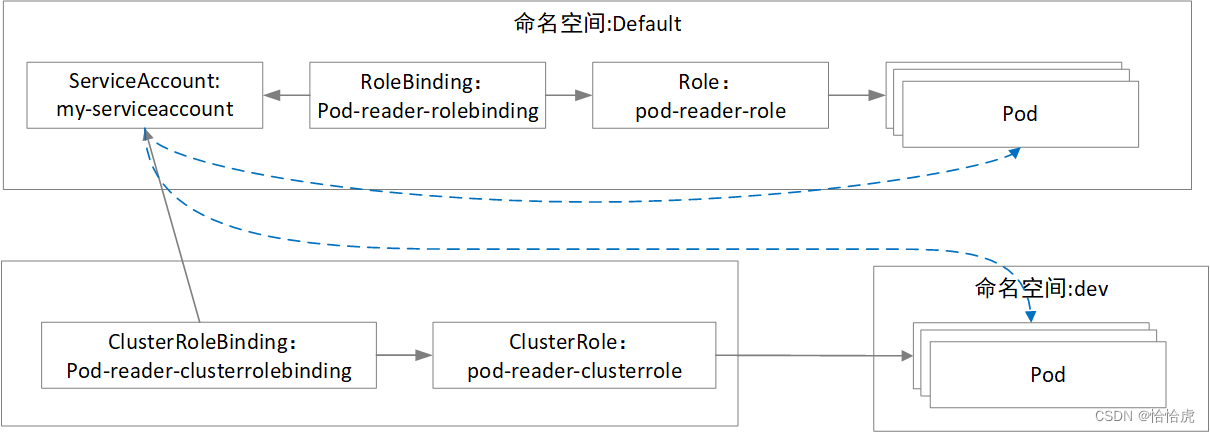
K8S初级入门系列之十一-安全
一、前言 安全是K8S重要的特性,在K8S初级入门系列之四-Namespace/ConfigMap/Secret章节,我们已经已经了解了Namespace,Secret与安全相关的知识。本篇将梳理K8S在安全方面的策略。主要包括两个方面,API安全访问策略以及Pod安全策略…...

【雕爷学编程】MicroPython动手做(02)——尝试搭建K210开发板的IDE环境6
#尝试搭建K210的Micropython开发环境(Win10) #实验程序之六:测试Microphone阵列算法 #尝试搭建K210的Micropython开发环境(Win10) #实验程序之六:测试Microphone阵列算法from Maix import MIC_ARRAY as mi…...

“深入解析Spring Boot:从入门到精通“
标题:深入解析Spring Boot:从入门到精通 摘要:本文深入解析了Spring Boot框架,从入门到精通,包括核心概念、特性、使用方法和示例代码。通过阅读本文,读者将对Spring Boot有一个全面的了解,并可…...
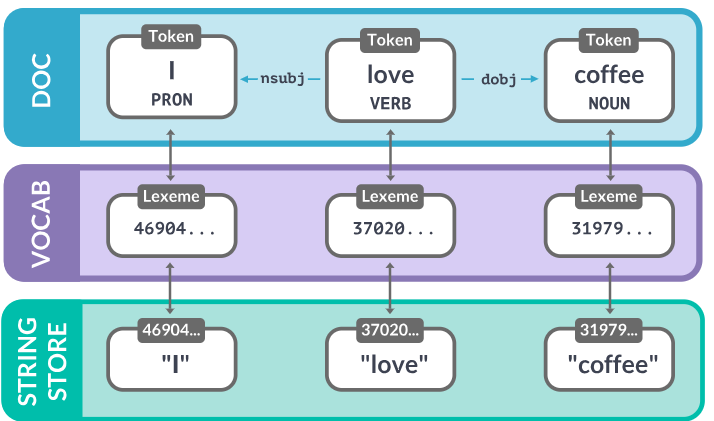
[自然语言处理] 自然语言处理库spaCy使用指北
spaCy是一个基于Python编写的开源自然语言处理库。基于自然处理领域的最新研究,spaCy提供了一系列高效且易用的工具,用于文本预处理、文本解析、命名实体识别、词性标注、句法分析和文本分类等任务。 spaCy的官方仓库地址为:spaCy-github。本…...
】第6課 拓哉もさしみを食べたがってします)
【新日语(2)】第6課 拓哉もさしみを食べたがってします
第6課 拓哉もさしみを食べたがっています 注释: 食べたがっています:食べ+たが+ています、想要吃。たがっています:たがる+ています、想要。 练习A 一、 例句 わたしは、明日、デパートへ行きます。 …...

uni-app 经验分享,从入门到离职(一)——初始 uni-app,快速上手(文末送书福利1.0)
文章目录 📋前言🎯什么是 uni-app🎯创建第一个 uni-app 项目🧩前期工作🧩创建项目(熟悉默认项目、结构)🧩运行项目 📝最后🎯文末送书🔥参与方式 &…...
Python爬虫实例之淘宝商品页面爬取(api接口)
可以使用Python中的requests和BeautifulSoup库来进行网页爬取和数据提取。以下是一个简单的示例: import requests from bs4 import BeautifulSoupdef get_product_data(url):# 发送GET请求,获取网页内容headers {User-Agent: Mozilla/5.0 (Windows NT…...

并发编程 | CompletionService - 如何优雅地处理批量异步任务
引言 上一篇文章中,我们详细地介绍了 CompletableFuture,它是一种强大的并发工具,能帮助我们以声明式的方式处理异步任务。虽然 CompletableFuture 很强大,但它并不总是最适合所有场景的解决方案。 在这篇文章中,我们…...
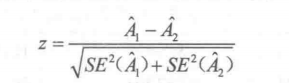
医学案例|ROC曲线之面积对比
一、案例介绍 为评价CT和CT增强对肝癌的诊断效果,共检查了32例患者,每例患者分别用两种方法检查,由医生盲态按4个等级诊断,最后经手术病理检查确诊其中有16例患有肝癌,评价CT个CT增强对肝癌是有有诊断效果并且试着比较…...

Kotlin线程的基本用法
线程的基本用法 新建一个类继承自Thread,然后重写父类的run()方法 class MyThread : Thread() {override fun run() {// 编写具体的逻辑} }// 使用 MyThread().start()实现Runnable接口 class MyThread : Runnable {override fun run() {// 编写具体的逻辑} }// …...

2.03 PageHelper分页工具
步骤1:在application.yml中添加分页配置 # 分页插件配置 pagehelper:helperDialect: mysqlsupportMethodsArguments: true步骤2:在顶级工程pom文件下引入分页插件依赖 <!--5.PageHelper --> <dependency><groupId>com.github.pagehe…...

VUE中使用ElementUI组件的单选按钮el-radio-button实现第二点击时取消选择的功能
页面样式为: html 代码为: 日志等级: <el-radio-group v-model"logLevel"><el-radio-button label"DEBUG" click.native.prevent"changeLogLevel(DEBUG)">DEBUG</el-radio-button><el-r…...

瓴羊Quick BI:可视化大屏界面设计满足企业个性需求
大数据技术成为现阶段企业缩短与竞争对手之间差距的重要抓手,依托以瓴羊Quick BI为代表的工具开展内部数据处理分析工作,也成为诸多企业持续获取竞争优势的必由之路。早年间国内企业倾向于使用进口BI工具,但随着瓴羊Quick BI等一众国内数据处…...

617. 合并二叉树
题目 题解一:递归 /*** 递归* param root1* param root2* return*/public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {//结束条件if (root1 null) {return root2;} //结束条件if (root2 null) {return root1;}//两节点数值相加TreeNode me…...
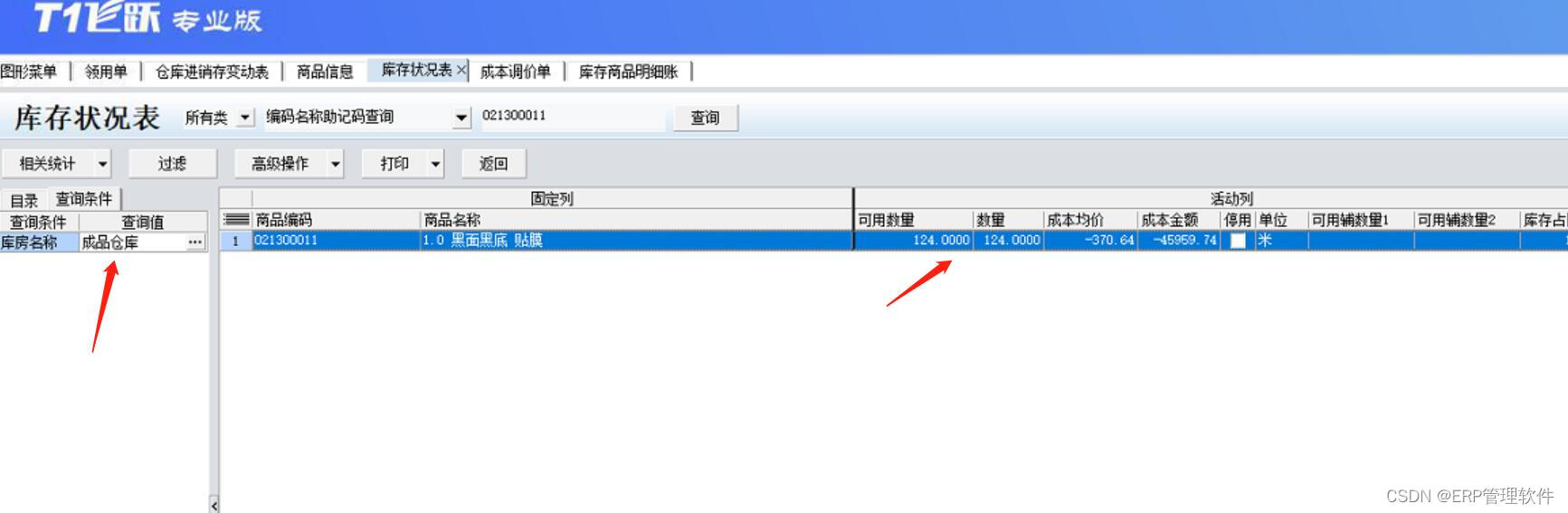
【T1】存货成本异常、数量为零金额不为零的处理方法。
【问题描述】 使用T1飞跃专业版的过程中, 由于业务问题或者是操作问题, 经常会遇到某个商品成本异常不准确, 或者是遇到数量为0金额不为0的情况,需要将其成本调为0。 但是T1软件没有出入库调整单,并且结账无法针对数量…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
