【新日语(2)】第6課 拓哉もさしみを食べたがってします
第6課 拓哉もさしみを食べたがっています
注释:
- 食べたがっています:食べ+たが+ています、想要吃。
- たがっています:たがる+ています、想要。
练习A
一、
例句
わたしは、明日、デパートへ行きます。
我明天要去百货商店。
わたしは、明日、デパートへ行こうと思います。
我明天想去百货商店。
注释:
- 行こうと思います:行こう+と+思います、想去。
- 行こう:【意志形】。
1)
明日は、早く起きます。
明天,我会早起。
明日は、早く起きようと思います。
我想明天起得早一些。
2)
今晩、カレーを食べます。
今晚,我要吃咖喱。
今晩、カレーを食べようと思います。
今晚、我想吃咖喱。
3)
お正月には日本へ帰ります。
新年的时候我会回日本。
注释:
- お正月:新年。
お正月には日本へ帰ろうと思います。
我想在新年的时候回日本。
4)
今日は、熱があるので、休みます。
因为今天有点发热,所以我要休息。
今日は、熱があるので、休もうと思います。
因为今天有点发热,所以我打算去休息。
注释:
- 「ので、」: 【连接词】“因为”,“所以”。用于连接原因和结果。
二、例句
例句
明日は、たぶん、雪が降ります。
明天可能会下雪。
明日は、雪が降るだろうと思います。
我觉得明天会下雪吧。
注释:
- 降るだろうと:降る+だろう+と,“下”。
- だろう:【意志形】,“吧”,表猜测。
1)
来年は、たぶん、景気が良くなります。
可能,明年经济会好转。
注释:
- 「良くなります」:会好转,会变好。
- 「なります」:【后缀】表示事物变化。
三、例句
わたしは来年、ヨーロッパへ行きます。
我明年将去欧洲。
わたしは来年、ヨーロッパへ行くつもりだ。
我打算明年去欧洲。
注释:
- 行くつもりだ:行く+つもりだ,打算去。
- ~つもりだ:【句型】打算。
- つもり:n. 打算。加动词最简单的形——辞书形,所以这里用「行く」。
四、例句
子どもは何でも知りたいと思っています。
孩子们想知道所有的事情。
注释:
- 知りたい:想知道。
- -たい:【助词】想。
子どもは何でも知りたがります。
孩子们总是想知道所有的事情。
五、例句
子どもはおもちゃが欲しいです。
孩子想要玩具。
注释:
- おもちゃ:玩具。
子どもがおもちゃを欲しがっています。
孩子(现在)想要玩具。
六、例句
時々、家族でカラオケをします。
有时,我们全家会去唱卡拉OK。
家族でカラオケすることがあります。
我们全家有时会去唱卡拉OK。
注释:
- することがあります:する+ことがあります、する是原形,“有时会去”。したことがあります,“做过某事”。
相关文章:
】第6課 拓哉もさしみを食べたがってします)
【新日语(2)】第6課 拓哉もさしみを食べたがってします
第6課 拓哉もさしみを食べたがっています 注释: 食べたがっています:食べ+たが+ています、想要吃。たがっています:たがる+ています、想要。 练习A 一、 例句 わたしは、明日、デパートへ行きます。 …...

uni-app 经验分享,从入门到离职(一)——初始 uni-app,快速上手(文末送书福利1.0)
文章目录 📋前言🎯什么是 uni-app🎯创建第一个 uni-app 项目🧩前期工作🧩创建项目(熟悉默认项目、结构)🧩运行项目 📝最后🎯文末送书🔥参与方式 &…...
Python爬虫实例之淘宝商品页面爬取(api接口)
可以使用Python中的requests和BeautifulSoup库来进行网页爬取和数据提取。以下是一个简单的示例: import requests from bs4 import BeautifulSoupdef get_product_data(url):# 发送GET请求,获取网页内容headers {User-Agent: Mozilla/5.0 (Windows NT…...

并发编程 | CompletionService - 如何优雅地处理批量异步任务
引言 上一篇文章中,我们详细地介绍了 CompletableFuture,它是一种强大的并发工具,能帮助我们以声明式的方式处理异步任务。虽然 CompletableFuture 很强大,但它并不总是最适合所有场景的解决方案。 在这篇文章中,我们…...
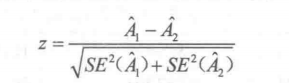
医学案例|ROC曲线之面积对比
一、案例介绍 为评价CT和CT增强对肝癌的诊断效果,共检查了32例患者,每例患者分别用两种方法检查,由医生盲态按4个等级诊断,最后经手术病理检查确诊其中有16例患有肝癌,评价CT个CT增强对肝癌是有有诊断效果并且试着比较…...

Kotlin线程的基本用法
线程的基本用法 新建一个类继承自Thread,然后重写父类的run()方法 class MyThread : Thread() {override fun run() {// 编写具体的逻辑} }// 使用 MyThread().start()实现Runnable接口 class MyThread : Runnable {override fun run() {// 编写具体的逻辑} }// …...

2.03 PageHelper分页工具
步骤1:在application.yml中添加分页配置 # 分页插件配置 pagehelper:helperDialect: mysqlsupportMethodsArguments: true步骤2:在顶级工程pom文件下引入分页插件依赖 <!--5.PageHelper --> <dependency><groupId>com.github.pagehe…...

VUE中使用ElementUI组件的单选按钮el-radio-button实现第二点击时取消选择的功能
页面样式为: html 代码为: 日志等级: <el-radio-group v-model"logLevel"><el-radio-button label"DEBUG" click.native.prevent"changeLogLevel(DEBUG)">DEBUG</el-radio-button><el-r…...

瓴羊Quick BI:可视化大屏界面设计满足企业个性需求
大数据技术成为现阶段企业缩短与竞争对手之间差距的重要抓手,依托以瓴羊Quick BI为代表的工具开展内部数据处理分析工作,也成为诸多企业持续获取竞争优势的必由之路。早年间国内企业倾向于使用进口BI工具,但随着瓴羊Quick BI等一众国内数据处…...

617. 合并二叉树
题目 题解一:递归 /*** 递归* param root1* param root2* return*/public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {//结束条件if (root1 null) {return root2;} //结束条件if (root2 null) {return root1;}//两节点数值相加TreeNode me…...
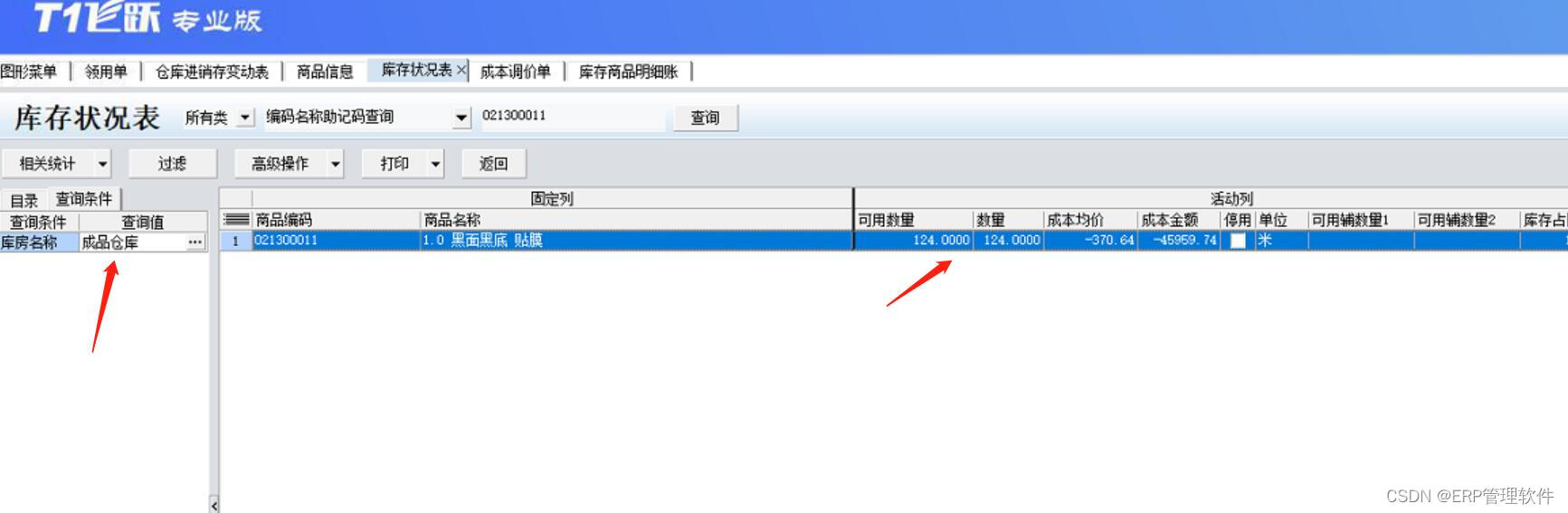
【T1】存货成本异常、数量为零金额不为零的处理方法。
【问题描述】 使用T1飞跃专业版的过程中, 由于业务问题或者是操作问题, 经常会遇到某个商品成本异常不准确, 或者是遇到数量为0金额不为0的情况,需要将其成本调为0。 但是T1软件没有出入库调整单,并且结账无法针对数量…...
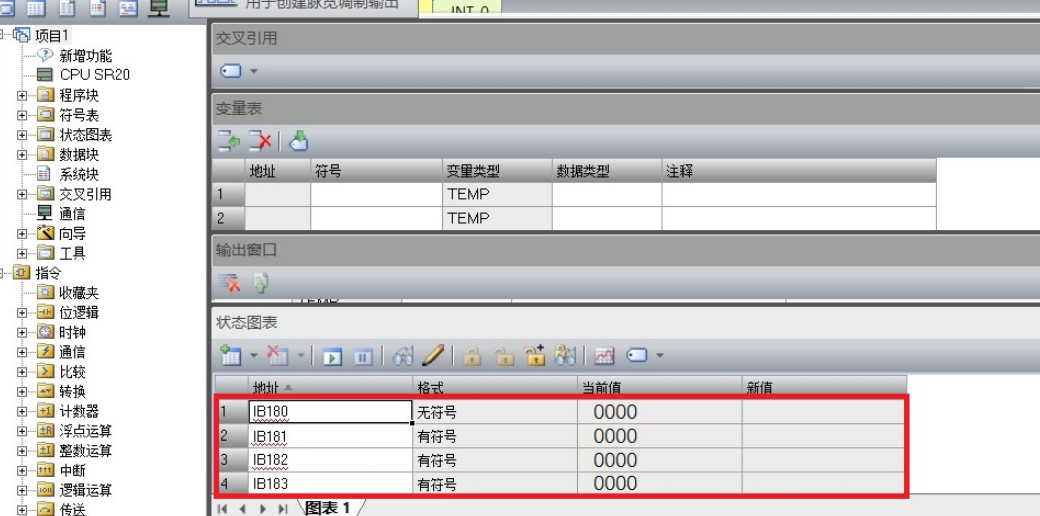
EtherNet IP转PROFINET网关连接西门子与欧姆龙方法
本文主要介绍了捷米特JM-PN-EIP(EtherNet/IP转PROFINET)网关西门子200智能PLC(PROFINET)和欧姆龙系统EtherNet/IP通信的配置过程。 1, 将 EDS 文件复制到欧姆龙软件的对应文件夹下 2, 首先添加捷米特JM-PN-EIP网关的全局变量&…...
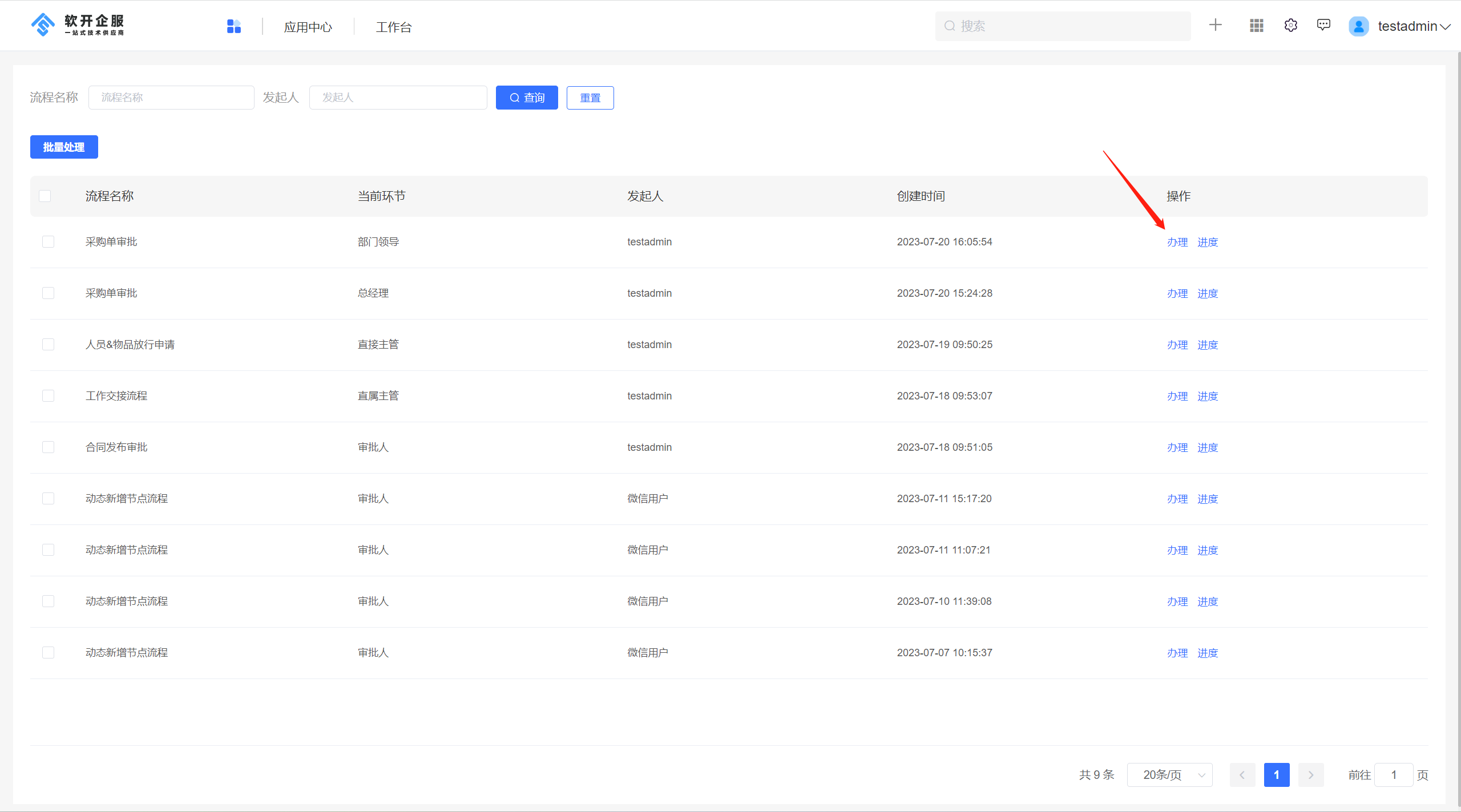
低代码开发重要工具:jvs-flow(流程引擎)审批功能配置说明
流程引擎场景介绍 流程引擎基于一组节点与执行界面,通过人机交互的形式自动地执行和协调各个任务和活动。它可以实现任务的分配、协作、路由和跟踪。通过流程引擎,组织能够实现业务流程的优化、标准化和自动化,提高工作效率和质量。 在企业…...

[SQL挖掘机] - GROUP BY语句
介绍: group by 是 sql 中用于对结果集进行分组的关键字。通过使用 group by,可以根据一个或多个列的值将结果集中的行分组,并对每个分组应用某种聚合函数(如 count、sum、avg 等)以生成汇总信息。这样可以方便地对数据进行分类、…...

【ubuntu|内核】ubuntu 22.04修改内核为指定版本
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 ubuntu 22.04 安装指定内核 1. 正文 查看已安装的内核镜像 dpkg --get-selections | grep linux-image1.1 安装指定版本的内核 安装镜像 sudo apt-g…...
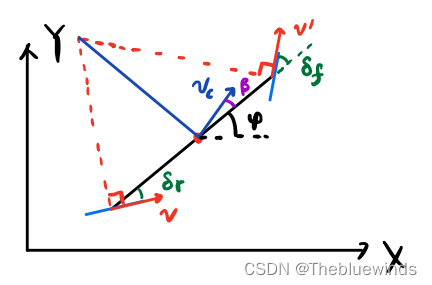
Carla教程一:动力学模型到LQR
Carla教程一、动力学模型到LQR 从运动学模型和动力学模型到LQR 模型就是可以描述车辆运动规律的模型。车辆建模都是基于自行车模型的设定,也就是将四个轮子抽象为自行车一样的两个轮子来建模。 1、运动学模型 运动学模型是基于几何关系分析出来的,一般适用于低俗情况下,…...
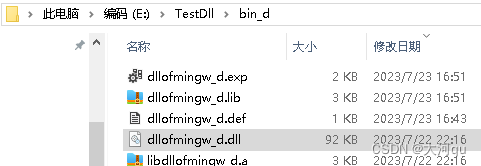
IDE/mingw下动态库(.dll和.a文件)的生成和部署使用(对比MSVC下.dll和.lib)
文章目录 概述问题的产生基于mingw的DLL动态库基于mingw的EXE可执行程序Makefile文件中使用Qt库的\*.a文件mingw下的*.a 文件 和 *.dll 到底谁起作用小插曲 mingw 生成的 \*.a文件到底是什么为啥mingw的dll可用以编译链接过程转换为lib引导文件 概述 本文介绍了 QtCreator mi…...
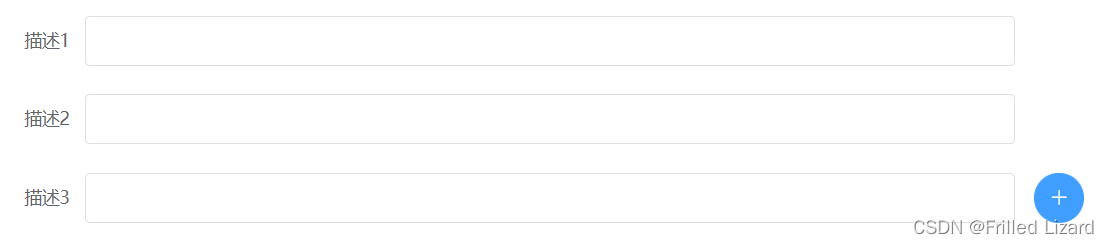
点击加号添加新的输入框
实现如上图的效果 html部分: <el-form-item class"forminput" v-for"(item,index) in formdata.description" :key"index" :label"描述(index1)" prop"description"><el-input v-model"formdata…...
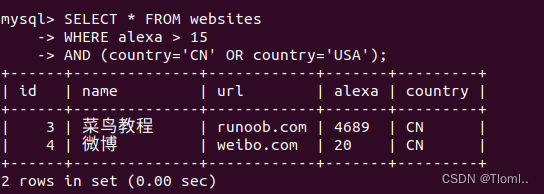
SQL AND OR 运算符
AND & OR 运算符用于基于一个以上的条件对记录进行过滤。 如果第一个条件和第二个条件都成立,则 AND 运算符显示一条记录。 如果第一个条件和第二个条件中只要有一个成立,则 OR 运算符显示一条记录。 下面是选自 "students" 表的数据&a…...

6、C++内存模型
原文: https://my.oschina.net/u/2516597/blog/805489 背景 C11开始支持多线程,其中提供了原子类型atomic, 和atomic关系比较密切的是memory_order,所有的内存模型都是指atomic类型 enum memory_order {memory_order_relaxed,memory_order…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
