【数据结构】实验二:顺序表
实验二 顺序表
一、实验目的与要求
1)熟悉顺序表的类型定义;
2)熟悉顺序表的基本操作;
3)灵活应用顺序表解决具体应用问题。
二、实验内容
1)在一个整数序列a1,a2,…,an中,若存在一个数,大于它的整数数量和小于它的整数数量相等,则该数被称为“中间数”。请编写程序实现整数序列的“中间数”测试。具体样例:
/*样例输入 5 //包含5个整数的序列
3 4 6 6 7 //随机产生一个整数序列
则输出
-1 //输出-1表示整数序列“3 4 6 6 7”中不存在中间数
说明:
①在一个整数序列中,可能存在多个中间数。
②整数序列在程序中由随机数生成,程序输出“中间数”的值,若中间数不存在,则输出-1。
2)股票收益:假设你知道接下来n天的某只股票的价格序列a1,a2,…,an,请编写程序实现确定最优的买入时间和卖出时间以获得最大收益。股票价格数组在程序中由随机数组成,程序输出最终可以获得的最大收益和买入卖出时间,若无收益则输出0。
三、实验结果
1)简述算法步骤:
2)分析算法时间复杂度:
实验内容1:
0)代码内容:
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <time.h>
using namespace std;int main(){//初始化array int n;cout<<"请输入序列所包含的个数:"; cin>>n;int arr[n];int i=0;
// for(i=0;i<n;i++){
// arr[i]=rand()%100;//假设随机生成为100以内的数字
// }
// //check array
// cout<<endl<<"随机生成的整数数组如下:"<<endl;
// for(i=0;i<n;i++){
// cout<<arr[i]<<endl;
// }//srand优于rand随机生成? int *p;srand(time(0));for(p=arr;p<(arr+n);p++){*p=rand()%100;//假设随机生成为100以内的数字 }//check arraycout<<endl<<"随机生成的整数数组如下:"<<endl; for(p=arr;p<(arr+n);p++){cout<<*p<<" ";}//遍历寻找中间数int big,small,j;//big->比当前数大的个数,small->比当前数小的个数 int temp[n],cnt=0;//暂存中间数的数组 for(i=0;i<n;i++){big=0;//初始化big small=0;//初始化small for(j=0;j<n;j++){if(arr[i]>arr[j]){big++;}else if(arr[i]<arr[j]){small++;}}if(small==big){//符合中间数的要求->判断是否为重复元素 if(cnt==0){temp[cnt]=arr[i];//首个元素 cnt++;}else{int t=0,flag=1;for(t=0;t<cnt;t++){if(arr[i]==temp[t]){flag=0;//重复元素,不计入temp数组 break;}}if(flag==1){temp[cnt]=arr[i];//非重复元素,计入temp数组 cnt++;}}}} // //check cnt
// cout<<endl<<cnt<<endl;//输出中间数cout<<endl;if(cnt==0){cout<<-1<<endl;//中间数不存在 }else{cout<<"中间数如下:"<<endl; for(i=0;i<cnt;i++){cout<<temp[i]<<endl;} }return 0;
}
1)简述算法步骤:
-->程序开始
-->利用srand函数随机生成数组元素
-->通过内外层循环遍历寻找中间数(以当前数为基准,遍历比较其他数字)
-->若序列有中间数,判断中间数是否重复(建立临时数组存放并比较)
-->输出序列中间数的情况(不存在中间数 / 所有的中间数)
-->程序结束
2)分析算法时间复杂度:
首先,我们在遍历寻找中间数的时候使用了内外层循环,即先通过外层循环假设arr数组中每一个元素均可以作为中间数进行遍历,再通过内层循环比较当前元素与其他剩余元素的大小,确定比当前元素大的个数及比当前元素小的个数,进而确定当前元素作为数组序列的中间数是否可行。所以,这段算法的时间复杂度为平方阶O(n²)。
其次,我们在判断所有中间数是否有重复情况时,建立了临时数组存放既往已经判断过的可行且不重复元素。那么,我们在下一次遇到可行的中间数元素的时候,在temp数组里面遍历与已经存入的中间数元素进行比较,确定当前元素的重复性。所以,这段算法的时间复杂度为线性阶O(n)。
3)程序运行结果示例:
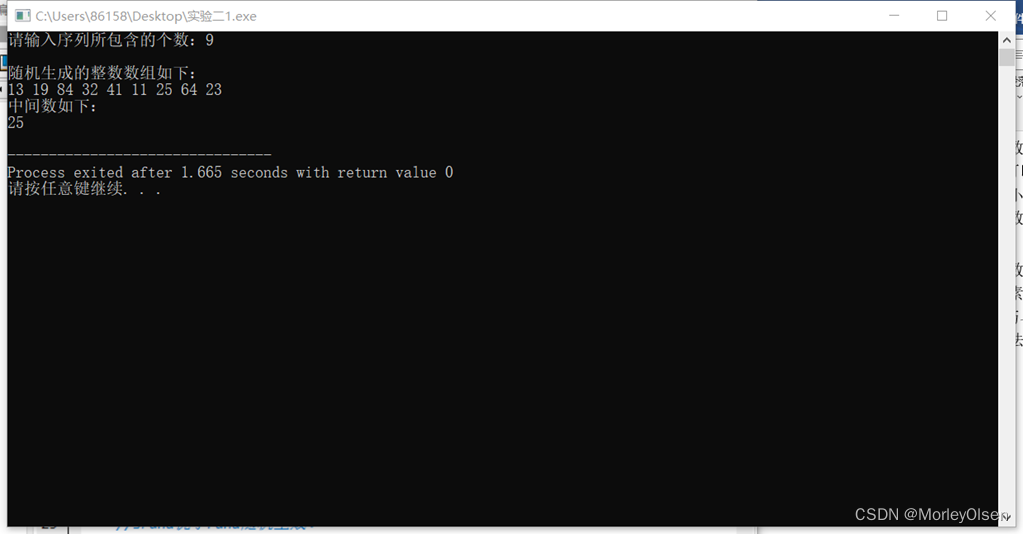
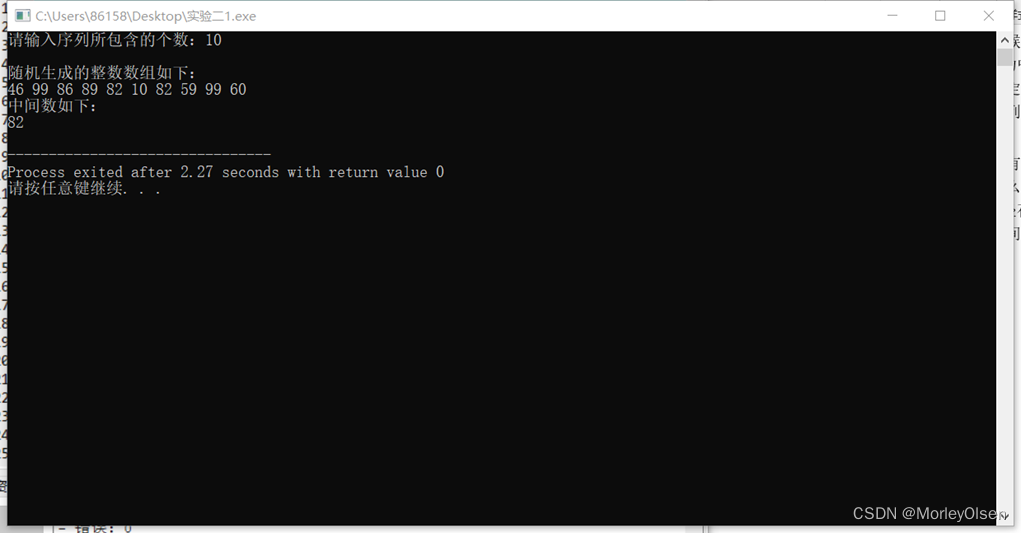
实验内容2:
0)代码内容:
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <time.h>
using namespace std;int main(){cout<<"请输入某只股票的价格序列的模拟天数:";int n,i,j;cin>>n; //随机生成价格 int price[n-1];//n天的价格 天数为i+1 int *p;srand(time(0));for(p=price;p<(price+n);p++){*p=rand()%100;//假设随机生成为100以内的数字 }//check price[]cout<<endl<<"随机生成的价格数组如下:"<<endl; for(p=price;p<(price+n);p++){cout<<*p<<" ";}cout<<endl;int cnt=0,myday[n-1],money[n-1],maxday=0;for(i=0;i<n-1;i++){maxday=i+1;//从当前开始计算利润 for(j=i+1;j<=n-1;j++){if(price[j]-price[i]>price[maxday]-price[i]){maxday=j;}}myday[cnt]=maxday;money[cnt]=price[maxday]-price[i];cnt++;}// //check myday and money
// for(i=0;i<cnt;i++){
// cout<<myday[i]+1<<","<<money[i]<<endl;
// }//最优买入时间int best=0; for(i=1;i<cnt;i++){if(money[i]>money[best]){best=i;}} //cout<<best<<endl;//输出最大收益、买入卖出时间if(money[best]<0){cout<<0<<endl;//no benefit} else{cout<<"最大收益为:"<<money[best]<<endl;cout<<"买入时间为:第"<<best+1<<"天"<<endl;cout<<"卖出时间为:第"<<myday[best]+1<<"天"<<endl;}return 0;
}1)简述算法步骤:
-->程序开始
-->利用srand函数随机生成数组元素,作为接下来几天该只股票的价格
-->通过内外层循环遍历寻找当前天数时买入后可获得的最优价格及卖出天数(以当前天数的价格为基准,遍历后续几天的价格并作差比较)
-->通过循环遍历并比较每个天数买入后的最优价格,获取最优买入时间
-->输出序列的最大收益、买入时间、卖出时间等情况
-->程序结束
2)分析算法时间复杂度:
首先,我们在遍历寻找当前天数时买入后可获得的最优价格及卖出天数的时候,使用了内外层循环。先通过外层循环确立当前天数并初始化下一次的天数的股票价格为最优卖出天数,再通过内层循环比较后面每一天与当前天数的股票价格差值,确定当前天数的最优价格和卖出天数,并分别存入money数组与myday数组之中。所以,这段算法的时间复杂度为平方阶O(n²)。
其次,我们在通过循环遍历并比较每个天数买入后的最优价格,获取最优买入时间的时候,是寻找一阶线性数组的最值的过程,即通过遍历money数组寻找最优解,并锁定myday数组里面的对应值。所以,这段算法的时间复杂度为线性阶O(n)。
3)程序运行结果示例:
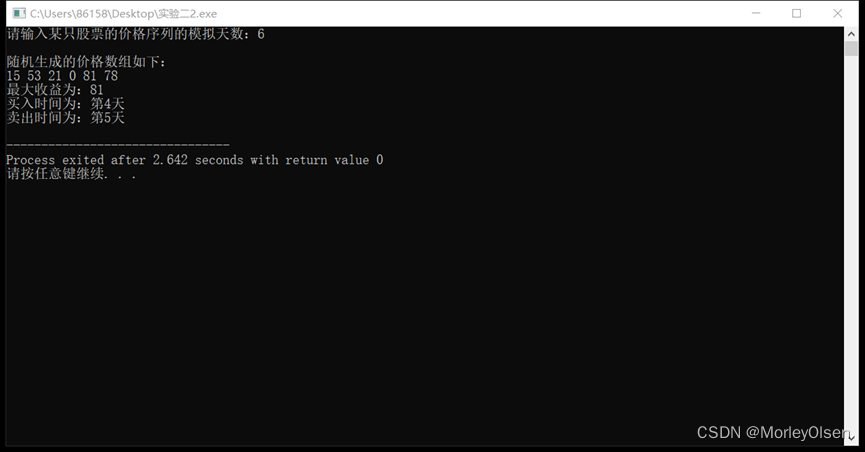
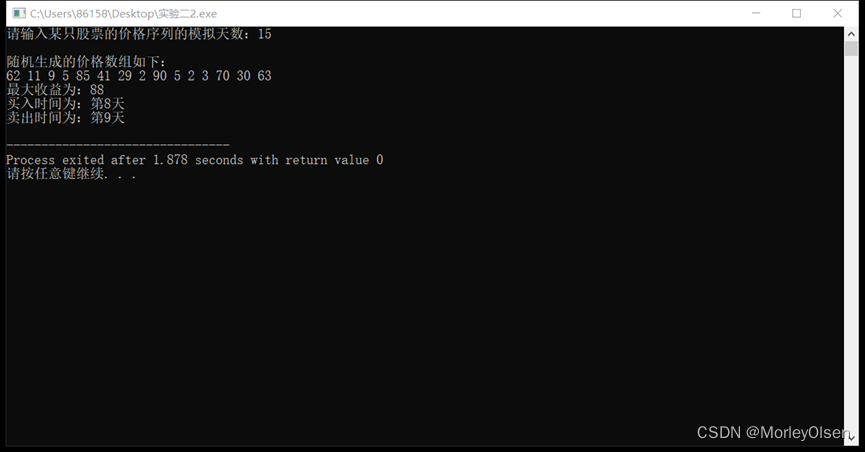
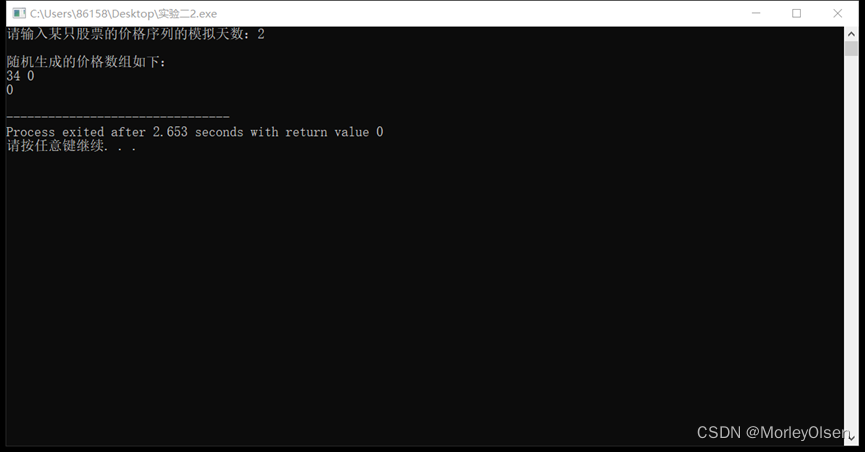
其他参考代码:
#include <iostream>
#include <cmath>
using namespace std;
int n,i;
class Sqlist{public:Sqlist()//初始化顺序表{data= new int[n];length=0;}~Sqlist()//删除顺序表{delete [] data;}void getSqlist(int m)//创建顺序表{int max=10;int min=0;for(int i=0;i<m;i++){data[i]=rand()%(max-min+1);}}void seekmiddle()//寻找中间数并输出“中间数”的值,若中间数不存在,则输出-1。{int j=0;for(;j<n;j++)//外层循环,锁定一个被比较的数data[j]{int g=0,l=0;//定义较大数(greater)的个数、较小数(less)的个数;for(i=0;i<n;i++)//内层循环,依次比较除data[j]本身的其他的数。{if(i!=j){if(data[i]>data[j]) g++;if(data[i]<data[j]) l++;}}if(g==l)//如果较大数=较小数,输出中间数{cout<<data[j];break;}}if(j==n) cout<<-1;}void printlist()//打印顺序表{for(i=0;i<n;i++)cout<<data[i]<<' ';cout<<endl;}int getlength()//返回顺序表长度{return length;}bool isEmpty()//判断顺序表是否为空;若为空,返回0{if(length==0) return false;}private:int *data;//顺序表的元素int length;//顺序表的长度
};
int main()
{Sqlist list1;cin>>n;list1.getSqlist(n);//获得随机数列list1.printlist();//打印顺序表list1.seekmiddle();//寻找并输出中间数return 0;}
#include <iostream>
#include <cmath>
using namespace std;
int n,i;
class Sqlist{public:Sqlist(){data= new int[n];length=0;}~Sqlist(){delete [] data;}void getSqlist(int m){int max=50;int min=0;for(int i=0;i<m;i++){data[i]=rand()%(max-min+1);}}void seekmax(){int max=0;int index1,index2;//记录下标,对应最佳买入、卖出的天数for(int j=0;j<n-1;j++)//外层循环,锁定第j+1天,以便比较和后面天数的差值{for(int k=j+1;k<n;k++)//内层循环,计算第j+1天和之后(第k+1天)的股票的差值{if(data[k]-data[j]>max)//依次寻找最大的差值{max=data[k]-data[j];index1=j;//记录对应下标index2=k;}}}if(max!=0){cout<<"在第"<<index1+1<<"天买入,第"<<index2+1<<"天卖出最合适。"<<endl;cout<<"最大利益为"<<max;}else cout<<0;//最大利益为0,则输出0}void printlist()//打印顺序表{for(i=0;i<n;i++)cout<<data[i]<<' ';cout<<endl;}int getlength()//返回顺序表长度{return length;}bool isEmpty()//判断顺序表是否为空;若为空,返回0{if(length==0) return false;}private:int *data;//顺序表的元素int length;//顺序表的长度
};
int main()
{Sqlist list1;cin>>n;//输入预测的天数nlist1.getSqlist(n);//获取股票list1.printlist();//打印股票list1.seekmax();//寻找最大利益return 0;
}相关文章:

【数据结构】实验二:顺序表
实验二 顺序表 一、实验目的与要求 1)熟悉顺序表的类型定义; 2)熟悉顺序表的基本操作; 3)灵活应用顺序表解决具体应用问题。 二、实验内容 1)在一个整数序列a1,a2,…,an中,若存在一个数&…...
【高级数据结构】线段树
目录 最大数(单点修改,区间查询) 线段树1(区间修改,区间查询) 最大数(单点修改,区间查询) 洛谷:最大数https://www.luogu.com.cn/problem/P1198 题目描述 …...
qt简易闹钟
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);ui->stopBtn->setDisabled(true);this->setFixedSize(this->size()); //设置固定大小this->s…...

python和c加加有什么区别,c和c++和python先学哪个
本篇文章给大家谈谈c加加编程和python编程有什么区别,以及python和c加加有什么区别,希望对各位有所帮助,不要忘了收藏本站喔。 1、python和c学哪个好 学C好。 C通常比Python更快,因为C是一种编译型语言,而Python则是…...
Visual Studio 2022 cmake配置opencv开发环境
1. 环境与说明 这里我用的是 widnows 10 64位,Visual Studio 用的 Visual Studio Community 2022 (社区版) 对于Android开发工程师来说,为什么要使用Visual Studio 呢 ? 因为在Visual Studio中开发调试OpenCV方便,可以开发调试好后…...
C++ GDAL找出多时相遥感影像缺失的日期并自动生成新的全零图像作为替补
本文介绍基于C 语言的GDAL库,基于一个存储大量遥感影像的文件夹,依据每一景遥感影像的文件名中表示日期的那个字段,找出这些遥感影像中缺失的成像日期,并新生成多个像元值全部为0的栅格文件,作为这些缺失日期当日的遥感…...

【AI底层逻辑】——篇章5(下):机器学习算法之聚类降维时间序列
续上: 目录 4、聚类 5、降维 6、时间序列 三、无完美算法 往期精彩: 4、聚类 聚类即把相似的东西归在一起,与分类不同的是,聚类要处理的是没有标签的数据集,它根据样本数据的分布特性自动进行归类。 人在认知是…...

P1980 [NOIP2013 普及组] 计数问题
[NOIP2013 普及组] 计数问题 题目描述 试计算在区间 1 1 1 到 n n n 的所有整数中,数字 x x x( 0 ≤ x ≤ 9 0\le x\le9 0≤x≤9)共出现了多少次?例如,在 1 1 1 到 11 11 11 中,即在 1 , 2 , 3 , 4…...
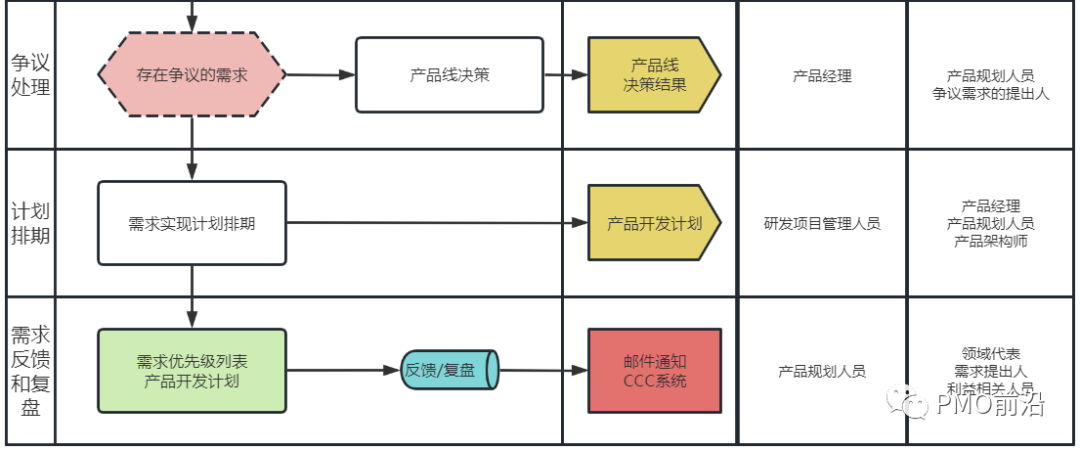
需求管理全过程流程图及各阶段核心关注点详解
分析报告指出,多达76%的项目失败是因为差劲的需求管理,这个是项目失败的最主要原因,比落后的技术、进度失控或者混乱的变更管理还要关键。很多项目往往在开始的时候已经决定了失败,谜底就在谜面上,开始就注定的失败&am…...

Android开源 自定义emoji键盘,EmojiPack v2.1版本
目录 一,简介 二、安装 添加jitpack 仓库 添加依赖: 混淆规则: 三、使用 1、一次性配置emoji显示处理 二、emoji的自定义键盘的使用 一,简介 EmojiPack当前已提供emoji的显示和emoji的选择自定义键盘,在emoji显示这一方面࿰…...

SOLIDWORKS软件的优势分析 硕迪科技
在现代的机械设计领域,SOLIDWORKS是一款备受青睐三维设计软件,它具备强大的建模和设计功能,在全球范围内广泛应用于机械设计和工程领域,为用户提供了全面的工程解决方案。本文就SOLIDWORKS的优势进行详细分析。 1、易于学习和使用…...
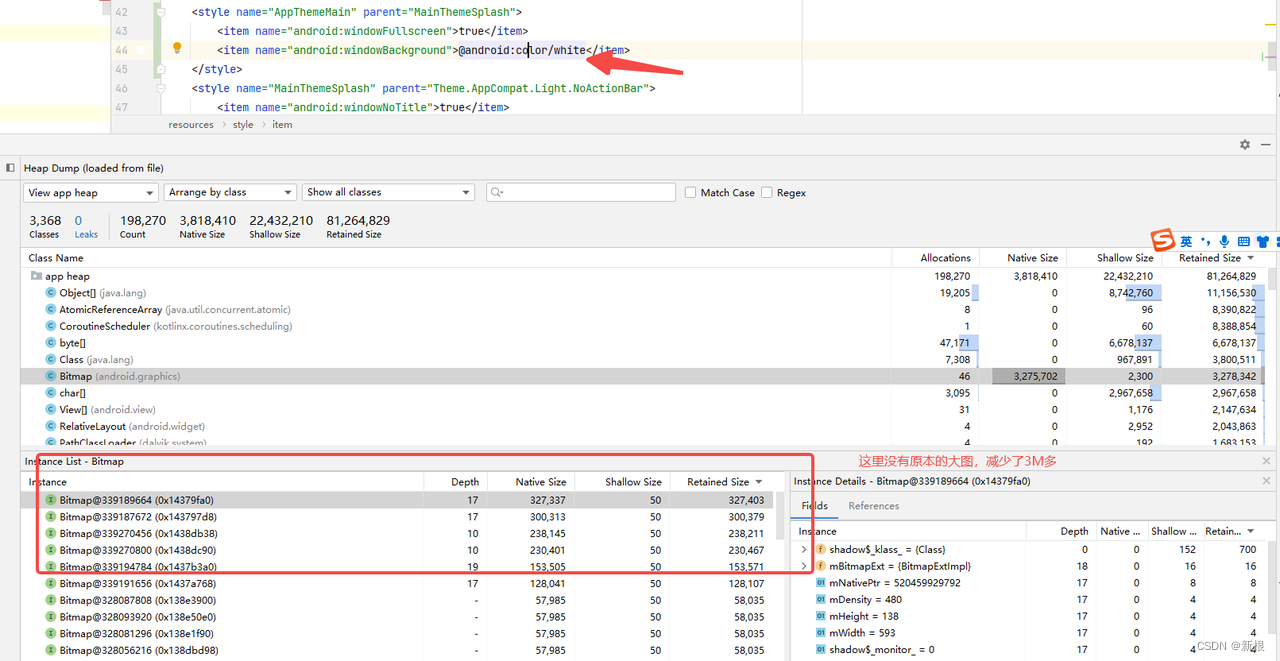
Android性能优化之游戏的Theme背景图
近期,对游戏的内存优化,通过内存快照发现,某个Activity的theme背景图 占用3M 多。考虑着手对齐进行优化。 问题 查看游戏中的内存快照,发现有一个图片bitmap 占用3M 多,设置在Activity的背景中: 查看Phon…...

网络安全(黑客)系统自学,成为一名白帽黑客
前言 黑客技能是一项非常复杂和专业的技能,需要广泛的计算机知识和网络安全知识。你可以参考下面一些学习步骤,系统自学网络安全。 在学习之前,要给自己定一个目标或者思考一下要达到一个什么样的水平,是学完找工作(…...

lua学习-2 常见运算符
文章目录 赋值运算符普通赋值多重赋值交换赋值 算数运算符常见符号标识 关系运算符常见符号标识TIP 逻辑运算符常见符号标识模拟三目运算 赋值运算符 普通赋值 a 1b "123"c truec "true"多重赋值 a,b 1,2 a,b,c 2,"ss" -- c的值为nil交换赋…...

【图像处理】使用 OpenCV 将您的照片变成卡通
图像到卡通 一、说明 在当今世界,我们被图像和视频所包围。从社交媒体到广告,图像已成为一种强大的交流媒介。但是你有没有想过,如果你能把你的照片变成卡通会发生什么?想象一下,为您最喜欢的照片创建动画版本…...

暖手宝UL认证 亚马逊UL测试报告 UL499测试项目
UL499测试内容:1、 漏电流测试 2、 输入测试 3、 潮态下漏电流测试4、正常温升测试 5、 耐高压测试 6、 稳定性测试7、异常测试(DRY)8、 异常测试 9、 静压及强度测试10、 烧熔断器测试、 电源线拉力测试11、 电源线推力测试12、 塑件变…...

ES6模块化与异步编程高级用法
1. ES6模块化 1.1 回顾:node.js 中如何实现模块化 node.js 遵循了 CommonJS 的模块化规范。其中: 导入其它模块使用 require() 方法模块对外共享成员使用 module.exports 对象 模块化的好处: 大家都遵守同样的模块化规范写代码࿰…...

spring-cloud-starter-gateway 4.0.6负载均衡失败
spring:application:name: gatewaycloud:gateway:routes:- id: memberuri: lb://memberpredicates:- Path/member/**需要引入下面负载均衡依赖否则503找不到服务 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-s…...

Tomcat注册为Windows服务
要将Tomcat注册为Windows服务,可以使用Tomcat提供的实用工具service.bat。以下是注册和配置Tomcat作为Windows服务的步骤: 打开命令提示符(Command Prompt)或 PowerShell,然后进入Tomcat安装目录的"bin"文件…...

【Maven】Maven 中 pom.xml 文件
文章目录 前言什么是 pom?pom配置一览 1. dependencies2.scope3.properties4.plugin参考 前言 Maven 是一个项目管理工具,可以对 Java 项目进行构建和管理依赖。 本文,我们认识下 pom.xml 文件。POM(Project Object Model, 项目…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
