Linux chmod
chmod
首先chmod 用于修改文件权限,使用命令 ll 查看文件列表,或者使用stat+文件名 可以查看其相应的权限 显示的形式为例如 rwx r- - r-- ,即所有者拥有读写执行的权限 ,同组人员和其他人都只拥有读的权限
一般修改权限为三部分 命令 + 权限码 + 文件名
-
命令为 chmod
-
权限代码 一般为三个数字 如 777 444 等。
-
每组数字有三个 每个数字分别为 1 2 4 这三个数字的任意个数 数字的和 比如 7 就是 1 + 2 + 4,5 就是 1 + 4, 4 就是 4
-
具体意义 1 2 4 对应的分别是二进制中的 001 010 100,其对应的权限分别为 r _ _(读 )
_ w _(写) _ _ x (执行)读写权限就是 110 rw _ 5
-
三个数字分别代表所有者 同组人 其他用户 的权限
-
-
eg: 比如一个文件原来的权限为 rwx r- - r-- ,即所有者拥有读写执行的权限 ,其他人都只有读的权限,现在要撤销所有者的写权限
-
chmod 544 文件名
相关文章:

Linux chmod
chmod 首先chmod 用于修改文件权限,使用命令 ll 查看文件列表,或者使用stat文件名 可以查看其相应的权限 显示的形式为例如 rwx r- - r-- ,即所有者拥有读写执行的权限 ,同组人员和其他人都只拥有读的权限 一般修改权限为三部分…...

java商城系统和php商城系统有什么差异?如何选择?
java商城系统和php商城系统是两种常见的电子商务平台,它们都具有一定的优势和劣势。那么,java商城系统和php商城系统又有哪些差异呢? 一、开发难度 Java商城系统和PHP商城系统在开发难度方面存在一定的差异。Java商城系统需要使用Java语言进…...
)
【HTML】常用实体字符(如 nbsp; 空格)
文章目录 显示结果描述实体名称实体编号空格 <小于号<<>大于号>>&和号&"引号" ’撇号' (IE不支持)¢分(cent)¢¢£镑(pound)£ £元&…...
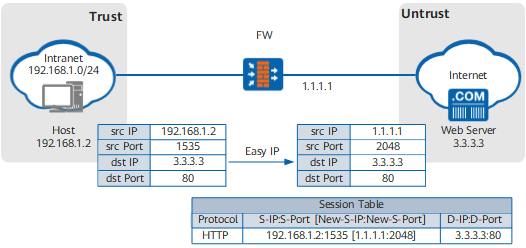
华为eNSP通过VMnet8虚拟网卡,NAT转换访问互联网
防火墙上配置: 配置G1/0/1接口IP地址,其实G1/0/1的IP就是终端PC1的网关地址。 配置G1/0/0接口自动获取IP地址,从VMnet8中自动获取地址。 配置安全区域zone,把对应的接口加入到对应的zone中 配置安全策略,放通trust安全区域到u…...

手撕顺序表
> 作者简介:დ旧言~,目前大一,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 望小伙伴们点赞👍收藏✨加关注哟💕…...

Python实战项目——旅游数据分析(四)
由于有之前的项目,所以今天我们直接开始,不做需求分析,还不会需求分析的可以看我之前的文章。Python实战项目——用户消费行为数据分析(三) 导入库 import numpy as np import pandas as pd import matplotlib.pyplo…...
)
前端CryptoJS-AES加解密 对应php的AES-128-CBC加解密踩坑(java也相同加解密)
前端部分注意看填充是pkcs7 有个前提,要看前端有没有转成hex格式,如果没转,php那边就不需要调用特定函数转hex格式的 const keyStr 5hOwdHxpW0GOciqZ;const iv 0102030405060708;//加密function Encrypt(word) {let key CryptoJS.enc.Ut…...

Python解码张三的法外狂徒之旅,揭秘视频背后的真相!【含jS逆向解密】
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 传说中,有人因为只是远远的看了一眼法外狂徒张三就进去了😂 我现在是获取他视频,岂不是直接终生了🤩 网友:赶紧跑路吧 😏 好了话不多说ÿ…...

【解析】对比学习和孪生网络的关系
文章目录 区别联系具体概念孪生网络(Siamese Networks)对比学习(Contrastive Learning) 区别 孪生网络是一种特定的神经网络结构;对比学习是一种学习策略,它试图让模型学习如何区分正样本对(相…...

Java版本企业工程项目管理系统平台源码(三控:进度组织、质量安全、预算资金成本、二平台:招采、设计管理)
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&#…...

智能井盖:科技赋能城市脚下安全
在智能化飞速发展的今天,智能井盖作为城市基础设施的一部分,正逐渐走进人们的视野。它利用现代科技手段,实现了对城市井盖的实时监控、及时响应和高效管理,为城市管理、市民出行等方面带来了诸多便利。 城市中井盖数量庞大&#x…...

wangeditor编辑器配置
vue项目中使用编辑器,轻量,操作栏选取自己需要的 官网地址:用于 Vue React | wangEditor 使用在vue项目中引入 npm install wangeditor/editor --savenpm install wangeditor/editor-for-vue --save 封装成组件使用 <template>&…...

Sqlite使用WAL模式指南
本文地址:http://t.csdn.cn/kE8ND 文章目录 一、WAL模式的原理二、开启WAL后必须要设置的参数1.PRAGMA SYNCHRONOUS(1)SYNCHRONOUS的类型(2)WAL下如何选择SYNCHRONOUS类型 2.PRAGMA wal_autocheckpoint3.sqlite3_busy…...

一套高质量可靠的 React Hooks 库
个人使用,感受,挺好用 https://ahooks.js.org/zh-CN 我主要用了这个 useCountDown 倒计时,再也不用费心费力去写一个倒计时方法了,而且直接提供end之后要做什么。...
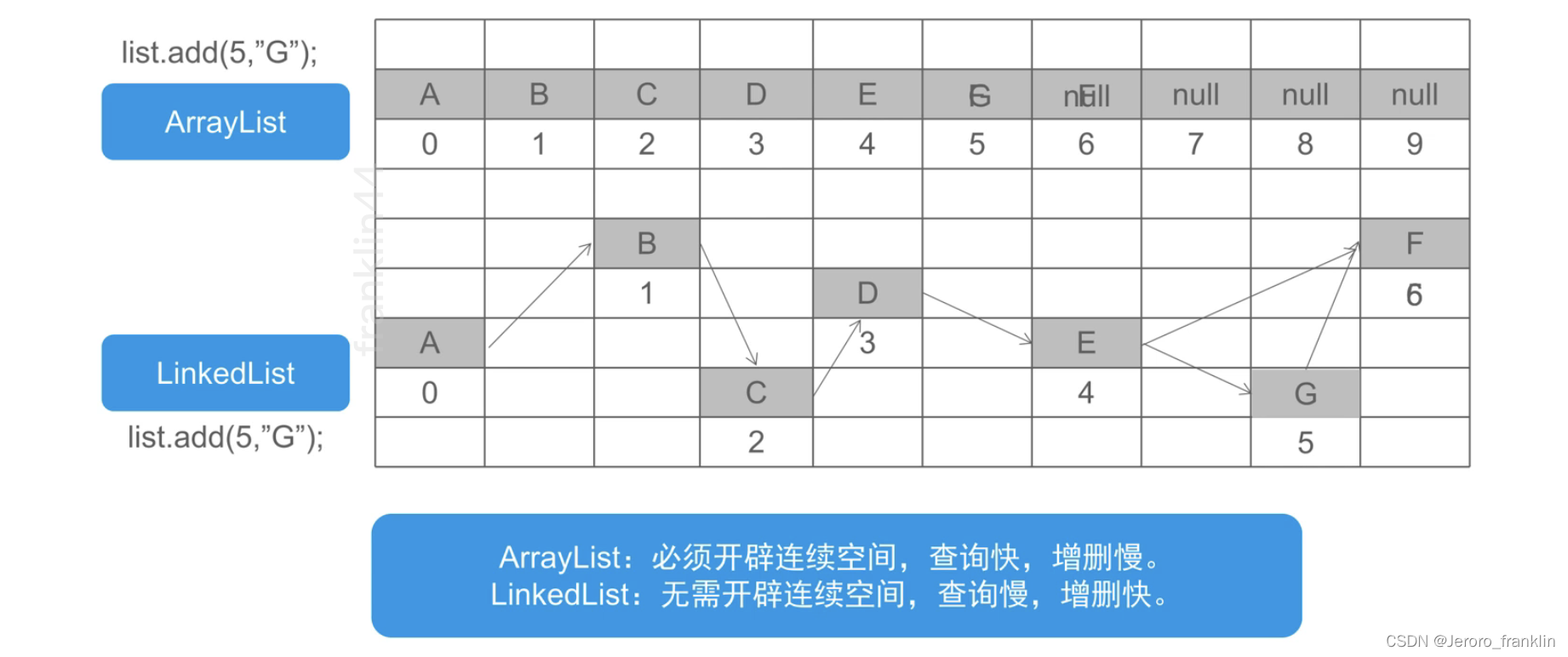
集合---list接口及实现类
一、list概述 1、list接口概述 List接口继承自Collection接口,是单列集合的一一个重要分支,我们习惯性地会将实现了 List接口的对象称为List集合。在List集合中允许出现重复的元素,所有的元素是以一种线性方 式进行有序存储的,在…...
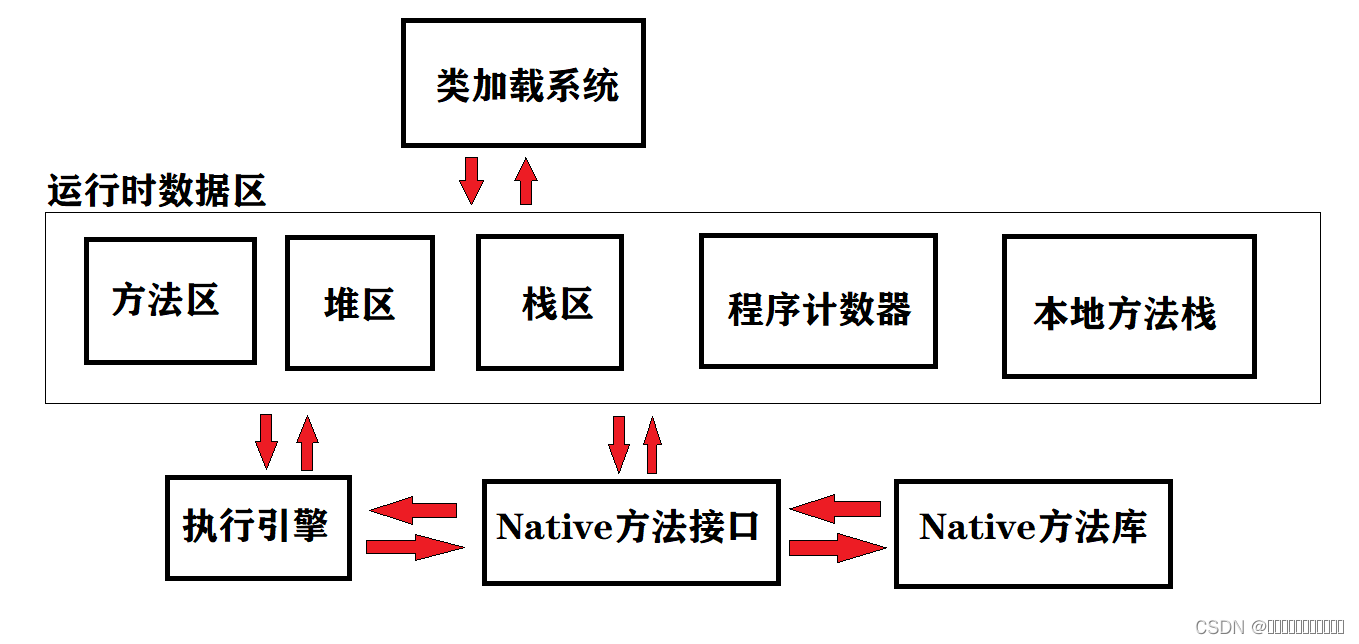
JVM简述
JDK&JRE&JVMJVM运行时内存结构图方法区堆区栈区程序计数器本地方法栈 JVM 的主要组成部分及其作用 JDK&JRE&JVM JVM就是java虚拟机,一台虚拟的机器,用来运行java代码 但并不是只有这台机器就可以的,java程序在运行时需要依赖…...

7.25训练总结
考场错误: A题其实并不简单,但是先想了一个方法后,就交了,wa了后一直卡住,策略不当,到最后后期写C的时候也犯了一些低级的错误,这点需要注意。 之后顺利的把BCDHI写完后,又完成了A的…...
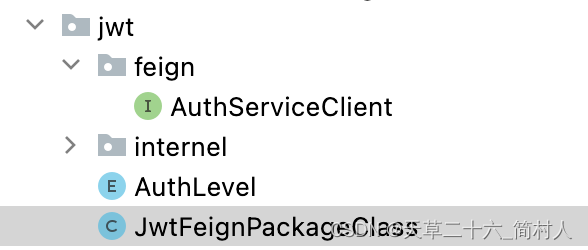
java注解@FeignClient修饰的类路径不在spring boot入口类所在的包下,有哪几种处理方式?
一、注解EnableFeignClients 修饰在spring boot入口类,使得openfeign的FeignClient注解生效。 我们进一步看看注解EnableFeignClients的使用方式。 String[] basePackages() default {};Class<?>[] basePackageClasses() default {};Class<?>[] clie…...

神经网络随记-参数矩阵、剪枝、模型压缩、大小匹配、、
神经网络的参数矩阵 在神经网络中,参数矩阵是模型学习的关键部分,它包含了神经网络的权重和偏置项。下面是神经网络中常见的参数矩阵: 权重矩阵(Weight Matrix):权重矩阵用于线性变换操作,将输…...

4、Kubernetes 集群 YAML 文件详解
目录 一、YAML 概述 二、YAML 基本语法 三、YAML 数据结构 四、k8s资源清单描述方法 五、YAML 快速编写 1、使用 kubectl create 命令 2、使用 kubectl get 命令导出 yaml 文件 一、YAML 概述 k8s 集群中对资源管理和资源对象编排部署都可以通过声明YAML文件来解决&…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
