数学建模学习(5):数学建模各类题型及解题方案
一、数学建模常见的题型

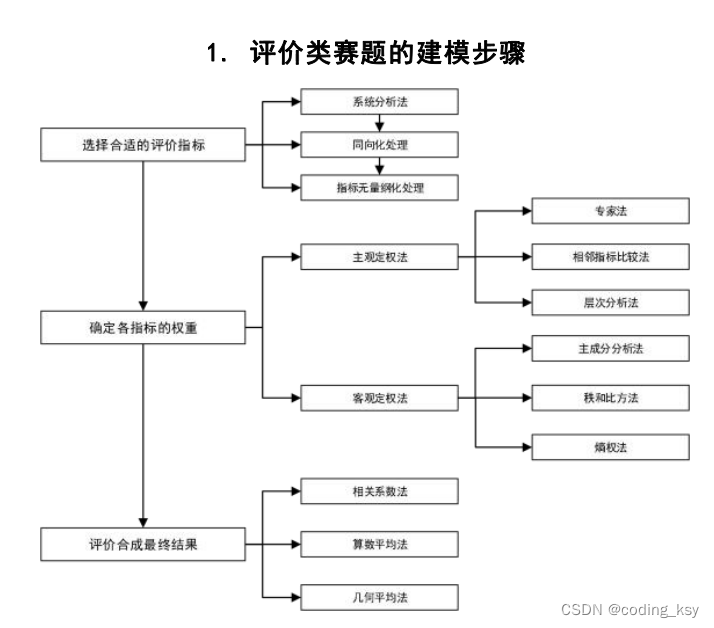
二、评价类赛题
综合评价是数学建模中的一类常见的问题,在国赛和美赛中都经常出现,例如国赛05年长江水质的综合评、2010年上海世博会影响力的定量评估问题、2014年美赛“最好大学教练“问题、2015年的“互联网+”时代的出租车资源配等都属于综合评价类问题。
综合评价是数学建模中的一类常见的问题,在国赛和美赛中都经常出现,例如国赛05年长江水质的综合评、2010年上海世博会影响力的定量评估问题、2014年美赛“最好大学教练“问题、2015年的“互联网+”时代的出租车资源配等都属于综合评价类问题。
2.主客观评价问题的区别
●主客观概念主要是在指标定权时来划分的。主观评价与客观评价的区别是,主观评价算法在定权时主要以判断者的主观经验为依据,而客观评价则主要基于测量数据的基本特性来综合定权
●定权带有一定的主观性,用不同方法确定的权重分配,可能不尽一致,这将导致权重分配的不确定性,最终可能导致评价结果的不确定性。因而在实际工作中,不论用哪种方法确定权重分配,都应当依赖于较为合理的专业解释。
3.如何选择合适的评价方法
●在评价类问题的分析中,如何选择合适的评价方法是决定评价结果好坏的关键因素,因此需要洞悉各常用评价方法的基本特性和使用条件才能顺利答题!

三、预测类赛题
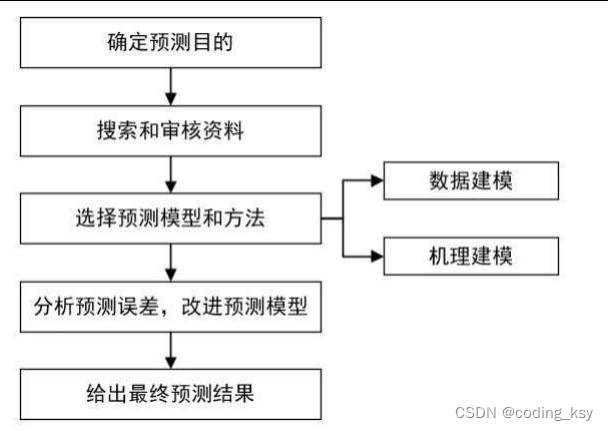
1 预测类赛题的基本解题步骤
●预测就是根据过去和现在,估计未来预测未来。统计预测属于预测方法研究范畴,即如何利用科学的统计方法对事物的未来发展进行定量推测
●基于数学建模的预测方法种类繁多,从经典的单耗法、弹性系数法、统计分析法,到目前的灰色预测法。当在使用相应的预测方法建立预测模型时,我们需要知道主要的一些预测方法的研究特点,优缺点和适用范围
2 预测类问题的区别
●预测类问题分为两类:
●一类是无法用数学语言刻画其内部演化机理的问题;
●另一类是可以通过微分方程刻画其内部规律,这类问题我们称为机理建模问题,通过微分方程建模求解。
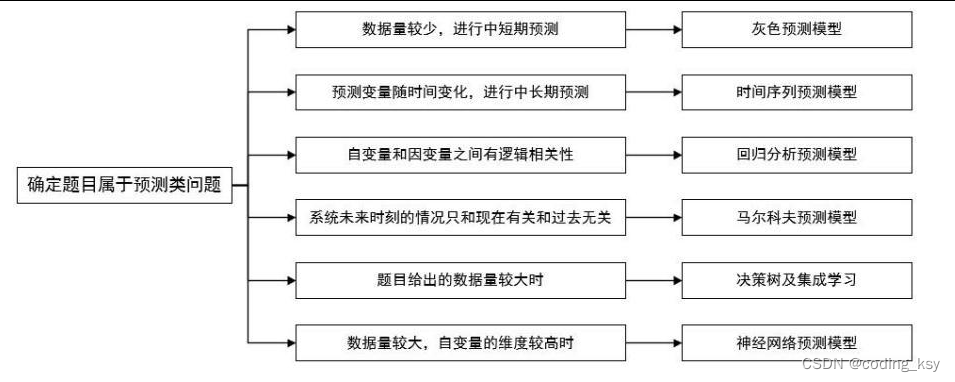
3 如何选择合适的预测方法
●在预测类问题的分析中,同样受到预测条件的限制(如数据量的大小、变量之间的关系等)不同的预测方法可能会产生不同的结果,因此需要根据实际情况来选择。
三、优化类问题
1 优化类赛题的基本解题步骤
●优化类问题是从所有可能方案中选择最合理的方案以达到最优目标。在各种科学问题、工程问题、生产管理、社会经济问题中,人们总是希望在有限的资源条件下,用尽可能小的代价,获得最大的收获(比如保险)。
●优化类问题一般的解题步骤为:
●(1)首先确定决策变量,也就是需要优化的变量;
●(2)然后确定目标函数,也就是优化的目的;
●(3)最后确定约束条件,决策变量在达到最优状态时,受到那些客观限制。

2 部分国赛优化类赛题的解决方案
●在08年国赛眼科病床的合理安排问题中,
●目标函数为医院病床的利用率最高;
·决策变量为服务策略:是先到病人先住院、急诊病人先住院还是占用病床时间短的病人先住院等;
●约束条件可能包括病人最长等待时间限制、不同症状之间的病人不同房等;
●在10年国赛交巡警服务平台的设置与调度问题中,
●决策变量为服务平台的位置坐标;
●目标函数为交巡警车到达事发地时间最短、交巡警封锁交通要道时间最短;
●约束条件可能包括事故发生后交警最晚到达时间,一定区域内服务平台最低数量要求等。
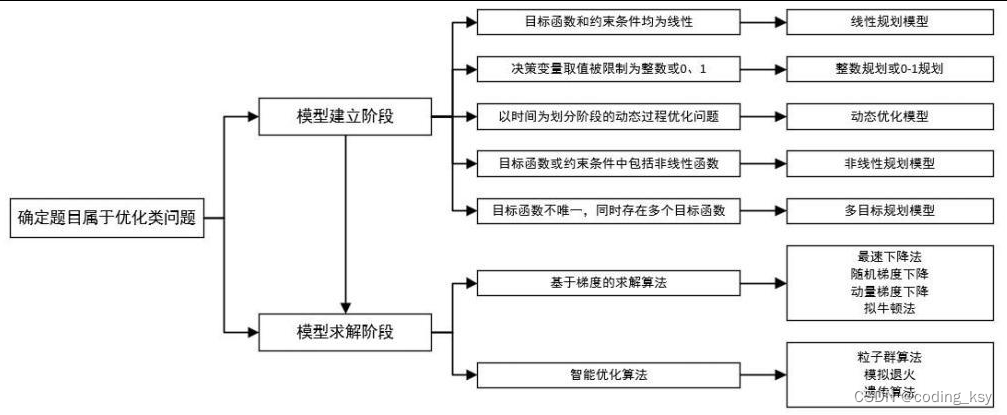
3 如何选择合适的优化方法
●优化类问题中常用的数学模型和求解算法,其中包括线性规划、非线性规划、整数规划、多目标规划等在模型求解中,对于凸优化模型,可以采用基于梯度的求解算法;对于非凸的优化模型,可以采用智能优化算法。
相关文章:

数学建模学习(5):数学建模各类题型及解题方案
一、数学建模常见的题型 总体来说,数学建模赛题类型主要分为:评价类、预测类和优化类三种,其中优化类是最常见的赛题类 型,几乎每年的地区赛或国赛美赛等均有出题,必须要掌握并且熟悉。 二、评价类赛题 综合评价是数学…...
【学习笔记】视频检测方法调研
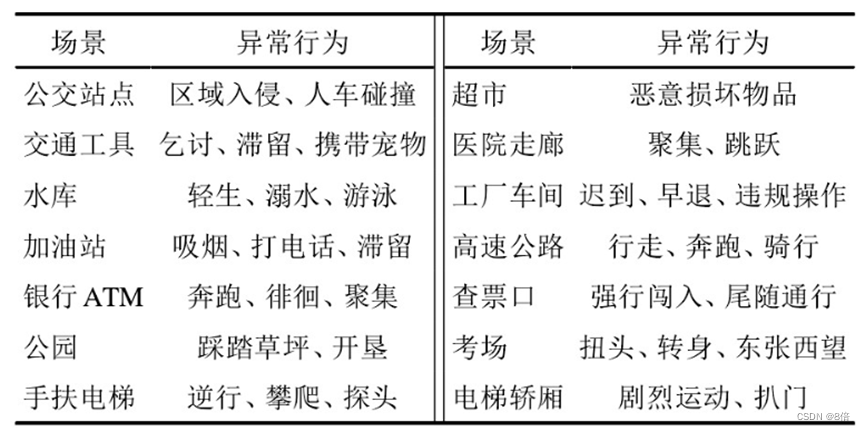
目录 1 引言2 方法2.1 视频目标跟踪2.1.1 生成式模型方法2.1.2 判别式模型方法2.1.2.1 基于相关滤波跟踪2.1.2.2 基于深度学习跟踪 2.2 视频异常检测2.2.1 基于重构方法2.2.2 基于预测方法2.2.3 基于分类方法2.2.4 基于回归方法 2.3 深度伪造人脸视频检测2.3.1 基于RNN时空融合…...
idea terminal npm指令无效
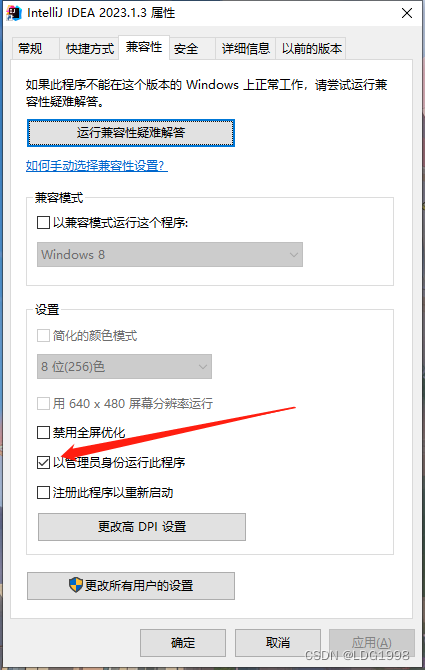
文章目录 一、修改setting二、修改启动方式 一、修改setting 菜单栏:File->Settings 二、修改启动方式 快捷方式->右键属性->兼容性->勾选管理员身份运行...
低代码开发平台源码
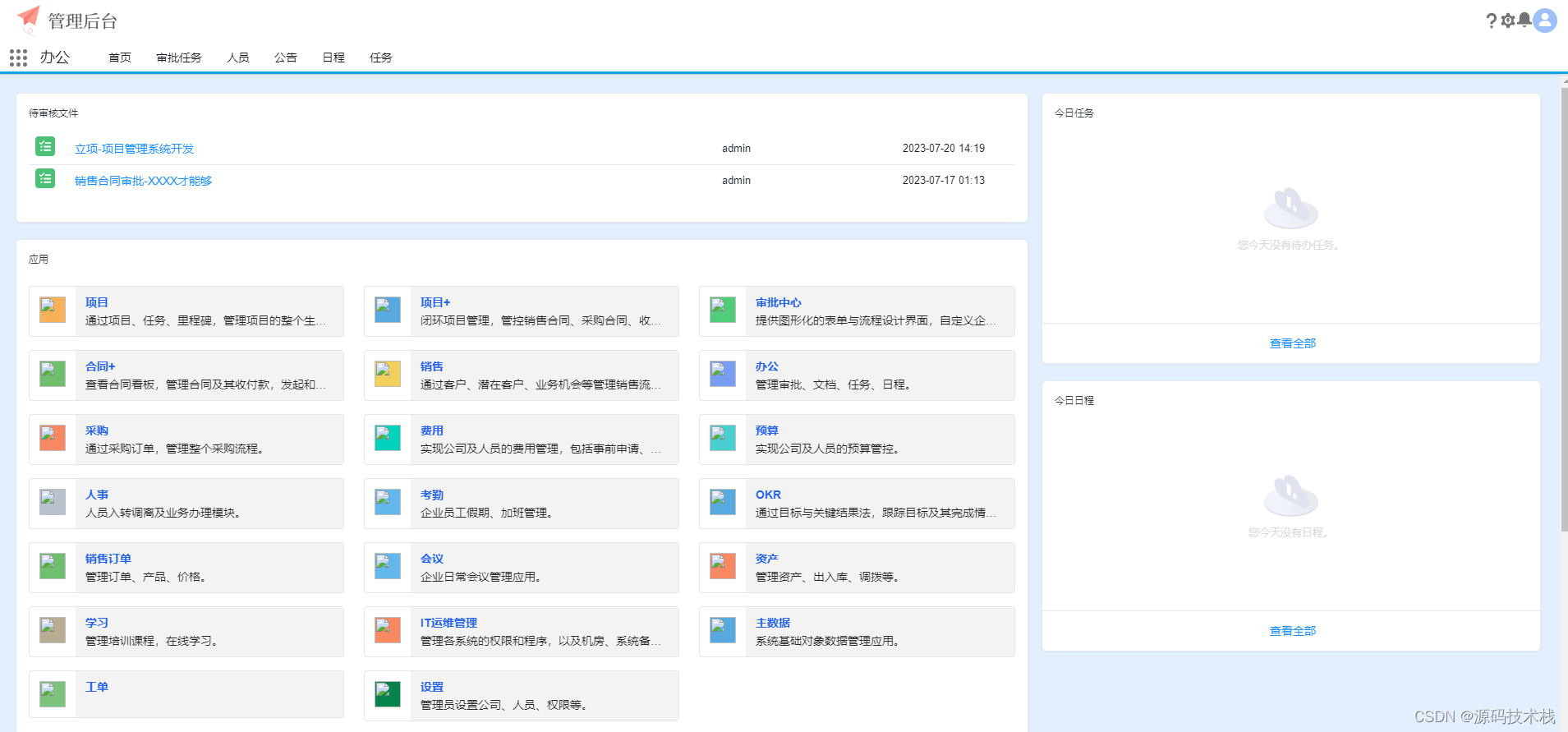
什么是低代码开发平台? 低代码来源于英文“Low Code,它意指一种快速开发的方式,使用最少的代码、以最快的速度来交付应用程序。通俗的来说,就是所需代码数量低,开发人员门槛低,操作难度低。一般采用简单的图…...
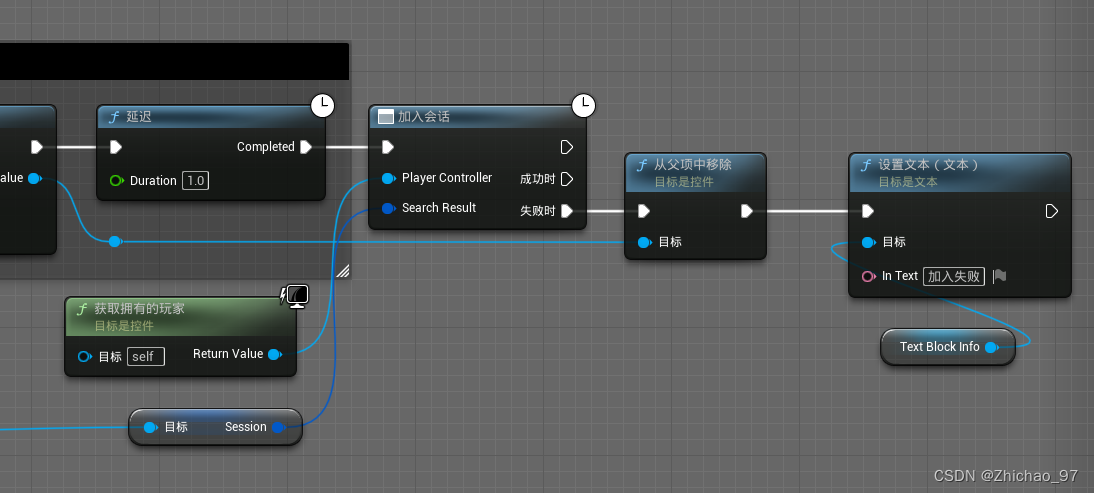
【UE5 多人联机教程】04-加入游戏
效果 步骤 1. 新建一个控件蓝图,父类为“USC_Button_Standard” 控件蓝图命名为“UMG_Item_Room”,用于表示每一个搜索到的房间的界面 打开“UMG_Item_Room”,在图表中新建一个变量,命名为“Session” 变量类型为“蓝图会话结果…...
-[大型语言模型(LLMs):缓存LLM的调用结果])
自然语言处理从入门到应用——LangChain:模型(Models)-[大型语言模型(LLMs):缓存LLM的调用结果]
分类目录:《自然语言处理从入门到应用》总目录 from langchain.llms import OpenAI在内存中缓存 import langchain from langchain.cache import InMemoryCachelangchain.llm_cache InMemoryCache()# To make the caching really obvious, lets use a slower mode…...

Python 算法基础篇之图的遍历算法:深度优先搜索和广度优先搜索
Python 算法基础篇之图的遍历算法:深度优先搜索和广度优先搜索 引言 1. 图的遍历概述2. 深度优先搜索( DFS )2.1 DFS 的实现2.2 DFS 的应用场景 3. 广度优先搜索( BFS )3.1 BFS 的实现3.2 BFS 的应用场景 4. 示例与实例…...

文本缩略 文本超出显示省略号 控制超出省略的行数
文本缩略 .abb{//超出一行省略overflow:hidden; white-space:nowrap; text-overflow:ellipsis; }超出2行省略 .abb2{display: -webkit-box !important;-webkit-box-orient: vertical;//超出2行省略-webkit-line-clamp:2;overflow: hidden; }控制超出省略的行数 .txt-over{/*控…...
云原生架构
1. 何为云原生? 很多IT业内小伙伴会经常听到这个名词,那么什么是云原生呢?云原生是在云计算环境中构建、部署和管理现代应用程序的软件方法。 当今时代,众多企业希望构建高度可扩展、灵活且有弹性的应用程序,以便能够快…...

Java 生成随机数据
文章目录 1. Java-faker依赖demo 2. common-random依赖demo 1. Java-faker 依赖 <dependency><groupId>com.github.javafaker</groupId><artifactId>javafaker</artifactId><version>1.0.2</version> </dependency>https://…...

基于OpenCV的红绿灯识别
基于OpenCV的红绿灯识别 技术背景 为了实现轻舟航天机器人实现红绿灯的识别,决定采用传统算法OpenCV视觉技术。 技术介绍 航天机器人的红绿灯识别主要基于传统计算机视觉技术,利用OpenCV算法对视频流进行处理,以获取红绿灯的状态信息。具…...

JavaScript快速入门:ComPDFKit PDF SDK 快速构建 Web端 PDF阅读器
JavaScript快速入门:ComPDFKit PDF SDK 快速构建 Web端 PDF阅读器 在当今丰富的网络环境中,处理 PDF 文档已成为企业和开发人员的必需品。ComPDFKit 是一款支持 Web 平台并且功能强大的 PDF SDK,开发人员可以利用它创建 PDF 查看器和编辑器&…...

Flutter 网络请求
在Flutter 中常见的网络请求方式有三种:HttpClient、http库、dio库; 本文简单介绍 使用dio库使用。 选择dio库的原因: dio是一个强大的Dart Http请求库,支持Restful API、FormData、拦截器、请求取消、Cookie管理、文件上传/下载…...

吃透《西瓜书》第三章 线性模型:多元线性回归
🍉 吃瓜系列 教材:《机器学习》 周志华著 🕒时间:2023/7/26 目录 一、多元线性回归 1 向量化 1.1.1 向量化 1.1.2 使用最小二乘法构建损失函数 1.1.3 去除求和符号,改成向量点乘的形式 1.1.4 数学原理 2 求解…...
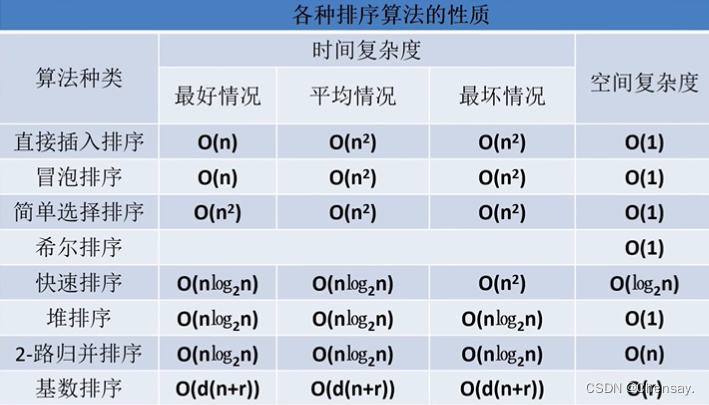
数据结构【排序】
第七章 排序 一、排序 1.定义:将无序的数排好序 ; 2.稳定性: Kᵢ和Kⱼ中,Kᵢ优先于Kⱼ那么在排序后的记录中仍然保持Kᵢ优先; 3.评价标准:执行时间和所需的辅助空间,其次是算法的稳定性…...

探索APP开发的新趋势:人工智能和大数据的力量
随着5G技术的不断发展,人工智能和大数据将会更加广泛的应用于我们生活和工作中,作为 APP开发公司,应该及时的对新技术进行研发,进而更好的为用户服务。目前 APP开发已经不是传统的软件开发了,而是向移动互联网转型&…...

超越传统:深入比较Bootstrap、Foundation、Bulma、Tailwind CSS和Semantic UI的顶级CSS框架!
探索流行的CSS框架:Bootstrap vs Foundation vs Bulma vs Tailwind CSS vs Semantic UI 在Web开发中,选择适合项目需求的CSS框架可以极大地简化界面设计和响应式布局的工作。本文将详细介绍一些流行的CSS框架,并提供代码示例和比较ÿ…...
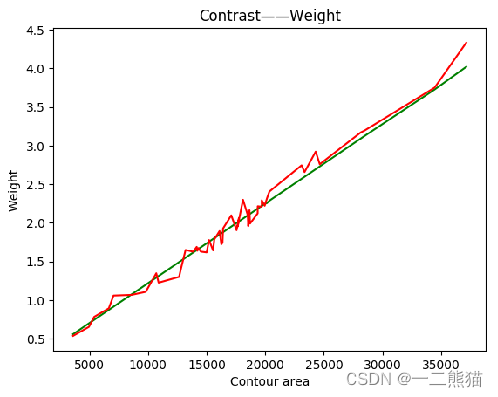
基于深度学习淡水鱼体重智能识别模型研究
工作原理为:首先对大众淡水鱼图片进行数据清洗并做标签分类,之后基于残差网络ResNet50模型进行有监督的分类识别训练,获取识别模型。其次通过搭建回归模型设计出体重模型,对每一类淡水鱼分别拟合出对应的回归方程,将获…...
--linux安装nginx)
Nginx专题(1)--linux安装nginx
ngixn安装 安装依赖包 yum install gcc yum install pcre-devel yum install zlib zlib-devel yum install openssl openssl-devel 安装nginx 下载nginx的tar包 登录http://nginx.org/en/download.html,下载nginx的Stable version版本,并解压 #执行c…...
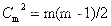
系统集成中级计算汇总
基本计算: EV 挣值 (实际完成的工作量) AC 实际发生的花费 PV 计划花费(预算) CV 成本 SV 进度 CV 和 SV 的计算 都是通过EV 减去另一个值 CV EV-AC SV EV-PV 成本 chengben C 开头 所以CV 是成本 CV 中有个C 所以用到的是 AC ,另外一个则是剩余的PV CV SV 计算…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
