【深度学习中常见的优化器总结】SGD+Adagrad+RMSprop+Adam优化算法总结及代码实现
文章目录
- 一、SGD,随机梯度下降
- 1.1、算法详解
- 1)MBSGD(Mini-batch Stochastic Gradient Descent)
- 2)动量法:momentum
- 3)NAG(Nesterov accelerated gradient)
- 4)权重衰减项(weight_decay)
- 5)总结
- 1.2、Pytorch实现:torch.optim.SGD
- 1.3、示例
- 二、Adagrad:自适应梯度
- 2.1、算法详解
- 2.2、Pytorch的实现:torch.optim.Adagrad
- 三、RMSprop
- 3.1、算法详解
- 3.2、Pytorch的实现:torch.optim.RMSprop
- 四、Adam
- 4.1、算法详解
- 4.2、Pytorch的实现:torch.optim.Adam
- 这个博客讲的非常清晰:https://blog.csdn.net/xian0710830114/article/details/126551268
一、SGD,随机梯度下降
1.1、算法详解
1)MBSGD(Mini-batch Stochastic Gradient Descent)
- 随机梯度下降其实可以有三种实现方式,最为常用,而且在pytorch中实现的也是小批量随机梯度下降。
- 有以下三种:
1)BGD(批量梯度下降法):每次迭代使用全部训练样本来计算梯度,并根据梯度的平均值来更新模型的参数。尽管 BGD 对参数更新的方向更稳定,但由于计算梯度需要考虑所有样本,因此在大规模数据集上会导致较高的计算开销。
2)SGD(随机梯度下降法):在每次迭代中,随机选择一个样本来计算梯度并更新模型的参数。与 BGD 不同,SGD 每次只使用一个样本,因此计算效率更高。然而,由于单个样本的梯度估计可能存在噪声,SGD 的参数更新方向更加不稳定,收敛速度也相对较慢。
3)MBSGD(小批量随机梯度下降法):MBGD 是 BGD 和 SGD 的折中方法。在每次迭代中,随机选择一个小批量的样本来计算梯度,并根据梯度的平均值来更新模型的参数。这样可以减少计算开销,并且相对于 SGD 而言,参数更新方向更加稳定。
- 对于含有 n个训练样本的数据集,每次参数更新,选择一个大小为 m(m<n) 的mini-batch数据样本计算其梯度,其参数更新公式如下,其中 j 是一个batch的开始:

- 小批量随机梯度下降可以加速收敛,一定程度上有摆脱局部最优的能力(起码比SGD好),但是又可能会存在噪声。
2)动量法:momentum
- 动量(Momentum)是一种优化梯度下降算法的技术,用于加速模型参数的更新,并帮助模型跳出局部最优解。
- 它在训练过程中考虑了之前参数更新的方向和速度。通过将当前梯度与过去梯度加权平均,来获取即将更新的梯度。
- 如图b,可以看出能够加速收敛

- 动量项通常设置为0.9或类似值。
- 参数更新公式如下,其中ρ 是动量衰减率,m是速率(即一阶动量):

3)NAG(Nesterov accelerated gradient)
- 暂时略过,其实它也是加速收敛的方法
4)权重衰减项(weight_decay)
- weight_decay通过对模型的权重进行惩罚来减小权重的大小,用于防止模型过拟合。(简单来说就是控制了模型复杂度,即强制的使权重不会特别大,因为进行了权重衰减,大权重衰减的就多)
- 其实就相当于在梯度后面增加了一个wieght_decay × \times × θ t − 1 \theta_{t-1} θt−1
g t = g t + λ θ t − 1 g_t = g_t + \lambda\theta_{t-1} gt=gt+λθt−1 - 其实就是在梯度中,增加了权重衰减。weight_decay 用于控制模型权重衰减(weight decay)的程度。
- 较小的 weight_decay 值会使权重衰减的影响较小,而较大的值会使权重衰减的影响更显著。
- 这与岭回归类似,岭回归是在损失函数中增加了L2范数的约束,用于防止过拟合(尤其是当特征数大于样本数时,导致多重非线性)
5)总结
- 优点:收敛速度变快,有一定摆脱局部最优的能力
- 缺点:需要手动调参,例如学习率等
1.2、Pytorch实现:torch.optim.SGD
CLASS torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False, maximize=False)
""
params(iterable)- 参数组,优化器要优化的那部分参数。
lr(float)- 初始学习率,可按需随着训练过程不断调整学习率。
momentum(float)- 动量,通常设置为 0.9,0.8
weight_decay(float)- 权重衰减系数,也就是 L2 正则项的系数
nesterov(bool)- bool 选项,是否使用 NAG(Nesterov accelerated gradient)
maximize(bool)- 最大化还是最小化损失函数,默认是最小化,即False
""

1.3、示例
SGD优化器计算过程(以线性回归为例)
建立模型为:y = w^Tx = w1x1+w2x2+w3x3
初始化:y=1*x1+1*x2+1*x3,三个参数w为[1, 1, 1]
损失函数:
l = (pred-gt)**2 = (w1x1+w2x2+w3x3) ** 2
求导(链式法则,先对pred求导,再对w求导):
l'(w1) = 2(pred-gt)*x1
l'(w2) = 2(pred-gt)*x2
l'(w3) = 2(pred-gt)*x3输入数据:
x = tensor([ 1.0943, 1.3479, -1.6927])
预测结果:
p = 1*1.0943+1*1.3479+1*-1.6927=0.74951)当weight_decay = 0
输出梯度:grad: tensor([[ 2.8188, 3.4719, -4.3600]])
手动计算验证:
l'(w1) = 2*(0.7495- -0.5384)*1.0943=2.81869794
l'(w2) = 2*(0.7495- -0.5384)*1.3479=3.47192082
l'(w3) = 2*(0.7495- -0.5384)*-1.6927=-4.36005666权重更新:lr = 0.01
w = tensor([[0.9718, 0.9653, 1.0436]], requires_grad=True)
w1 = 1-0.01*2.81869794=0.9718130206
w2 = 1-0.01*3.47192082=0.9652807918
w3 = 1-0.01*-4.36005666=1.04360056662)当weight_decay = 0.1,lr = 0.01
输出梯度:grad: tensor([[ 2.8188, 3.4719, -4.3600]])l'(w1) = l`(w1) + 0.1*1=2.9188
w1:= 1-0.01*2.9188 = 0.9708
参考链接:https://blog.csdn.net/qq_39707285/article/details/124257377
二、Adagrad:自适应梯度
2.1、算法详解
-
Adagrad优化算法可以自适应调整不同参数的学习率大小,用于解决这样一个问题:常见特征(频繁特征)的参数更新较快,而不常见特征(稀疏特征)的更新较慢
-
Adagrad优化算法是引入了二阶动量,即 v t v_t vt,表示之前所有时间步长(iteration/epoch)的历史梯度的平方和。再将学习率变为 η v t + ε \frac{\eta }{\sqrt{v_t+\varepsilon } } vt+εη,那么学习率就可以自适应更新:如果梯度大(更新较快),学习率就会降低;如果梯度小(更新较慢),学习率就会升高。

-
通过这种自适应调整学习率的方式,每个参数都分别拥有自己的学习率。使得对稀疏特征和频繁特征都能得到较好的更新效果。
-
总结:
优点:Adagrad可以自适应调整学习率,使得对稀疏特征和频繁特征都能得到较好的更新效果。
缺点:仍需要手工设置一个全局学习率;在分母中累积平方梯度,因此在训练过程中累积和不断增长。这会导致学习率不断变小并最终变得无限小,使模型不能继续更新。
2.2、Pytorch的实现:torch.optim.Adagrad
CLASS torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)
''params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认: 1e-2)
lr_decay (float, 可选) – 学习率衰减(默认: 0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
initial_accumulator_value - 累加器的起始值,必须为正。
''

三、RMSprop
3.1、算法详解
- RMSprop是对 Adagrad 的一种改进,将AdaGrad的梯度平方和累加 改为 指数加权的移动平均,参数更新公式:

- RMSprop 通过对梯度平方进行移动平均来计算参数的自适应学习率。具体来说,它引入了一个衰减系数(decay rate,即 ρ \rho ρ,一般设为0.99),用于控制历史梯度平方的权重。
- 可以使学习率的调整更加平稳
3.2、Pytorch的实现:torch.optim.RMSprop
CLASS torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
''params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-2)
momentum (float, 可选) – 动量因子(默认:0)
alpha (float, 可选) – 平滑常数(默认:0.99)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
centered (bool, 可选) – 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化
''

四、Adam
4.1、算法详解
- Adam算法结合了Momentum 和 RMSprop,并进行了偏差修正。
- 也可以从数学理论上解释:Adam 利用梯度的一阶矩估计(momentum)结合过去梯度的更新方向以确定当前梯度的方向,以及二阶矩估计(梯度平方的移动平均)动态的调整学习率。
1)梯度一阶矩估计(通常称为动量):它表示先前梯度的指数加权移动平均,类似于动量优化算法中的动量项。它考虑了过去梯度的方向,并在更新时产生相关影响,有助于加速收敛。
2)梯度二阶矩估计(称为自适应学习率):它表示先前梯度的平方的指数加权移动平均。它衡量了过去梯度大小的变化情况,用于自适应地调整学习率,使得在梯度变化较大时减小学习率,在梯度变化较小时增加学习率。
- Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。


- 总结:
1)自适应学习率:根据梯度的二阶矩估计自动调整学习率大小,在梯度变化较大时减小学习率,在梯度变化较小时增加学习率。这种自适应性使得Adam算法对于不同参数和数据集具有较好的适应性,可以更快地收敛到最优解。
2)动量:利用梯度的一阶矩估计(动量)来考虑过去梯度的方向信息,从而加速模型训练的收敛过程。动量的引入有助于跳出局部最优解。
4.2、Pytorch的实现:torch.optim.Adam
CLASS torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
''
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率(默认:1e-3)
betas (Tuple[float,float], 可选) – 用于计算梯度以及梯度平方的移动平均值的系数(默认:0.9,0.999)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
''

相关文章:

【深度学习中常见的优化器总结】SGD+Adagrad+RMSprop+Adam优化算法总结及代码实现
文章目录 一、SGD,随机梯度下降1.1、算法详解1)MBSGD(Mini-batch Stochastic Gradient Descent)2)动量法:momentum3)NAG(Nesterov accelerated gradient)4)权重衰减项(we…...

山东大学软件学院考试回忆——大二上
文章目录 学习科目整体回忆上课考试回忆Web技术大学物理概率与统计计算机组织与结构离散数学(2)数据结构(双语) 学习科目 Web技术大学物理概率与统计计算机组织与结构离散数学(2)(双语…...

【Express.js】异常分类和日志分级
异常分类和日志分级 第一章已经介绍过全局的异常处理了,但之前的做法过于简单,一股脑的捕获并返回。这一节我们将对异常进行细致的分类,并且日志也做标准化的分级。 准备工作 一个基础的 evp-express 项目 NodeJS Error 先了解一下 Node…...
k8s webhook实例,java springboot程序实现 对Pod创建请求添加边车容器 ,模拟istio实现日志文件清理
k8s webhook实例,java springboot程序实现 对Pod创建请求添加边车容器 ,模拟istio实现日志文件清理 大纲 背景与原理实现流程开发部署my-docker-demo-sp-user服务模拟业务项目开发部署my-sidecar服务模拟边车程序开发部署服务my-docker-demo-k8s-opera…...

关于electron的问题汇总
1. electron-builder打包慢出错的问题 由于网络原因,在进行builder打包时,可能会等很长时间,直到最后还是以失败告终。 如果是第一次进行builder打包,会去下载winCodeSign、nsis、nsis-resources,往往都是第一个就卡住…...
ps 给衣服换色
可以通过色相饱和度来改变颜色 但如果要加强对比 可以通过色阶或曲线来调整 针对整体 调整图层-色相/饱和度 着色 给整个画面上色 选区-遮罩-取出来 然后调整图层-色相/饱和度也可以 或者以有图层-色相饱和度后 选区 按ctrli使其遮罩 同时按alt鼠标左键单机 ctrli反相…...

AI人工智能未来在哪里?2023年新兴产业人工智能有哪些就业前景?
AI人工智能未来在哪里?2023年新兴产业人工智能有哪些就业前景? 随着科技的不断发展,人工智能技术也在不断地进步。在数字化时代,人工智能技术已经渗透到了我们生活的各个方面。2023年为止中国产业80%已经实现半自动化,…...
组件间通信案例练习
1.实现父传子 App.vue <template><div class"app"><tab-control :titles["衣服","鞋子","裤子"]></tab-control><tab-control :titles["流行","最新","优选","数码&q…...

【matlab】机器人工具箱快速上手-正运动学仿真(代码直接复制可用)
安装好机器人工具箱,代码复制可用,按需修改参数 1.建模 %%%%%%%%SCARA机器人仿真模型 l[0.457 0.325]; L(1) Link(d,0,a,l(1),alpha,0,standard,qlim,[-130 130]*pi/180);%连杆1 L(2)Link(d,0,a,l(2),alpha,pi,standard,qlim,[-145 145]*pi/180);%连杆…...
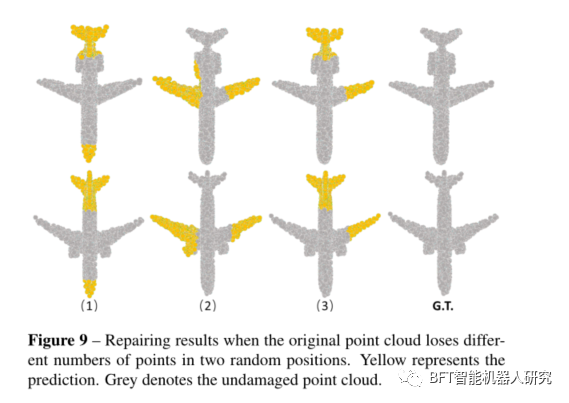
论文解读|PF-Net:用于 3D 点云补全的点分形网络
原创 | 文 BFT机器人 01 背景 从激光雷达等设备中获取的点云往往有所缺失(反光、遮挡等),这给点云的后续处理带来了一定的困难,也凸显出点云补全作为点云预处理方法的重要性。 点云补全(Point Cloud Completion&#x…...
网络安全(零基础)自学
一、网络安全基础知识 1.计算机基础知识 了解了计算机的硬件、软件、操作系统和网络结构等基础知识,可以帮助您更好地理解网络安全的概念和技术。 2.网络基础知识 了解了网络的结构、协议、服务和安全问题,可以帮助您更好地解决网络安全的原理和技术…...

Spring Security 身份验证的基本类/架构
目录 1、SecurityContextHolder 核心类 2、SecurityContext 接口 3、Authentication 用户认证信息接口 4、GrantedAuthority 拥有权限接口 5、AuthenticationManager 身份认证管理器接口 6、ProviderManager 身份认证管理器的实现 7、AuthenticationProvider 特定类型的…...
市值超300亿美金,SaaS独角兽Veeva如何讲好中国故事?
“全球前50的药企,有47家正在使用Veeva。” 提到Veeva Systems(以下简称“Veeva”),可能很多人并不熟悉。但是生命科学业内人士都知道,Veeva是全球头部的行业SaaS服务商。以“为生命科学行业构建行业云”为使命&#x…...

编译内联导致内存泄漏的问题定位修复
作者:0x264 问题 线上长时间存在一个跟异步 inflate 相关的量级较大的内存泄漏,如下所示: 第一次分析 从内存泄漏粗略看有几个信息: 被泄漏的Activity有很多,所以可能跟某个具体业务的关系不大引用链特别短…...

基于WebSocket实现的后台服务
基于WebSocket实现的后台服务,用于接收客户端的心跳消息,并根据心跳消息来维护客户端连接。 具体实现中,服务启动后会创建一个HttpListener对象,用于监听客户端的WebSocket连接请求。当客户端连接成功后,服务会为每个…...
Go语言中的结构体详解
关于 Golang 结构体 Golang 中没有“类”的概念,Golang 中的结构体和其他语言中的类有点相似。和其他面向对 象语言中的类相比,Golang 中的结构体具有更高的扩展性和灵活性。 Golang 中的基础数据类型可以表示一些事物的基本属性,但是当我们…...
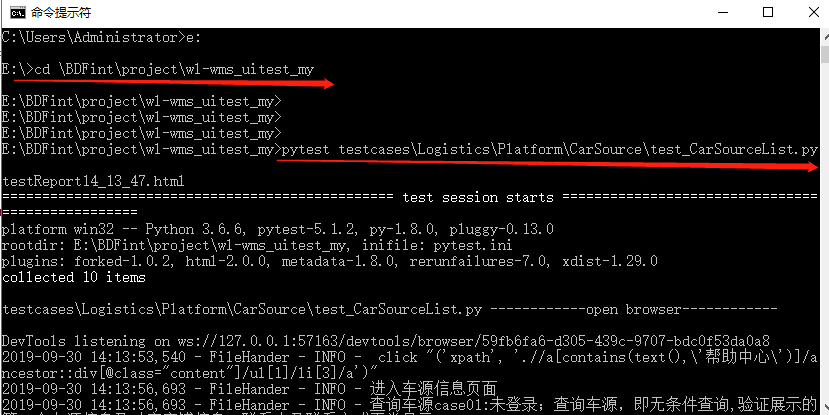
pytest自动化测试指定执行测试用例
1、在控制台执行 打开cmd,进入项目目录 指定执行某个模块 pytest testcases\Logistics\Platform\CarSource\test_CarSourceList.py 指定执行某个目录及其子目录的所有测试文件 pytest testcases\Logistics\Platform\CarSource 指定执行某个模块的某个类的某个测试用例 pyte…...

英伟达 H100 vs. 苹果M2,大模型训练,哪款性价比更高?
M1芯片 | Uitra | AMD | A100 M2芯片 | ARM | A800 | H100 关键词:M2芯片;Ultra;M1芯片;UltraFusion;ULTRAMAN;RTX4090、A800;A100;H100;LLAMA、LM、AIGC、CHATGLM、LLVM、LLM、LLM…...

var、let和const的区别
先简单了解一下 var声明的变量会挂载在window上,而let和const声明的变量不会: var a 100; console.log(a,window.a); // 100 100let b 10; console.log(b,window.b); // 10 undefinedconst c 1; console.log(c,window.c); // 1 undefined v…...

(css)AI智能问答页面布局
(css)AI智能问答页面布局 效果: html <!-- AI框 --><div class"chat-top"><div class"chat-main" ref"chatList"><div v-if"!chatList.length" class"no-message"><span>欢迎使…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
