GoogleLeNet V2 V3 —— Batch Normalization
文章目录
- Batch Normalization
- internal covariate shift
- 激活层的作用
- BN执行的位置
- 数据白化
- 网络中的BN层
- 训练过程
- BN的实验效果
- MNIST
- 与GoogleLeNet V1比较
GoogleLeNet出来之后,Google在这个基础上又演进了几个版本,一般来说是说有4个版本,之前的那个是V1,然后有一个V2,V3和V4。
其实我个人感觉V2和V3应该是在一起的,都是综合了两篇论文中的一些改进点来的:
- Accelerating deep network training by reducing internal covariate shift
- Rethinking the Inception Architecture for Computer Vision
其中,第一篇是提出了一个重要的概念:Batch Normalization,是针对内部协变量偏移问题的,简单的说就是加速训练过程。把BN作为激活层之前的另外一个网络层,可以加速网络训练的收敛速度。
第二篇就提出了一些新的卷积方法等,然后总和第一篇论文一起就提出了一个inception v2的网络结构,没有明确提到v3,但是其中的一些变形作为了v3版本。
我们就来看一下这两篇论文说了点啥,这个v2和v3又改进了点啥。
Batch Normalization
internal covariate shift
讲BN之前,肯定要说说BN到底是解决一个什么问题,在论文中提到的就是internal covariate shift问题,翻译过来是内部协变量偏移。不明觉厉,这个看不太懂是什么东西。
原文中的描述为:
Training Deep Neural Networks is complicated by the fact that the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change.
This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities. We refer to this phenomenon as internal covariate shift, and address the problem by normalizing layer inputs。
大致意思是在训练的反向传播过程中,每个输入数据的分布情况回发生变化,在计算损失的之后,这一层的输出也会发生变化,从而导致下一层的输入数据分布发生变化。这种情况就叫做内部协变量偏移。
简单点说就是网络的隐藏层数据分布变化很大,容易出现梯度消失和梯度爆炸,导致训练过程很难收敛。一个梯度一下大到天上,一下就等于0,确实很难收敛。
那么BN的基本逻辑就是针对每个训练的batch数据,在每个激活层(Sigmond或者ReLU之类)前增加一个BN层,也就是做一次数据标准化,把上一层的输出线性变化到一个固定的分布内(fixed distribution)
激活层的作用
这里增加一点,就是之前一直没太弄明白激活层的作用。看完这篇论文之后大概了解了。整个网络,中间基本都是卷积和全连接层,不管是卷积还是全连接层,都是针对前一层数据的一种线性变换。也就是前一层数据的一种多项式变化,如果中间没有激活层的话,那么实际上无论增加多少层,都可以简化成一层,因为线性变化是可以叠加的。
举个例子,如果第一层的处理是:
F ( x ) = 2 x + 3 F(x)=2x+3 F(x)=2x+3
第二层的处理是:
H ( x ) = 4 x − 4 H(x)=4x-4 H(x)=4x−4
这里的x就是上一层的 F ( x ) F(x) F(x),所以就是
H ( x ) = 4 ( 2 x + 3 ) − 4 = 8 x − 8 H(x)=4(2x+3)-4=8x-8 H(x)=4(2x+3)−4=8x−8
那么就可以简化成一层。复杂的线性变化也是一样的。但是如果增加了激活层的话,就不一样了,激活层是非线形函数,不满足
f ( x + y ) = f ( x ) + f ( y ) f(x+y)=f(x) + f(y) f(x+y)=f(x)+f(y),所以就不存在上述的变换。
这样就可以增强模型的表达能力(reprensetation power),就是对数据分布的拟合能力。
所以基本上,在网络结构里,每个卷积层后面都会跟一个非线性层(池化或者激活)。
BN执行的位置
论文中的描述是:To Batch-Normalize a network, we specify a subset of activations and insert the BN transform for each of them。
增加在所有的激活层之前。
数据白化
论文中提到:By fixing the distribution of the layer inputs x as the training progresses, we expect to improve the training speed. It has been long known that the network training converges faster if its inputs are whitened, linearly transformed to have zero
means and unit variances, and decorrelated。
这里提到就是利用了LeCun 1998年的论文中提到的,白化(whiten)的输入数据可以加速训练。而这个白化数据就是指数据分布符合均值为0,方差为1。
白化过程为:一个d维的矢量样本( x = ( x ( 1 ) , x ( 2 ) . . . . x ( d ) ) x=(x^{(1)},x^{(2)}....x^{(d)}) x=(x(1),x(2)....x(d)))的白化过程:
x ^ ( k ) = x ( k ) − E [ x ( k ) ] V a r [ x ( k ) ] \hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}} x^(k)=Var[x(k)]x(k)−E[x(k)]
把每一维计算完成之后就形成了服从0-1分布的 x ^ \hat{x} x^向量。
网络中的BN层
在白化之后,实际上还需要做一个线性变换:
y ( k ) = γ ( k ) x ^ ( k ) + β ( k ) y^{(k)}=\gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)} y(k)=γ(k)x^(k)+β(k)
至于为什么要增加这么一个动作,论文中是说:
Note that simply normalizing each input of a layer may change what the layer can represent. For instance, normalizing the inputs of a sigmoid would constrain them to the linear regime of the nonlinearity.
我理解是直接标准化会降低网络的表达能力,可能是直接强行拉到一个0-1的分布,会造成一些损失吧。所以可以做一些拉伸和偏移(正态分布的那个图做一些拉伸和偏移),然后在学习的过程中去动态的调整这两个参数 γ \gamma γ和 β \beta β。也就是学习到底是拉伸多少,偏移多少能更好的拟合数据。
上面的数据白话相当于是把一个样本作了标准化,然后需要把一个训练batch的数据一起做标准化。
论文中是说:since we use mini-batches in stochastic gradient training, of the mean and variance each mini-batch produces estimates of each activation。
也就是说为每个批次也要做一个normalization。
计算方法为:

从上图可以看出来,前面三步就是对数据作了一次白化(类似),只是方向上需要理解一下。
比如输入为一张图像,图像为 p ∗ q p * q p∗q宽,总共有m张图像,那么这里的向量 x x x的长度就是 m m m,也就是沿着图像数的方向。总共有p✖️q个这样的向量。也就是要做p✖️q次normalization计算。
这样就完成了BN层的计算。计算之后相当于这个批次中的图像中的每个像素都是服从同一分布的,但是 γ \gamma γ和 β \beta β不同。
训练过程
以SGD,随机梯度下降的反向传播算法来说:
从输出层开始,计算完loss和随机梯度后,就会向后传播,那么这个BN层也是需要传播的。
通过下图,就可以计算出 γ \gamma γ和 β \beta β每次的更新量 Δ γ \Delta \gamma Δγ和 Δ β \Delta \beta Δβ

整个训练过程为:

针对每一个BN层,通过上述的计算过程进行训练。
BN的实验效果
MNIST
在手写上与最古老的LeNet比较,达到同样的精确度,训练次数大大减少。
与GoogleLeNet V1比较
针对V1做了一些改动
- 增大学习率
- 去掉DropOut
- 去掉LRN
- 重新打乱训练集
- 减少图像的扩展
做了下面几个模型的比对
- 基于上面改动,增加了BN层的基本模型:BN-Baseline
- Baseline的基础上,学习率提升5倍到 0.0075:BN-x5
- 学习率提升30倍到0.045:BN-x30
- 激活层使用Sigmond,5倍学习率的BN-x5-Sigmond
结论是在BN-x5的情况下,达到v1版本的精确率,训练次数最少。
而BN-30可以达到更高的精度,但是训练次数要多一点。
Sigmond根本达不到这个精度,BN更适用于ReLU激活层。
相关文章:

GoogleLeNet V2 V3 —— Batch Normalization
文章目录 Batch Normalizationinternal covariate shift激活层的作用BN执行的位置数据白化网络中的BN层训练过程 BN的实验效果MNIST与GoogleLeNet V1比较 GoogleLeNet出来之后,Google在这个基础上又演进了几个版本,一般来说是说有4个版本,之前…...
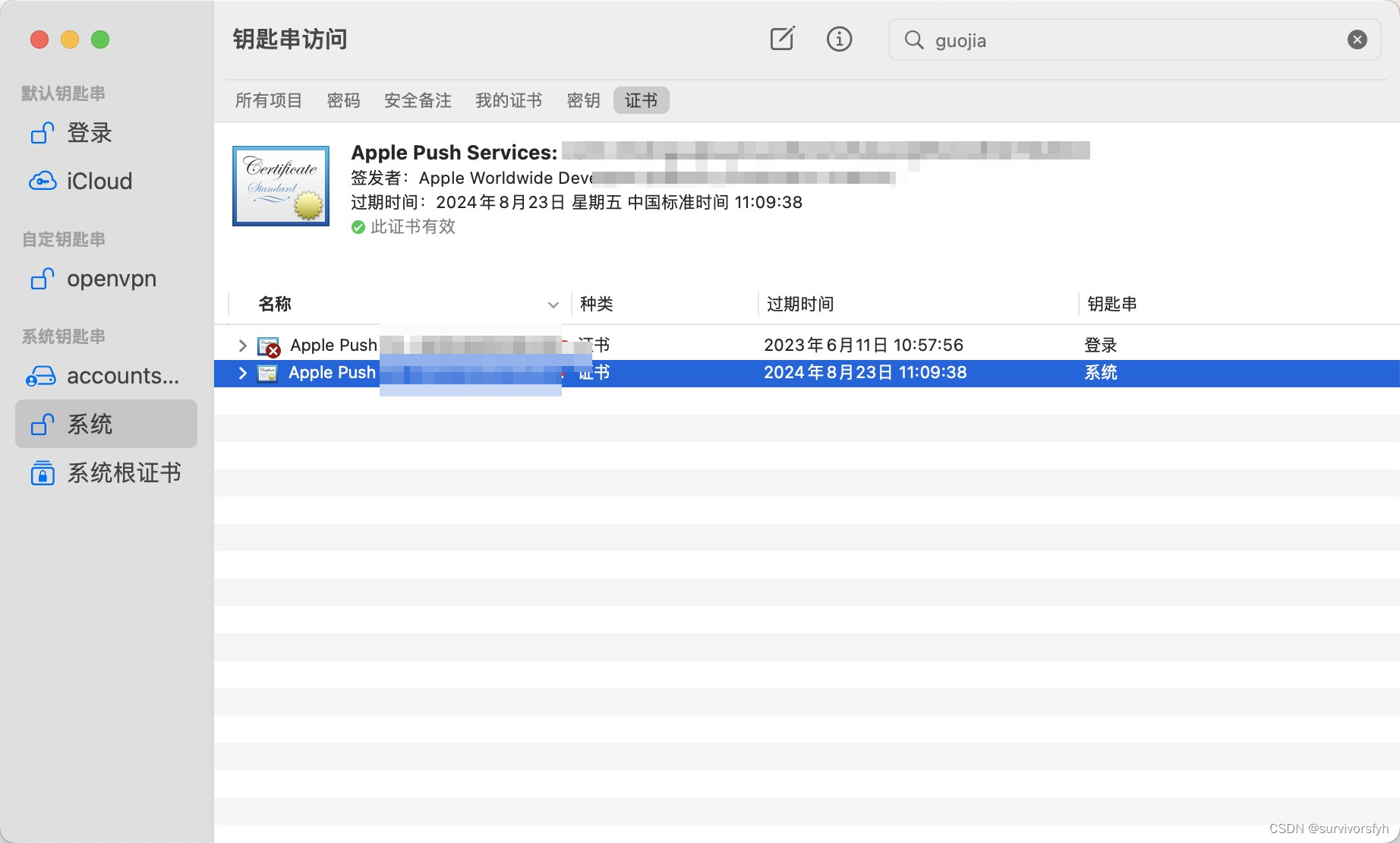
Mac 系统钥匙串证书不受信任
Mac 系统钥匙串证书不受信任 解决办法 通过尝试安装 Apple PKI 的 Worldwide Developer Relations - G4 (Expiring 12/10/2030 00:00:00 UTC) 解决该异常问题 以上便是此次分享的全部内容,希望能对大家有所帮助!...
一个企业级的文件上传组件应该是什么样的
目录 1.最简单的文件上传 2.拖拽粘贴样式优化 3.断点续传秒传进度条 文件切片 计算hash 断点续传秒传(前端) 断点续传秒传(后端) 进度条 4.抽样hash和webWorker 抽样hash(md5) webWorker 时间切片 5.文件类型判断 通过文件头判断文件类型 6.异步并发数控制(重要…...

安全渗透重点内容
this是js中的一个关键字,在不同的场合使用,this的值会发生变化,下面我将详细的介绍this在函数中的各种指向。 在方法中,this表示该方法所属的对象。 如果单独使用,this表示全局对象。 在函数中,this表示全…...
【触觉智能Purple Pi OH开发板体验】开箱体验:开源主板Purple Pi RK3566 上手指北
前言 前段时间收到来自【电子发烧友】的一款开发板,名叫:PurplePi,216G售价仅249元。它使用的芯片是rk3566,适配的OpenHarmony版本为3.2 Release 是目前最便宜的OpenHarmony标准系统开源开发板,并且软硬件全部开源&am…...

flink1.16使用消费/生产kafka之DataStream
flink高级版本后,消费kafka数据一种是Datastream 一种之tableApi。 上官网 Kafka | Apache Flink Kafka Source 引入依赖 flink和kafka的连接器,里面内置了kafka-client <dependency><groupId>org.apache.flink</groupId><arti…...

【多任务编程-线程通信】
进程/线程通信的方式 某些应用程序中,进程/进程和线程/线程之间不可避免的进行通信,进行消息传递,数据共享等 同一进程的线程之间通信方式包括Windows中常用Event, Message等。 不同进程之间的通信可以利用Event, FileMapping(内存共享), W…...

K8S暴露pod内多个端口
K8S暴露pod内多个端口 一、背景 公司统一用的某个底包跑jar服务,只暴露了8080端口 二、需求 由于有些服务在启动jar服务后,会启动多个端口,除了8080端口,还有别的端口需要暴露,我这里就还需要暴露9999端口。 注&a…...
Python 列表
""" #list函数 ls list() #创建一个空列表 print(list()) print(list(str(1234)))#[1, 2, 3, 4] print(list(range(5)))#[0, 1, 2, 3, 4] print(list((1,2,3,4)))#[1, 2, 3, 4] print(list(Lift is short, you need python))#注意空格也算一个字符 #[L, i, f,…...
Rabbitmq的安装与使用(Linux版)
目录 Rabbitmq安装 1.在Ubuntu上安装RabbitMQ: 打开终端,运行以下命令以更新软件包列表: 安装RabbitMQ: 安装完成后,RabbitMQ服务会自动启动。你可以使用以下命令来检查RabbitMQ服务状态: 2.在CentOS…...
Kubernetes对象深入学习之四:对象属性编码实战
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《Kubernetes对象深入学习》系列的第四篇,前面咱们读源码和文档,从理论上学习了kubernetes的对象相关的知识ÿ…...

深度学习入门教程(2):使用预训练模型来文字生成图片TextToImageGenerationWithNetwork
本深度学习入门教程是在polyu HPCStudio 启发以及资源支持下进行的,在此也感谢polyu以及提供支持的老师。 本文内容:在GoogleColab平台上使用预训练模型来文字生成图片Text To Image Generation With Network (1)你会学到什么&a…...
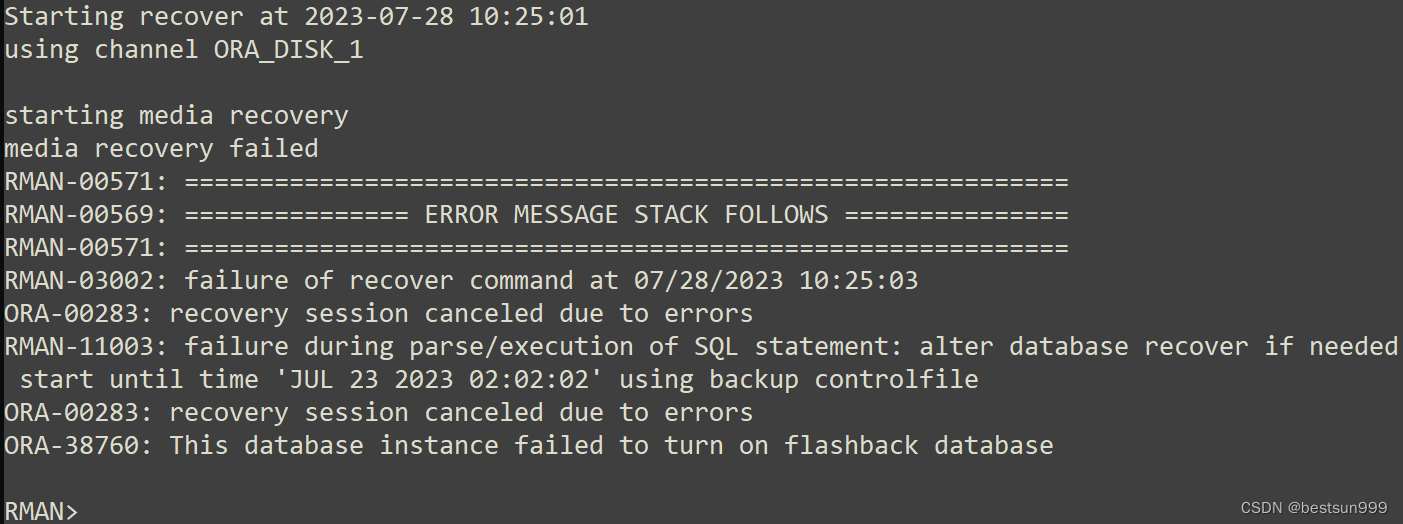
ORA-38760: This database instance failed to turn on flashback database
早晨接一个任务,使用rman备份在虚拟化单机上恢复实例,恢复参数文件、控制文件和数据文件都正常,recover归档时报错如下: Starting recover at 2023-07-28 10:25:01 using channel ORA_DISK_1 starting media recovery media reco…...

避免低级错误:深入解析Java的ConcurrentModificationException异常
在软件开发中,我们常常会遇到各种错误和异常。其中有一类比较低级但又常见的错误就是ConcurrentModificationException异常。最近了我就写了个这种异常,这个异常通常发生在使用迭代器遍历集合时,同时对集合进行修改,从而导致迭代器…...
7.28
1.思维导图 2.qt的sever #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include<QTcpServer> //服务器类 #include<QTcpSocket> //客户端类 #include<QMessageBox> //对话框类 #include<QList> …...
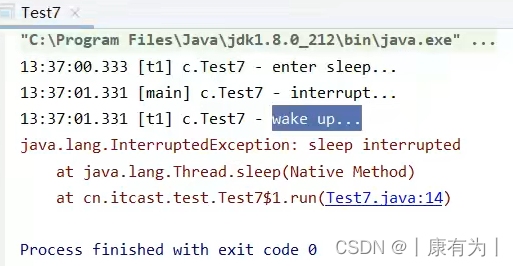
java线程中的常见方法(详解)
方法简介 方法名 功能 说明 start() 启动一个新线程,在新的线程运行 run 方法中的代码 start 方法只是让线程进入就绪,里面代码不一定立刻运行(CPU 的时间片还没分给它)。每个线程对象的start方法只能调用一次,如…...

线程池参数配置
上次面试被人问到,如果是IO 密集型的任务,该如何配置合适的线程数,当初我说要按照IO具体的请求毫秒时间,来配置具体的线程数。 NthreadsNcpu*(1w/c) 公式中 W/C 为系统 阻塞率 w:等待时间 c:计算时间一般情况下,如果存…...

Spread for Winform 16.2.20231.0 (SP2) Crack
Spread for Winform 16.2.20231.0 (SP2)发布。此版本包含针对客户报告的问题的重要修复: 安装版本 16 后,FarPoint.Localization.dll 将丢失。 将数据绑定到 Spread 时会出现 InvalidOperationException。 通过 Spread Designer 设置的上标将不会保留。…...

Go程序结构
Go程序结构 1、名称 名称的开头是一个字母或下划线,且区分大小写。 实体第一个字母的大小写决定其可见性是否跨包: 若名称以大写字母开头,它是导出的,对包外是可见和可访问的,可以被自己包以外的其他程序所引用…...

JAVA面试总结-Redis篇章(四)——双写一致性
JAVA面试总结-Redis篇章(四)——双写一致性 问:redis 做为缓存,mysql的数据如何与redis进行同步呢?第一种情况,如果你的项目一致性要求高的话 采用以下逻辑我们应该先删除缓存,再修改数据库&…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
