第四章 No.1树状数组的原理与使用
文章目录
- 应用问题
- 原理
- 树状数组练习题
- 241. 楼兰图腾
- 242. 一个简单的整数问题
- 243. 一个简单的整数问题2
- 244. 谜一样的牛
线段树的反面:树状数组原理复杂,实现简单
应用问题
支持两个操作:快速求前缀和任意地修改某个数,时间复杂度为 O ( l o g n ) O(logn) O(logn)
用前缀和数组,求前缀和的复杂度为 O ( 1 ) O(1) O(1),但是任意修改某个数的复杂度为 O ( n ) O(n) O(n)
用数组,求前缀和的复杂度为 O ( n ) O(n) O(n),修改某个数的时间复杂度为 O ( 1 ) O(1) O(1)
而使用树状数组,可以以适中的时间复杂度解决以上问题
原理
原理就是二进制表示,一个整数x,将其二进制表示后,可以直观地发现该数可以表示成多个2的幂相加
比如10110可以表示成: 2 1 + 2 2 + 2 4 2^1+2^2+2^4 21+22+24
在最坏情况下,一个32位整数n需要将32个2的幂相加,即 O ( l o g n ) O(logn) O(logn)
分析一下:将1~x整个区间划分后,每个子区间是怎样的?
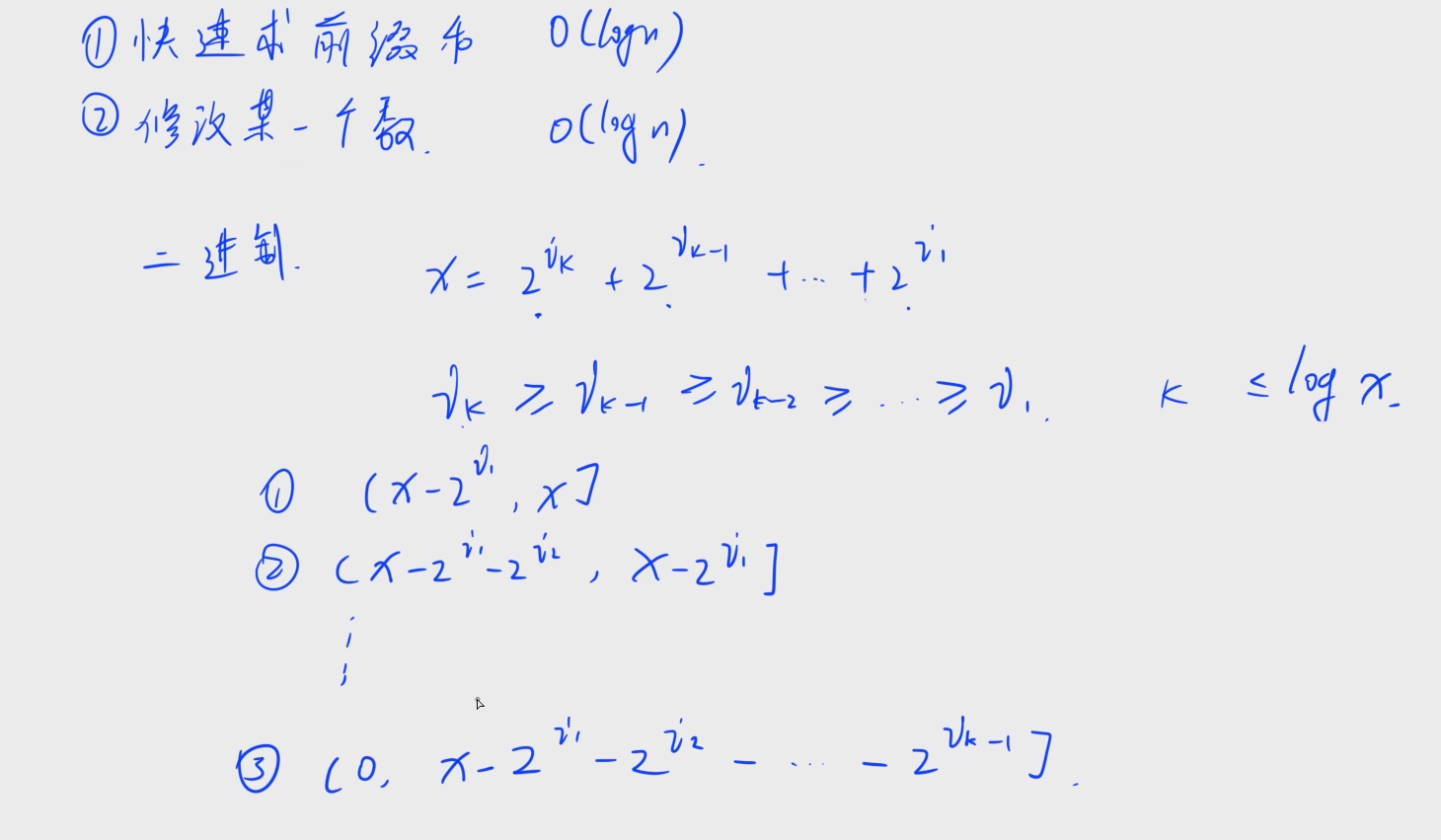
每一个区间长度都为2的幂
第一个区间为 ( x − 2 i 1 , x ] (x-2^{i_1}, x] (x−2i1,x],长度为 2 i 1 2^{i_1} 2i1
第二个区间为 ( x − 2 i 1 − 2 i 2 , x − 2 i 1 ] (x-2^{i_1}-2^{i_2}, x-2^{i_1}] (x−2i1−2i2,x−2i1],长度为 2 i 2 2^{i_2} 2i2
…
最后一个区间为 ( 0 , x − 2 i 1 − 2 i 2 − . . . − 2 i k − 1 ] (0, x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}] (0,x−2i1−2i2−...−2ik−1],长度为 2 i k 2^{i_k} 2ik
其中k为x中1的个数
可以发现,区间 ( l , r ] (l, r] (l,r]可以表示成 [ r − l o w b i t ( r ) + 1 , r ] [r-lowbit(r)+1, r] [r−lowbit(r)+1,r]
因为区间长度一定是r的最后一位1对应的幂,即lowbit(r)
假设数组长度为n,对于1~n之间的所有数,将其作为区间 [ r − l o w b i t ( r ) + 1 , r ] [r-lowbit(r)+1, r] [r−lowbit(r)+1,r]的右端点,则这些区间将有重复地覆盖1~n整个区间
长度为16的数组的划分:
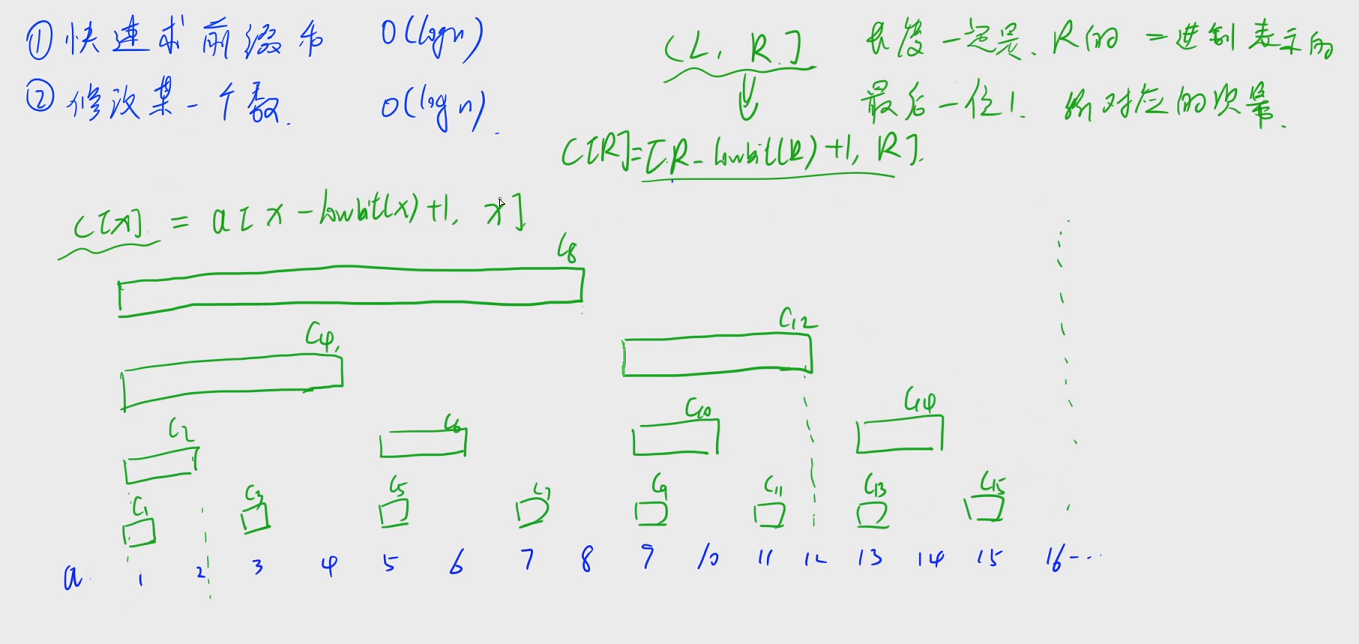
思考每个区间之间的关系,当前区间可以由哪些区间得到?则有:
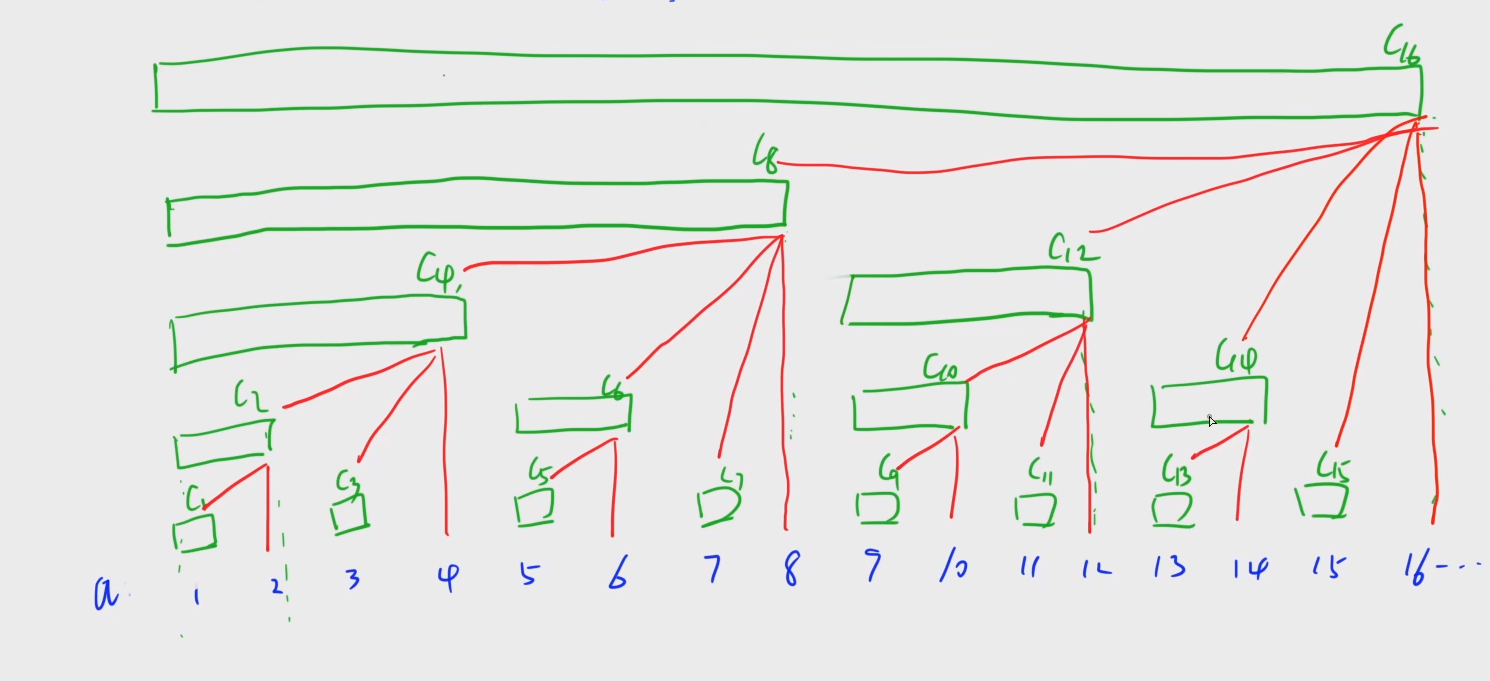
将每段区间看成节点,再看上面这张图
连接了存在关系的区间,那么所有区间就构成了一颗树。这便是树状数组名字的由来,十分的形象,思考父子节点之间的关系
对于 C 16 C_{16} C16这个区间,它由 ( a 16 , C 15 , C 14 , C 12 , C 8 ) (a_{16}, C_{15}, C_{14}, C_{12}, C_{8}) (a16,C15,C14,C12,C8)组成,再举例几个区间后
可以看出规律:区间 C n C_n Cn由区间 ( a n , C . . . ) (a_n, C...) (an,C...)组成,其中除了 a n a_n an,剩下区间的下标k加上lowbit(k)后的结果为16
15:01111 + 1 = 10000,01111 - 1 = 01110
14:01110 + 10 = 10000,01110 - 10 = 01100
12:01100 + 100 = 10000,01100 - 100 = 01000
8:01000 + 1000 = 10000,01000 - 1000 = 00000
观察这些下标k的规律,每次下标变小都是减去了lowbit(k),当下标为0,说明当前节点没有子节点了
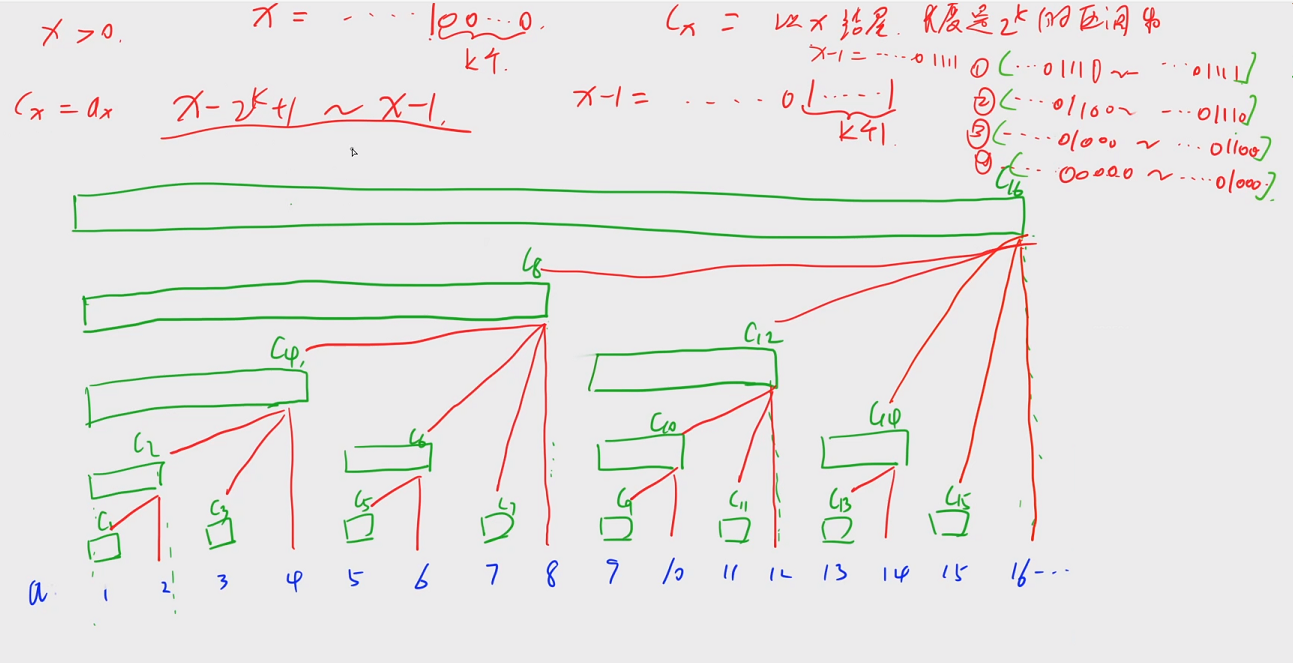
通过以上推导,可以发现子节点下标到父节点下标的规律:
假设当前区间为 C x C_x Cx,那么 C x + l o w b i t ( x ) C_{x+lowbit(x)} Cx+lowbit(x)是其父节点, C x + l o w b i t ( l o w b i t ( x ) ) C_{x+lowbit(lowbit(x))} Cx+lowbit(lowbit(x))是其祖父节点…直到下标超过n。此时作为 C x C_x Cx的祖先节点不存在
为什么要知道子节点到父节点的关系?由于 C x C_x Cx维护着数组中的某段区间和,并且这些区间之间存在着重叠,修改数组中的任意一个数后,必定会向上影响其的父节点的区间和,此时只能通过子节点不断地更新到根节点,才能维护正确的数据。所以知道子节点到父节点的关系是有必要的
总结一下:
子节点到父节点的推导:假设子节点在数组中的下标为x,需要不断地对子节点的下标加上lowbit(x),获取其父节点的下标直到下标超过数组长度的最大值
由此就能实现修改任意位置的成员
// 对原数组x下标位置上的数+c
void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
其中tr数组是维护的树状数组
第二个问题:如何获取前缀和?

还是这张图,假设要获取前16个数的和,直接返回树状数组的 C 16 C_{16} C16即可,也就是树状数组的第16个成员
假设要获取前14个数的和,需要返回 C 14 + C 12 + C 8 C_{14}+C_{12}+C_8 C14+C12+C8,将它们的下标转换成二进制
001110
001100
001000
000000
可以发现,在整个数为0之前,二进制表示的最后一个1不断被减去
经过归纳,求前i个数的和时,需要对树状数组中的数进行累加,这些数的下标从i开始,不断地减去最后一位1,直到i为0
注意不要先减去1再不断减去lowbit(k),那是求节点的子节点方式
直接减去lowbit(k)是求前缀和的方式
int sum(int x)
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}
如何建立数组数组?
建立树状数组的方式有两种,最简单的方式是直接调用add将需要修改的数添加(一开始树状数组的所有成员为0),时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
此外,还能直接根据定义建数组,先求出原数组a[n]的前缀和数组s[n]
树状数组中,区间 ( r − l o w b i t ( r ) + 1 , r ) (r-lowbit(r)+1, r) (r−lowbit(r)+1,r)的值为s[r] - s[r - lowbit[r]],此时直接修改原数组即可
由于不用调用add,所以时间复杂度为 O ( n ) O(n) O(n),但该做法额外维护了一个前缀和数组
树状数组练习题
241. 楼兰图腾
241. 楼兰图腾 - AcWing题库
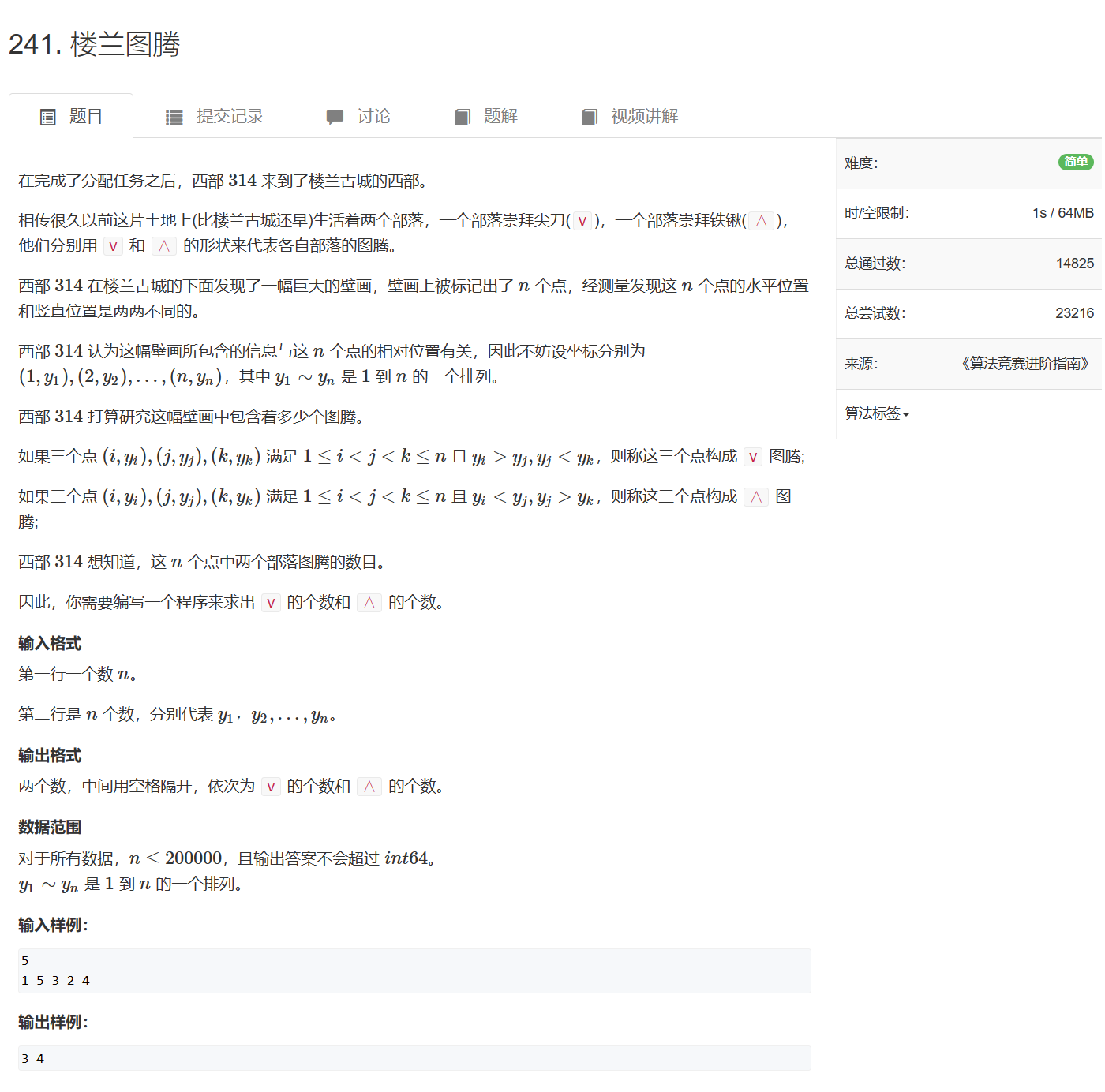
划分所有的纵坐标成k个集合,每个集合表示纵坐标为 y k y_k yk时,能构成的v和∧的数量
( x , y k ) (x, y_k) (x,yk)能构成的v的数量:在横坐标小于x的坐标中,纵坐标大于 y k y_k yk的坐标数量乘以横坐标大于x的坐标中,纵坐标大于 y k y_k yk的坐标数量
( x , y k ) (x, y_k) (x,yk)能构成的∧的数量:在横坐标小于x的坐标中,纵坐标小于 y k y_k yk的坐标数量乘以横坐标大于x的坐标中,纵坐标小于 y k y_k yk的坐标数量
树状数组存储纵坐标小于等于当前下标的坐标数量,比如tr[i]表示纵坐标小于等于i的坐标数量
将所有纵坐标按照横坐标的升序顺序存储到数组a中,遍历a[i]时,需要求出纵坐标小于a[i]以及纵坐标大于a[i]的坐标数量,分别用l数组和g数组存储。这是横坐标小于x且纵坐标大于或小于a[i]的坐标数量,也就是前缀和
a[i]的前缀和求完后,需要将tr[a[i]]加1,表示纵坐标小于等于a[i]的坐标数量+1
前缀和求完后再求后缀和,便能得到答案
tr[i]存储纵坐标小于等于a[i]的坐标数量,如何求纵坐标小于a[i]的坐标数量?tr[a[i]-1]即可
如何求纵坐标大于a[i]的坐标数量,tr[max] - tr[a[i]]即可,max表示所有纵坐标中的最大值
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 2e5 + 10;
int a[N], l[N], g[N], tr[N];
int n;int lowbit(int x)
{return x & (~x + 1);
}int sum(int x)
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]);for (int i = 1; i <= n; ++ i ){int y = a[i];g[i] = sum(n) - sum(y);l[i] = sum(y - 1);add(y, 1);}LL res1 = 0, res2 = 0;memset(tr, 0, sizeof(tr));for (int i = n; i >= 1; -- i ){int y = a[i];res1 += g[i] * (LL)(sum(n) - sum(y));res2 += l[i] * (LL)sum(y - 1);add(y, 1);}printf("%lld %lld\n", res1, res2);return 0;
}
242. 一个简单的整数问题
242. 一个简单的整数问题 - AcWing题库
将某段区间中的数加上c,而不是修改成c,使用差分数组可以完美解决此问题
查询原数组中某个数的值,使用差分数组需用 O ( n ) O(n) O(n),总的复杂度为 O ( n m ) O(nm) O(nm),可能会超时,所以考虑如何优化
通过差分数组求原数组的某个数其实是一个前缀和操作,要优化 O ( n ) O(n) O(n)的前缀和可以考虑树状数组。自然地,树状数组存储的是原数组的差分信息,1. 将区间 [ l , r ] [l, r] [l,r]加上c时,只用修改 l l l和 r + 1 r+1 r+1位置上的数即可,复杂度为 O ( l o g n ) O(logn) O(logn) 2. 求原数组的某个数时,使用树状数组的sum操作即可,时间复杂度为 O ( l o g n ) O(logn) O(logn)
总的时间复杂度为 O ( m l o g n ) O(mlogn) O(mlogn),不会超时
#include <iostream>
using namespace std;typedef long long LL;
const int N = 1e5 + 10;
int a[N], tr[N];
int n, m;int lowbit(int x)
{return x & (~x + 1);
}void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}LL sum(int x)
{LL res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]);for (int i = 1; i <= n; ++ i ) tr[i] = a[i] - a[i - lowbit(i)];int l, r, d, x; char op[2];while (m -- ){scanf("%s", op);if (op[0] == 'C') {scanf("%d%d%d", &l, &r, &d);add(l, d); add(r + 1, -d);}else{scanf("%d", &x);printf("%lld\n", sum(x));}}return 0;
}
debug:add(l, d); add(r + 1, -d),后面那个add习惯地写成了add(r + 1, d)
以及可能存在的爆int问题,一直都没有特别注意
243. 一个简单的整数问题2
243. 一个简单的整数问题2 - AcWing题库
需要实现两个操作:1. 对区间中的所有数加上一个数 2. 求区间和
与上题思路类似,保存差分信息以实现第一个操作
求区间和时,思考如何求原数组中的某个数 a i a_i ai?这需要对差分数组前缀求和
那么如何求原数组中的区间和呢?分别求出区间中的每个数吗?就算对前缀和求解过程进行优化,也要 O ( n ) O(n) O(n)
思考如何优化对n个数求前缀和?如下图,列出 a [ 1 ] a[1] a[1]到 a [ x ] a[x] a[x]中的每个数需要的差分信息,补全这些差分信息(图中红蓝部分)

可以发现区间 ( 1 , x ) (1, x) (1,x)的和就是蓝色部分,等于所有的和减去红色的和
( b 1 + b 2 + . . . + b x ) ( x + 1 ) − ( 1 b 1 + 2 b 2 + . . . + x b x ) (b_1+b_2+...+b_x)(x+1)-(1b_1+2b_2+...+xb_x) (b1+b2+...+bx)(x+1)−(1b1+2b2+...+xbx)
就是 b i b_i bi的前缀和乘以 ( x + 1 ) (x+1) (x+1)再减去 i b i ib_i ibi的前缀和
b i b_i bi的前缀和可以通过树状数组tr1维护, i b i ib_i ibi的前缀和可以通过树状数组tr2维护
对于题目需要的两个操作,维护这两个数组可以实现第二个操作,同时tr1数组能实现第一个操作
#include <iostream>
using namespace std;typedef long long LL;
const int N = 1e5 + 10;LL tr1[N], tr2[N];
int a[N];
int n, m;int lowbit(int x)
{return x & (~x + 1);
}void add(LL tr[], int x, LL c)
{for (int i = x; i <= n; i += lowbit(i) ) tr[i] += c;
}LL sum(LL tr[], int x)
{LL res = 0;for (int i = x; i; i-= lowbit(i) ) res += tr[i];return res;
}LL prefix_sum(int x)
{return (x + 1) * sum(tr1, x) - sum(tr2, x);
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]);for (int i = 1; i <= n; ++ i ) {LL b = a[i] - a[i - 1];add(tr1, i, b);add(tr2, i, b * i);}char op[2]; LL l, r, d;while (m -- ){scanf("%s%lld%lld", op, &l, &r);if (op[0] == 'C'){scanf("%lld", &d);add(tr1, l, d), add(tr1, r + 1, -d);add(tr2, l, l * d), add(tr2, r + 1, (r + 1) * -d);}else{printf("%lld\n", prefix_sum(r) - prefix_sum(l - 1));}}return 0;
}
debug:总是习惯LL用%d读取
244. 谜一样的牛
244. 谜一样的牛 - AcWing题库
从最后一个数开始往前推,若 a n a_n an为 k k k,说明前面有k头身高低于第n头牛的牛,此时 a n a_n an为所有身高中第 k + 1 k+1 k+1小的数,将该身高删除,因为每头牛的身高不同
若 a i a_i ai为 k k k,说明 a i a_i ai为剩下的身高中第 k + 1 k+1 k+1小的数
综上,需要实现两个操作:1. 删除某个身高 2. 计算身高中第 k k k小的数
除了平衡树,树状数组也能实现这两个操作
因为每头牛的身高不同,所以1~n中的每个数只能使用一次,将数组 b [ n ] b[n] b[n]的所有成员初始化成1,表示每个身高都没有使用过。一旦使用了某个身高,对应位置上的成员-1,由此可以实现第一个操作
用树状数组维护 b [ n ] b[n] b[n]数组的前缀和,如何计算数组中第k小的身高?若sum(x) = i说明小于等于x的身高中,有i个升高没有被使用
只要找到第一个满足sum(x) = k的x即可,此时的x就是剩下身高中第k小的身高,这个用二分可以实现
#include <iostream>
using namespace std;const int N = 1e5 + 10;
int n, a[N], tr[N], ans[N];int lowbit(int x)
{return x & (~x + 1);
}void add(int x, int c)
{for (int i = x; i <= n; i += lowbit(i) ) tr[i] += c;
}int sum(int x)
{int res = 0;for (int i = x; i; i -= lowbit(i)) res += tr[i];return res;
}int find(int x)
{int l = 1, r = n;while (l < r){int mid = l + r >> 1;if (sum(mid) >= x) r = mid;else l = mid + 1;}return l;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++ i ) {if (i > 1) scanf("%d", &a[i]);add(i, 1);}for (int i = n; i; -- i ) {ans[i] = find(a[i] + 1); // sum(mid) <= xadd(ans[i], -1);}for (int i = 1; i <= n; ++ i ) printf("%d\n", ans[i]);return 0;
}
相关文章:

第四章 No.1树状数组的原理与使用
文章目录 应用问题原理树状数组练习题241. 楼兰图腾242. 一个简单的整数问题243. 一个简单的整数问题2244. 谜一样的牛 线段树的反面:树状数组原理复杂,实现简单 应用问题 支持两个操作:快速求前缀和任意地修改某个数,时间复杂度…...

mysql(五)主从配置
目录 前言 一、MySQL Replication概述 二、MySQL复制类型 三、部署MySQL主从异步复制 总结 前言 为了实现MySQL的读写分离,可以使用MySQL官方提供的工具和技术,如MySQL Replication(复制)、MySQL Group Replication(组…...
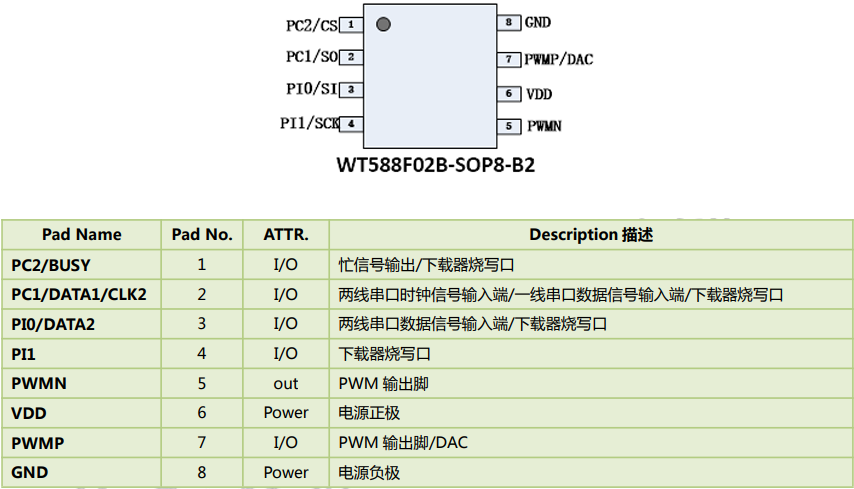
扫地机语音提示芯片,智能家居语音交互首选方案,WT588F02B-8S
智能家居已经成为现代家庭不可或缺的一部分,而语音交互技术正是智能家居的核心。在智能家居设备中,扫地机无疑是最受欢迎的产品之一。然而,要实现一个更智能的扫地机,需要一颗语音提示芯片,以提供高质量的语音交互体验…...
ChatGPT | 分割Word文字及表格,优化文本分析
知识库读取Word内容时,由于embedding切片操作,可能会出现表格被分割成多个切片的情况。这种切片方式可能导致“列名栏”和“内容栏”之间的Y轴关系链断裂,从而无法准确地确定每一列的数据对应关系,从而使得无法准确知道每一列的数…...

基于JavaSE的手机库存管理系统
1、项目背景 基于JavaSE完成如下需求: 功能需求: 1、查询库存量 2、可以修改库存中不同品牌手机的个数 3、退出系统 实现步骤: 1、把List当做库房 2、把手机存放在库房中 3、使用封装的方法区操作仓库中的手机 2、项目知识点 面向对象 集合…...
)
驱动开发 day4 (led灯组分块驱动)
//编译驱动(注意Makefile的编译到移植到开发板的内核) make archarm //清除编译生成文件 make clean //安装驱动 insmod mycdev.ko //卸载驱动 rmmod mycdev //编译fun.c 函数(用到交叉工具编译) arm-linux-gnueabihf-gcc fun.c head.h #ifndef __HEAD_H__ #define __HEAD_H__…...
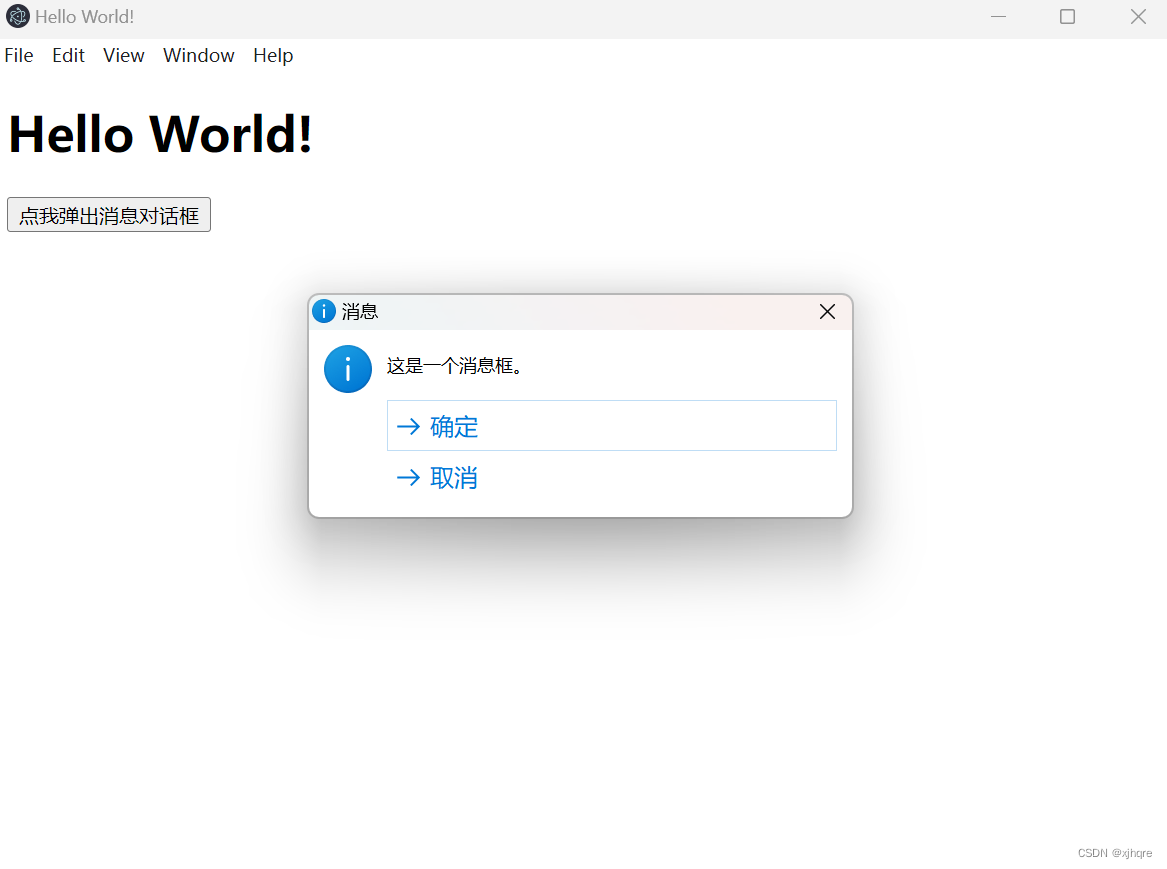
electron dialog.showMessageBox使用案例
electron 版本:25.3.1 index.html <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>Hello World!</title><meta http-equiv"Content-Security-Policy" content"script-src self unsa…...

代码随想录算法训练营第二十二天 | 读PDF复习环节2
读PDF复习环节2 本博客的内容只是做一个大概的记录,整个PDF看下来,内容上是不如代码随想录网站上的文章全面的,并且PDF中有些地方的描述,是很让我疑惑的,在困扰我很久后,无意间发现,其网站上的讲…...

TimescaleDB时序数据库初识
注:本文翻译自https://legacy-docs.timescale.com/v1.7/introduction TimescaleDB是一个开源时间序列数据库,针对快速摄取和复杂查询进行了优化。它说的是“完整的SQL”,因此像传统的关系数据库一样易于使用,并且以以前为NoSQL数…...

Numpy-聚合函数
NumPy 提供了很多统计函数,用于从数组中查找最小元素,最大元素,百分位标准差和方差等。 函数名说明np.sum()求和np.prod()所有元素相乘np.mean()平均值np.std()标准差np.var()方差np.median()中位数np.power()幂运算np.sqrt()开方np.min()最小…...
企业博客资讯如何高效运营起来?
运营一个高效的企业博客资讯需要综合考虑多个因素,包括内容策划、发布频率、优化推广、互动反馈等。下面将从这些方面介绍如何高效运营企业博客资讯。 如何高效运营企业博客资讯 内容策划 首先,需要制定一个明确的内容策略。确定博客的定位和目标受众…...

跟我学c++中级篇——模板的继承
一、继承 面向对象编程有三个特点:封装、继承和多态。其中继承在其中起着承上启下的作用。一般来说,继承现在和组合的应用比较难区分,出于各种场景和目的,往往各有千秋。但目前主流的观点,一般是如果没有特殊情况&…...
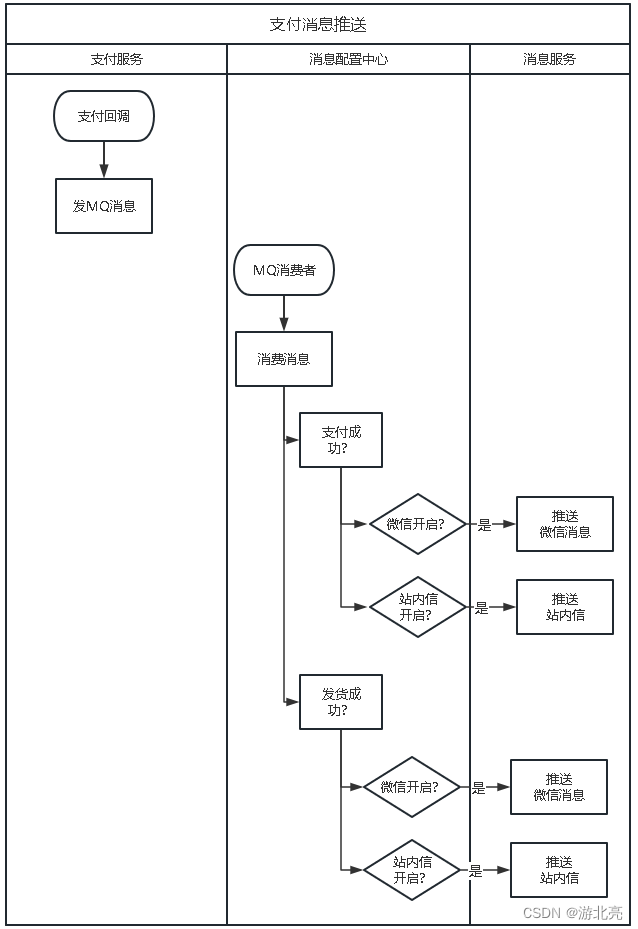
需求分析案例:消息配置中心
本文介绍了一个很常见的消息推送需求,在系统需要短信、微信、邮件之类的消息推送时,边界如何划分和如何设计技术方案。 1、需求 一个系统,一般会区分多个业务模块,并拆分成不同的业务系统,例如一个商城的架构如下&am…...

自动化测试——环境
一、搭建环境 1、安装Slenium pip install selenium 2、安装浏览器驱动-》查询浏览器版本-》下载对应版本驱动-》在path路径中配置(浏览器更新需要重新下载) pip install webdriver -helper(自动化)python3.9以上 pip install 安…...

短视频矩阵营销系统技术开发者开发笔记分享
一、开发短视频seo抖音矩阵系统需要遵循以下步骤: 1. 确定系统需求:根据客户的需求,确定系统的功能和特点,例如用户注册登录、视频上传、视频浏览、评论点赞等。 2. 设计系统架构:根据系统需求,设计系统的…...

vue2和vue3引用ueditor的区别
官方文档入口 UEditor Docs vue2使用方式 UE.vue组件 <template><div><script id"editor" type"text/plain"></script><Upload v-if"isupload" :config"{total:9}" :isupload"isupload" ret…...
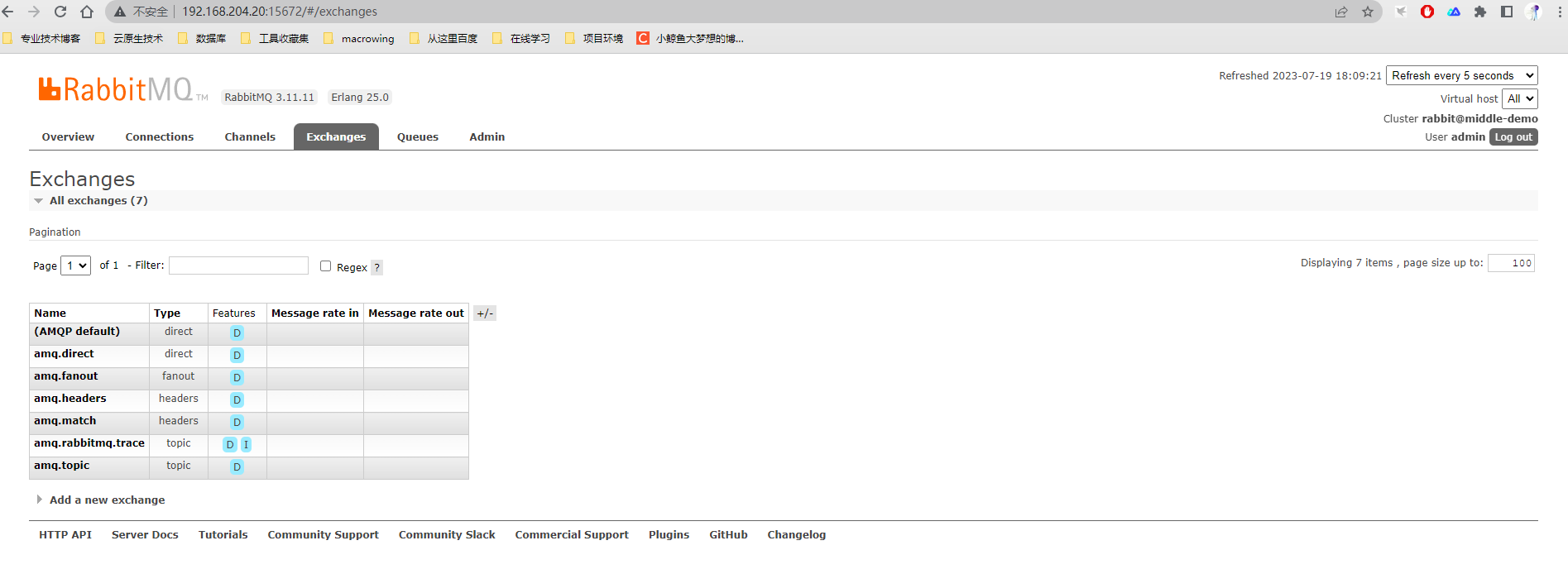
【每日运维】RockyLinux8非容器化安装Mysql、Redis、RabitMQ单机环境
系统版本:RockyLinux 8.6 安装方式:非容器化单机部署 安装版本:mysql 8.0.32 redis 6.2.11 rabbitmq 3.11.11 elasticsearch 6.7.1 前置条件:时间同步、关闭selinux、主机名、主机解析host 环境说明:PC电脑VMware Work…...
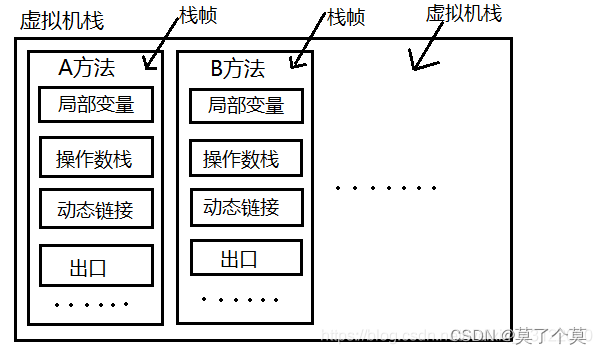
第一次后端复习整理(JVM、Redis、反射)
1. JVM 文章仅为自身笔记 详情查看一篇文章掌握整个JVM,JVM超详细解析!!! 1.1 什么是JVM jvm是Java虚拟机 1.2 Java文件的编译过程 程序员编写代码形成.java文件经过javac编译成.class文件再通过JVM的类加载器进入运行时数据…...
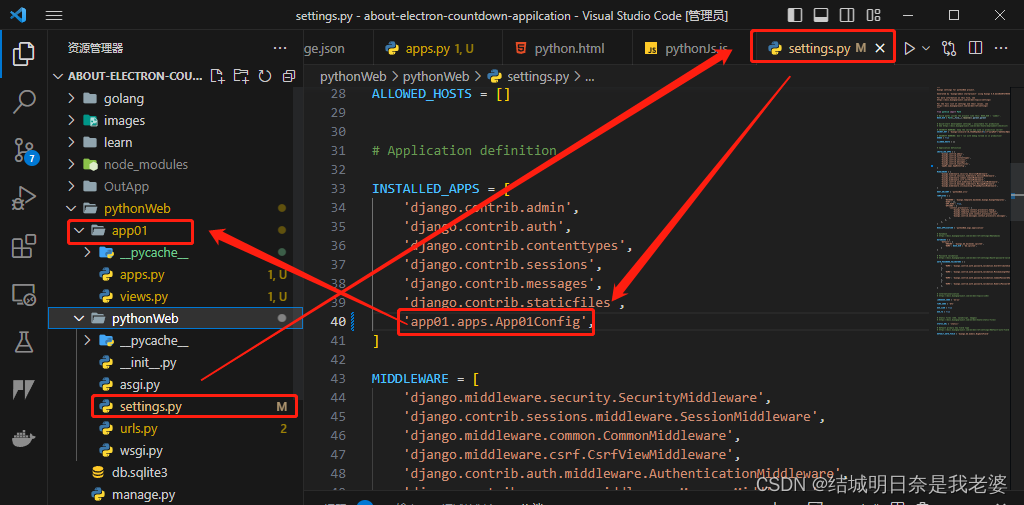
python的web学习(一)-初识django
文章目录 软件创建项目默认项目文件说明App的概念(应用)apps.py编写URL和视图函数对应关系【urls.py】编写视图函数【views.py】启动服务 软件 python下载 django下载 创建项目 django-admin startproject 文件名默认项目文件说明 项目名 manage.py(项目管理,启…...
JavaWeb+jsp+Tomcat的叮当书城项目
点击以下链接获取源码: https://download.csdn.net/download/qq_64505944/88123111?spm1001.2014.3001.5503 技术:ssm jsp JDK1.8 MySQL5.7 Tomcat8.3 源码数据库课程设计 功能:管理员与普通用户和超级管理员三个角色,管理员可…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
